2019.4做题记录

　　还没写完就退役了，所以发出来吧。如果哪天想起来再把没写的题解补上。

　　最近才发现，把题解更到旧文章里，不仅别人看着麻烦，就连自己也找不到...

　　但是！如果根本不更题解，就不存在找不到的问题了！

　　好吧...上述内容纯属娱乐，下面还是开始写做题记录。其实题目有点歧义，并不是四月的做题记录，主要指的还是省选后的题目，不过如果有空也会把省选前的题目写一写；

　　发现这两个符号“「」”非常漂亮，所以每道题目都打上了；

4.8：

　　「异或粽子」：https://www.lydsy.com/JudgeOnline/problem.php?id=5495

　　十二省联考D1T1.这题长得跟“超级钢琴”几乎一模一样，所以也没多想，直接套用了那个做法。怎么找区间异或第 $k$ 大呢？可持久化Trie树就好啦。

　　刚刚在bzoj上查这题，只输入了“异或”两个字，跳出来一个题叫“异或之”，好奇地点进去看了看，跟这题一模一样！一模一样！省选就是这么出题的吗？

  1 # include <cstdio>
  2 # include <iostream>
  3 # include <queue>
  4 # define R register int
  5 # define ll long long
  6 # define pac(a,b) make_pair(a,b)
  7  
  8 using namespace std;
  9  
 10 const int maxn=500005;
 11 int n,k,cnt,rt[maxn];
 12 ll a[maxn],ans,x;
 13 struct node { int pos,k; }s[maxn];
 14 struct tn { int l,r,siz; }t[maxn*40];
 15 typedef pair <ll,int> pii;
 16 priority_queue <pii,vector<pii>,less<pii> > q;
 17 pii tt;
 18  
 19 void ins (int &n,int las,ll x,int w)
 20 {
 21     if(!n) n=++cnt;
 22     if(w<0) { t[n].siz=t[las].siz+1; return; }
 23     if(x&(1LL<<w))
 24     {
 25         t[n].l=t[las].l;
 26         ins(t[n].r,t[las].r,x,w-1);
 27     }
 28     else
 29     {
 30         t[n].r=t[las].r;
 31         ins(t[n].l,t[las].l,x,w-1);
 32     }
 33     t[n].siz=t[ t[n].l ].siz+t[ t[n].r ].siz;
 34 }
 35  
 36 ll ask (int a,int b,ll x,int k)
 37 {
 38     ll ans=0;
 39     int c,s;
 40     for (R i=35;i>=0;--i)
 41     {
 42         if(x&(1LL<<i)) c=0; else c=1;
 43         if(c==0)
 44         {
 45             s=t[ t[b].l ].siz-t[ t[a].l ].siz;
 46             if(s>=k)
 47             {
 48                 ans=ans*2LL+1;
 49                 a=t[a].l; b=t[b].l;
 50             }
 51             else
 52             {
 53                 k-=s;
 54                 ans=ans*2LL;
 55                 a=t[a].r; b=t[b].r;
 56             }
 57         }
 58         else
 59         {
 60             s=t[ t[b].r ].siz-t[ t[a].r ].siz;
 61             if(s>=k)
 62             {
 63                 ans=ans*2LL+1;
 64                 a=t[a].r; b=t[b].r;
 65             }
 66             else
 67             {
 68                 k-=s;
 69                 ans=ans*2LL;
 70                 a=t[a].l; b=t[b].l;
 71             }
 72         }
 73     }
 74     return ans;
 75 }
 76  
 77 ll read()
 78 {
 79     ll x=0;
 80     char c=getchar();
 81     while (!isdigit(c)) c=getchar();
 82     while (isdigit(c)) x=x*10LL+(c^48),c=getchar();
 83     return x;
 84 }
 85  
 86 int main()
 87 {
 88     scanf("%d%d",&n,&k);
 89     for (R i=1;i<=n;++i) a[i]=read(),a[i]^=a[i-1];
 90     for (R i=1;i<=n;++i)
 91         ins(rt[i],rt[i-1],a[i],35);
 92     for (R i=0;i<n;++i)
 93     {
 94         s[i].pos=i; s[i].k=1;
 95         x=ask(rt[i],rt[n],a[i],1);
 96         q.push(pac(x,i));
 97     }
 98     for (R i=1;i<=k;++i)
 99     {
100         tt=q.top(); q.pop();
101         ans+=tt.first;
102         int id=tt.second;
103         if(n-s[id].pos<=s[id].k) continue;
104         s[id].k++;
105         x=ask(rt[s[id].pos],rt[n],a[s[id].pos],s[id].k);
106         q.push(pac(x,id));
107     }
108     printf("%lld",ans);
109     return 0;
110 }

异或粽子

　　「幸运数字」：https://www.lydsy.com/JudgeOnline/problem.php?id=1853

　　题意概述：定义幸运数字为每个数位要么是6要么是8的数字，近似幸运数字为幸运数字的倍数，求区间 $[A,B]$ 中有多少个近似幸运数字。$a,b<=10^{10}$

　　乍一看好像没法下手，但是可以发现给定区间内幸运数字不是很多，搜索一下把它们找出来。又发现如果 $a|b,b|c$ ，那么有 $a|c$ ，所以对于有倍数关系的两个幸运数字，只需要保留那个较小的。这样处理后，$10^{10}$ 中留下的数字就不到一千个了。现在只需要把每个数的倍数个数求出来了。直接对于每个数算倍数个数还是不对，需要容斥...1000能容斥...?还真的行，因为不需要很多数，它们的最小公倍数就会超过上界，将数按照大小排序(让最小公倍数尽快越界，加快速度)，dfs即可.复杂度？O(能过).

 1 # include <cstdio>
 2 # include <iostream>
 3 # include <algorithm>
 4 # include <vector>
 5 # define R register int
 6 # define ll long long
 7 # define ULL unsigned long long
 8  
 9 using namespace std;
10  
11 int h;
12 int vis[5000];
13 ULL s[5000];
14 ULL a,b;
15 ll ans;
16  
17 void dfs1 (ULL x)
18 {
19     if(x>b) return;
20     if(x) s[++h]=x;
21     dfs1(x*10+6);
22     dfs1(x*10+8);
23 }
24  
25 ll cal (ll x)
26 {
27     return b/x-(a-1)/x;
28 }
29  
30 ll gcd (ll a,ll b) { return b?gcd(b,a%b):a; }
31  
32 void dfs (ULL x,int cnt,int no)
33 {
34     if(x>b) return;
35     if(no==h+1)
36     {
37         if(!cnt) return;
38         if(cnt&1) ans+=cal(x);
39         else ans-=cal(x);
40         return;
41     }
42     dfs(x,cnt,no+1);
43     dfs(x/gcd(x,s[no])*s[no],cnt+1,no+1);
44 }
45  
46 bool cmp (ll a,ll b) { return a>b; }
47  
48 int main()
49 {
50     cin>>a>>b;
51     dfs1(0);
52     sort(s+1,s+1+h,cmp);
53     for (R i=1;i<=h;++i)
54         for (R j=i+1;j<=h;++j)
55             if(s[i]%s[j]==0) vis[i]=1;
56     for (R i=1;i<=h;++i) if(vis[i]) s[i]=0;
57     sort(s+1,s+1+h,cmp);
58     while(s[h]==0) h--;
59     dfs(1,0,1);
60     printf("%lld",ans);
61     return 0;
62 }

幸运数字

　　「春节十二响」：https://www.lydsy.com/JudgeOnline/problem.php?id=5499

　　题意概述：将一棵树分为若干块，同一块之间的点不能存在祖孙关系，定义每一块的权值为块内点权值的最大值，求总权值的最小值。$n<=2\times 10^5$

　　考场傻掉了，完全没思路，最后写了一个状压dp+链的部分分。首先对于链的部分分，可以发现两条支链必然是最大配最大，次大配次大这样，合并以后就变成了一条链，所以对于多条支链的情况，只需一一合并，使用启发式合并，复杂度 $nlogn$.

 1 // luogu-judger-enable-o2
 2 # include <cstdio>
 3 # include <iostream>
 4 # include <queue>
 5 # define R register int
 6 # define ll long long
 7 
 8 using namespace std;
 9 
10 const int maxn=200005;
11 int h,firs[maxn],n,v[maxn],dep[maxn],vc[maxn],tp,x,no[maxn];
12 ll ans=0;
13 struct edge { int too,nex; }g[maxn<<1];
14 priority_queue <int,vector<int>,less<int> >q[maxn];
15 
16 void dfs (int x)
17 {
18     int j,cnt=0,y;
19     no[x]=x;
20     for (R i=firs[x];i;i=g[i].nex)
21     {
22         j=g[i].too;
23         if(dep[j]) continue;
24         dep[j]=1;
25         dfs(j);
26         j=no[j];
27         cnt++;
28         if(cnt==1)
29             no[x]=j;
30         else
31         {
32             y=no[x];
33             int siz1=q[y].size(),siz2=q[j].size();
34             tp=0;
35             for (R i=1;i<=min(siz1,siz2);++i)
36             {
37                 vc[++tp]=max(q[y].top(),q[j].top());
38                 q[y].pop(); q[j].pop();
39             }
40             if(siz1>=siz2)
41                 for (R i=1;i<=tp;++i) q[y].push(vc[i]);
42             else
43             {
44                 for (R i=1;i<=tp;++i) q[j].push(vc[i]);
45                 no[x]=j;
46             }
47         }
48     }
49     y=no[x];
50     q[y].push(v[x]);
51 }
52 
53 void add (int x,int y)
54 {
55     g[++h].nex=firs[x];
56     g[h].too=y;
57     firs[x]=h;
58 }
59 
60 int read()
61 {
62     R x=0;
63     char c=getchar();
64     while (!isdigit(c)) c=getchar();
65     while (isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar();
66     return x;
67 }
68 
69 int main()
70 {
71     scanf("%d",&n);
72     for (R i=1;i<=n;++i) v[i]=read();
73     for (R i=2;i<=n;++i)
74     {
75         x=read();
76         add(i,x); add(x,i);
77     }
78     dep[1]=1;
79     dfs(1);
80     while(q[ no[1] ].size()) ans+=q[ no[1] ].top(),q[ no[1] ].pop();
81     printf("%lld",ans);
82     return 0;
83 }

春节十二响

4.9：

　　「字符串问题」：https://www.lydsy.com/JudgeOnline/problem.php?id=5496

　　题意概述：给定一个大字符串，并从中截取一些A串，一些B串，给定一些支配关系（A支配B)，选出一些A（可重）拼到一起，使得每个串后面拼的那个串的某个前缀是它支配的串（好绕）。

　　考场成功写挂拓扑排序，过不了大样例，只好挂上暴力，痛失50分。

　　其实这题不算特别难的。首先对于总串倒序建立SAM，并使用倍增为每个串定位。如果一个A支配一个B，那么可以拼在它后面的A就一定在那个B的子树内，将SAM上的边实体化，并连接支配边，跑拓扑排序求权值最大的路径。注意：权值必须放到支配边上，而不是点上，因为在SAM上走来走去不能增加答案。这样做就可以得到80分了。发现刚刚讨论的前提建立在所有A都比B长上，如果一个 $A$ 一个 $B$ 定位到了同一个 $SAM$ 的节点上，且 $B$ 比 $A$ 长，这样做就挂了，所以出现这种情况时考虑拆点。如果一 $A$ 一 $B$ 一样长，那么应该把 $B$ 放到前面。然而对于AB分类讨论有点复杂，不如将相同的串映射到一个相同的新ID上，我就是这么写的。[本题略微卡常，清空数组时请用多少清多少]

  1 // luogu-judger-enable-o2
  2 # include <cstdio>
  3 # include <iostream>
  4 # include <cstring>
  5 # include <queue>
  6 # include <vector>
  7 # include <algorithm>
  8 # include <map>
  9 # include <set>
 10 # define ULL unsigned long long
 11 # define R register int
 12 # define ll long long
 13 # define pac(a,b) make_pair(a,b)
 14 
 15 using namespace std;
 16 
 17 const int maxn=400005;
 18 int T,n,na,nb,m;
 19 int la[maxn],lb[maxn],ra[maxn],rb[maxn],dfn;
 20 int x[maxn],y[maxn],lg[maxn],dep[maxn],lid;
 21 int vis[maxn];
 22 char s[maxn];
 23 int h=0,firs[maxn<<1],las=0,cnt=0,t,yhm;
 24 int p[maxn],ch[maxn][26],len[maxn],en[maxn],sta[maxn],in_sta[maxn],tp;
 25 int posa[maxn],posb[maxn],f[maxn][22];
 26 int ida[maxn],idb[maxn];
 27 int son[maxn],bro[maxn];
 28 int beg[maxn],ed[maxn];
 29 struct edge { int too,nex,co; }g[maxn*10];
 30 int r[maxn<<1],il[maxn];
 31 ll dp[maxn<<1];
 32 queue <int> q;
 33 vector <int> v[maxn];
 34 typedef pair <int,int> pii;
 35 map <pii,int> mp;
 36 //多组数据！！！ 
 37 
 38 int ins (int c)
 39 {
 40     int f=las,no=++cnt; las=no;
 41     len[no]=len[f]+1;
 42     while(f&&!ch[f][c]) ch[f][c]=no,f=p[f];
 43     if(!f) { p[no]=1; return no; }
 44     int x=ch[f][c],q;
 45     if(len[x]==len[f]+1) { p[no]=x; return no; }
 46     q=++cnt; len[q]=len[f]+1;
 47     p[q]=p[x]; p[x]=p[no]=q;
 48     for (R i=0;i<26;++i) ch[q][i]=ch[x][i];
 49     while(f&&ch[f][c]==x) ch[f][c]=q,f=p[f];
 50     return no;
 51 }
 52 
 53 void add (int x,int y,int z)
 54 {
 55     g[++h].nex=firs[x];
 56     firs[x]=h;
 57     g[h].too=y;
 58     g[h].co=z;
 59 }
 60 
 61 void dfs (int x)
 62 {
 63     for (R i=son[x];i;i=bro[i])
 64     {
 65         f[i][0]=x;
 66         dep[i]=dep[x]+1;
 67         for (R k=1;k<=lg[ dep[i] ];++k) f[i][k]=f[ f[i][k-1] ][k-1];
 68         dfs(i);
 69     }
 70 }
 71 
 72 bool cmp (int a,int b) { return il[a]<il[b]; }
 73 
 74 void redfs (int x)
 75 {
 76     int siz=v[x].size();
 77     if(siz)
 78     {
 79         sort(v[x].begin(),v[x].end(),cmp);
 80         beg[x]=v[x][0]; ed[x]=v[x][siz-1];
 81         for (R i=0;i<siz-1;++i)
 82             add(v[x][i],v[x][i+1],0);
 83     }
 84     else
 85         beg[x]=ed[x]=++lid;
 86     for (R i=son[x];i;i=bro[i])
 87     {
 88         redfs(i);
 89         add(ed[x],beg[i],0);
 90     }    
 91 }
 92 
 93 int find (int x,int l)
 94 {
 95     for (R i=lg[ dep[x] ];i>=0;--i)
 96         if(len[ f[x][i] ]>=l) x=f[x][i];
 97     return x;
 98 }
 99 
100 ll DP (int t)
101 {
102     ll ans=0; int num=0;
103     for (R i=1;i<=t;++i)
104         for (R j=firs[i];j;j=g[j].nex)
105             r[ g[j].too ]++;
106     for (R i=1;i<=t;++i) if(!r[i]) q.push(i),num++;
107     int beg,j;
108     while(q.size())
109     {
110         beg=q.front(); q.pop();
111         for (R i=firs[beg];i;i=g[i].nex)
112         {
113             j=g[i].too;
114             dp[j]=max(dp[j],dp[beg]+g[i].co);
115             r[j]--;
116             if(!r[j]) q.push(j),num++;            
117         }
118     }
119     for (R i=1;i<=t;++i) ans=max(ans,dp[i]);
120     if(num<t) return -1;
121     return ans;
122 }
123 
124 int read()
125 {
126     R x=0;
127     char c=getchar();
128     while (!isdigit(c)) c=getchar();
129     while (isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar();
130     return x;
131 }
132 
133 void clr()
134 {
135     for (R i=1;i<=cnt;++i)
136     {
137         memset(ch[i],0,sizeof(ch[i]));
138         p[i]=0; len[i]=0;
139         for (R j=0;j<=20&&f[i][j];++j) f[i][j]=0;    
140         v[i].clear();
141     }
142     h=0;
143     memset(son,0,sizeof(int)*(cnt+2));
144     memset(bro,0,sizeof(int)*(cnt+2));
145     memset(firs,0,sizeof(int)*(lid+2));
146     memset(r,0,sizeof(int)*(lid+2));
147     memset(vis,0,sizeof(vis));
148     memset(dp,0,sizeof(dp));
149     cnt=las=1; lid=0;
150     mp.clear();
151 }
152 
153 int main()
154 {
155     T=read();
156     while(T--)
157     {
158         scanf("%s",s+1); n=strlen(s+1);
159         clr();
160         for (R i=n;i>=1;--i)
161             en[i]=ins(s[i]-'a');
162         for (R i=1;i<=cnt;++i)
163             bro[i]=son[ p[i] ],son[ p[i] ]=i;
164         dep[1]=1;
165         for (R i=2;i<=cnt;++i) lg[i]=lg[i>>1]+1;
166         dfs(1);
167         na=read();
168         for (R i=1;i<=na;++i)
169         {
170             la[i]=read(),ra[i]=read();
171             int len=ra[i]-la[i]+1;
172             posa[i]=find(en[ la[i] ],len);
173             int x=mp[pac(posa[i],len)];
174             if(!x) x=mp[pac(posa[i],len)]=++lid;
175             ida[i]=x;
176             il[x]=len;
177         }
178         nb=read();
179         for (R i=1;i<=nb;++i)
180         {
181             lb[i]=read(),rb[i]=read();
182             int len=rb[i]-lb[i]+1;
183             posb[i]=find(en[ lb[i] ],len);
184             int x=mp[pac(posb[i],len)];
185             if(!x) x=mp[pac(posb[i],len)]=++lid;
186             idb[i]=x;
187             il[x]=len;
188         }
189         m=read();
190         for (R i=1;i<=m;++i)
191             x[i]=read(),y[i]=read();
192         for (R i=1;i<=na;++i)
193         {
194             if(vis[ ida[i] ]) continue;
195             vis[ ida[i] ]=1;
196             v[ posa[i] ].push_back(ida[i]);
197         }
198         for (R i=1;i<=nb;++i)
199         {
200             if(vis[ idb[i] ]) continue;
201             vis[ idb[i] ]=1;
202             v[ posb[i] ].push_back(idb[i]);
203         }
204         redfs(1);
205         for (R i=1;i<=m;++i)
206             add(ida[ x[i] ],idb[ y[i] ],ra[ x[i] ]-la[ x[i] ]+1);
207         t=++lid;
208         for (R i=1;i<=na;++i)
209             add(ida[i],t,ra[i]-la[i]+1);
210         printf("%lld\n",DP(lid));
211     }
212     return 0;
213 }

字符串问题

　　「Dominant Indices」:https://www.luogu.org/problemnew/show/CF1009F

　　题意概述：给定一棵树，求每个点的子树中，哪个深度的点最多。$n<=10^6$

　　可以想到一个比较简单的做法：$f[i][j]$ 表示以 $i$ 为根的子树里,有多少个点的深度为 $j$.然而这样显然过不了。

　　其实这是一道长链剖分的模板题。注意到刚刚的转移只与深度有关，所以首先求出每个点的子树里最深的点到它的距离。利用指针的技巧 $O(1)$ 地继承最长儿子的信息，对于具体实现来说，应该是长儿子直接使用父亲的dp数组进行计算。$f[ son[i] ]=f[ i ]+1$。对于轻儿子进行暴力合并，发现每个点只会被暴力合并一次，所以复杂度竟然是 $O(n)$.

 1 # include <cstdio>
 2 # include <iostream>
 3 # define R register int
 4 
 5 using namespace std;
 6 
 7 const int maxn=1000006;
 8 int n,x,y,h,firs[maxn],dep[maxn],len[maxn],son[maxn];
 9 struct edge { int too,nex; }g[maxn<<1];
10 int *f[maxn],ans[maxn],tp[maxn],*id=tp;
11 
12 int read()
13 {
14     R x=0;
15     char c=getchar();
16     while (!isdigit(c)) c=getchar();
17     while (isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar();
18     return x;
19 }
20 
21 void add (int x,int y)
22 {
23     g[++h].nex=firs[x];
24     firs[x]=h;
25     g[h].too=y;
26 }
27 
28 void dfs (int x)
29 {
30     int j,maxs=-1;
31     for (R i=firs[x];i;i=g[i].nex)
32     {
33         j=g[i].too;
34         if(dep[j]) continue;
35         dep[j]=dep[x]+1;
36         dfs(j);
37         if(len[j]>=maxs) maxs=len[j],son[x]=j;
38     }
39     len[x]=len[ son[x] ]+1;
40 }
41 
42 void dp (int x)
43 {
44     int j;
45     f[x][0]=1;
46     if(son[x]) f[ son[x] ]=f[x]+1,dp(son[x]),ans[x]=ans[ son[x] ]+1;
47     for (R i=firs[x];i;i=g[i].nex)
48     {
49         j=g[i].too;
50         if(dep[j]<dep[x]||j==son[x]) continue;
51         f[j]=id; id+=len[j];
52         dp(j);
53         for (R k=1;k<=len[j];++k)
54         {
55             f[x][k]+=f[j][k-1];
56             if((k<ans[x]&&f[x][k]>=f[x][ ans[x] ])||(k>ans[x]&&f[x][k]>f[x][ ans[x] ]))
57                 ans[x]=k;
58         }
59     }
60     if(f[x][ ans[x] ]==1) ans[x]=0;
61 }
62 
63 int main()
64 {
65     scanf("%d",&n);
66     for (R i=1;i<n;++i)
67     {
68         scanf("%d%d",&x,&y);
69         add(x,y); add(y,x);
70     }
71     dep[1]=1;
72     dfs(1);
73     f[1]=id; id+=len[1];
74     dp(1);
75     for (R i=1;i<=n;++i) printf("%d\n",ans[i]);
76     return 0;
77 }

Dominant Indices

　　「分析矿洞」：https://www.luogu.org/problemnew/show/U18201

　　题意概述：矿洞是一个 $n\times n$的点阵，一个人现在站在 $(0,0)$，向第一象限看去，定义每个点的价值为 $(\frac{x+y}{x_0+y_0})^2$，这里的 $(x_0,y_0)$ 是指从 $(0,0)$ 看向这里的路径上穿过的第一个点的坐标，而整个矿洞的价值即为 $\sum_{i=1}^n\sum_{j=1}^n\varphi(V_{i,j})$，求总价值。$n<=10^{10}$

　　首先直觉告诉我们，第一个穿过的点的坐标应该是：$(\frac{x}{(x,y)},\frac{y}{(x,y)})$，因为这个坐标是原坐标按比例缩小所能缩到的最小的一个点，于是来化式子吧。

　　$\begin{align*} V_{i,j}&=(\frac{x+y}{\frac{x}{(x,y)}+\frac{y}{(x,y)}})^2\\ \\&=(\frac{x+y}{\frac{x+y}{(x,y)}})^2\\ \\&=(x,y)^2 \end{align*} $

　　$\begin{align*} S&=\sum\limits_{i=1}^n\sum\limits_{j=1}^n\varphi((i,j)^2)\\ \\ &=\sum\limits_{i=1}^n\sum\limits_{j=1}^n\varphi((i,j))(i,j) \\ \\ &=\sum\limits_{d=1}^n\varphi(d) d\sum\limits_{i=1}^n\sum\limits_{j=1}^n[(i,j)=d]\\ \\ &=\sum\limits_{d=1}^n\varphi(d) d\sum\limits_{i=1}^{\frac{n}{d}}\sum\limits_{j=1}^{\frac{n}{d}}[(i,j)=1]\\ \\ &=\sum\limits_{d=1}^n\varphi(d) d\sum\limits_{i=1}^{\frac{n}{d}}(2\times \varphi(i)-1)\\ \\ &=\sum\limits_{d=1}^n(2\times S(\frac{n}{d})-1)\varphi(d) d\end{align*}$

　　那么，前面除法分块+杜教筛，后面杜教筛即可。杜教筛 $\varphi$ 之前已经写过，所以现在主要看看后半部分，尝试一下卷个 $id$ 吧?　　

　　$H(n)=\sum\limits_{i=1}^n\sum\limits_{d|i}\varphi(d)d\frac{i}{d}=\sum\limits_{i=1}^n\sum\limits_{d|i}\varphi(d)i=\sum\limits_{i=1}^ni\sum\limits_{d|i}\varphi(d)=\sum\limits_{i=1}^ni^2$

　　这么做就成功啦，两个杜教筛是并列的，所以很快。（据说如果真的套在一起也还是很快？)

 1 // luogu-judger-enable-o2
 2 # include <cstdio>
 3 # include <iostream>
 4 # include <tr1/unordered_map>
 5 # define R register int
 6 # define ll long long
 7 
 8 using namespace std;
 9 
10 const int mod=1000000007;
11 const int maxn=5000006;
12 const ll inv2=500000004;
13 const ll inv6=166666668;
14 int h,vis[maxn],N;
15 ll pri[maxn],phi[maxn],s[maxn],sphi[maxn];
16 ll n,ans;
17 tr1::unordered_map <ll,ll> m1;
18 tr1::unordered_map <ll,ll> m2;
19 
20 void init (int n)
21 {    
22     phi[1]=1;
23     for (R i=2;i<=n;++i)
24     {
25         if(!vis[i]) pri[++h]=i,phi[i]=i-1;
26         for (R j=1;j<=h&&i*pri[j]<=n;++j)
27         {
28             vis[ i*pri[j] ]=1;
29             if(i%pri[j]==0)
30             {
31                 phi[ i*pri[j] ]=phi[i]*pri[j]%mod;
32                 break;
33             }
34             phi[ i*pri[j] ]=phi[i]*phi[ pri[j] ]%mod;
35         }
36     }
37     for (R i=1;i<=n;++i) s[i]=(s[i-1]+phi[i])%mod;
38     for (R i=1;i<=n;++i) sphi[i]=(sphi[i-1]+phi[i]*i%mod)%mod;
39 }
40 
41 ll s1 (ll x) { x%=mod; return x*(x+1)%mod*inv2%mod; }
42 ll s2 (ll x) { x%=mod; return x*(x+1)%mod*(2*x%mod+1)%mod*inv6%mod; }
43 
44 ll ask1 (ll x)
45 {
46     if(x<=N) return s[x];
47     if(m1[x]) return m1[x];
48     ll ans=s1(x),l=2,r;
49     while(l<=x)
50     {
51         r=x/(x/l);
52         ans=(ans-ask1(x/l)*(r-l+1)%mod+mod)%mod;
53         l=r+1;
54     }
55     return m1[x]=ans;
56 }
57 
58 ll ask2 (ll x)
59 {
60     if(x<=N) return sphi[x];
61     if(m2[x]) return m2[x];
62     ll ans=s2(x),l=2,r;
63     while(l<=x)
64     {
65         r=x/(x/l);
66         ans=(ans-ask2(x/l)*(s1(r)-s1(l-1)+mod)%mod+mod)%mod;
67         l=r+1;
68     }
69     return m2[x]=ans;
70 }
71 
72 int main()
73 {
74     scanf("%lld",&n);
75     N=min(n,5000000LL);
76     init(N);
77     ll l=1,r;
78     while(l<=n)
79     {
80         r=n/(n/l);
81         ans=(ans+(2LL*ask1(n/l)-1+mod)%mod*((ask2(r)-ask2(l-1))%mod+mod)%mod+mod)%mod;
82         l=r+1;
83     }
84     printf("%lld",ans);
85     return 0;
86 }

分析矿洞

4.10：

　　「Pollard-Rho」:https://www.luogu.org/problemnew/show/P4718

　　做法见单独的总结，此处只有代码。

  1 // luogu-judger-enable-o2
  2 # include <cstdio>
  3 # include <iostream>
  4 # include <cstdlib>
  5 # include <ctime>
  6 # define R register int
  7 # define ll long long
  8 # define ull unsigned long long
  9 
 10 using namespace std;
 11 
 12 const int pri[]={0,2,7,61,709,2003};
 13 int cnt=5;
 14 int cas;
 15 ll x,ans;
 16 
 17 ll mul (ull x,ull y,ll p)
 18 {
 19     return (x*y-(ull)((long double)x/p*y)*p+p)%p;
 20 }
 21 
 22 ll qui (ll a,ll b,ll p)
 23 {
 24     ll s=1; a%=p;
 25     while(b)
 26     {
 27         if(b&1) s=mul(s,a,p);
 28         a=mul(a,a,p);
 29         b>>=1;
 30     }
 31     return s;
 32 }
 33 
 34 bool check (ll x,ll p,ll y)
 35 {
 36     ll t=qui(x,y,p);
 37     if(t!=1&&t!=p-1) return false;
 38     if(t==p-1) return true;
 39     if(t==1&&(y%2)) return true;
 40     return check(x,p,y/2);
 41 }
 42 
 43 
 44 bool Miller_Rabin (ll x)
 45 {
 46     if(x<=1) return false;
 47     if(x==2||x==7||x==61||x==709) return true;
 48     if(check(2,x,x-1)&&check(7,x,x-1)&&check(61,x,x-1)&&check(709,x,x-1)) return true;
 49     return false;
 50 }
 51 
 52 ll gcd (ll a,ll b) { return b?gcd(b,a%b):a; }
 53 
 54 void Pollard_Rho (ll n)
 55 {
 56     if(n<=ans) return;
 57     if(n==1) return;
 58     if(Miller_Rabin(n)) { ans=max(ans,n); return; }
 59     if(n%2==0)
 60     {
 61         while(n%2==0) n/=2;
 62         ans=max(ans,2LL);
 63         Pollard_Rho(n);
 64         return;
 65     }
 66     ll x,y,c,d,z=1; int i,k;
 67     while(1)
 68     {
 69         x=y=rand()%n;
 70         c=rand()%n;
 71         z=1; i=0,k=1;
 72         while(1)
 73         {
 74             x=(mul(x,x,n)+c)%n;
 75             i++;
 76             z=mul(z,max(x-y,y-x),n);
 77             if(x==y||!z) break;
 78             if(i%100==0||i==k)
 79             {
 80                 d=gcd(z,n);
 81                 if(d!=1&&d!=n)
 82                 {
 83                     while(n%d==0) n/=d;
 84                     Pollard_Rho(d);
 85                     Pollard_Rho(n);
 86                     return;
 87                 }
 88                 if(i==k) y=x,k<<=1;
 89             }
 90         }
 91     }
 92 }
 93 
 94 int main()
 95 {
 96     srand(time(0));
 97     scanf("%d",&cas);
 98     for (R i=1;i<=cas;++i)
 99     {
100         scanf("%lld",&x);
101         if(x==1) { puts("0"); continue; }
102         ans=1;
103         Pollard_Rho(x);
104         if(ans==x) puts("Prime");
105         else printf("%lld\n",ans);
106     }
107     return 0;
108 }

Pollard-Rho

　　「Rabin-Miller算法」：https://www.lydsy.com/JudgeOnline/problem.php?id=3667

　　我能说“同上”吗...

　　「欧拉函数」：https://www.lydsy.com/JudgeOnline/problem.php?id=4802

　　题意概述：求 $\varphi(n)$. $n<=10^{18}$

　　欧拉函数有这么一个定义式：$\varphi(n)=n\times \prod(1-\frac{1}{p_i})$

　　所以Pollard-Rho分解质因数，然后套用定义式即可。

  1 # include <cstdio>
  2 # include <iostream>
  3 # include <cstdlib>
  4 # include <ctime>
  5 # include <algorithm>
  6 # define R register int
  7 # define ll long long
  8 # define ull unsigned long long
  9  
 10 using namespace std;
 11  
 12 const int pri[]={0,2,3,7,61,709,24251};
 13 const int maxn=1000;
 14 ll n;
 15 ll a[maxn];
 16 int h;
 17  
 18 ll mul (ull a,ull b,ull p) { return (a*b-(ull)((long double)a/p*b)*p+p)%p; }
 19  
 20 ll qui (ll a,ll b,ll p)
 21 {
 22     ll s=1;
 23     while (b)
 24     {
 25         if(b&1) s=mul(s,a,p);
 26         a=mul(a,a,p);
 27         b>>=1;
 28     }
 29     return s;
 30 }
 31  
 32 bool check (ll x,ll p,ll y)
 33 {
 34     ll t=qui(x,y,p);
 35     if(t!=1&&t!=p-1) return false;
 36     if(t==p-1) return true;
 37     if(t==1&&(y&1)) return true;
 38     return check(x,p,y/2);
 39 }
 40  
 41 bool Miller_Rabin (ll n)
 42 {
 43     if(n<=1) return false;
 44     for (R i=1;i<=6;++i) if(n==pri[i]) return true;
 45     for (R i=1;i<=6;++i) if(!check(pri[i],n,n-1)) return false;
 46     return true;
 47 }
 48  
 49 ll gcd (ll a,ll b) { return b?gcd(b,a%b):a; }
 50  
 51 void Pollard_Rho (ll n)
 52 {
 53     if(n<=1) return;
 54     if(Miller_Rabin(n)) { a[++h]=n; return; }
 55     if(n%2==0)
 56     {
 57         while(n%2==0) n/=2;
 58         a[++h]=2;
 59         Pollard_Rho(n);
 60         return;
 61     }
 62     ll x,y,z,c,g; int i,j;
 63     while(1)
 64     {
 65         x=y=rand()%n; c=rand()%n;
 66         i=0,j=1,z=1;
 67         while(1)
 68         {
 69             i++;
 70             x=mul(x,x,n)+c; if(x>=n) x-=n;
 71             z=mul(z,max(y-x,x-y),n);
 72             if((i%178==0)||i==j)
 73             {
 74                 g=gcd(z,n);
 75                 if(g>1)
 76                 {
 77                     a[++h]=g;
 78                     while(n%g==0) n/=g;
 79                     Pollard_Rho(n);
 80                     return;
 81                 }
 82                 if(i==j) y=x,j<<=1;
 83             }
 84         }
 85     }
 86 }
 87  
 88 int main()
 89 {
 90     srand(time(0));
 91     scanf("%lld",&n);
 92     Pollard_Rho(n);
 93     sort(a+1,a+1+h);
 94     for (R i=1;i<=h;++i)
 95     {
 96         if(a[i]==a[i-1]) continue;
 97         n=n/a[i]*(a[i]-1);
 98     }
 99     printf("%lld",n);
100     return 0;
101 }

欧拉函数

　　「攻略」：https://www.lydsy.com/JudgeOnline/problem.php?id=3252

　　题意概述：从根节点走到某个叶子的权值为链上所有点的点权和，但多次走只能算一次，选出 $k$ 条根路径，使得总权值最大。$n<=200000$

　　其实就是贪心啦。发现第一次走的必然是那条权值最大的链，且后面的不会影响前面的（没有必要将前面的决策变得更劣）,所以做一个类似于长链剖分的东西，每个点和权值最大的儿子连到一起，最后对所有的链的权值排序，取前k大，如果不足就补0.

 1 # include <cstdio>
 2 # include <iostream>
 3 # include <algorithm>
 4 # define R register int
 5 # define ll long long
 6  
 7 using namespace std;
 8  
 9 const int maxn=200005;
10 int n,k,h,firs[maxn],x,y,dep[maxn];
11 int col[maxn],id;
12 ll lv[maxn],ans,v[maxn];
13 struct edge { int too,nex; }g[maxn<<1];
14  
15 void add (int x,int y)
16 {
17     g[++h].nex=firs[x];
18     firs[x]=h;
19     g[h].too=y;
20 }
21  
22 void dfs (int x)
23 {
24     int j,son=x;
25     ll maxs=-1;
26     for (R i=firs[x];i;i=g[i].nex)
27     {
28         j=g[i].too;
29         if(dep[j]) continue;
30         dep[j]=dep[x]+1;
31         dfs(j);
32         if(lv[ col[j] ]>=maxs) maxs=lv[ col[j] ],son=j;   
33     }
34     if(son==x) col[x]=++id;
35     lv[ col[son] ]+=v[x];
36     col[x]=col[son];
37 }
38  
39 int main()
40 {
41     scanf("%d%d",&n,&k);
42     for (R i=1;i<=n;++i) scanf("%lld",&v[i]);
43     for (R i=1;i<n;++i)
44     {
45         scanf("%d%d",&x,&y);
46         add(x,y); add(y,x);
47     }
48     dep[1]=1;
49     dfs(1);
50     sort(lv+1,lv+1+id);
51     for (R i=id;i>=1;--i)
52         if(k) ans+=lv[i],k--;
53     printf("%lld",ans);
54     return 0;
55 }

攻略

　　「淘金」：https://www.lydsy.com/JudgeOnline/problem.php?id=3131

　　题意概述：初始有一个 $n \times n $的网格，每个点有一块金子，现在每个点的金子转移到 $(f(x),f(y))$ 上去，$f(x)$ 定义为每个数位的乘积，如果跑出了$(n,n)$ 的范围，视为消失了。现在可以取 $k$ 次金子，求最多可以取到多少块金子。$n<=10^{12},k<=10^5$

　　首先，横纵坐标是独立的，可以单独处理。因为每个数位只包含 $2,3,5,7$ 四个质因子，且要求乘完的结果不能超过 $n$ ，可以发现乘积的种类数并不会很多...即使是极限数据也只有不到 $15000$ 种，所以就可以愉快的数位dp了。dp完就可以得到每个横行和每个纵列上的金子总数，则问题转化为在两个数组中各取一个的乘积的前k大，是一个比较基础的问题，用堆来实现即可。

 1 # include <cstdio>
 2 # include <iostream>
 3 # include <tr1/unordered_map>
 4 # include <algorithm>
 5 # include <queue>
 6 # define R register int
 7 # define ll long long
 8 # define pac(a,b) make_pair(a,b)
 9  
10 using namespace std;
11  
12 const int mod=1000000007;
13 int h,a[15],k,cnt,s[15000];
14 ll n,vis[15000],ans,dp[14][2][2][15000];
15 tr1::unordered_map <ll,int> m;
16 ll fm[15000];
17 typedef pair <ll,ll> pii;
18 priority_queue <pii,vector<pii>,less<pii> > q;
19  
20 bool cmp (int a,int b) { return a>b; }
21  
22 int main()
23 {
24     scanf("%lld",&n);
25     scanf("%d",&k);
26     for (ll i=1;i<=n;i*=2)
27         for (ll j=1;i*j<=n;j*=3)
28             for (ll k=1;i*j*k<=n;k*=5)
29                 for (ll z=1;i*j*k*z<=n;z*=7)
30                     if(i*j*k*z<=n) m[ i*j*k*z ]=++cnt,fm[cnt]=i*j*k*z;
31     while(n) { a[++h]=n%10; n/=10; }
32     for (R i=1;i<=h/2;++i) swap(a[i],a[h-i+1]);
33     dp[0][1][0][1]=1;
34     for (R i=0;i<h;++i)
35         for (R j=0;j<=1;++j)
36             for (R k=0;k<=1;++k)
37                 for (R z=1;z<=cnt;++z)
38                 {
39                     ll t=dp[i][j][k][z];
40                     if(!t) continue;
41                     for (R x=0;x<=9;++x)
42                     {
43                         int nj,nk,nz;
44                         if(j==1&&x>a[i+1]) continue;
45                         if(j==1&&x==a[i+1]) nj=1; else nj=0;
46                         if(k==0&&x==0) nk=0; else nk=1;
47                         if(k!=0&&x==0) continue;
48                         if(nk==0)
49                         {
50                             dp[i+1][nj][nk][z]=dp[i+1][nj][nk][z]+t;        
51                             continue;
52                         }
53                         nz=m[1LL*fm[z]*x];
54                         dp[i+1][nj][nk][nz]=dp[i+1][nj][nk][nz]+t;
55                     }
56                 }
57     for (R i=1;i<=cnt;++i)
58         vis[i]=dp[h][0][1][i]+dp[h][1][1][i];
59     sort(vis+1,vis+1+cnt,cmp);
60     for (R i=1;i<=cnt;++i)
61     {
62         s[i]=1;
63         q.push(pac(vis[i]*vis[1],i));
64     }
65     for (R i=1;i<=k;++i)
66     {
67         if(q.empty()) break;
68         pii t=q.top(); q.pop();
69         int ts=t.second;
70         ans=(ans+t.first)%mod;
71         if(s[ts]>=k) continue;
72         s[ts]++;
73         q.push(pac(vis[ts]*vis[ s[ts] ],ts));
74     }
75     printf("%lld",ans);
76     return 0;
77 }

淘金

　　「密钥破解」：https://www.lydsy.com/JudgeOnline/problem.php?id=4522

　　难度在于读题，读懂后就发现又是一道Pollard-Rho板子。

 1 # include <cstdio>
 2 # include <iostream>
 3 # include <tr1/unordered_map>
 4 # include <algorithm>
 5 # include <queue>
 6 # define R register int
 7 # define ll long long
 8 # define pac(a,b) make_pair(a,b)
 9  
10 using namespace std;
11  
12 const int mod=1000000007;
13 int h,a[15],k,cnt,s[15000];
14 ll n,vis[15000],ans,dp[14][2][2][15000];
15 tr1::unordered_map <ll,int> m;
16 ll fm[15000];
17 typedef pair <ll,ll> pii;
18 priority_queue <pii,vector<pii>,less<pii> > q;
19  
20 bool cmp (int a,int b) { return a>b; }
21  
22 int main()
23 {
24     scanf("%lld",&n);
25     scanf("%d",&k);
26     for (ll i=1;i<=n;i*=2)
27         for (ll j=1;i*j<=n;j*=3)
28             for (ll k=1;i*j*k<=n;k*=5)
29                 for (ll z=1;i*j*k*z<=n;z*=7)
30                     if(i*j*k*z<=n) m[ i*j*k*z ]=++cnt,fm[cnt]=i*j*k*z;
31     while(n) { a[++h]=n%10; n/=10; }
32     for (R i=1;i<=h/2;++i) swap(a[i],a[h-i+1]);
33     dp[0][1][0][1]=1;
34     for (R i=0;i<h;++i)
35         for (R j=0;j<=1;++j)
36             for (R k=0;k<=1;++k)
37                 for (R z=1;z<=cnt;++z)
38                 {
39                     ll t=dp[i][j][k][z];
40                     if(!t) continue;
41                     for (R x=0;x<=9;++x)
42                     {
43                         int nj,nk,nz;
44                         if(j==1&&x>a[i+1]) continue;
45                         if(j==1&&x==a[i+1]) nj=1; else nj=0;
46                         if(k==0&&x==0) nk=0; else nk=1;
47                         if(k!=0&&x==0) continue;
48                         if(nk==0)
49                         {
50                             dp[i+1][nj][nk][z]=dp[i+1][nj][nk][z]+t;        
51                             continue;
52                         }
53                         nz=m[1LL*fm[z]*x];
54                         dp[i+1][nj][nk][nz]=dp[i+1][nj][nk][nz]+t;
55                     }
56                 }
57     for (R i=1;i<=cnt;++i)
58         vis[i]=dp[h][0][1][i]+dp[h][1][1][i];
59     sort(vis+1,vis+1+cnt,cmp);
60     for (R i=1;i<=cnt;++i)
61     {
62         s[i]=1;
63         q.push(pac(vis[i]*vis[1],i));
64     }
65     for (R i=1;i<=k;++i)
66     {
67         if(q.empty()) break;
68         pii t=q.top(); q.pop();
69         int ts=t.second;
70         ans=(ans+t.first)%mod;
71         if(s[ts]>=k) continue;
72         s[ts]++;
73         q.push(pac(vis[ts]*vis[ s[ts] ],ts));
74     }
75     printf("%lld",ans);
76     return 0;
77 }

密钥破解

　　「数颜色」：https://www.lydsy.com/JudgeOnline/problem.php?id=2120

　　题意概述：给定一个数列，要求支持如下操作：询问一段区间的颜色种类数；修改某个位置的颜色。$n,m<=10^4$

　　带修莫队。将时间也视为一维，序列分块时块的大小设为 $n^{\frac{2}{3}}$,首先按照左端点的块排序，然后是右端点的块，最后是时间。复杂度可以证明是$n^{\frac{5}{3}}$.

 1 # include <cstdio>
 2 # include <iostream>
 3 # include <cmath>
 4 # include <algorithm>
 5 # define R register int
 6  
 7 using namespace std;
 8  
 9 const int maxn=1000006;
10 int n,m,x,y,st,tim;
11 int v[maxn],ans[maxn],lst[maxn],t[maxn];
12 int block_siz,b[maxn],vis[maxn],an;
13 char opt[2];
14 struct ask { int id,l,r,t; }s[maxn];
15 struct chan { int x,y,las; }c[maxn];
16  
17 bool cmp (ask x,ask y)
18 {
19     if(b[ x.l ]!=b[ y.l ]) return b[ x.l ]<b[ y.l ];
20     if(b[ x.r ]!=b[ y.r ]) return b[ x.r ]<b[ y.r ];
21     return x.t<y.t;
22 }
23  
24 void add (int x) { if(t[x]==0) an++; t[x]++; }
25 void del (int x) { if(t[x]==1) an--; t[x]--; }
26  
27 int read()
28 {
29     R x=0;
30     char c=getchar();
31     while (!isdigit(c)) c=getchar();
32     while (isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar();
33     return x;
34 }
35  
36 int main()
37 {
38     scanf("%d%d",&n,&m);
39     for (R i=1;i<=n;++i)
40         v[i]=read(),lst[i]=v[i];
41     for (R i=1;i<=m;++i)
42     {
43         scanf("%s",opt);
44         x=read(),y=read();
45         if(opt[0]=='Q') 
46         {
47             st++;
48             s[st].id=st;
49             s[st].l=x;
50             s[st].r=y;
51             s[st].t=tim;
52         }
53         else
54         {
55             c[++tim].x=x;
56             c[tim].y=y;
57             c[tim].las=lst[ c[tim].x ];
58             lst[ c[tim].x ]=y;
59         }   
60     }
61     int block_siz=pow(n,(double)2/3);
62     for (R i=1;i<=n;++i) b[i]=i/block_siz+1;
63     sort(s+1,s+1+st,cmp);
64     int l=1,r=0,t=0;
65     for (R i=1;i<=st;++i)
66     {
67         while(r<s[i].r) r++,add(v[r]);
68         while(r>s[i].r) del(v[r]),r--;
69         while(l<s[i].l) del(v[l]),l++;
70         while(l>s[i].l) l--,add(v[l]);
71         while(t<s[i].t)
72         {
73             t++;
74             if(l<=c[t].x&&c[t].x<=r) del(v[ c[t].x ]),add(c[t].y);
75             v[ c[t].x ]=c[t].y;
76         }
77         while(t>s[i].t)
78         {
79             if(l<=c[t].x&&c[t].x<=r) add(c[t].las),del(c[t].y);
80             v[ c[t].x ]=c[t].las;
81             t--;
82         }
83         ans[ s[i].id ]=an;
84     }
85     for (R i=1;i<=st;++i) printf("%d\n",ans[i]);
86     return 0;
87 }

数颜色

4.11：

　　「哈希冲突」：https://www.luogu.org/problemnew/show/P3396

　　题意概述：给定一个数列，每个位置有一个数，要求支持：修改某个数；询问$\%p$ 意义下 $=x$ 的位置的权值和。$n<=150000$

　　如果 $p$ 很大，那么暴力查询就是可行的，如果 $p$ 很小，就可以考虑动态维护所有答案。

　　将 $\sqrt{n}$ 作为一个分界点，小于它的维护所有答案，大于它的暴力查询，总复杂度 $N\sqrt{N}$

　　据说这个叫做根号分治。

 1 // luogu-judger-enable-o2
 2 # include <cstdio>
 3 # include <iostream>
 4 # include <cmath>
 5 # define R register int
 6 
 7 using namespace std;
 8 
 9 const int maxn=150005;
10 int n,m,x,y,sn;
11 int a[maxn],ans[400][400];
12 char opt[2];
13 
14 int ask (int x,int y)
15 {
16     int ans=0;
17     for (R i=y;i<=n;i+=x) ans+=a[i];
18     return ans;
19 }
20 
21 void init()
22 {
23     for (R i=1;i<=sn;++i)
24         for (R j=1;j<=n;++j)
25             ans[i][ j%i ]+=a[j];            
26 }
27 
28 void change (int x,int y)
29 {
30     for (R i=1;i<=sn;++i)
31         ans[i][ x%i ]=ans[i][ x%i ]-a[x]+y;
32     a[x]=y;
33 }
34 
35 int main()
36 {
37     scanf("%d%d",&n,&m);
38     for (R i=1;i<=n;++i)
39         scanf("%d",&a[i]);
40     sn=sqrt(n);
41     init();
42     for (R i=1;i<=m;++i)
43     {
44         scanf("%s",opt);
45         scanf("%d%d",&x,&y);
46         if(opt[0]=='A')
47         {
48             if(x<=sn) printf("%d\n",ans[x][y]);
49             else printf("%d\n",ask(x,y));
50         }
51         else
52             change(x,y);
53     }
54     return 0;
55 }

哈希冲突

　　「Count on a tree II」：https://www.luogu.org/problemnew/show/SP10707

　　题意概述：求树上两点间路径上颜色的种类数。$n<=4\times 10^4,m<=10^5$

　　树上莫队。求出树的欧拉序，即递归进入这个点时加入一次，离开这个点时再加入一次。这个序列非常神奇，首先在欧拉序上定位两点，两点间的路径上的点恰好在欧拉序中出现奇数次，而不在路径上的点则是偶数次。LCA可能会不在欧拉序里面，特判一下即可。注意，如果两个点存在祖孙关系，那么定位的两个点应为$begin[x],begin[y]$，否则则为 $end[x],begin[y]$.

Count on a tree II

　　「糖果公园」：https://www.lydsy.com/JudgeOnline/problem.php?id=3052

　　这题没什么好说的，就是树上莫队带修，或者说带修莫队上树。

  1 # include <cstdio>
  2 # include <iostream>
  3 # include <cmath>
  4 # include <algorithm>
  5 # define R register int
  6 # define ll long long
  7 # define getchar() (S==T&&(T=(S=BB)+fread(BB,1,1<<20,stdin),S==T)?EOF:*S++)
  8  
  9 using namespace std;
 10  
 11 const int maxn=200005;
 12 char BB[1 << 20], *S = BB, *T = BB; 
 13 int n,m,q,x,y,h,st,tim,tp,opt,siz;
 14 int firs[maxn],lst[maxn],a[maxn],beg[maxn],ed[maxn];
 15 int f[maxn][20],b[maxn],t[maxn],dep[maxn],c[maxn];
 16 ll an=0,ans[maxn],v[maxn],w[maxn];
 17 int vis[maxn],lg[maxn];
 18 struct edge { int too,nex; }g[maxn];
 19 struct ask { int l,r,id,t,lca; }s[maxn];
 20 struct chan { int x,y,las; }ch[maxn];
 21  
 22 int lca (int x,int y)
 23 {
 24     if(dep[x]>dep[y]) swap(x,y);
 25     for (R i=lg[ dep[y] ];i>=0;--i) if(dep[y]-(1<<i)>=dep[x]) y=f[y][i];
 26     if(x==y) return x;
 27     for (R i=lg[ dep[x] ];i>=0;--i)
 28         if(f[x][i]!=f[y][i])
 29             x=f[x][i],y=f[y][i];
 30     return f[x][0];
 31 }
 32  
 33 void dfs (int x)
 34 {
 35     a[++tp]=x; beg[x]=tp;
 36     int j;
 37     for (R i=firs[x];i;i=g[i].nex)
 38     {
 39         j=g[i].too;
 40         if(dep[j]) continue;
 41         dep[j]=dep[x]+1;
 42         f[j][0]=x;
 43         for (R k=1;k<=lg[ dep[j] ];++k) f[j][k]=f[ f[j][k-1] ][k-1];
 44         dfs(j);
 45     }
 46     a[++tp]=x; ed[x]=tp;
 47 }
 48  
 49 void add (int x,int y)
 50 {
 51     g[++h].nex=firs[x];
 52     firs[x]=h;
 53     g[h].too=y;
 54 }
 55  
 56 bool cmp (ask x,ask y)
 57 {
 58     if(b[ x.l ]!=b[ y.l ]) return x.l<y.l;
 59     if(b[ x.r ]!=b[ y.r ]) return x.r<y.r;
 60     return x.t<y.t;
 61 }
 62  
 63 void add (int x) //加入一个x糖
 64 {
 65     an+=v[x]*w[ t[x]+1 ];
 66     t[x]++;
 67 }
 68  
 69 void del (int x)
 70 {
 71     an-=v[x]*w[ t[x] ];
 72     t[x]--;
 73 }
 74  
 75 void chan (int x)
 76 {
 77     if(vis[x]) del(c[x]);
 78     else add(c[x]);
 79     vis[x]^=1;
 80 }
 81  
 82 int read()
 83 {
 84     R x=0;
 85     char c=getchar();
 86     while (!isdigit(c)) c=getchar();
 87     while (isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar();
 88     return x;
 89 }
 90  
 91 int main()
 92 {
 93     scanf("%d%d%d",&n,&m,&q);
 94     for (R i=1;i<=m;++i) v[i]=read();
 95     for (R i=1;i<=n;++i) w[i]=read();
 96     for (R i=1;i<n;++i)
 97     {
 98         x=read(),y=read();
 99         add(x,y); add(y,x);
100     }
101     for (R i=2;i<=n;++i) lg[i]=lg[i>>1]+1;
102     dep[1]=1; dfs(1);
103     for (R i=1;i<=n;++i) c[i]=read(),lst[i]=c[i];
104     for (R i=1;i<=q;++i)
105     {
106         opt=read(),x=read(),y=read();
107         if(opt==0)
108         {
109             tim++;
110             ch[tim].x=x;
111             ch[tim].y=y;
112             ch[tim].las=lst[ ch[tim].x ];
113             lst[ ch[tim].x ]=y;
114         }
115         else
116         {
117             s[++st].t=tim;
118             s[st].lca=lca(x,y);
119             if(beg[x]>beg[y]) swap(x,y);
120             if(s[st].lca==x) s[st].l=beg[x],s[st].r=beg[y];
121             else s[st].l=ed[x],s[st].r=beg[y];
122             s[st].id=st;
123         }
124     }
125     siz=pow(2*n,(double)2/3);
126     for (R i=1;i<=2*n;++i) b[i]=i/siz+1;
127     sort(s+1,s+1+st,cmp);
128     int l=1,r=0,t=0;
129     for (R i=1;i<=st;++i)
130     {
131         while(r<s[i].r) r++,chan(a[r]);
132         while(r>s[i].r) chan(a[r]),r--;
133         while(l<s[i].l) chan(a[l]),l++;
134         while(l>s[i].l) l--,chan(a[l]);
135         while(t>s[i].t)
136         {
137             if(vis[ ch[t].x ])
138             {
139                 del(c[ ch[t].x ]);
140                 add(ch[t].las);
141             }
142             c[ ch[t].x ]=ch[t].las;
143             t--;
144         }
145         while(t<s[i].t)
146         {
147             t++;
148             if(vis[ ch[t].x ])
149             {
150                 add(ch[t].y);
151                 del(c[ ch[t].x ]);
152             }
153             c[ ch[t].x ]=ch[t].y;
154         }
155         if(vis[ s[i].lca ]==0)
156         {
157             add(c[ s[i].lca ]);
158             ans[ s[i].id ]=an;
159             del(c[ s[i].lca ]);
160         }else ans[ s[i].id ]=an;
161     }
162     for (R i=1;i<=st;++i) printf("%lld\n",ans[i]);
163     return 0;
164 }

糖果公园

　　「矩阵乘法」：https://www.lydsy.com/JudgeOnline/problem.php?id=2738

　　题意概述：给定一个 $n\times n$ 的矩阵，$m$ 次询问子矩阵的 $k$ 小值。$n<=500,m<=60000$

　　二维树状数组+整体二分，没了。

 1 # include <cstdio>
 2 # include <iostream>
 3 # include <algorithm>
 4 # define R register int
 5  
 6 using namespace std;
 7  
 8 const int maxn=500005;
 9 int t[505][505];
10 int n,q,x,cnt,ans[maxn];
11 struct chan { int x,y,v; }c[maxn];
12 struct ask { int a,b,c,d,k,id; }a[maxn],t1[maxn],t2[maxn];
13  
14 void add (int x,int y,int v)
15 {
16     for (R i=x;i<=n;i+=(i&(-i)))
17         for (R j=y;j<=n;j+=(j&(-j)))
18             t[i][j]+=v;
19 }
20  
21 int ask (int x,int y)
22 {
23     int ans=0;
24     for (R i=x;i;i-=(i&(-i)))
25         for (R j=y;j;j-=(j&(-j)))
26             ans+=t[i][j];
27     return ans;
28 }
29  
30 bool cmp (chan a,chan b) { return a.v<b.v; }
31  
32 int askk (int a,int b,int c,int d)
33 {
34     return ask(c,d)-ask(a-1,d)-ask(c,b-1)+ask(a-1,b-1);
35 }
36  
37 void solve (int l,int r,int sl,int sr)
38 {
39     if(l==r)
40     {
41         for (R i=sl;i<=sr;++i)
42             ans[ a[i].id ]=c[l].v;
43         return;
44     }
45     int s,h1=0,h2=0,mid=(l+r)>>1,h=sl-1;
46     for (R i=l;i<=mid;++i) add(c[i].x,c[i].y,1);
47     for (R i=sl;i<=sr;++i)
48     {
49         s=askk(a[i].a,a[i].b,a[i].c,a[i].d);
50         if(s>=a[i].k) t1[++h1]=a[i];
51         else t2[++h2]=a[i],t2[h2].k-=s;
52     }
53     for (R i=1;i<=h1;++i) a[++h]=t1[i];
54     for (R i=1;i<=h2;++i) a[++h]=t2[i];
55     for (R i=l;i<=mid;++i) add(c[i].x,c[i].y,-1);
56     solve(l,mid,sl,sl+h1-1);
57     solve(mid+1,r,sl+h1,sr);
58 }
59  
60 int main()
61 {
62     scanf("%d%d",&n,&q);
63     for (R i=1;i<=n;++i)
64         for (R j=1;j<=n;++j)
65         {
66             scanf("%d",&x);
67             c[++cnt].x=i;
68             c[cnt].y=j;
69             c[cnt].v=x;
70         }
71     for (R i=1;i<=q;++i)
72         scanf("%d%d%d%d%d",&a[i].a,&a[i].b,&a[i].c,&a[i].d,&a[i].k),a[i].id=i;
73     sort(c+1,c+1+cnt,cmp);
74     solve(1,cnt,1,q);
75     for (R i=1;i<=q;++i)
76         printf("%d\n",ans[i]);
77     return 0;
78 }

矩阵乘法

　　「圆上的整点」：https://www.lydsy.com/JudgeOnline/problem.php?id=1041

　　题意概述：求 $x^2+y^2=r^2$ 这个圆上有多少个点的坐标为整数。$r<=2\times 10^9$

　　一道结论题，如果不知道恐怕就没法做。看这里　　

 1 # include <cstdio>
 2 # include <iostream>
 3 # define R register int
 4 # define ll long long
 5  
 6 using namespace std;
 7  
 8 int n;
 9 int a1,a2,t;
10 ll ans=4;
11  
12 int main()
13 {
14     scanf("%lld",&n);
15     for (R i=2;i*i<=n;i++)
16     {
17         if(n%i) continue;
18         t=0;
19         while(n%i==0)
20         {
21             n/=i;
22             t+=2;
23         }
24         if(i%4==1) ans=ans*(t+1);
25     }
26     if(n>1&&n%4==1) ans*=3;
27     printf("%lld",ans);
28     return 0;
29 }
30

圆上的整点

　　「排序机械臂」：https://www.lydsy.com/JudgeOnline/problem.php?id=3506

　　Splay区间翻转模板题，就是练练手。

  1 # include <cstdio>
  2 # include <iostream>
  3 # include <algorithm>
  4 # define R register int
  5  
  6 using namespace std;
  7  
  8 const int maxn=100005;
  9 int n,x,rt;
 10 int v[maxn],delta[maxn];
 11 int ch[maxn][2],siz[maxn],f[maxn];
 12 struct node { int v,id; }a[maxn];
 13  
 14 void update (int x)
 15 {
 16     siz[x]=siz[ ch[x][0] ]+siz[ ch[x][1] ]+1;
 17 }
 18  
 19 int build (int l,int r,int g)
 20 {
 21     if(l>r) return 0;
 22     int mid=(l+r)>>1;
 23     int x=v[mid];
 24     f[x]=g;
 25     if(l!=r)
 26     {
 27         ch[x][0]=build(l,mid-1,x);
 28         ch[x][1]=build(mid+1,r,x);
 29     }
 30     update(x);
 31     return x;
 32 }
 33  
 34 bool cmp (node a,node b) { if(a.v!=b.v) return a.v<b.v; return a.id<b.id; }
 35  
 36 void rev (int x)
 37 {
 38     delta[x]^=1;
 39     swap(ch[x][0],ch[x][1]);
 40 }
 41  
 42 void pushdown (int x)
 43 {
 44     delta[x]=0;
 45     rev(ch[x][0]);
 46     rev(ch[x][1]);
 47 }
 48  
 49 int find (int k)
 50 {
 51     int s,x=rt;
 52     while(1)
 53     {
 54         if(delta[x]) pushdown(x);
 55         s=siz[ ch[x][0] ];
 56         if(s>=k) x=ch[x][0];
 57         else if(s+1==k) return x;
 58         else x=ch[x][1],k-=s+1;
 59     }
 60 }
 61  
 62 int D (int x) { return ch[ f[x] ][1]==x; }
 63  
 64 void rotate (int x)
 65 {
 66     if(delta[ f[x] ]) pushdown(f[x]);
 67     if(delta[x]) pushdown(x);
 68     int F=f[x],g=f[F],d=D(x),df=D(F);
 69     int k=ch[x][d^1];
 70     ch[x][d^1]=F;
 71     ch[F][d]=k;
 72     ch[g][df]=x;
 73     f[k]=F; f[F]=x; f[x]=g;
 74     update(F);
 75     update(x);
 76 }
 77  
 78 void Splay (int x,int goa)
 79 {
 80     while(f[x]!=goa)
 81     {
 82         int F=f[x],g=f[F];
 83         if(g==goa) rotate(x);
 84         else if(D(F)==D(x)) rotate(F),rotate(x);
 85         else rotate(x),rotate(x);
 86     }
 87     if(!goa) rt=x;
 88 }
 89  
 90 int main()
 91 {
 92     scanf("%d",&n);
 93     for (R i=1;i<=n;++i)
 94     {
 95         scanf("%d",&a[i].v);
 96         a[i].id=i;
 97     }
 98     sort(a+1,a+1+n,cmp);
 99     for (R i=1;i<=n;++i)
100         v[ a[i].id+1 ]=i;
101     v[1]=n+1; v[n+2]=n+2;
102     rt=build(1,n+2,0);
103     for (R i=1;i<=n;++i)
104     {
105         Splay(i,0);
106         int s=siz[ ch[i][0] ];
107         printf("%d ",s);
108         int l=find(i);
109         int r=find(s+2);
110         Splay(l,0); Splay(r,l);
111         rev(ch[r][0]);
112     }
113     return 0;
114 }

排序机械臂

4.12：

　　「自适应辛普森法1」：https://www.luogu.org/problemnew/show/P4525

　　自适应辛普森太强了。就是把一个比较复杂的函数用二次函数来拟合，因为二次函数比较好算，且有弧度，拟合效果不错。

　　二次函数底下的面积用的是这个公式：$(r-l)\frac{f(l)+f(r)+4\times f(mid)}{6}$，用微积分简单地推一推就可以得到。

　　递归求解，如果发现一个区域分成两半后分别求解的答案和直接求解的答案相差不大，就返回，否则继续递归求解。

 1 # include <cstdio>
 2 # include <iostream>
 3 # include <cmath>
 4 
 5 using namespace std;
 6 
 7 const double eps=1e-10;
 8 double a,b,c,d,l,r;
 9 
10 double f (double x)
11 {
12     return (c*x+d)/(a*x+b);
13 }
14 
15 double simpson (double l,double r)
16 {
17     double mid=(l+r)/2;
18     return (r-l)*(f(l)+f(r)+4*f(mid))/6;
19 }
20 
21 double ask (double l,double r)
22 {
23     double mid=(l+r)/2;
24     double ans1=simpson(l,r),ans2=simpson(l,mid)+simpson(mid,r);
25     if(fabs(ans1-ans2)<=eps) return ans1;
26     return ask(l,mid)+ask(mid,r);
27 }
28 
29 int main()
30 {
31     scanf("%lf%lf%lf%lf%lf%lf",&a,&b,&c,&d,&l,&r);
32     printf("%.6lf",ask(l,r));
33     return 0;
34 }

自适应辛普森法1

　　「龙与地下城」：https://www.lydsy.com/JudgeOnline/problem.php?id=4909

　　题意概述：掷 $y$ 个骰子，每个骰子不会超过$x$ 面，多组询问求总点数落在 $[a,b]$ 区域的概率。$x<=20,y<=2000000$.

　　过于蛇皮，引起不适

　　比较好想的就是dp啦，用FFT+快速幂来做。注意每次乘完要清空虚部，否则精度会上天。

　　正解和这一点关系也没有，进一步引起不适。要解决它，你可能需要看看数学选修2-3的课本，学学正态分布什么的，还需要知道一个中心极限定理（然而这个数学书上是没有的）。正态分布的概率密度函数如下：

　　$$\frac{1}{\sqrt{2\pi \sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$

　　本题的答案符合正态分布，但还需要变变形。如果有 $n$ 个独立分布的随机变量，那么设：

　　$$Y=\frac{\sum_{i=1}^nx_i-n\mu}{\sqrt{n\sigma^2}}$$

　　当 $n$ 足够大时，这里的 $Y$ 是满足正态分布 $N(0,1)$ 的，所以把

　　$$[\frac{A-n\mu}{\sqrt{n\sigma^2}},\frac{B-n\mu}{\sqrt{n\sigma^2}}]$$

　　这个区间愉快的辛普森积分出来就好了。

　　然而还是不对，因为刚刚说过“当 $n$ 足够大时”，而有时候 $n$ 并不是很够大，这时候接着上 $FFT$ 就好了。

  1 # include <cstdio>
  2 # include <iostream>
  3 # include <cmath>
  4 # include <cstring>
  5 # define R register int
  6 # define lb double
  7 
  8 using namespace std;
  9 
 10 const int maxn=1000006;
 11 const lb Pi=acos(-1);
 12 const lb eps=1e-12;
 13 int T,len,A,B,ln;
 14 int x,y,rev[maxn];
 15 lb s,qs[maxn],mu,ro,af,bf;
 16 double ts;
 17 struct complex 
 18 {   
 19     lb r,c;
 20     complex (lb rr=0,lb cc=0) { r=rr; c=cc; }
 21 }og,og1,t;
 22 complex operator + (complex a,complex b) { return complex(a.r+b.r,a.c+b.c); }
 23 complex operator - (complex a,complex b) { return complex(a.r-b.r,a.c-b.c); }
 24 complex operator * (complex a,complex b) { return complex(a.r*b.r-a.c*b.c,a.r*b.c+a.c*b.r); }
 25 complex f[maxn],g[maxn];
 26 complex a[maxn],ans[maxn];
 27 
 28 lb ab (lb x) { if(x<0) return -x; return x; }
 29 
 30 inline void FFT (complex *f,int v)
 31 {
 32     for (R i=0;i<len;++i) if(i<rev[i]) swap(f[i],f[ rev[i] ]);
 33     for (R i=2;i<=len;i<<=1)
 34     {
 35         ln=i>>1;
 36         og1=complex(cos(Pi/ln),v*sin(Pi/ln));
 37         for (R l=0;l<len;l+=i)
 38         {
 39             og=complex(1,0);
 40             for (R x=l;x<l+ln;++x)
 41             {
 42                 t=og*f[ln+x];
 43                 f[ln+x]=f[x]-t;
 44                 f[x]=f[x]+t;
 45                 og=og1*og;
 46             }
 47         }
 48     }
 49 }
 50 
 51 int mul (complex *a,complex *b,int lena,int lenb)
 52 {
 53     len=1; while(len<(lena+lenb)) len<<=1;
 54     for (R i=1;i<=len;++i) rev[i]=(rev[i>>1]>>1)|((i&1)?(len>>1):0);
 55     for (R i=0;i<=len;++i) f[i].r=f[i].c=g[i].r=g[i].c=0;
 56     for (R i=0;i<lena;++i)
 57         f[i]=a[i];
 58     for (R i=0;i<lenb;++i)
 59         g[i]=b[i];
 60     FFT(f,1); FFT(g,1);
 61     for (R i=0;i<len;++i) f[i]=f[i]*g[i];
 62     FFT(f,-1);
 63     for (R i=0;i<len;++i) f[i].r/=len,f[i].c=0;
 64     len=lena+lenb-1;
 65     for (R i=0;i<len;++i) a[i]=f[i];
 66     return len;
 67 }
 68 
 69 void qui (int b)
 70 {
 71     int al=x,ansl=1;
 72     ans[0].r=1; ansl=mul(ans,a,ansl,al);
 73     b--;
 74     while(b)
 75     {
 76         if(b&1) ansl=mul(ans,a,ansl,al);
 77         al=mul(a,a,al,al);
 78         b>>=1;
 79     }
 80 }
 81 
 82 double ff (double x)
 83 {
 84     return exp(-x*x/2.0)/sqrt(2*Pi);
 85 }
 86 
 87 double simpson (double l,double r)
 88 {
 89     double mid=(l+r)/2;
 90     return (r-l)*(ff(l)+ff(r)+4*ff(mid))/6;
 91 }
 92 
 93 double ask (double l,double r)
 94 {
 95     double mid=(l+r)/2;
 96     double ans1=simpson(l,r),ans2=simpson(l,mid)+simpson(mid,r);
 97     if(fabs(ans1-ans2)<=eps) return ans1;
 98     return ask(l,mid)+ask(mid,r);
 99 }
100 
101 const int num=400000;
102 
103 int main()
104 {
105     scanf("%d",&T);
106     while(T--)
107     {
108         scanf("%d%d",&x,&y);
109         if(x*y<=num)
110         {
111             memset(a,0,sizeof(a));
112             memset(ans,0,sizeof(ans));
113             for (R i=0;i<x;++i) a[i].r=(lb)1.0/x;
114             qui(y);
115             for (R i=1;i<=x*y;++i) qs[i]=qs[i-1]+ans[i-1].r;
116             int q=10;
117             while(q--)
118             {
119                 scanf("%d%d",&A,&B);
120                 s=qs[B+1]-qs[A];
121                 if(ab(s)<=eps) s=0;
122                 ts=s;
123                 printf("%.10lf\n",ts);
124             }
125         }
126         else
127         {
128             mu=(x-1)/2.0;
129             ro=(x*x-1.0)/12.0;
130             int q=10;
131             while(q--)
132             {
133                 scanf("%d%d",&A,&B);
134                 af=(A-mu*y)/(sqrt(ro*y));
135                 bf=(B-mu*y)/(sqrt(ro*y));
136                 printf("%.10lf\n",ask(0,bf)-ask(0,af));
137             }
138         }
139     }
140     return 0;
141 }

龙与地下城

　　「自适应辛普森法2」：https://www.luogu.org/problemnew/show/P4526

　　这道题相比板子，就是多了一个函数可能不收敛的奇怪情况。题解告诉我们，如果 $a<0$ 那么就不收敛，可是作为一个数学渣，我怎么可能推出这种东西，所以可以乱搞。画个图，发现当x比较小的时候，函数值比较大，当x比较大的时候，根据a的不同，有时候函数值很大，有时候很小。如果函数值一直很大，就没有办法积分，所以倍增一下，看看当x为何值时，函数值才开始变得很小，如果一直很大就视为发散，否则就视为收敛。这样做还有一点小小的问题，就是当$a=0$ 的时候可能会误判，怎么办呢？我选择特判。

 1 # include <cstdio>
 2 # include <iostream>
 3 # include <cmath>
 4 # define R register int
 5 
 6 using namespace std;
 7 
 8 const double inf=1e9;
 9 const double eps=1e-10;
10 double a;
11 
12 double f (double x)
13 {
14     return pow(x,(a-x*x)/x);
15 }
16 
17 double simpson (double l,double r)
18 {
19     double mid=(l+r)/2;
20     return (r-l)*(f(l)+f(r)+4*f(mid))/6;
21 }
22 
23 double ask (double l,double r)
24 {
25     double mid=(l+r)/2;
26     double ans1=simpson(l,r),ans2=simpson(l,mid)+simpson(mid,r);
27     if(fabs(ans1-ans2)<eps) return ans1;
28     return ask(l,mid)+ask(mid,r);
29 }
30 
31 int main()
32 {
33     scanf("%lf",&a);
34     double l=1,r=1;
35     while(r<=inf&&f(r)>eps) r*=2;
36     if(f(r)>eps) { puts("orz"); return 0; }
37     while(l>eps&&f(l)>eps) l/=2;
38     if(f(l)>eps&&a) { puts("orz"); return 0; }
39     printf("%.5lf",ask(l,r));
40     return 0;
41 }

自适应辛普森法2

4.13：

　　上午考试了，下午和晚上补课，所以几乎没做题。

　　「Guess the number」:https://codeforces.com/gym/101021/problem/A

　　晚上想打场 $CF$，结果发现有交互题，所以赶紧复习一下。这道题就是个二分查找，关键还是练习交互的格式问题。

　　做交互题输出时不要怕输出的回车太多，每输出一次就打个回车，清下缓存总是没有错的。

 1 # include <cstdio>
 2 # include <iostream>
 3 # include <cstring>
 4 
 5 using namespace std;
 6 
 7 char c[5];
 8 
 9 bool ask (int x)
10 {
11     printf("%d\n",x);
12     fflush(stdout);
13     scanf("%s",c+1);
14     if(c[1]=='<') return false;
15     return true;
16 }
17 
18 int main()
19 {
20     int l=1,r=1000000,ans;
21     while(l<=r)
22     {
23         int mid=(l+r)>>1;
24         if(ask(mid)) ans=mid,l=mid+1;
25         else r=mid-1;
26     }
27     printf("! %d",ans);
28     fflush(stdout);    
29     return 0;
30 }

CF101021 A

　　「Serval and Toy Bricks」：https://codeforces.com/contest/1153/problem/B

　　题意概述：有一个积木搭的玩具，给出主视图和俯视图，求一个可行的左视图。$n,m,h<=100$

　　发现如果每个块都放上主视图中那一列看起来的那么多是肯定没错的。再根据俯视图，将不能放积木的块清空。因为保证有解，这就是一个合法解了。

 1 # include <cstdio>
 2 # include <iostream>
 3 # define R register int
 4 
 5 using namespace std;
 6 
 7 const int maxn=200;
 8 int n,m,h,x; 
 9 int a[maxn][maxn];
10 
11 int main()
12 {
13     scanf("%d%d%d",&n,&m,&h);
14     for (R i=1;i<=m;++i)
15     {
16         scanf("%d",&x);
17         for (R j=1;j<=n;++j)
18             a[j][i]=x;
19     }
20     for (R i=1;i<=n;++i)
21     {
22         scanf("%d",&x);
23         for (R j=1;j<=m;++j)
24             a[i][j]=min(a[i][j],x);
25     }
26     for (R i=1;i<=n;++i)
27     {
28         for (R j=1;j<=m;++j)
29         {
30             scanf("%d",&x);
31             if(x) printf("%d ",a[i][j]);
32             else printf("0 ");
33         }
34         printf("\n");
35     }
36     return 0;
37 }

B - Serval and Toy Bricks

　　「Serval and Rooted Tree」：https://codeforces.com/contest/1153/problem/D

　　题意概述：给定一棵树，每个点有一个属性 $max~or~min$ ,如果是 $max$,则表示取所有叶子的最大值,否则取最小值,现在给定一些数,将它们安排到叶子上,并最大化根的值。$n<=3\times 10^5$

　　这题比较简单。本来以为需要二分，后来发现直接贪心就好。考虑每个点在自己的子树里最好能取到第几大的叶子的值，最后输出根节点的答案即可。对于 $min$ 节点，它的答案就是所有儿子的答案加起来，否则就是取一个最小值。

 1 # include <cstdio>
 2 # include <iostream>
 3 # define R register int
 4 
 5 using namespace std;
 6 
 7 const int maxn=300005;
 8 int n,a[maxn],x,k;
 9 int son[maxn],bro[maxn];
10 int lef[maxn],siz[maxn];
11 
12 void redfs (int x)
13 {
14     int ans=1000000000;
15     if(lef[x]) return;
16     for (R i=son[x];i;i=bro[i])
17     {
18         redfs(i);
19         if(!a[x]) siz[x]+=siz[i];
20         else ans=min(ans,siz[i]);
21     }
22     if(a[x]) siz[x]=ans;
23 }
24 
25 int main()
26 {
27     scanf("%d",&n);
28     for (R i=1;i<=n;++i) scanf("%d",&a[i]);
29     for (R i=2;i<=n;++i)
30     {
31         scanf("%d",&x);
32         bro[i]=son[x]; son[x]=i;
33     }
34     for (R i=1;i<=n;++i)
35         if(!son[i]) siz[i]=1,k++,lef[i]=1;
36     redfs(1);
37     printf("%d",k-siz[1]+1);
38     return 0;
39 }

D - Serval and Rooted Tree

4.14:

　　又是补课的一天；

4.15:

　　「divcntk」：https://www.luogu.org/problemnew/show/SP34096

　　题意概述：求 $\sum_{i=1}^n\sigma_0(i^k)$ ，$n<=10^10$

　　min_25板子，但我可能学的不大对。本来筛质数应该筛到 $\sqrt{N}$ ，但是有的时候却会错，多筛一点就对了？

　　首先这是一个积性函数，其次质数的幂可以快速求：$f(p^c)=ck+1$，然后套板子就可以了。

 1 # include <cstdio>
 2 # include <iostream>
 3 # include <cstring>
 4 # include <cmath>
 5 # define ll unsigned long long
 6 # define R register int
 7 
 8 using namespace std;
 9 
10 const int maxn=400005;
11 int T,vis[maxn],ph,m;
12 int id1[maxn],id2[maxn];
13 ll sn,n,k,v[maxn],pri[maxn],h[maxn],ans;
14 
15 void init (ll n)
16 {
17     ph=0;
18     for (R i=2;i<=(int)n;++i)
19     {
20         if(!vis[i]) pri[++ph]=i;
21         for (R j=1;j<=ph&&pri[j]*i<=n;++j)
22         {
23             vis[ i*pri[j] ]=1;
24             if(i%pri[j]==0) break;
25         }
26     }
27 }
28 
29 ll cal (ll x)
30 {
31     if(x<=sn) return id1[x];
32     return id2[n/x];
33 }
34 
35 ll g (ll n,int m)
36 {
37     if(n<=1||pri[m+1]>n) return 0;
38     ll ans=h[ cal(n) ]-(ll)(k+1)*m;
39     for (R i=m+1;i<=ph&&pri[i]*pri[i]<=n;++i)
40     {
41         ll p=pri[i];
42         for (R e=1;p<=n;e++,p*=pri[i])
43             ans=ans+((ll)e*k+1)*((e>1)+g(n/p,i));
44     }
45     return ans;
46 }
47 
48 int main()
49 {
50     scanf("%d",&T);
51     while(T--)
52     {
53         cin>>n>>k;
54         sn=sqrt(n);
55         init(sn+5);
56         m=0;
57         ll l=1,r;
58         while(l<=n)
59         {
60             r=n/(n/l); v[++m]=n/l;
61             if(v[m]<=sn) id1[ v[m] ]=m;
62             else id2[ n/v[m] ]=m;
63             h[m]=v[m]-1;
64             l=r+1;
65         }
66         for (R i=1;i<=ph;++i)
67             for (R j=1;j<=m&&pri[i]*pri[i]<=v[j];++j)
68             {
69                 int x=cal(v[j]/pri[i]);
70                 h[j]=h[j]-h[x]+i-1;
71             }
72         for (R i=1;i<=m;++i) h[i]*=(k+1);
73         ans=g(n,0)+1;
74         cout<<ans<<endl;
75     }
76     return 0;
77 }

divcntk

　　「divcnt2」:https://www.luogu.org/problemnew/show/SP20173

　　虽然有更好做法，但是，也可以把刚刚那题的k改成2.

 1 # include <cstdio>
 2 # include <iostream>
 3 # include <cstring>
 4 # include <cmath>
 5 # define ll unsigned long long
 6 # define R register int
 7 
 8 using namespace std;
 9 
10 const int maxn=5000006;
11 int T,vis[maxn],ph,m;
12 int id1[maxn],id2[maxn];
13 ll sn,n,k,v[maxn],pri[maxn],h[maxn],ans;
14 
15 void init (ll n)
16 {
17     ph=0;
18     for (R i=2;i<=(int)n;++i)
19     {
20         if(!vis[i]) pri[++ph]=i;
21         for (R j=1;j<=ph&&pri[j]*i<=n;++j)
22         {
23             vis[ i*pri[j] ]=1;
24             if(i%pri[j]==0) break;
25         }
26     }
27 }
28 
29 ll cal (ll x)
30 {
31     if(x<=sn) return id1[x];
32     return id2[n/x];
33 }
34 
35 ll g (ll n,int m)
36 {
37     if(n<=1||pri[m+1]>n) return 0;
38     ll ans=h[ cal(n) ]-(k+1)*m;
39     for (R i=m+1;i<=ph&&pri[i]*pri[i]<=n;++i)
40     {
41         ll p=pri[i];
42         for (R e=1;p<=n;e++,p*=pri[i])
43             ans=ans+((ll)e*k+1)*((e>1)+g(n/p,i));
44     }
45     return ans;
46 }
47 
48 int main()
49 {
50     scanf("%d",&T);
51     while(T--)
52     {
53         cin>>n; k=2;
54         sn=sqrt(n);
55         init(sn+1);
56         m=0;
57         ll l=1,r;
58         while(l<=n)
59         {
60             r=n/(n/l); v[++m]=n/l;
61             if(v[m]<=sn) id1[ v[m] ]=m;
62             else id2[ n/v[m] ]=m;
63             h[m]=v[m]-1;
64             l=r+1;
65         }
66         for (R i=1;i<=ph;++i)
67             for (R j=1;j<=m&&pri[i]*pri[i]<=v[j];++j)
68             {
69                 int x=cal(v[j]/pri[i]),y=cal(pri[i]-1);
70                 h[j]=h[j]-h[x]+h[y];
71             }
72         for (R i=1;i<=m;++i) h[i]*=(k+1);
73         ans=g(n,0)+1;
74         cout<<ans<<endl;
75     }
76     return 0;
77 }

divcnt2

　　「divcnt3」:https://www.luogu.org/problemnew/show/SP20174

　　再把2改成3.

 1 # include <cstdio>
 2 # include <iostream>
 3 # include <cstring>
 4 # include <cmath>
 5 # define ll unsigned long long
 6 # define R register int
 7 
 8 using namespace std;
 9 
10 const int maxn=5000006;
11 int T,vis[maxn],ph,m;
12 int id1[maxn],id2[maxn];
13 ll sn,n,k,v[maxn],pri[maxn],h[maxn],ans;
14 
15 void init (ll n)
16 {
17     ph=0;
18     for (R i=2;i<=(int)n;++i)
19     {
20         if(!vis[i]) pri[++ph]=i;
21         for (R j=1;j<=ph&&pri[j]*i<=n;++j)
22         {
23             vis[ i*pri[j] ]=1;
24             if(i%pri[j]==0) break;
25         }
26     }
27 }
28 
29 ll cal (ll x)
30 {
31     if(x<=sn) return id1[x];
32     return id2[n/x];
33 }
34 
35 ll g (ll n,int m)
36 {
37     if(n<=1||pri[m+1]>n) return 0;
38     ll ans=h[ cal(n) ]-(k+1)*m;
39     for (R i=m+1;i<=ph&&pri[i]*pri[i]<=n;++i)
40     {
41         ll p=pri[i];
42         for (R e=1;p<=n;e++,p*=pri[i])
43             ans=ans+((ll)e*k+1)*((e>1)+g(n/p,i));
44     }
45     return ans;
46 }
47 
48 int main()
49 {
50     scanf("%d",&T);
51     while(T--)
52     {
53         cin>>n; k=3;
54         sn=sqrt(n);
55         init(sn+1);
56         m=0;
57         ll l=1,r;
58         while(l<=n)
59         {
60             r=n/(n/l); v[++m]=n/l;
61             if(v[m]<=sn) id1[ v[m] ]=m;
62             else id2[ n/v[m] ]=m;
63             h[m]=v[m]-1;
64             l=r+1;
65         }
66         for (R i=1;i<=ph;++i)
67             for (R j=1;j<=m&&pri[i]*pri[i]<=v[j];++j)
68             {
69                 int x=cal(v[j]/pri[i]),y=cal(pri[i]-1);
70                 h[j]=h[j]-h[x]+h[y];
71             }
72         for (R i=1;i<=m;++i) h[i]*=(k+1);
73         ans=g(n,0)+1;
74         cout<<ans<<endl;
75     }
76     return 0;
77 }

divcnt3

　　「快速沃尔什变换」：https://www.luogu.org/problemnew/show/P4717

　　题意概述：这是一道模板题，请点击链接查看题面。

　　首先来看看or，首先对两个数组各求一遍高维前缀和，现在每个位置保留的就是子集和了，将对应位置相乘，得到的就是答案数组的高维前缀和（这里要好好理解一下），然后再用类似于高维前缀和的做法将其还原即可。

　　接下来是and，and和or非常类似，将子集和转变为超集和就可以了。

　　最后是xor，xor就比较复杂了，我只会归纳法证明，具体怎么回事也不是很清楚，所以直接放上来：

　　$FWT(A)=\begin{cases}(FWT(A_0)+FWT(A_1),FWT(A_0)-FWT(A_1)) & n>0\\A & n=0\end{cases}$

　　$IFWT(A)=(\frac{IFWT(A_0)+IFWT(A_1)}{2},\frac{IFWT(A_0)-IFWT(A_1)}{2})$

 1 // luogu-judger-enable-o2
 2 # include <cstdio>
 3 # include <iostream>
 4 # define R register int
 5 # define ll long long
 6 
 7 using namespace std;
 8 
 9 const int maxn=1<<18;
10 const int mod=998244353;
11 const ll inv_2=499122177;
12 ll A[maxn],B[maxn];
13 ll f[maxn],g[maxn];
14 int n;
15 
16 void giv()
17 {
18     for (R i=0;i<(1<<n);++i) f[i]=A[i];
19     for (R i=0;i<(1<<n);++i) g[i]=B[i];
20 }
21 
22 void mul()
23 {
24     for (R i=0;i<(1<<n);++i) f[i]=f[i]*g[i]%mod;
25 }
26 
27 void writeln()
28 {
29     for (R i=0;i<(1<<n);++i) printf("%d ",f[i]);
30     printf("\n");
31 }
32 
33 void fwt_or (ll *f,int v)
34 {
35     for (R i=0;i<n;++i)
36         for (R j=0;j<(1<<n);++j)
37             if(j&(1<<i)) f[j]=(f[j]+v*f[j^(1<<i)]+mod)%mod;
38 }
39 
40 void fwt_and (ll *f,int v)
41 {
42     for (R i=0;i<n;++i)
43         for (R j=0;j<(1<<n);++j)
44             if((j&(1<<i))==0) f[j]=(f[j]+v*f[j^(1<<i)]+mod)%mod;
45 }
46 
47 void fwt_xor (ll *f,int v)
48 {
49     for (R i=2;i<=(1<<n);i<<=1)
50     {
51         int ln=i>>1;
52         for (R b=0;b<(1<<n);b+=i)
53             for (R x=b;x<b+ln;++x)
54             {
55                 ll t=f[x+ln];
56                 f[x+ln]=(f[x]-t+mod)%mod;
57                 f[x]=(f[x]+t)%mod;
58                 if(v==-1) f[x]=f[x]*inv_2%mod,f[x+ln]=f[x+ln]*inv_2%mod;
59             }
60     }
61 }
62 
63 int main()
64 {
65     scanf("%d",&n);
66     for (R i=0;i<(1<<n);++i) scanf("%d",&A[i]);
67     for (R i=0;i<(1<<n);++i) scanf("%d",&B[i]);
68     
69     giv();
70     fwt_or(f,1); fwt_or(g,1);
71     mul();
72     fwt_or(f,-1);
73     writeln();
74 
75     giv();
76     fwt_and(f,1); fwt_and(g,1);
77     mul();
78     fwt_and(f,-1);
79     writeln();
80 
81     giv();
82     fwt_xor(f,1); fwt_xor(g,1);
83     mul();
84     fwt_xor(f,-1);
85     writeln();
86     return 0;
87 }

快速沃尔什变换

　　「Hard Nim」：https://www.lydsy.com/JudgeOnline/problem.php?id=4589

　　题意概述：两个人在玩取石子游戏，有 $n$ 堆石子，每堆石子的数量是不超过 $m$ 的质数，求后手必胜的方案数. $n<=10^9,m<=5\times 10^4$

　　这是一个最普通的 $nim$ 游戏，所以，当且仅当所有石子的异或值为 $0$ 时，后手必胜。

　　朴素dp绝对不行，因为n非常大，但是矩阵快速幂也不行，因为m也不小。

　　使用fwt恰好可以解决这两个问题，将初始序列和自己做 $n$ 次 $fwt$ 即可，可以使用快速幂，但这样太慢了。

　　注意到fwt与fft的一大区别就是不会越乘越长，所以可以直接在变换后的序列上做数字快速幂，最后再恢复，这样就只需要做两次fwt了。

 1 # include <cstdio>
 2 # include <iostream>
 3 # include <cstring>
 4 # define R register int
 5 # define ll long long
 6  
 7 const int maxn=(1<<17)+5;
 8 const int mod=1000000007;
 9 int n,m,h,len;
10 int pri[maxn],i,vis[maxn];
11 ll f[maxn];
12  
13 ll qui (ll a,ll b)
14 {
15     ll s=1;
16     while(b)
17     {
18         if(b&1) s=s*a%mod;
19         a=a*a%mod;
20         b>>=1;
21     }
22     return s;
23 }
24  
25 void fwt (ll *f,int v)
26 {
27     ll inv=qui(2,mod-2);
28     for (R i=2;i<=len;i<<=1)
29     {
30         int ln=i>>1;
31         for (R b=0;b<len;b+=i)
32             for (R x=b;x<b+ln;++x)
33             {
34                 ll t=f[x+ln];
35                 f[x+ln]=(f[x]-t+mod)%mod;
36                 f[x]=(t+f[x])%mod;
37                 if(v==-1) f[x]=f[x]*inv%mod,f[x+ln]=f[x+ln]*inv%mod;
38             }
39     }
40 }
41  
42 int main()
43 {
44     for (R i=2;i<=50000;++i)
45     {
46         if(!vis[i]) pri[++h]=i;
47         for (R j=1;j<=h&&i*pri[j]<=50000;++j)
48         {
49             vis[ i*pri[j] ]=1;
50             if(i%pri[j]==0) break;
51         }
52     }
53     while(scanf("%d%d",&n,&m)!=EOF)
54     {
55         memset(f,0,sizeof(f));
56         for (R i=1;i<=h;++i)
57             if(pri[i]<=m) f[ pri[i] ]++;
58         len=1; while(len<=m) len<<=1;
59         fwt(f,1);
60         for (R i=0;i<len;++i) f[i]=qui(f[i],n);
61         fwt(f,-1);
62         printf("%lld\n",f[0]);
63     }
64     return 0;
65 }

Hard Nim

　　「Binary Table」：https://codeforces.com/problemset/problem/662/C

　　题意概述：给定一个 $n\times m$ 的棋盘，上面有的写着1，有的写着0，每次可以翻转一行或一列，求最少可以剩下多少个一。$n<=20,m<=10^5$

　　两维范围差别这么大，看起来就像是要枚举其中一维了。枚举行的翻转情况，记为 $i$ ，此时每一列的情况就变成了 $i^x$.

　　总答案即为 $\sum min(siz[i\oplus x],n-siz[i\oplus x])$

　　$siz[ i\oplus x]$ 看起来有点难，能不能枚举 $i \oplus x$ 呢?

　　是可以的，答案就变成了：

　　$\sum_{i \oplus j=x} f[j] \times min(siz[i],n-siz[i])$

　　$f[j]$ 表示的是在整个网格中，状态 $j$ 出现了多少次。看起来已经非常接近 $fwt$ 了，最后再做一次变换就更明显了。定义 $g[i]$ 表示 $min(siz[i],n-siz[i])$ ：

　　$\sum_{i \oplus j=x} g[i]\times f[j]$

　　这样就可以用一遍 $fwt$ 算出所有 $x$ 的答案了。

 1 # include <cstdio>
 2 # include <iostream>
 3 # define R register int
 4 # define ll long long
 5 
 6 using namespace std;
 7 
 8 const int N=(1<<20)+5;
 9 const int M=100005;
10 int n,m,a[21][M],q,len;
11 ll f[N],g[N];
12 int b[M];
13 
14 void fwt (ll *f,int v)
15 {
16     for (R i=2;i<=len;i<<=1)
17     {
18         int ln=i>>1;
19         for (R b=0;b<len;b+=i)
20             for (R x=b;x<b+ln;++x)
21             {
22                 ll t=f[ln+x];
23                 f[ln+x]=f[x]-t;
24                 f[x]=f[x]+t;
25                 if(v==-1) f[ln+x]/=2,f[x]/=2;
26             }
27     }
28 }
29 
30 int main()
31 {
32     scanf("%d%d",&n,&m); len=1<<n;
33     q=(1<<n)-1;
34     for (R i=0;i<=q;++i) f[i]=f[i>>1]+(i&1);
35     for (R i=0;i<=q;++i) f[i]=min(f[i],n-f[i]);
36     for (R i=1;i<=n;++i)
37         for (R j=1;j<=m;++j)
38             scanf("%1d",&a[i][j]);
39     for (R i=1;i<=m;++i)
40         for (R j=1;j<=n;++j)
41             b[i]=b[i]*2+a[j][i];
42     for (R i=1;i<=m;++i) g[ b[i] ]++;
43     fwt(f,1); fwt(g,1);
44     for (R i=0;i<=q;++i) f[i]=f[i]*g[i];
45     fwt(f,-1);
46     ll ans=n*m;
47     for (R i=0;i<=q;++i) ans=min(ans,f[i]);
48     printf("%lld\n",ans);
49     return 0;
50 }

Binary Table

　　「排队」：https://www.lydsy.com/JudgeOnline/problem.php?id=2729

　　题意概述：n名男同学，m名女同学，两名老师排队，要求任意两名女同学不能相邻，老师不能相邻，求方案数。$n<=2000,m<=2000$

　　同时考虑两条限制比较复杂，先考虑一个。

　　首先将男生与老师排成一列，女生插空站，可以保证满足第一条，方案数：

　　$(n+2)!\times A_{n+3}^{m}$

　　再减去两个老师相邻的情况，可以用捆绑法来做，方案数：

　　$2\times (n+1)!\times A_{n+2}^m$

　　所以答案即为：

　　$(n+2)!\times A_{n+3}^{m}-2\times (n+1)!\times A_{n+2}^m$

　　看上去很简单呢！但当我开开心心地写完式子打算编程时，突然发现...没有取模，所以还得写高精度。

 1 # include <cstdio>
 2 # include <iostream>
 3 # include <cstring>
 4 # define R register int 
 5 
 6 using namespace std;
 7 
 8 const int maxn=2005;
 9 int a[100000],b[100000];
10 int n,m,f[100],t[maxn];
11 int ans;
12 
13 void add (int x,int v)
14 {
15     for (R i=2;i*i<=x;++i)
16     {
17         if(x%i) continue;
18         while(x%i==0) t[i]+=v,x/=i;
19     }
20     if(x!=1) t[x]+=v;
21 }
22 
23 void mul (int *a,int x)
24 {
25     int len=a[0]+4;
26     for (R i=1;i<=len;++i) a[i]*=x;
27     for (R i=1;i<=len;++i) a[i+1]+=a[i]/10,a[i]%=10;
28     while(a[len]==0&&len) len--;
29     a[0]=len;
30 }
31 
32 void write (int *a)
33 {
34     if(!a[0]) puts("0");
35     for (R i=a[0];i>=1;--i) printf("%d",a[i]);
36 }
37 
38 void sub (int *a,int *b)
39 {
40     int len=a[0];
41     for (R i=1;i<=len;++i)
42     {
43         a[i]-=b[i];
44         if(a[i]<0) a[i]+=10,a[i+1]--;
45     }
46     while(a[len]==0&&len) len--;
47     a[0]=len;
48 }
49 
50 int main()
51 {
52     scanf("%d%d",&n,&m);
53     if(n+3<m) { puts("0"); return 0; }
54     a[0]=a[1]=1;
55     for (R i=1;i<=n+2;++i) add(i,1);
56     for (R i=1;i<=n+3;++i) add(i,1);
57     for (R i=1;i<=n+3-m;++i) add(i,-1);
58     for (R i=2;i<=2000;++i)
59         for (R j=1;j<=t[i];++j)
60             mul(a,i);
61     if(n+2<m) { write(a); return 0; }
62     memset(t,0,sizeof(t));
63     b[0]=b[1]=1;
64     for (R i=1;i<=n+1;++i) add(i,1);
65     for (R i=1;i<=n+2;++i) add(i,1);
66     for (R i=1;i<=n+2-m;++i) add(i,-1);
67     t[2]++;
68     for (R i=2;i<=2000;++i)
69         for (R j=1;j<=t[i];++j)
70             mul(b,i);
71     sub(a,b);
72     write(a);
73     return 0;
74 }

排队

4.16：

　　「州区划分」：https://www.luogu.org/problemnew/show/P4221

　　题意概述：将一张 $n$ 个点的图分为 $k$ 部分，要求每部分满足某要求（反正是很容易预处理的那种，就不写了），每个划分方案的满意值为$\prod_{i=1}^k(\frac{\sum_{x\in V_i}w_x}{\sum_{j=1}^i\sum_{x\in V_j}w_x})^p$，求所有划分方案的满意值的和。$n<=21,p<=2$

　　这道题是状压dp，很显然吧。定义 $dp[i]$ 表示 $i$ 中的点已经规划完毕的满意值的和，枚举子集转移可以做到 $3^{21}$，会TLE。

　　仔细观察可以发现，这是一个子集卷积的形式，运用vfk在15年国家队论文里的思路，可以 $2^nn^2$ 解决（额外记录一维集合大小）

  1 # include <cstdio>
  2 # include <iostream>
  3 # include <cstring>
  4 # define R register int
  5 # define ll long long
  6  
  7 using namespace std;
  8 
  9 const int N=500;
 10 const int M=(1<<21)+5;
 11 const int mod=998244353;
 12 int n,m,p,q;
 13 int u[N],v[N],w[N],vis[N],d[N],fa[N],c[M];
 14 int s[M],f[22][M],g[22][M],h[22][M],inv[M],t[M],siz[M];
 15 
 16 int find (int x) { if(x==fa[x]) return x; return fa[x]=find(fa[x]); }
 17 
 18 bool check (int no)
 19 {
 20     for (R j=0;j<n;++j)
 21         if(no&(1<<j)) vis[j+1]=1; else vis[j+1]=0;
 22     for (R j=1;j<=n;++j)
 23         if(vis[j]==1) fa[j]=j;
 24     memset(d,0,sizeof(d));
 25     for (R j=1;j<=m;++j)
 26     {
 27         int x=u[j],y=v[j];
 28         if(vis[x]==0||vis[y]==0) continue;
 29         d[x]++; d[y]++;
 30         x=find(x); y=find(y);
 31         if(x!=y) fa[x]=y;
 32     }
 33     int zf=0,lt=1;
 34     for (R j=1;j<=n;++j)
 35     {
 36         if(!vis[j]) continue;
 37         fa[j]=find(fa[j]);
 38         if(!zf) zf=fa[j];
 39         if(fa[j]!=zf) lt=0;
 40     }
 41     if(!lt) return 1;
 42     int cnt=0;
 43     for (R j=1;j<=n;++j)
 44         if(d[j]&1) cnt++;
 45     if(cnt) return 1;
 46     return 0;
 47 }
 48 
 49 int ad (int a,int b) { a+=b; while(a>=mod) a-=mod; while(a<0) a+=mod; return a; }
 50 
 51 void fwt (int *f,int v)
 52 {
 53     for (R i=0;i<n;++i)
 54            for (R j=0;j<=q;++j)
 55                if(j&(1<<i)) f[j]=ad(f[j],v*f[j^(1<<i)]);
 56 }
 57 
 58 int qui (int a,int b)
 59 {
 60     int s=1;
 61     while(b)
 62     {
 63         if(b&1) s=1LL*s*a%mod;
 64         a=1LL*a*a%mod;
 65         b>>=1; 
 66     }
 67     return s;
 68 }
 69 
 70 int main()
 71 {
 72     scanf("%d%d%d",&n,&m,&p);
 73     for (R i=1;i<=m;++i) scanf("%d%d",&u[i],&v[i]);
 74     for (R i=0;i<n;++i) scanf("%d",&w[i]);
 75     q=(1<<n)-1;
 76     for (R i=0;i<=q;++i)
 77         for (R j=0;j<n;++j)
 78             if(i&(1<<j)) s[i]=ad(s[i],w[j]);
 79     for (R i=1;i<=q;++i)
 80         c[i]=check(i);
 81     for (R i=0;i<=q;++i)
 82         if(p==0) s[i]=1;
 83         else if(p==2) s[i]=1LL*s[i]*s[i]%mod;
 84     for (R i=0;i<=q;++i) siz[i]=siz[i>>1]+((i&1)?1:0);
 85     for (R i=0;i<=q;++i) inv[i]=qui(s[i],mod-2);
 86     memset(f,0,sizeof(f));
 87     f[0][0]=1;
 88     for (R i=0;i<=q;++i)
 89         if(c[i]) g[ siz[i] ][i]=s[i];
 90     for (R i=0;i<=n;++i) fwt(g[i],1);
 91     for (R i=1;i<=n;++i)
 92     {
 93         fwt(f[i-1],1);
 94         for (R j=0;j<i;++j)
 95             for (R s=0;s<=q;++s)
 96             {
 97                 if(f[j][s]==0) continue;
 98                 if(g[i-j][s]==0) continue;
 99                 f[i][s]=ad(f[i][s],1LL*f[j][s]*g[i-j][s]%mod);
100             }
101         fwt(f[i],-1);
102         for (R s=0;s<=q;++s)
103             if(siz[s]==i) f[i][s]=1LL*f[i][s]*inv[s]%mod;
104             else f[i][s]=0;
105     }
106     cout<<f[ siz[q] ][q];
107     return 0;
108 }

州区划分

　　「随机算法」：https://loj.ac/problem/2540

　　题意概述：小C使用如下方法寻找一张点数为 $n$ 的图的最大独立集：1.随机生成一个节点序号的排列；2.依次判断能否加进目前的独立集；问他成功的概率。$n<=20$

　　首先可以使用状压dp求出最大独立集的大小，但是其实没有必要...

　　这道题虽然是求概率，但是完全可以求出方案数后除以总方案数，所以还是一道计数题。

　　设置 $dp$ 状态：$dp[i]$ 表示，$i$ 这个集合已经被选中的方案数。仔细思考发现不行，还得考虑哪些点是已经试过但是没放进去的，这样状态数就变得有点大，跑不过去了。

　　来理理思路吧。有三种点：已经在独立集里的，还没考虑过的，考虑过但没放进独立集里的；只要想将这三种点区分开，无论如何复杂度也是降不下来的，能不能优化呢？

　　重新定义状态，改为：$dp[i][j]$ 表示当前最大独立集的大小为 $i$ ，$j$ 这个集合里的点不能再选的方案数。当加入一个点 $x$ 时，它周围的点就不能再选了，也一并加入，对这些点，唯一的要求是必须放在 $x$ 后面,转移如下：$dp[i+1][ j|c[k] ]+=dp[i][j] \times A_{n-siz[j]-1}^{siz[ c[k] ]-siz[ j\&c[k] ]-1}$

　　解释一下：首先 $c[k]$ 表示的是 $c$ 和与 $c$ 相连的点的集合。当加入一些点的时候，$k$ 必须被放到第一个有空位的地方，而其它点可以任选，即后面乘上的排列数。复杂度为 $n^22^n$ .

　　根据dp的最优子结构性，对于两个“已考虑集合”相同的状态，如果某一个的独立集比另一个小，那么它肯定不能转移到一个最终状态了，这样还可以再省掉一维，不过我没写。

 1 # include <cstdio>
 2 # include <iostream>
 3 # include <cstdlib>
 4 # define R register int
 5 
 6 using namespace std;
 7 
 8 const int maxn=(1<<20)+5;
 9 const int mod=998244353;
10 int n,m,q,x,y,maxs,ans;
11 int a[maxn],c[21],siz[maxn],vis[maxn],f[21],inv[21];
12 int dp[21][maxn];
13 
14 int qui (int a,int b)
15 {
16     int s=1;
17     while(b)
18     {
19         if(b&1) s=1LL*s*a%mod;
20         a=1LL*a*a%mod;
21         b>>=1;
22     }
23     return s;
24 }
25 
26 int A (int x,int y) { return 1LL*f[x]*inv[x-y]%mod; }
27 
28 int init()
29 {
30     for (R i=0;i<=q;++i)
31     {
32         if(!vis[i]) continue;
33         for (R j=1;j<=n;++j)
34         {
35             if(c[j]&i) continue;
36             vis[i|(1<<(j-1))]=1;
37         }
38     }
39     for (R i=0;i<=q;++i) if(vis[i]) maxs=max(maxs,siz[i]);
40     return maxs;
41 }
42 
43 int main()
44 {
45     scanf("%d%d",&n,&m);
46     f[0]=1; for (R i=1;i<=n;++i) f[i]=1LL*f[i-1]*i%mod;
47     inv[n]=qui(f[n],mod-2);
48     for (R i=n;i>=1;--i) inv[i-1]=1LL*inv[i]*i%mod;
49     vis[0]=1; q=(1<<n)-1;
50     for (R i=1;i<=n;++i) c[i]|=(1<<(i-1));
51     for (R i=1;i<=m;++i)
52     {
53         scanf("%d%d",&x,&y);
54         c[x]|=(1<<(y-1));
55         c[y]|=(1<<(x-1));
56     }
57     for (R i=0;i<=q;++i) siz[i]=siz[i>>1]+((i&1)?1:0);
58     maxs=init();
59     dp[0][0]=1;
60     for (R i=0;i<n;++i)
61         for (R j=0;j<=q;++j)
62         {
63             if(dp[i][j]==0) continue;
64             for (R k=1;k<=n;++k)
65             {
66                 if((1<<(k-1))&j) continue;
67                 int x=siz[j],y=siz[j|c[k]];
68                 dp[i+1][j|c[k]]=(dp[i+1][j|c[k]]+1LL*dp[i][j]*A(n-x-1,siz[ c[k] ]-siz[j&c[k]]-1))%mod;
69             }
70         }
71     ans=1LL*dp[maxs][q]*inv[n]%mod;
72     printf("%d\n",ans);
73     return 0;
74 }

随机算法

　　「随机游走」：https://loj.ac/problem/2542

　　自从开始准备省选，题目变得越来越难，完全独立做出来而且一遍A的题就越来越少啦。有时候会想一半，然后看看题解检查一下对不对，再往下写，但是这样不好，因为考场上没有人会让你看一看自己的算法对不对。R1D1T2 没做出来，其实就是很少独立做题，所以想出做法不敢写，写完了又怀疑对不对。最后出了考场发现其实就是细节问题，平时细节经常是对着题解改的，以后不能再这样了。不过这道题是自己做的~

　　题意概述：给定一棵树，从一个给定起点开始随机游走，$Q$ 组询问，每次给出一个集合，求期望多少步可以将这个集合里的点都走至少一次。$n<=18,q<=5000,\%998244353$

　　先想个暴力，模拟随机游走的过程，看看走多少次能达到要求的精度...竟然是对分数取模，不给暴力选手活路啊。

　　可以考虑设这么一个状态 $dp[i][j]$ 表示目前走到过的集合为 $i$ ，现在在 $j$ 的期望步数，它对吗？不知道，因为我直接放弃了这个做法。

　　至少一次是一个比较困难的条件，发现 $n$ 很小，可以用 $Min-Max$ 容斥来解决。转化为至少经过集合里的一个点的期望步数，这就好做多了。按照套路，设 $dp[i]$ 表示目前在 $i$ 这个点，期望还要走多少步才能经过任意一个集合里的点，边界条件就是集合里的点答案为0.发现两个点可以互相走来走去，所以列出每个点对其他点的贡献方程，高斯消元一下即可。这样做看起来复杂度上天，好像是 $2^nn^3$ 再乘一些常数，算一下发现是 $1e9$ 这个级别的，并不是特别大，好像还有优化的空间。

　　1、被选中集合里的点其实没有区别，将它们视为同一个，复杂度就变成了 $\sum_{i=1}^n\binom{n}{n-i}i^3$ ，用程序算一算发现大约是 $2e8$ 。

　　2、还要考虑的是有些点可能根本不会经过。如下图：粉色点为选中的集合，黄色点为起点，那么想要走到蓝色点，路上就会被粉色点拦住，所以根本没必要算它们的答案，又可以优化一些复杂度，虽然比较玄学，但是可能是有用的。

　　3、强行将起点的方程放到最后一行，消元后可以省略回代过程，理论上可以快一倍。

　　4、如果对于每次询问都暴力地做容斥，就有可能 $T$ ，可以在询问前先用高维前缀和处理所有答案，这样每次回答的复杂度就是 $O(1)$；

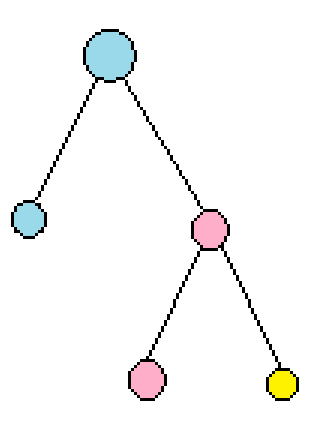
　　这样做就可以通过本题了。

  1 # include <cstdio>
  2 # include <iostream>
  3 # include <vector>
  4 # include <cstring>
  5 # define R register int
  6 
  7 using namespace std;
  8 
  9 const int maxn=(1<<18)+5;
 10 const int mod=998244353;
 11 int n,Q,x,k;
 12 int a,b,s,d[20],vis[20];
 13 int g[20][20],id[20];
 14 int ans[maxn],siz[maxn],tc[20];
 15 vector <int> v[20];
 16 
 17 int qui (int a,int b)
 18 {
 19     int s=1;
 20     while(b)
 21     {
 22         if(b&1) s=1LL*s*a%mod;
 23         a=1LL*a*a%mod;
 24         b>>=1;
 25     }
 26     return s;
 27 }
 28 
 29 int ad (int a,int b)
 30 {
 31     a+=b;
 32     while(a>=mod) a-=mod;
 33     while(a<0) a+=mod;
 34     return a;
 35 }
 36 
 37 int Gauss (int n)
 38 {
 39     int x;
 40     for (R i=1;i<=n;++i)
 41     {
 42         for (R j=i+1;j<=n;++j)
 43         {
 44             x=1LL*g[j][i]*qui(g[i][i],mod-2)%mod;
 45             x=mod-x;
 46             for (R k=i;k<=n+1;++k)
 47                 g[j][k]=ad(g[j][k],1LL*g[i][k]*x%mod);    
 48         }
 49     }
 50     return (1LL*g[n][n+1]*qui(g[n][n],mod-2)%mod+mod)%mod;
 51 }
 52 
 53 void dfs (int x)
 54 {
 55     if(tc[x]) return;
 56     tc[x]=1;
 57     if(vis[x]) return;
 58     int siz=v[x].size();
 59     for (R i=0;i<siz;++i)
 60         dfs(v[x][i]);
 61 }
 62 
 63 int cal (int s)
 64 {
 65     if(s&(1<<(x-1))) return 0;
 66     for (R i=1;i<=n;++i)
 67         if(s&(1<<(i-1))) vis[i]=1; else vis[i]=0;
 68     memset(tc,0,sizeof(tc));
 69     dfs(x);
 70     memset(g,0,sizeof(g));
 71     int cnt=0;
 72     for (R i=1;i<=n;++i)
 73         if(vis[i]==0&&i!=x&&tc[i]) id[i]=++cnt;
 74         else id[i]=0;
 75     id[x]=++cnt;
 76     for (R i=1;i<=n;++i)
 77     {
 78         if(vis[i]) continue;
 79         if(!tc[i]) continue;
 80         int siz=v[i].size();
 81         g[ id[i] ][ id[i] ]=1;
 82         for (R j=0;j<siz;++j)
 83         {
 84             int x=v[i][j];
 85             if(!id[x]) continue;
 86             g[ id[i] ][ id[x] ]=mod-d[i];
 87         }
 88         g[ id[i] ][cnt+1]=1;
 89     }
 90     return Gauss(cnt);
 91 }
 92 
 93 int main()
 94 {
 95     scanf("%d%d%d",&n,&Q,&x);
 96     for (R i=1;i<n;++i)
 97     {
 98         scanf("%d%d",&a,&b);
 99         d[a]++; d[b]++;
100         v[a].push_back(b);
101         v[b].push_back(a);
102     }
103     for (R i=1;i<=n;++i) d[i]=qui(d[i],mod-2);
104     int q=(1<<n)-1;
105     for (R i=1;i<=q;++i)
106         ans[i]=cal(i);
107     for (R i=1;i<=q;++i) siz[i]=siz[i>>1]+((i&1)?1:0);
108     for (R i=1;i<=q;++i)
109         if(siz[i]%2==0) ans[i]=(mod-ans[i])%mod;
110     for (R i=0;i<n;++i)
111         for (R j=0;j<=q;++j)
112             if(j&(1<<i))
113                 ans[j]=ad(ans[j],ans[j^(1<<i)]);
114     while(Q--)
115     {
116         scanf("%d",&k); s=0;
117         for (R i=1;i<=k;++i)
118             scanf("%d",&a),s|=(1<<(a-1));
119         printf("%d\n",ans[s]);
120     }
121     return 0;
122 }

随机游走-1

　　做完后发现这道题的正解不是这个。刚刚的做法完全没有利用到这是一棵树的性质...其实解方程部分可以不用高斯消元，而是手动优化这个过程，真的好奇妙。

　　设一个点的期望步数为 $E_x$ ，那么有 $E_x=\frac{1}{d_x}(E_f+\sum E_{son})+1$ ，设 $E_x=A_xE_f+B_x$ (怎么想到的),接下来是将式子化来化去的一番神仙操作：

　　$d_xE_x=E_f+\sum E_{son}+d_x$

　　$d_xE_x=E_f+\sum(A_{son}E_x+B_{son})+d_x$

　　$(d_x-\sum A_{son})E_x=E_f+\sum B_{son}+d_x$

　　$E_x=\frac{1}{d_x-\sum A_{son}}E_f+\frac{\sum B_{son}+d_x}{d_x-\sum A_{son}}$

　　$\therefore A_x=\frac{1}{d_x-\sum A_{son}} ,B_x=\frac{\sum B_{son}+d_x}{d_x-\sum A_{son}}$

　　边界情况：叶子节点没有儿子，集合里的点两个参数都为0;因为是无根树，将起点钦定为树根，就没有父亲的贡献，答案即为$B_x$

　　复杂度 $O(2^nn)$. 其实也并没有快多少...倒是短了挺多。

 1 # include <cstdio>
 2 # include <iostream>
 3 # include <vector>
 4 # include <cstring>
 5 # define R register int
 6 
 7 using namespace std;
 8 
 9 const int maxn=(1<<18)+5;
10 const int mod=998244353;
11 int n,Q,x,k;
12 int a,b,s,d[20],vis[20];
13 int g[20][20],id[20],A[20],B[20];
14 int ans[maxn],siz[maxn],tc[20];
15 vector <int> v[20];
16 
17 int qui (int a,int b)
18 {
19     int s=1;
20     while(b)
21     {
22         if(b&1) s=1LL*s*a%mod;
23         a=1LL*a*a%mod;
24         b>>=1;
25     }
26     return s;
27 }
28 
29 int ad (int a,int b)
30 {
31     a+=b;
32     while(a>=mod) a-=mod;
33     while(a<0) a+=mod;
34     return a;
35 }
36 
37 void dfs (int x)
38 {
39     tc[x]=1;
40     if(vis[x]) { A[x]=B[x]=0; return; }
41     int j,siz=v[x].size();
42     A[x]=d[x],B[x]=d[x];
43     for (R i=0;i<siz;++i)
44     {
45         j=v[x][i];
46         if(tc[j]) continue;
47         dfs(j);
48         A[x]=ad(A[x],-A[j]);
49         B[x]=ad(B[x],B[j]);
50     }
51     A[x]=qui(A[x],mod-2);
52     B[x]=1LL*A[x]*B[x]%mod;
53 }
54 
55 int cal (int s)
56 {
57     if(s&(1<<(x-1))) return 0;
58     for (R i=1;i<=n;++i)
59         if(s&(1<<(i-1))) vis[i]=1; else vis[i]=0;
60     memset(tc,0,sizeof(tc));
61     dfs(x);
62     return B[x];
63 }
64 
65 int main()
66 {
67     scanf("%d%d%d",&n,&Q,&x);
68     for (R i=1;i<n;++i)
69     {
70         scanf("%d%d",&a,&b);
71         d[a]++; d[b]++;
72         v[a].push_back(b);
73         v[b].push_back(a);
74     }
75     int q=(1<<n)-1;
76     for (R i=1;i<=q;++i)
77         ans[i]=cal(i);
78     for (R i=1;i<=q;++i) siz[i]=siz[i>>1]+((i&1)?1:0);
79     for (R i=1;i<=q;++i)
80         if(siz[i]%2==0) ans[i]=(mod-ans[i])%mod;
81     for (R i=0;i<n;++i)
82         for (R j=0;j<=q;++j)
83             if(j&(1<<i))
84                 ans[j]=ad(ans[j],ans[j^(1<<i)]);
85     while(Q--)
86     {
87         scanf("%d",&k); s=0;
88         for (R i=1;i<=k;++i)
89             scanf("%d",&a),s|=(1<<(a-1));
90         printf("%d\n",ans[s]);
91     }
92     return 0;
93 }

随机游走-2

　　「旅行者」：https://loj.ac/problem/3087

　　题意概述：给出一张 $n$ 个点 $m$ 条边的有向图，$k$ 个特殊点，求任意两个特殊点间的最短路的最小值。$n<=10^5,m<=5\times 10^5$

　　对这个题有点印象，可能shallwe学长讲过吧。

　　考虑一个弱化版本：给出两个集合 $A$,$B$ 求两个集合间的最短路；建立超级源汇，分别向A，B连边权为0的边，正反跑两遍最短路即可。

　　那么对于这道题，只要找到一种合理的拆分方法，使得任意点对都被拆开即可...根本不可能嘛...所以肯定是要拆好几次了。将所有特殊点用二进制表示，对于不同的两个点，在二进制表示下至少有一位是不一样的，所以对于每一位分别做，根据01分组跑多源多汇最短路。注意：因为这道题是有向图，所以不要忘了从0到1和从1到0各跑一遍。

　　网上还有一个做法是记录离每条边两端最近的特殊点，可以过，但是我认为可能还得记录次近点。有没有神仙可以给我讲一讲啊。

  1 # include <cstdio>
  2 # include <iostream>
  3 # include <cstring>
  4 # include <queue>
  5 # define R register int
  6 # define ll long long
  7 # define pac(a,b) make_pair(a,b)
  8 # define getchar() (S==TT&&(TT=(S=BB)+fread(BB,1,1<<20,stdin),S==TT)?EOF:*S++)
  9 
 10 using namespace std;
 11 
 12 const int maxn=700005;
 13 const ll inf=1e17;
 14 int T,n,m,k,s,t,u,v,z,a[maxn];
 15 int firs[maxn],h,th,vis[maxn];
 16 ll d[maxn];
 17 char BB[1 << 20], *S = BB, *TT = BB; 
 18 struct edge { int too,nex; ll z; }g[maxn<<1];
 19 typedef pair<ll,int> pii;
 20 priority_queue <pii,vector<pii>,greater<pii> >q;
 21 
 22 void add (int x,int y,ll z)
 23 {
 24     g[++h].nex=firs[x];
 25     firs[x]=h;
 26     g[h].too=y;
 27     g[h].z=z;
 28 }
 29 
 30 ll dij()
 31 {
 32     for (R i=1;i<=n+2;++i) d[i]=inf;
 33     memset(vis,0,sizeof(vis));
 34     d[s]=0; q.push(pac(0,s));
 35     int beg,j;
 36     while(q.size())
 37     {
 38         beg=q.top().second;
 39         q.pop();
 40         if(vis[beg]) continue;
 41         vis[beg]=1;
 42         for (R i=firs[beg];i;i=g[i].nex)
 43         {
 44             j=g[i].too;
 45             if(d[beg]+g[i].z>=d[j]) continue;
 46             d[j]=d[beg]+g[i].z;
 47             q.push(pac(d[j],j));
 48         }
 49     }
 50     return d[t];
 51 }
 52 
 53 ll cal (int x,int v)
 54 {
 55     int th=h;
 56     for (R i=1;i<=k;++i)
 57         if((a[i]&(1<<x))==v) add(a[i],t,0);
 58         else add(s,a[i],0);
 59     ll ans=dij();
 60     h=th;
 61     firs[s]=0;
 62     for (R i=1;i<=k;++i)
 63         if((a[i]&(1<<x))==v)
 64             firs[ a[i] ]=g[ firs[ a[i] ] ].nex; 
 65     return ans;
 66 }
 67 
 68 inline int read()
 69 {
 70     R x=0;
 71     char c=getchar();
 72     while (!isdigit(c)) c=getchar();
 73     while (isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar();
 74     return x;
 75 }
 76 
 77 int main()
 78 {
 79     scanf("%d",&T);
 80     while(T--)
 81     {
 82         n=read(),m=read(),k=read();
 83         s=n+1,t=n+2;
 84         memset(firs,0,sizeof(firs)); h=0;
 85         for (R i=1;i<=m;++i)
 86         {
 87             u=read(),v=read(),z=read();
 88             add(u,v,z);
 89         }
 90         for (R i=1;i<=k;++i)
 91             a[i]=read();
 92         ll ans=inf;
 93         for (R i=0;i<=16;++i)
 94         {
 95             if((1<<i)>n) break;
 96             ans=min(ans,min(cal(i,0),cal(i,1<<i)));
 97         }
 98         printf("%lld\n",ans);
 99     }
100     return 0;
101 }

旅行者

4.17：

　　「旧词」：https://loj.ac/problem/3088

　　题意概述：给定点数 $n$ 的一棵有根树，$q$ 次询问，每次给出 $x,y$ ，询问 $\sum\limits_{i=1}^xdep(lca(i,y))^k$.$n,q<=5\times 10^4$

　　对于任意一组询问，LCA只可能是y的祖先们，且如果一个 $x$ 点与 $y$ 的 $LCA$ 是 $k$ ，那么 $x$ 就一定在 $k$ 的子树内。但反过来却不成立，$x$ 即使在k的子树内,LCA也可能不是k,这怎么办呢？如果一个点在 $k$ 的子树内，且 $LCA$ 不是它，那么这个点肯定也在 $k$　往 $y$ 方向上儿子的子树内。因为找儿子比较麻烦,所以这部分多算的贡献不如从那个儿子处减掉。因此，我们可以推算出每个点的子树内的点对答案的贡献是多少，即 $dep[x]^k-(dep[x]-1)^k$.

　　问题在于我们不能快速的将一堆点全部塞入这个体系，如果对于每个询问都暴力插入 $x$ 又太慢了。刚刚的做法给了我们启发，每个点的贡献是不变的，所以我们可以同时处理出所有 $y$ 的答案。分析到这里方法就很明晰了:按照 $x$ 对询问离线，用线段树+树剖动态维护每个点的答案，每加入一个点，就将从它到根上的每一个点贡献系数+1，查询时则查询 $y$ 到根路径上每个点答案的和。

  1 /* shzr */
  2 # include <cstdio>
  3 # include <iostream>
  4 # include <algorithm>
  5 # define R register int
  6 # define nl (n<<1)
  7 # define nr (n<<1|1)
  8 
  9 using namespace std;
 10 
 11 const int maxn=50004;
 12 const int mod=998244353;
 13 int n,q,K,f[maxn],x,y,dk[maxn],siz[maxn];
 14 int h,firs[maxn],dep[maxn],v[maxn],cnt;
 15 int t[maxn<<2],k[maxn<<2],delta[maxn<<2],id[maxn],nid[maxn];
 16 int Top[maxn],son[maxn],ans[maxn];
 17 struct edge { int too,nex; }g[maxn<<1];
 18 struct ask { int x,y,id; }s[maxn];
 19 
 20 void add (int x,int y)
 21 {
 22     g[++h].nex=firs[x];
 23     firs[x]=h;
 24     g[h].too=y;
 25 }
 26 
 27 int qui (int a,int b)
 28 {
 29     int s=1;
 30     while(b)
 31     {
 32         if(b&1) s=1LL*s*a%mod;
 33         a=1LL*a*a%mod;
 34         b>>=1;
 35     }
 36     return s;
 37 }
 38 
 39 void pushdown (int n)
 40 {
 41     int x=delta[n]; delta[n]=0;
 42     t[nl]=(t[nl]+1LL*x*k[nl])%mod;
 43     t[nr]=(t[nr]+1LL*x*k[nr])%mod;
 44     delta[nl]=(delta[nl]+x)%mod;
 45     delta[nr]=(delta[nr]+x)%mod;
 46 }
 47 
 48 void dfs (int x)
 49 {
 50     int j,maxs=-1; siz[x]=1;
 51     for (R i=firs[x];i;i=g[i].nex)
 52     {
 53         j=g[i].too;
 54         if(dep[j]) continue;
 55         dep[j]=dep[x]+1;
 56         dfs(j);
 57         siz[x]+=siz[j];
 58         if(siz[j]>=maxs) son[x]=j,maxs=siz[j];
 59     }
 60 }
 61 
 62 void dfs2 (int x,int Tp)
 63 {
 64     Top[x]=Tp; id[x]=++cnt; nid[cnt]=x;
 65     if(!son[x]) return;
 66     dfs2(son[x],Tp);
 67     int j;
 68     for (R i=firs[x];i;i=g[i].nex)
 69     {
 70         j=g[i].too;
 71         if(j==son[x]||j==f[x]) continue;
 72         dfs2(j,j);
 73     }
 74 }
 75 
 76 bool cmp (ask a,ask b) { return a.x<b.x; }
 77 
 78 int ad (int x,int y)
 79 {
 80     x+=y;
 81     if(x>=mod) x-=mod;
 82     return x;
 83 }
 84 
 85 void build (int n,int l,int r)
 86 {
 87     if(l==r)
 88     {
 89         k[n]=v[ nid[l] ];
 90         t[n]=delta[n]=0;
 91         return;
 92     }
 93     int mid=(l+r)>>1;
 94     build(nl,l,mid);
 95     build(nr,mid+1,r);
 96     t[n]=ad(t[nl],t[nr]);
 97     k[n]=ad(k[nl],k[nr]);
 98 }
 99 
100 int ask (int n,int l,int r,int ll,int rr)
101 {
102     if(ll<=l&&r<=rr) return t[n];
103     int mid=(l+r)>>1,ans=0;
104     if(delta[n]) pushdown(n);
105     if(ll<=mid) ans=ask(nl,l,mid,ll,rr);
106     if(rr>mid) ans=ad(ans,ask(nr,mid+1,r,ll,rr));
107     return ans;
108 }
109 
110 void add (int n,int l,int r,int ll,int rr)
111 {
112     if(ll<=l&&r<=rr)
113     {
114         t[n]=ad(t[n],k[n]);
115         delta[n]=ad(delta[n],1);
116         return;
117     }
118     int mid=(l+r)>>1;
119     if(delta[n]) pushdown(n);
120     if(ll<=mid) add(nl,l,mid,ll,rr);
121     if(rr>mid) add(nr,mid+1,r,ll,rr);
122     t[n]=ad(t[nl],t[nr]);
123 }
124 
125 void add_t (int x,int y)
126 {
127     while(Top[x]!=Top[y])
128     {
129         if(dep[ Top[x] ]>dep[ Top[y] ]) swap(x,y);
130         add(1,1,n,id[ Top[y] ],id[y]);
131         y=f[ Top[y] ];
132     }
133     if(dep[x]>dep[y]) swap(x,y);
134     add(1,1,n,id[x],id[y]);
135 }
136 
137 int ask_t (int x,int y)
138 {
139     int ans=0;
140     while(Top[x]!=Top[y])
141     {
142         if(dep[ Top[x] ]>dep[ Top[y] ]) swap(x,y);
143         ans=ad(ans,ask(1,1,n,id[ Top[y] ],id[y]));
144         y=f[ Top[y] ];
145     }
146     if(dep[x]>dep[y]) swap(x,y);
147     ans=ad(ans,ask(1,1,n,id[x],id[y]));
148     return ans;
149 }
150 
151 int main()
152 {
153     scanf("%d%d%d",&n,&q,&K);
154     for (R i=2;i<=n;++i)
155     {
156         scanf("%d",&f[i]);
157         add(f[i],i);
158     }
159     dep[1]=1;
160     dfs(1);
161     dfs2(1,1);
162     for (R i=1;i<=n;++i) dk[i]=qui(dep[i],K);
163     for (R i=1;i<=n;++i) v[i]=(dk[i]-dk[ f[i] ]+mod)%mod;
164     for (R i=1;i<=q;++i)
165     {
166         scanf("%d%d",&s[i].x,&s[i].y);
167         s[i].id=i;
168     }
169     sort(s+1,s+1+q,cmp);
170     build(1,1,n);
171     int l=1;
172     for (R i=1;i<=q;++i)
173     {
174         while(l<=s[i].x&&l<=n) add_t(1,l),l++;
175         ans[ s[i].id ]=ask_t(1,s[i].y);
176     }
177     for (R i=1;i<=q;++i)
178         printf("%d\n",ans[i]);
179     return 0;
180 }

旧词

　　「LCA」：https://www.lydsy.com/JudgeOnline/problem.php?id=3626

　　和上个题差不多，虽然询问变成了一个区间，但是拆成两个询问做个差也就没区别了。

  1 # include <cstdio>
  2 # include <iostream>
  3 # include <algorithm>
  4 # define R register int
  5 # define nl (n<<1)
  6 # define nr (n<<1|1)
  7  
  8 using namespace std;
  9  
 10 const int maxn=50004;
 11 const int mod=201314;
 12 int n,q,K,f[maxn],x,y,siz[maxn];
 13 int h,firs[maxn],dep[maxn],cnt;
 14 int t[maxn<<2],k[maxn<<2],delta[maxn<<2],id[maxn];
 15 int Top[maxn],son[maxn],ans[maxn];
 16 struct edge { int too,nex; }g[maxn<<1];
 17 struct ask { int x,y,id,v; }a[maxn<<1];
 18  
 19 void add (int x,int y)
 20 {
 21     g[++h].nex=firs[x];
 22     firs[x]=h;
 23     g[h].too=y;
 24 }
 25  
 26 void pushdown (int n)
 27 {
 28     int x=delta[n]; delta[n]=0;
 29     t[nl]=(t[nl]+1LL*x*k[nl])%mod;
 30     t[nr]=(t[nr]+1LL*x*k[nr])%mod;
 31     delta[nl]=(delta[nl]+x)%mod;
 32     delta[nr]=(delta[nr]+x)%mod;
 33 }
 34  
 35 void dfs (int x)
 36 {
 37     int j,maxs=-1; siz[x]=1;
 38     for (R i=firs[x];i;i=g[i].nex)
 39     {
 40         j=g[i].too;
 41         if(dep[j]) continue;
 42         dep[j]=dep[x]+1;
 43         dfs(j);
 44         siz[x]+=siz[j];
 45         if(siz[j]>=maxs) son[x]=j,maxs=siz[j];
 46     }
 47 }
 48  
 49 void dfs2 (int x,int Tp)
 50 {
 51     Top[x]=Tp; id[x]=++cnt;
 52     if(!son[x]) return;
 53     dfs2(son[x],Tp);
 54     int j;
 55     for (R i=firs[x];i;i=g[i].nex)
 56     {
 57         j=g[i].too;
 58         if(j==son[x]||j==f[x]) continue;
 59         dfs2(j,j);
 60     }
 61 }
 62  
 63 bool cmp (ask a,ask b) { return a.x<b.x; }
 64  
 65 int ad (int x,int y)
 66 {
 67     x+=y;
 68     if(x>=mod) x-=mod;
 69     return x;
 70 }
 71  
 72 void build (int n,int l,int r)
 73 {
 74     if(l==r)
 75     {
 76         k[n]=1;
 77         t[n]=delta[n]=0;
 78         return;
 79     }
 80     int mid=(l+r)>>1;
 81     build(nl,l,mid);
 82     build(nr,mid+1,r);
 83     t[n]=ad(t[nl],t[nr]);
 84     k[n]=ad(k[nl],k[nr]);
 85 }
 86  
 87 int ask (int n,int l,int r,int ll,int rr)
 88 {
 89     if(ll<=l&&r<=rr) return t[n];
 90     int mid=(l+r)>>1,ans=0;
 91     if(delta[n]) pushdown(n);
 92     if(ll<=mid) ans=ask(nl,l,mid,ll,rr);
 93     if(rr>mid) ans=ad(ans,ask(nr,mid+1,r,ll,rr));
 94     return ans;
 95 }
 96  
 97 void add (int n,int l,int r,int ll,int rr)
 98 {
 99     if(ll<=l&&r<=rr)
100     {
101         t[n]=ad(t[n],k[n]);
102         delta[n]=ad(delta[n],1);
103         return;
104     }
105     int mid=(l+r)>>1;
106     if(delta[n]) pushdown(n);
107     if(ll<=mid) add(nl,l,mid,ll,rr);
108     if(rr>mid) add(nr,mid+1,r,ll,rr);
109     t[n]=ad(t[nl],t[nr]);
110 }
111  
112 void add_t (int x,int y)
113 {
114     while(Top[x]!=Top[y])
115     {
116         if(dep[ Top[x] ]>dep[ Top[y] ]) swap(x,y);
117         add(1,1,n,id[ Top[y] ],id[y]);
118         y=f[ Top[y] ];
119     }
120     if(dep[x]>dep[y]) swap(x,y);
121     add(1,1,n,id[x],id[y]);
122 }
123  
124 int ask_t (int x,int y)
125 {
126     int ans=0;
127     while(Top[x]!=Top[y])
128     {
129         if(dep[ Top[x] ]>dep[ Top[y] ]) swap(x,y);
130         ans=ad(ans,ask(1,1,n,id[ Top[y] ],id[y]));
131         y=f[ Top[y] ];
132     }
133     if(dep[x]>dep[y]) swap(x,y);
134     ans=ad(ans,ask(1,1,n,id[x],id[y]));
135     return ans;
136 }
137  
138 int main()
139 {
140     scanf("%d%d",&n,&q);
141     for (R i=2;i<=n;++i)
142     {
143         scanf("%d",&f[i]);
144         f[i]++;
145         add(f[i],i);
146     }
147     dep[1]=1;
148     dfs(1);
149     dfs2(1,1);
150     int cnt=0,l,r,y;
151     for (R i=1;i<=q;++i)
152     {
153         scanf("%d%d%d",&l,&r,&y);
154         l++; r++; y++;
155         a[++cnt].x=l-1,a[cnt].y=y,a[cnt].id=i,a[cnt].v=-1;
156         a[++cnt].x=r,a[cnt].y=y,a[cnt].id=i,a[cnt].v=1;
157     }
158     sort(a+1,a+1+cnt,cmp);
159     build(1,1,n);
160     int p=1;
161     for (R i=1;i<=cnt;++i)
162     {
163         while(p<=a[i].x&&p<=n) add_t(1,p),p++;
164         ans[ a[i].id ]=(ans[ a[i].id ]+a[i].v*ask_t(1,a[i].y)%mod+mod)%mod;
165     }
166     for (R i=1;i<=q;++i)
167         printf("%d\n",ans[i]);
168     return 0;
169 }

LCA

　　「与或和」：https://loj.ac/problem/3083

　　题意概述：给定一个 $n\times n$ 的矩阵，希望求出所有子矩阵的 $and$ 和的算术和，以及 $or$ 和的算术和。$n<=1000$

　　这种题我还能出好多：子矩阵 $and$ 和的 $and$ 和， $or$ 和的 $or$ 和， $xor$ 和的 $xor$ 和，算数和的算数和；

　　位运算各位之间互不影响，所以拆位做。

　　首先考虑 $and$ 和，发现只有全 $1$ 子矩阵的 $and$ 和为 $1$ ，其它子矩阵的 $and$ 和均为 $0$；

　　对于 $or$ 和，其实也类似，全 $0$ 子矩阵的 $or$ 和为 $0$，其它子矩阵的 $or$ 和均为 $1$。

　　这两个问题差不多，所以一起说。

　　枚举矩形的上边界，对于每个点，可以很容易的算出它往下最多可以延伸多少。再观察一下，发现以这个高度为上边界的全 $0$ 子矩形个数恰好为这一行所有子区间的最小值之和。这不就是“差异”吗？

  1 # include <cstdio>
  2 # include <iostream>
  3 # include <cstring>
  4 # define R register int
  5 # define ll long long
  6 
  7 using namespace std;
  8 
  9 const int maxn=1003;
 10 const int mod=1000000007;
 11 int n,s[maxn][maxn],m;
 12 int a[maxn][maxn],d[maxn][maxn];
 13 int sta[maxn],tp,l[maxn],r[maxn];
 14 ll ans1,ans2,S;
 15 
 16 int read()
 17 {
 18     R x=0;
 19     char c=getchar();
 20     while (!isdigit(c)) c=getchar();
 21     while (isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar();
 22     return x;
 23 }
 24 
 25 int ad (int a,int b)
 26 {
 27     a+=b;
 28     if(a>=mod) a-=mod;
 29     return a;
 30 }
 31 
 32 ll cal (int *f)
 33 {
 34     ll ans=0;
 35     tp=0;
 36     for (R i=1;i<=n;++i)
 37     {
 38         while(tp&&f[i]<f[ sta[tp] ])
 39         {
 40             r[ sta[tp] ]=i-1;
 41             tp--;
 42         }
 43         sta[++tp]=i;
 44     }
 45     for (R i=1;i<=tp;++i) r[ sta[i] ]=n;
 46     tp=0;
 47     for (R i=n;i>=1;--i)
 48     {
 49         while(tp&&f[i]<=f[ sta[tp] ])
 50         {
 51             l[ sta[tp] ]=i+1;
 52             tp--;
 53         }
 54         sta[++tp]=i;
 55     }
 56     for (R i=1;i<=tp;++i) l[ sta[i] ]=1;
 57     for (R i=1;i<=n;++i)
 58         ans=ad(ans,1LL*(i-l[i]+1)*(r[i]-i+1)%mod*f[i]%mod);
 59     return ans;
 60 }
 61 
 62 void ask (int v)
 63 {
 64     ll cnt=0;
 65     memset(d,0,sizeof(d));
 66     for (R i=n;i>=1;--i)
 67         for (R j=1;j<=n;++j)
 68             if(a[i][j]==1)
 69                 d[i][j]=d[i+1][j]+1;
 70     for (R i=1;i<=n;++i)
 71         cnt=ad(cnt,cal(d[i]));
 72     ans1=(ans1+cnt*v)%mod;
 73     cnt=0;
 74     memset(d,0,sizeof(d));
 75     for (R i=n;i>=1;--i)
 76         for (R j=1;j<=n;++j)
 77             if(a[i][j]==0)
 78                 d[i][j]=d[i+1][j]+1;
 79     for (R i=1;i<=n;++i)
 80         cnt=ad(cnt,cal(d[i]));
 81     ans2=(ans2+(S-cnt+mod)*v%mod)%mod;
 82 }
 83 
 84 int main()
 85 {
 86     n=read();
 87     for (R i=1;i<=n;++i)
 88         for (R j=1;j<=n;++j)
 89             s[i][j]=read(),m=max(m,s[i][j]);
 90     S=n*(n+1)/2; S=S*S;
 91     S=S%mod;
 92     for (R w=0;w<=30;++w)
 93     {
 94         if((1<<w)>m) break;
 95         for (R i=1;i<=n;++i)
 96             for (R j=1;j<=n;++j)
 97                 a[i][j]=(s[i][j]&(1<<w))?1:0;
 98         ask(1<<w);
 99     }
100     printf("%lld %lld",ans1,ans2);
101     return 0;
102 }

与或和

　　「树的同构」：https://www.luogu.org/problemnew/show/P5043

 1 // luogu-judger-enable-o2
 2 # include <cstdio>
 3 # include <iostream>
 4 # include <map>
 5 # include <cstring>
 6 # include <algorithm>
 7 # define R register int
 8 # define ULL unsigned long long
 9 
10 using namespace std;
11 
12 const int maxn=102;
13 const int base=233;
14 int n,m,siz[maxn],f,rt,h,firs[maxn],dep[maxn];
15 ULL a[maxn][maxn],Hash[maxn];
16 map <ULL,int> M;
17 struct edge { int too,nex; }g[maxn<<1];
18 
19 bool cmp (ULL a,ULL b) { return a>b; }
20 
21 void add (int x,int y)
22 {
23     g[++h].nex=firs[x];
24     firs[x]=h;
25     g[h].too=y;
26 }
27 
28 ULL dfs (int x)
29 {
30     siz[x]=1;
31     int tp=0,j;
32     for (R i=firs[x];i;i=g[i].nex)
33     {
34         j=g[i].too;
35         if(dep[j]) continue;
36         dep[j]=dep[x]+1;
37         a[x][++tp]=dfs(j);
38         siz[x]+=siz[j];
39     }
40     sort(a[x]+1,a[x]+1+tp,cmp);
41     ULL h=siz[x];
42     for (R i=1;i<=tp;++i)
43         h=h*base+a[x][i];
44     return h;
45 }
46 
47 int main()
48 {
49     scanf("%d",&m);
50     for (R i=1;i<=m;++i)
51     {
52         scanf("%d",&n);
53         int ans=i;
54         h=0; memset(firs,0,sizeof(firs));
55         for (R j=1;j<=n;++j)
56         {
57             scanf("%d",&f);
58             if(f) add(j,f),add(f,j);
59         }
60         for (R j=1;j<=n;++j)
61         {
62             memset(dep,0,sizeof(dep));
63             dep[j]=1;
64             ULL no=dfs(j);
65             if(!M[no]) M[no]=i;
66             ans=min(ans,M[no]);
67         }
68         printf("%d\n",ans);
69     }
70     return 0;
71 }

树的同构

  1 # include <cstdio>
  2 # include <iostream>
  3 # include <set>
  4 # include <cstring>
  5 # define R register int
  6 # define ULL unsigned long long
  7  
  8 using namespace std;
  9  
 10 const int maxn=100005;
 11 const ULL base1=1e5+9;
 12 const ULL base2=1e5+7;
 13 const ULL base3=709;
 14 int n,h,firs[maxn],siz[maxn],dep[maxn],f[maxn],x,y,d[maxn];
 15 ULL a[maxn];
 16 struct edge { int too,nex; }g[maxn<<1];
 17 set <ULL> s;
 18  
 19 void add (int x,int y)
 20 {
 21     g[++h].nex=firs[x];
 22     firs[x]=h;
 23     g[h].too=y;
 24 }
 25  
 26 void dfs1 (int x)
 27 {
 28     int j; siz[x]=1;
 29     a[x]=0;
 30     for (R i=firs[x];i;i=g[i].nex)
 31     {
 32         j=g[i].too;
 33         if(dep[j]) continue;
 34         dep[j]=dep[x]+1;
 35         dfs1(j);
 36         siz[x]+=siz[j];
 37         a[x]^=(a[j]*base1+base2);
 38     }
 39     a[x]^=(siz[x]+base3);
 40 }
 41  
 42 void dfs2 (int x)
 43 {
 44     int j;
 45     ULL T=a[x];
 46     for (R i=firs[x];i;i=g[i].nex)
 47     {
 48         j=g[i].too;
 49         if(dep[j]<dep[x]) continue;        
 50         T=a[x]^(a[j]*base1+base2);
 51         T^=(n+base3);
 52         T^=(n-siz[j]+base3);
 53         a[j]^=(T*base1+base2);
 54         a[j]^=(siz[j]+base3)^(n+base3);
 55         dfs2(j);
 56     }
 57 }
 58  
 59 bool check (int x)
 60 {
 61     int j;
 62     ULL T=0;
 63     for (R i=firs[x];i;i=g[i].nex)
 64     {
 65         j=g[i].too;
 66         T=a[j]^(base1*(1+base3)+base2);
 67         T^=(n+base3);
 68         T^=(n-1+base3);
 69     }
 70     if(s.find(T)!=s.end()) return 1;
 71     return 0;
 72 }
 73  
 74 int main()
 75 {
 76     scanf("%d",&n);
 77     for (R i=1;i<n;++i)
 78     {
 79         scanf("%d%d",&x,&y);
 80         add(x,y),add(y,x);
 81     }
 82     memset(dep,0,sizeof(dep));
 83     dep[1]=1;
 84     dfs1(1);
 85     dfs2(1);
 86     for (R i=1;i<=n;++i)
 87         s.insert(a[i]);
 88     h=0; memset(firs,0,sizeof(firs));
 89     n++;
 90     for (R i=1;i<n;++i)
 91     {
 92         scanf("%d%d",&x,&y);
 93         add(x,y); add(y,x);
 94         d[x]++; d[y]++;
 95     }
 96     memset(dep,0,sizeof(dep));
 97     dep[1]=1;
 98     dfs1(1);
 99     dfs2(1);
100     for (R i=1;i<=n;++i)
101     {
102         if(d[i]>1) continue;
103         if(check(i)) { printf("%d\n",i); break; }
104     }
105     return 0;
106 }

独特的树叶

 1 // luogu-judger-enable-o2
 2 # include <cstdio>
 3 # include <iostream>
 4 # include <cstring>
 5 # define R register int
 6 
 7 using namespace std;
 8 
 9 const int N=20;
10 const int mod=1e9+7;
11 int n,m[N];
12 int x[N][N*N],y[N][N*N];
13 int a[N][N],siz[(1<<N)+5];
14 int ans=0;
15 
16 int ad (int a,int b)
17 {
18     a+=b;
19     while(a>=mod) a-=mod;
20     while(a<0) a+=mod;
21     return a;
22 }
23 
24 int qui (int a,int b)
25 {
26     int s=1;
27     while(b)
28     {
29         if(b&1) s=1LL*s*a%mod;
30         a=1LL*a*a%mod;
31         b>>=1;
32     }
33     return s;
34 }
35 
36 int Gauss (int n)
37 {
38     int ans=1,t,x;
39     for (R i=1;i<=n;++i)
40     {
41         t=i;
42         for (R j=i;j<=n;++j)
43             if(a[j][i]>a[t][i]) t=j;
44         if(t!=i) swap(a[t],a[i]),ans=mod-ans;
45         for (R j=i+1;j<=n;++j)
46         {
47             x=1LL*a[j][i]*qui(a[i][i],mod-2)%mod;
48             for (R k=i;k<=n;++k)
49                 a[j][k]=ad(a[j][k],-1LL*a[i][k]*x%mod);
50         }
51         ans=1LL*ans*a[i][i]%mod;
52     }
53     return ans%mod;
54 }
55 
56 int cal (int s)
57 {
58     memset(a,0,sizeof(a));
59     for (R i=1;i<=n-1;++i)
60         if(s&(1<<(i-1)))
61             for (R j=1;j<=m[i];++j)
62             {
63                 a[ x[i][j] ][ x[i][j] ]++;
64                 a[ y[i][j] ][ y[i][j] ]++;
65                 a[ x[i][j] ][ y[i][j] ]--;
66                 a[ y[i][j] ][ x[i][j] ]--;
67             }
68     for (R i=1;i<=n;++i)
69         for (R j=1;j<=n;++j)
70             a[i][j]=ad(a[i][j],0);
71     return Gauss(n-1);
72 }
73 
74 int main()
75 {
76     scanf("%d",&n);
77     for (R i=1;i<n;++i)
78     {
79         scanf("%d",&m[i]);
80         for (R j=1;j<=m[i];++j)
81             scanf("%d%d",&x[i][j],&y[i][j]);
82     }
83     int q=(1<<(n-1))-1;
84     for (R i=1;i<=q;++i) siz[i]=siz[i>>1]+((i&1)?1:0);
85     for (R i=1;i<=q;++i)
86     {
87         int t=cal(i);
88         if((siz[i]^(n-1))&1) ans=(ans-t+mod)%mod;
89         else ans=(ans+t)%mod;
90     }
91     printf("%d",ans);
92     return 0;
93 }

黑暗前的幻想乡

　　「Tree」：https://www.lydsy.com/JudgeOnline/problem.php?id=2631

　　题意概述：有一棵 $n$ 个点的树，要求支持链加，链乘，链求和，断边&&连边（保证操作后仍为树），$n,q<=10^5$

　　“保证操作后仍为树”这句话，就差明着写出来“建议使用LCT”了。

　　LCT+luogu线段树2 即可。另：模数虽小，乘法时仍需转long long.

  1 # include <cstdio>
  2 # include <iostream>
  3 # include <cstring>
  4 # include <string>
  5 # define R register int
  6 # define ll unsigned int
  7  
  8 using namespace std;
  9  
 10 const int maxn=100005;
 11 const int mod=51061;
 12 int n,q,x,y,db;
 13 int ch[maxn][2],f[maxn],r[maxn],st[maxn];
 14 ll da[maxn],dm[maxn],s[maxn],siz[maxn],v[maxn];
 15 char opt[10];
 16  
 17 int read()
 18 {
 19     R x=0;
 20     char c=getchar();
 21     while (!isdigit(c)) c=getchar();
 22     while (isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar();
 23     return x;
 24 }
 25  
 26 bool isntroot (int x) { return ch[ f[x] ][0]==x||ch[ f[x] ][1]==x; }
 27  
 28 int D (int x) { return ch[ f[x] ][1]==x; }
 29  
 30 void update (int x)
 31 {
 32     int l=ch[x][0],r=ch[x][1];
 33     siz[x]=(siz[l]+siz[r]+1)%mod;
 34     s[x]=(s[l]+s[r]+v[x])%mod;
 35 }
 36  
 37 inline void turn (int x)
 38 {
 39     r[x]^=1;
 40     swap(ch[x][0],ch[x][1]);
 41 }
 42  
 43 inline void rev (int x)
 44 {
 45     r[x]=0;
 46     if(ch[x][0]) turn(ch[x][0]);
 47     if(ch[x][1]) turn(ch[x][1]);
 48 }
 49  
 50 inline void pushdown (int x)
 51 {
 52     if(dm[x]==1&&da[x]==0&&r[x]==0) return;
 53     if(r[x]) rev(x);
 54     int l=ch[x][0],r=ch[x][1];
 55     if(l)
 56     {
 57         v[l]=(v[l]*dm[x]+da[x])%mod;
 58         s[l]=(s[l]*dm[x]+siz[l]*da[x])%mod;
 59         dm[l]=dm[l]*dm[x]%mod;
 60         da[l]=(da[l]*dm[x]+da[x])%mod;
 61     }
 62     if(r)
 63     {
 64         v[r]=(v[r]*dm[x]+da[x])%mod;
 65         s[r]=(s[r]*dm[x]+siz[r]*da[x])%mod;
 66         dm[r]=dm[r]*dm[x]%mod;
 67         da[r]=(da[r]*dm[x]+da[x])%mod;
 68     }
 69     dm[x]=1; da[x]=0;
 70 }
 71  
 72 void rotate (int x)
 73 {
 74     if(db) printf("rotate(%d)\n",x);
 75     int F=f[x],g=f[F],d=D(x),df=D(F);
 76     pushdown(F); pushdown(x);
 77     int k=ch[x][d^1];
 78     ch[F][d]=k;
 79     ch[x][d^1]=F;
 80     if(isntroot(F)) ch[g][df]=x;
 81     if(k)f[k]=F; f[F]=x; f[x]=g;
 82     update(F); update(x);
 83 }
 84  
 85 void splay (int x)
 86 {
 87     if(db) printf("splay(%d)\n",x);
 88     int y=x,tp=0;
 89     st[++tp]=x;
 90     while(isntroot(y)) st[++tp]=f[y],y=f[y];
 91     while(tp) pushdown(st[tp]),tp--;
 92     while(isntroot(x))
 93     {
 94         int F=f[x],g=f[g];
 95         if(!isntroot(F)) rotate(x);
 96         else if(D(x)==D(F)) rotate(F),rotate(x);
 97         else rotate(x),rotate(x);
 98     }
 99 }
100  
101 void access (int x)
102 {
103     if(db) printf("access(%d)\n",x);
104     int y=0;
105     while(x)
106     {
107         splay(x);
108         ch[x][1]=y;
109         update(x);
110         y=x; x=f[x];
111     }
112 }
113  
114 void make_root (int x)
115 {
116     if(db) printf("make_root(%d)\n",x);
117     access(x);
118     splay(x);
119     turn(x);
120 }
121  
122 void spilt (int x,int y)
123 {
124     if(db) printf("spilt(%d,%d)\n",x,y);
125     make_root(x);
126     access(y);
127     splay(y);
128 }
129  
130 void link (int x,int y)
131 {
132     if(db) printf("link(%d,%d)\n",x,y);
133     make_root(x);
134     f[x]=y;
135 }
136  
137 void cut (int x,int y)
138 {
139     if(db) printf("cut(%d,%d)\n",x,y);
140     spilt(x,y);
141     f[x]=0; ch[y][0]=0;
142     update(y);
143 }
144  
145 void mul (int x,int y,int c)
146 {
147     c%=mod;
148     spilt(x,y);
149     v[y]=v[y]*c%mod; s[y]=s[y]*c%mod;
150     da[y]=da[y]*c%mod; dm[y]=dm[y]*c%mod;
151 }
152  
153 void add (int x,int y,int c)
154 {
155     c%=mod;
156     spilt(x,y);
157     v[y]=(v[y]+c)%mod; s[y]=(s[y]+siz[y]*c)%mod;
158     da[y]=(da[y]+c)%mod;
159 }
160  
161 int main()
162 {
163     scanf("%d%d",&n,&q);
164     for (R i=1;i<=n;++i)
165         v[i]=siz[i]=s[i]=dm[i]=1;
166     for (R i=1;i<n;++i)
167     {
168         x=read(),y=read();
169         link(x,y);
170     }
171     for (R i=1;i<=q;++i)
172     {
173         int c;
174         scanf("%s",opt);
175         if(opt[0]=='+')
176         {
177             x=read(),y=read(),c=read();
178             add(x,y,c);
179         }
180         else if(opt[0]=='-')
181         {
182             x=read(),y=read();
183             cut(x,y);
184             x=read(),y=read();
185             link(x,y);
186         }
187         else if(opt[0]=='*')
188         {
189             x=read(),y=read(),c=read();
190             mul(x,y,c);
191         }
192         else if(opt[0]=='/')
193         {
194             x=read(),y=read();
195             spilt(x,y);
196             printf("%u\n",s[y]);
197         }
198     }
199     return 0;
200 }

Tree

　　「BBQ Easy」：https://atcoder.jp/contests/agc001/tasks/agc001_a

　　题意概述：给定 $2n$ 个数，请你将它们两两配对，每组的权值即为两个数中的较小值，求权值和的最大值。$n<=100$

　　最小的数不管和谁配，权值都是它，那么没必要配很大的，配第二小的最好。以此类推，排序后相邻的两两配对，就是最优方案。

 1 # include <cstdio>
 2 # include <iostream>
 3 # include <algorithm>
 4 # define R register int
 5  
 6 using namespace std;
 7  
 8 const int maxn=205;
 9 int n,ans;
10 int l[maxn];
11  
12 int main()
13 {
14     scanf("%d",&n);
15     for (R i=1;i<=2*n;++i) scanf("%d",&l[i]);
16     sort(l+1,l+1+2*n);
17     for (R i=1;i<=n;++i)
18         ans+=l[2*i-1];
19     printf("%d",ans);
20     return 0;
21 }

BBQ Easy

　　「Mysterious Light」：https://atcoder.jp/contests/agc001/tasks/agc001_b

　　题意概述：请看原题面。

　　手工模拟几个，发现答案是 $(n-(n,k))\times 3$.我也不知道为什么

 1 # include <cstdio>
 2 # include <iostream>
 3 # define ll long long
 4  
 5 using namespace std;
 6  
 7 ll n,k;
 8  
 9 ll gcd (ll a,ll b) { return b?gcd(b,a%b):a; }
10  
11 int main()
12 {
13     scanf("%lld%lld",&n,&k);
14     printf("%lld",(n-gcd(n,k))*3);
15 }

Mysterious Light

4.18：

　　突发奇想打算做一点思维题，于是开始刷Atcoder。本来犹豫到底写哪个等级的题(NOIP前刷了一阵ABC)，想了想，觉得自己怎么说也可以算是一个省选选手(普及选手)了，所以决定做AGC。今天用了一上午加一下午写了一套ARC+一套AGC.AT的题目一般偏重思维，刚刚用百度搜了搜，发现几乎没有大数据结构，多项式，反演，网络流这类国内比较热门的考点，计算几何也挺少(不过中国现在也挺少考)，总的来说跟bzoj，codeforces风格迥异。所以不能光刷它，也得做点难写的题目。

　　「Reconciled?」：https://atcoder.jp/contests/arc076/tasks/arc076_a

　　题意概述：将 $n$ 只猴子和 $m$ 只狗排成一列，要求不能出现相邻的猴子或相邻的狗，求方案数。$n,m<=10^5$

　　首先假设 $n<=m$.如果 $n=m$ 那么可以这样插空：ABABAB，也可以这样：BABABA，所以方案数就是 $2\times n!\times m!$

　　如果$n+1=m$，那么只能这样：ABABABA，方案数为 $n!\times m!$

　　除此以外，不存在合法解。

 1 # include <cstdio>
 2 # include <iostream>
 3 # define R register int
 4  
 5 using namespace std;
 6  
 7 const int mod=1e9+7;
 8 int n,m;
 9  
10 int fac (int x)
11 {
12     int s=1;
13     for (R i=1;i<=x;++i) s=1LL*s*i%mod;
14     return s;
15 }
16  
17 int main()
18 {
19     scanf("%d%d",&n,&m);
20     if(n<m) swap(n,m);
21     if(n==m)
22         printf("%lld\n",2LL*fac(n)*fac(m)%mod);
23     else if(n==m+1)
24         printf("%lld\n",1LL*fac(n)*fac(m)%mod);
25     else puts("0");
26     return 0;    
27 }

Reconciled？

　　「Built?」：https://atcoder.jp/contests/arc076/tasks/arc076_b

　　题意概述：有 $n$ 个城市，每个城市有一个坐标，任意两城市间的距离为 $min(|x_1-x_2|,|y_1-y_2|)$ ,求最小生成树的代价。$n<=10^5$

　　做的时候想复杂了，先对xy分别排序，对于每一维，首先将每个点与下一个点的边push进堆，每取出一个后就将它能连出的下一条边也push进去。

　　其实完全可以更简单，那就是:只连相邻的边。因为“a->b->c”和“a->c”的花费是一样的，第一个不会比第二个劣。

 1 # include <cstdio>
 2 # include <iostream>
 3 # include <cstring>
 4 # include <algorithm>
 5 # include <string>
 6 # include <queue>
 7 # define R register int
 8 # define ll long long
 9 # define pac(a,b) make_pair(a,b)
10  
11 using namespace std;
12  
13 const int maxn=200005;
14 int n,m,h,d[maxn],vis[maxn],f[maxn];
15 int sx[maxn],sy[maxn],a,b;
16 ll ans=0;
17 struct node { int v,id; }X[maxn],Y[maxn];
18 typedef pair <int,int> pii;
19 priority_queue <pii,vector<pii>,greater<pii> > q1,q2;
20  
21 bool cmp (node a,node b) { return a.v<b.v; }
22  
23 int find (int x) { if(x!=f[x]) return f[x]=find(f[x]); return x; }
24  
25 int main()
26 {
27     scanf("%d",&n);
28     for (R i=1;i<=n;++i)
29     {
30         scanf("%d%d",&X[i].v,&Y[i].v);
31         X[i].id=i;
32         Y[i].id=i;
33     }
34     sort(X+1,X+1+n,cmp);
35     sort(Y+1,Y+1+n,cmp);
36     for (R i=1;i<n;++i)
37         q1.push(pac(X[i+1].v-X[i].v,i)),sx[i]=1;
38     for (R i=1;i<n;++i)
39         q2.push(pac(Y[i+1].v-Y[i].v,i)),sy[i]=1;
40     int s=0;
41     for (R i=1;i<=n;++i) f[i]=i;
42     while(s!=n-1)
43     {
44         int x=q1.top().first;
45         int y=q2.top().first;
46         if(x<y)
47         {
48             a=q1.top().second;
49             q1.pop();
50             b=a+sx[a];
51             x=X[a].id; y=X[b].id;
52             x=find(x),y=find(y);
53             if(x!=y) f[x]=y,s++,ans+=X[a+sx[a]].v-X[a].v;
54             if(a+sx[a]+1>n) continue;
55             sx[a]++;
56             q1.push(pac(X[a+sx[a]].v-X[a].v,a));
57         }
58         else
59         {
60             a=q2.top().second;
61             q2.pop();
62             b=a+sy[a];
63             x=Y[a].id; y=Y[b].id;
64             x=find(x),y=find(y);
65             if(x!=y) f[x]=y,s++,ans+=Y[a+sy[a]].v-Y[a].v;
66             if(a+sy[a]+1>n) continue;
67             sy[a]++;
68             q2.push(pac(Y[a+sy[a]].v-Y[a].v,a));
69         }
70     }
71     printf("%lld\n",ans);
72     return 0;
73 }

Built?

　　「Connected?」：https://atcoder.jp/contests/arc076/tasks/arc076_c

　　题意概述：一个平板上有一些数（数放在顶点上），每个数会出现两次，请用线把相应的两数连接，要求线不能相交，问是否可能。

　　乍一看以为线只能像管子一样直直地走，以为是个拆点+网络流，但是，当我看了样例...

　　这也太能绕了吧，还有这种操作？根据观察，可以发现，除非两个数都在边界上，否则无论如何也能连上，所以只需要考虑边界上的数。按照顺时针排列所有在边界上的数字，顺着进行扫描，如果某两对数出现交叉（用栈随便判断一下就可以），那么就无解。

 1 # include <cstdio>
 2 # include <iostream>
 3 # include <algorithm>
 4 # define R register int
 5  
 6 using namespace std;
 7  
 8 const int maxn=100005;
 9 int r,C,n,cnt,sta[maxn<<1],tp,a,b,c,d;
10 struct po { int x,y,d,id; }g[maxn<<1];
11  
12 bool cmp (po a,po b)
13 {
14     if(a.d!=b.d) return a.d<b.d;
15     if(a.d==1) return a.y<b.y;
16     else if(a.d==2) return a.x<b.x;
17     else if(a.d==3) return a.y>b.y;
18     return a.x>b.x;
19 }
20  
21 int main()
22 {
23     scanf("%d%d%d",&r,&C,&n);
24     for (R i=1;i<=n;++i)
25     {
26         scanf("%d%d%d%d",&a,&b,&c,&d);
27         if(a!=0&&a!=r&&b!=0&&b!=C) continue;
28         if(c!=0&&c!=r&&d!=0&&d!=C) continue;
29         ++cnt;
30         g[cnt].x=a; g[cnt].y=b; g[cnt].id=i;
31         ++cnt;
32         g[cnt].x=c; g[cnt].y=d; g[cnt].id=i;
33     }
34     for (R i=1;i<=cnt;++i)
35     {
36         if(g[i].x==0) g[i].d=1;
37         else if(g[i].y==C) g[i].d=2;
38         else if(g[i].x==r) g[i].d=3;
39         else if(g[i].y==0) g[i].d=4;
40     }
41     sort(g+1,g+1+cnt,cmp);
42     for (R i=1;i<=cnt;++i)
43     {
44         if(sta[tp]==g[i].id) { tp--; continue; }
45         sta[++tp]=g[i].id;
46     }
47     if(tp) puts("NO");
48     else puts("YES");
49     return 0;
50 }

Connected？

　　「Exhausted?」：https://atcoder.jp/contests/arc076/tasks/arc076_d

　　题意概述：$n$ 个人坐 $m$ 把椅子。每个人有一个要求，要求自己必须坐在 $1-l_i$ 或 $r_i-n$ 这段的某个椅子上。求最少需要加几把椅子(加的椅子可以放在实数位置)。$n,m<=10^5$

　　加椅子看起来挺神奇，其实很简单。只要一个人得不到椅子，就加一把，所以题目问的就是最多可以匹配多少人。

　　网络流是行不通的，因为点数边数都不少，即使使用线段树优化建图也不行。

　　考虑神奇的Hall定理。我们定义 $f(X)$ 为 $X$ 这个集合中人可以选的椅子集合的大小，答案就是最大的 $|X|-f(X)$.

　　人数不少，枚举人的集合是不可能的，但是可选的集合并不很多，因为一定是头尾两段区间的形式，所以枚举 $f$.

　　对于一个已知的可选集合，只需求出最大的满足这个的人集合。枚举右端点，希望求出对于所有左端点的“满足l<=s&&t<=r”的点的数量，就是一道很简单的扫描线题目了。

 1 # include <cstdio>
 2 # include <iostream>
 3 # include <algorithm>
 4 # define R register int
 5 # define nl (n<<1)
 6 # define nr (n<<1|1)
 7  
 8 using namespace std;
 9  
10 const int maxn=200005;
11 int n,m,delta[maxn<<2],t[maxn<<2],ans=0,qg;
12 struct peo { int l,r; }a[maxn];
13  
14 bool cmp (peo a,peo b) { if(a.l!=a.r) return a.l<b.l; return a.r<b.r; }
15  
16 void pushdown (int n)
17 {
18     int x=delta[n];
19     delta[nl]+=x;
20     delta[nr]+=x;
21     t[nl]+=x;
22     t[nr]+=x;
23     delta[n]=0;
24 }
25  
26 void add (int n,int l,int r,int ll,int rr,int v)
27 {
28     if(ll<=l&&r<=rr)
29     {
30         t[n]+=v; delta[n]+=v;
31         return;
32     }
33     int mid=(l+r)>>1;
34     if(delta[n]) pushdown(n);
35     if(ll<=mid) add(nl,l,mid,ll,rr,v);
36     if(rr>mid) add(nr,mid+1,r,ll,rr,v);
37     t[n]=max(t[nl],t[nr]);
38 }
39  
40 void build (int n,int l,int r)
41 {
42     if(l==r)
43     {
44         t[n]=r-m-1;
45         return;
46     }
47     int mid=(l+r)>>1;
48     build(nl,l,mid);
49     build(nr,mid+1,r);
50     t[n]=max(t[nl],t[nr]);
51 }
52  
53 int ask (int n,int l,int r,int ll,int rr)
54 {
55     if(ll<=l&&r<=rr)
56         return t[n];
57     int mid=(l+r)>>1,ans=-10000;
58     if(delta[n]) pushdown(n);
59     if(ll<=mid) ans=max(ans,ask(nl,l,mid,ll,rr));
60     if(rr>mid) ans=max(ans,ask(nr,mid+1,r,ll,rr));
61     return ans;
62 }
63  
64 int main()
65 {
66     scanf("%d%d",&n,&m);
67     for (R i=1;i<=n;++i)
68         scanf("%d%d",&a[i].l,&a[i].r);
69     sort(a+1,a+1+n,cmp);
70     build(1,0,m+1);
71     int p=1;
72     for (R i=0;i<=m;++i)
73     {
74         while(a[p].l<=i&&p<=n) add(1,0,m+1,1,a[p].r,1),p++;
75         ans=max(ans,ask(1,0,m+1,i+1,m+1)-i);
76     }
77     ans=max(ans,n-m);
78     printf("%d",ans);
79     return 0;
80 }