Usaco 2019 Jan Platinum
Usaco 2019 Jan Platinum
要不是昨天老师给我们考了这套题,我都不知道usaco还有铂金这么一级。
插播一则新闻:杨神坚持认为铂金比黄金简单,原因竟是:铜 汞 银 铂 金(金属活动性顺序表)
Usaco真是慢的不行,所以就贴洛谷链接啦。
Redistricting: https://www.luogu.org/problemnew/show/P5202
题意概述:给出一个长度为N的序列,由'H'和'G'组成,将它分为任意段,每段的长度不超过 K ,要求最小化(H比较少的段)的数量。k<=n<=3×105
首先可以将原序列中的G视为一,做一遍前缀和,那么就有了一个 O(NK) 的朴素dp:

# include <cstdio> # include <iostream> # include <cstring> # define nl (n<<1) # define nr (n<<1|1) # define R register int using namespace std; const int maxn=300005; const int inf=100000000; int n,k,a[maxn],f[maxn],g[maxn],q[maxn],H=1,T; char s[maxn]; void add (int x) { while(H<=T&&((f[x]<f[ q[T] ])||(f[x]==f[ q[T] ]&&g[x]<=g[ q[T] ]))) T--; q[++T]=x; } void del (int x) { while (H<=T&&q[H]<=x) H++; } int ask (int x) { if(g[ q[H] ]<g[x]) return f[ q[H] ]; return f[ q[H] ]+1; } int main() { scanf("%d%d",&n,&k); scanf("%s",s+1); for (R i=1;i<=n;++i) { if(s[i]=='G') a[i]=a[i-1]+1; else a[i]=a[i-1]; g[i]=i-2*a[i]; } f[0]=0; for (R i=1;i<=n;++i) { add(i-1); if(i-k-1>=0) del(i-k-1); f[i]=ask(i); } printf("%d",f[n]); return 0; }
exercise:https://www.luogu.org/problemnew/show/P5203
题意概述:首先给出一棵树,再给出一些连接树上两点的边,求有多少个环恰好经过两条非树边。n,m<=105
考试的时候打了暴力,结果只有样例分...网上关于这场比赛的中文题解好像很少,所以我就翻译一下官方题解好了(有的地方会省掉一些话,但是意思应该是不变的.): And,官方题解为什么每句话都要加个"我们"?
首先想一想哪些 "非树边" 对可以构成合法答案。我们定义一条非树边的 "路径" 为它连接的两点在树上的路径。如果两条非树边的 "路径" 有边相交(有一样的边),那么这就是一组合法的答案。
现在我们有了一个新的问题:如何判断有边相交的树上路径对数?首先我们认为这棵树是任意生根的(这句话只是为了翻出来好玩,其实意思就是无根树)。一条路径可能会有拐点,所以统计起来比较麻烦。那么将它拆成两条路径,一条是从A到LCA的,一条是从LCA到B的,再统计相交的路径会不会好做一点呢?如果用这种统计法,可能会有的路径对被重复计算,然而,重复计算的答案可以很容易地算出来。当且仅当两条路径的LCA相同,而且端点连接到LCA的方式相同(对应端点属于LCA的同一棵子树)时,这个答案才会被统计两次,所以我们可以先计算出这样路径对的数量,最后再从答案中减去即可。这样以来,我们就可以忽视重复计算的影响,转而解决一种非常简单的路径问题。
我们的问题现在被简化了。我们有一些从某个节点到它的某个祖先的路径,而且我们希望求出边相交的路径对数。考虑一个类似但更简单的问题:给出一些开区间(A,B),求有多少个区间相交?对于每个区间分别求出起点在它的范围内的区间数目,加起来就是答案(注意,如果两个区间具有相同的端点,答案可能会少一,所以要特殊处理),对于树上的路径,其实也没有什么差别,预处理一遍,做一个树上差分就可以了。当然,还是要注意有相同端点的那些路径。
题解程序的实现中有一些小trick,就是对于每条路径,认为它的起点是路径上深度次小的那个点,这样就巧妙的避免了,两条路径仅在端点处重合的问题。

1 # include <cstdio> 2 # include <iostream> 3 # include <map> 4 # define R register int 5 # define ll long long 6 7 using namespace std; 8 9 const int maxn=200005; 10 int firs[maxn],h=1,n,m,x[maxn],y[maxn],l[maxn],a,b,dep[maxn],f[maxn][20]; 11 struct edge { int too,nex; }g[maxn<<1]; 12 map <ll,int> M; 13 ll ans,d[maxn]; 14 15 int read() 16 { 17 R x=0; 18 char c=getchar(); 19 while (!isdigit(c)) c=getchar(); 20 while (isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar(); 21 return x; 22 } 23 24 void dfs (int x) 25 { 26 int j; 27 for (R i=firs[x];i;i=g[i].nex) 28 { 29 j=g[i].too; 30 if(dep[j]) continue; 31 f[j][0]=x; 32 for (R k=1;k<=18;++k) f[j][k]=f[ f[j][k-1] ][k-1]; 33 dep[j]=dep[x]+1; 34 dfs(j); 35 } 36 } 37 38 int lca (int x,int y) 39 { 40 if(dep[x]>dep[y]) swap(x,y); 41 for (R i=18;i>=0;--i) if(dep[y]-(1<<i)>=dep[x]) y=f[y][i]; 42 if(x==y) return x; 43 for (R i=18;i>=0;--i) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i]; 44 return f[x][0]; 45 } 46 47 int lcas (int x,int y) 48 { 49 if(x==y) return -1; 50 for (R i=18;i>=0;--i) if(dep[x]-(1<<i)>dep[y]) x=f[x][i]; 51 return x; 52 } 53 54 void pushdown (int x) 55 { 56 int j; 57 for (R i=firs[x];i;i=g[i].nex) 58 { 59 j=g[i].too; 60 if(dep[j]<dep[x]) continue; 61 d[j]+=d[x]; 62 pushdown(j); 63 } 64 } 65 66 void add (int x,int y) 67 { 68 g[++h].nex=firs[x]; 69 g[h].too=y; 70 firs[x]=h; 71 } 72 73 int main() 74 { 75 n=read(),m=read(); 76 m-=(n-1); 77 for (R i=1;i<n;++i) 78 { 79 a=read(),b=read(); 80 add(a,b),add(b,a); 81 } 82 dep[1]=1; 83 dfs(1); 84 for (R i=1;i<=m;++i) 85 { 86 x[i]=read(),y[i]=read(); 87 l[i]=lca(x[i],y[i]); 88 a=lcas(x[i],l[i]); 89 b=lcas(y[i],l[i]); 90 if(a>b) swap(a,b); 91 if(a!=-1) d[a]++,ans-=d[a]; 92 if(b!=-1) d[b]++,ans-=d[b]; 93 if(a!=-1&&b!=-1) 94 { 95 ans-=M[ a*n+b ]; 96 M[ a*n+b ]++; 97 } 98 } 99 pushdown(1); 100 for (R i=1;i<=m;++i) 101 ans+=d[ x[i] ]+d[ y[i] ]-2*d[ l[i] ]; 102 printf("%lld",ans); 103 return 0; 104 }
tracking2:https://www.luogu.org/problemnew/show/P5204
题意概述:给出对于长度为n的序列,窗口大小为k的滑动窗口最小值,求有多少原序列满足要求.额外要求:原序列中的数不能大于1e9.k<=n<=105
这题好毒瘤...考场写了一个假装 k<=10 的状压dp,只有样例分。那么下面是翻译的英文题解。(这次写题解的人稍微少用了一些“我们”):
首先,介绍一种记数法。给出一个序列 a1,a2,…an (小n,而不是整个序列的长度N), 也就是滑动窗口的最小值:
{min
当看到一个接近这样的问题时,想想它的简化版本往往是很有帮助的。我们现在来看这样一个问题:有多少序列的滑动窗口最小值是这样的?
\underbrace{v, v, \ldots, v}_{N - K + 1 \text{ times }}?
定义 MX = 10^9 , x=MX−v . 定义 dp[u] 为长度为 u 的序列满足滑动窗口最小值全是 v,而且以 v 结尾。下面通过枚举最右端的那个 v 来计算答案,我们就得到了如下方程:
DP[v] = DP[v-1] + xDP[v-2] + \ldots + x^{K - 1}DP[v - K]
在这里 x 表示严格大于 v 的数的数目.这样就有了一个复杂度为 O(NK) 的解法, 不过我们还可以做得更好,像这样:
DP[v+1] = DP[v] + x(DP[v] - x^{K - 1}DP[v - K])
这样就是 O(N) 了。定义 c(len,v) 为长度为 len ,滑动窗口最小值全为 v 且以 v 结尾的序列个数.
现在我们已经解决了这个简单的问题。再从整体上看一看原来的这个问题。假设滑动窗口中两个相邻的数不相同,而且不失一般性地假设左边比右边大,也就是说:
a = \min(a_i, a_{i + 1}, \ldots , a_{i + K - 1}) > \min(a_{i+1}, a_{i+2}, \ldots , a_{i + K}) = b
因为 a = \min(a_i, a_{i + 1}, \ldots , a_{i + K - 1}) \le \min(a_{i + 1}, a_{i + 2}, \ldots , a_{i + K - 1}) 所以说 a_{i+K}=b .
这就表明,如果两个滑动窗口的值是不同的,我们就可以直接知道某些值。这样就引出了一种新的表示法:将滑动窗口表示为一些数对 (值,连续出现次数),举个例子:
(5, 3, 3, 3, 3, 2) \mapsto ((5, 1), (3, 4), (2, 1)).
下一步可能最好还是结合一个例子来解释。假设 K=2, 滑动窗口的值为 (2,2,2,3,3,3,1,1) . 根据刚刚的推断,序列就可以被表示为这样的形式:(a,b,2,c,d,e,f,1,g) . 现在 c,d,e,f 的滑动窗口最小值就是(3,3,3), a,b 的滑动窗口最小值就是(2,2), g的滑动窗口最小值就是(1)。因此问题就可以转化为最早的那个形式,相当于求c(3,4)×c(2,2)×c(1,1).
还有两个小问题:一个是结尾,一个是...这句我真的翻译不出来了,直接粘过来:“;
最后是我自己的理解了:如果不合并,有的段就会被算多次,但是采用一些巧妙的方法,不压缩应该也是可以的。
我翻的很像机翻吗?其实我写的中文题解有时候看起来也像机翻。

1 # include <cstdio> 2 # include <cstring> 3 # include <iostream> 4 # define R register int 5 # define ll long long 6 using namespace std; 7 8 const int maxn=100005; 9 const ll mod=1000000007; 10 const int mx=1000000000; 11 int dp[maxn],a[maxn],n,k; 12 int sub (int a,int b) { a-=b; a=(a%mod+mod)%mod; return a; } 13 int mul (int a,int b) { a=1LL*a*b%mod; return a; } 14 15 int qui (int a,int b) 16 { 17 int s=1; 18 while(b) 19 { 20 if(b&1) s=mul(s,a)%mod; 21 a=mul(a,a)%mod; 22 b>>=1; 23 } 24 return s; 25 } 26 27 int c (int v,int len) 28 { 29 dp[0]=dp[1]=1; 30 int x=mx-v; 31 int p=qui(x,k); 32 for (R i=2;i<=len;++i) 33 { 34 dp[i]=mul(x+1,dp[i-1]); 35 if(i-k-1<0) continue; 36 dp[i]=sub(dp[i],mul(p,dp[i-k-1])); 37 } 38 return dp[len]; 39 } 40 41 int main() 42 { 43 scanf("%d%d",&n,&k); 44 for (R i=1;i<=n-k+1;++i) 45 scanf("%d",&a[i]); 46 int l=1,r,ans=1,len; 47 while(l<=n-k+1) 48 { 49 r=l; 50 while(a[r+1]==a[l]) r++; 51 len=r-l+k; 52 if(l!=1&&a[l-1]>a[l]) len-=k; 53 if(r!=n-k+1&&a[r+1]>a[r]) len-=k; 54 if(len>=0) ans=mul(ans,c(a[l],len+1)); 55 l=r+1; 56 } 57 printf("%d",ans); 58 return 0; 59 }
求解C那里,我给len加了一个一,这是为什么呢...因为刚刚的定义是:c(len,v) 为长度为 len ,滑动窗口最小值全为 v 且以 v 结尾的序列个数,但是实际应用中,最后一个数并不需要是 v,所以多算一位,再把最后一位截去即可。
终于全都补完了!这套题的实现难度不是很大,但是思路却很巧妙。
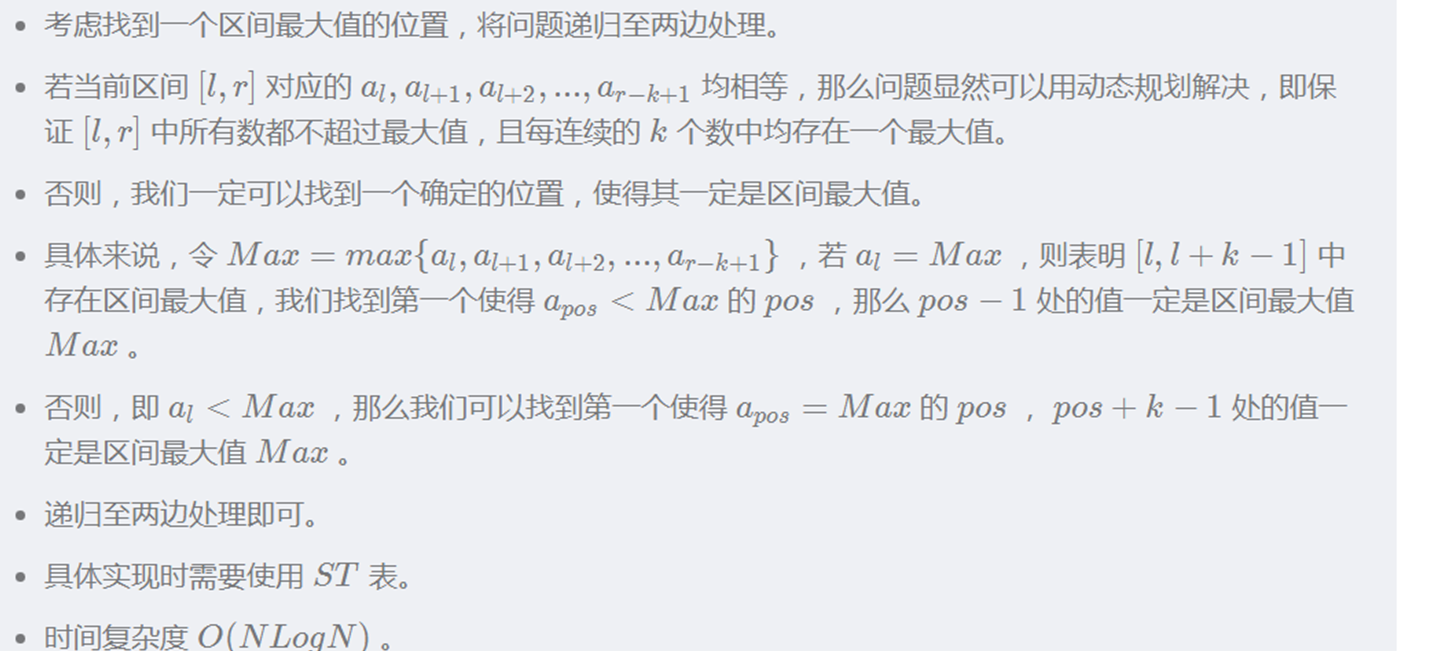
老师也发了一份题解,但是那个做法看起来比较难写,可能大概好懂一点?反正我没懂。一并放上来,如果有人能看懂也是件好事。相同段的处理是一样的,但是套一层rmq我就不懂是什么操作了。
那么下一场再见啦!虽然我大概率不打下一场
---shzr




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步