AC自动机
AC自动机
最近机房的同学们都在学字符串,$asuldb$已经做了一大批$manacher$的题目了,于是学习AC自动机.
AC自动机=Trie+kmp;
但是它也有其独特的地方,可以做一些很奇妙的题目.
开始正文部分:
前置知识:Trie树,kmp(咕咕咕了所以是别人的链接) .
建议先把这两个看懂,但是我个人觉得不会也没关系...
AC自动机是一种用处众多的多模式串匹配算法,可以代替kmp.由于本身就是Trie树的一种扩展,完全可以当做Trie来用.这三种字符串算法都非常优秀,在各自专长的领域都可以达到理论下界(输入复杂度).
kmp:单模式串单文本串;
trie:功能类似于AC自动机,但是只能处理前缀/后缀相关问题;
AC自动机:多模式串单文本串;
举例子是一种非常有用的学习方法,所以来举一个例子:
模式串:aba,bab
首先造一棵Trie出来,这肯定没有什么坏处.
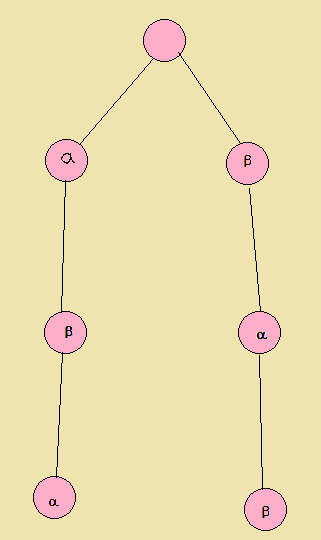
然后是建立fail指针,先上图再解释吧.

从yyb大佬的blog中抄了一句:fail指针是指:沿着其父节点的失配指针,一直向上,直到找到拥有当前这个字母作为子节点的节点,将fail指针指向它的那个子节点.
其实这句话可以说是非常清楚明白了...
但是难道我们要一直暴力的往上跳去找那个子节点吗?看起来复杂度会变的非常不科学,所以有一个奇妙的操作:如果自己缺少某个儿子,那么将fail指针指向的儿子继承过来!
因为这个操作是递归进行的,所以某个点的儿子表示的就是它这一整条fail链上的儿子集合,而且保留的是离自己最近的那个.如果不明白,那么仔细想一想,或者画个图.
这只是说了fail的定义,那么它的实际含义是什么呢?这里和kmp类似,我尝试描述一下:fail指针指向的是(使得(从头开始并以fail指针作为结束的字符串)与(以当前节点作为结束字符的字符串的后缀)相同)的节点中深度最深的那个.我知道上述的一些话非常绕口,所以用了括号表示从句的嵌套关系.
如果明白了上面的说法,那么fail的构建过程也就非常简单了,用一个bfs即可.
下面是匹配,还是一口气写完比较好,否则明天又忘了.
首先和Trie树匹配是一样的,从头开始匹配,但是如果出现匹配不上的情况,不用从头开始找,而是像kmp一样跳一跳,只不过这里的跳不是显式的转换到fail指针上去.别忘了刚刚对儿子进行了一个继承,所以假装什么都没有发生过一样愉快的走儿子即可,不过事实上此儿子已经并非你的儿子了...意会即可.
既然有了这么多神奇的新定义,自然就可以在这上面做一点文章了,似乎有的题是专把fail提出来树剖的?似乎有的题是考察fail性质的?不过首先定义是必须要掌握的.
一个虽然简单但是很容易被绕晕的地方:
为什么匹配的时候不会漏过某些字符串?看书的时候就是想不明白,后来发现并不难理解,首先将看起来很容易遗漏的情况分个类:
1.两个模式串本质上是相同的,那么建立Trie的时候就自然建到了一起,不用担心啦~
2.acd,cd为模式串,acd为文本串,看起来好像匹配完acd就漏掉了cd,但是第一个d的fail指向第二个d,所以也不会漏掉.
AC自动机(简单版):https://www.luogu.org/problemnew/show/P3808
题意概述:这道题是一道很模板的模板题.求有多少模式串在文本串中出现过.
每跳到一个节点就遍历它发出的整条fail链,统计结束标记的数量,因为不能重复统计,所以统计完改为-1.

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # include <queue> 5 # define R register int 6 7 using namespace std; 8 9 const int maxn=1000006; 10 int n,cnt=0; 11 char s[maxn]; 12 queue <int> q; 13 struct Trie 14 { 15 int ch[maxn][26]; 16 int vis[maxn]; 17 int fail[maxn]; 18 void clear() 19 { 20 memset(ch,0,sizeof(ch)); 21 memset(vis,0,sizeof(vis)); 22 } 23 void ins() 24 { 25 int x=0,c,len=strlen(s+1); 26 for (R i=1;i<=len;++i) 27 { 28 c=s[i]-'a'; 29 if(!ch[x][c]) ch[x][c]=++cnt; 30 x=ch[x][c]; 31 } 32 vis[x]++; 33 } 34 void build() 35 { 36 for (R i=0;i<26;++i) 37 { 38 if(ch[0][i]) 39 { 40 fail[ ch[0][i] ]=0; 41 q.push(ch[0][i]); 42 } 43 } 44 int beg; 45 while(q.size()) 46 { 47 beg=q.front(); 48 q.pop(); 49 for (R i=0;i<26;++i) 50 { 51 if(ch[beg][i]) 52 { 53 fail[ ch[beg][i] ]=ch[ fail[beg] ][i]; 54 q.push(ch[beg][i]); 55 } 56 else ch[beg][i]=ch[ fail[beg] ][i]; 57 } 58 } 59 } 60 int ac() 61 { 62 int len=strlen(s+1); 63 int n=0,x,j,ans=0; 64 for (R i=1;i<=len;++i) 65 { 66 x=s[i]-'a'; 67 n=ch[n][x]; 68 j=n; 69 while(j&&vis[j]!=-1) 70 { 71 ans+=vis[j]; 72 vis[j]=-1; 73 j=fail[j]; 74 } 75 } 76 return ans; 77 } 78 }t; 79 80 int main() 81 { 82 scanf("%d",&n); 83 for (R i=1;i<=n;++i) 84 { 85 scanf("%s",s+1); 86 t.ins(); 87 } 88 t.build(); 89 scanf("%s",s+1); 90 printf("%d",t.ac()); 91 return 0; 92 }
AC自动机(加强版):https://www.luogu.org/problemnew/show/P3796
题意概述:求出现次数最多的模式串数量.
记录每个模式串的结束位置,用文本串匹配时顺便打一些标记表示有多少次可以匹配到此处,匹配完后统计即可.网上的做法似乎很丰富,不过我感觉我这个就挺好...而且时间复杂度也非常科学.

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # include <queue> 5 # define R register int 6 7 using namespace std; 8 9 const int maxn=1000006; 10 const int maxz=20500; 11 int n,ed[200]; 12 char s[151][80],st[maxn]; 13 queue <int> q; 14 struct FSM 15 { 16 int ch[maxz][26],cnt; 17 int fail[maxz],vis[maxn]; 18 void clear() 19 { 20 cnt=0; 21 memset(ch,0,sizeof(ch)); 22 memset(fail,0,sizeof(fail)); 23 memset(vis,0,sizeof(vis)); 24 } 25 int ins (int d) 26 { 27 int x=0,c,len=strlen(s[d]+1); 28 for (R i=1;i<=len;++i) 29 { 30 c=s[d][i]-'a'; 31 if(!ch[x][c]) ch[x][c]=++cnt; 32 x=ch[x][c]; 33 } 34 return x; 35 } 36 void build() 37 { 38 int n; 39 for (R i=0;i<26;++i) 40 if(ch[0][i]) 41 q.push(ch[0][i]); 42 while(q.size()) 43 { 44 n=q.front(); 45 q.pop(); 46 for (R i=0;i<26;++i) 47 { 48 if(ch[n][i]) 49 { 50 fail[ ch[n][i] ]=ch[ fail[n] ][i]; 51 q.push(ch[n][i]); 52 } 53 else ch[n][i]=ch[ fail[n] ][i]; 54 } 55 } 56 } 57 void AC() 58 { 59 int t,c,n=0,len=strlen(st+1); 60 for (R i=1;i<=len;++i) 61 { 62 c=st[i]-'a'; 63 n=ch[n][c]; 64 t=n; 65 while(t) 66 { 67 vis[t]++; 68 t=fail[t]; 69 } 70 } 71 } 72 }t; 73 74 int main() 75 { 76 scanf("%d",&n); 77 while(n) 78 { 79 t.clear(); 80 for (R i=1;i<=n;++i) 81 { 82 scanf("%s",s[i]+1); 83 ed[i]=t.ins(i); 84 } 85 t.build(); 86 int m=0; 87 scanf("%s",st+1); 88 t.AC(); 89 for (R i=1;i<=n;++i) 90 m=max(m,t.vis[ ed[i] ]); 91 printf("%d\n",m); 92 for (R i=1;i<=n;++i) 93 if(t.vis[ ed[i] ]==m) 94 printf("%s\n",s[i]+1); 95 scanf("%d",&n); 96 } 97 return 0; 98 }
---shzr



