八大板块算法讲解(自用)
1.搜索
DFS(深度优先搜索)
DFS
对于每一个点,枚举其连着的边,再到此点重复操作,直到无法继续遍历。
if(当前点所连边数=0){
(按题目要求);
返回;
}
for(0~当前点所连边条数)
if(该边所连点不等于上各点) dfs(所连点,当前点);
IDDFS
与dfs不同的是,每次深搜都会有搜索的最大深度限制,如果没有找到解,那么就增大深度,再进行深搜,如此循环直到找到解为止,这样可以找到最浅层的解。
while(!dfs(cnt))
cnt++;
BFS(广度优先搜索)
BFS
从起始节点开始,依次遍历当前节点的所有邻居节点,然后再依次遍历邻居节点的所有邻居节点,直到遍历到目标节点或者遍历完所有节点。
将起点推入队列中;
将起点标识为已走过;
while(队列非空){
取队列首节点vt,并从队列中弹出;
探索上面取出得节点的周围是否有没走过的节点vf,如果有将所有能走的vf的parents指向vt,并将vf加入队列(如果vf等于终点,说明探索完成,退出循环);
}
双向BFS
同时从两个方向BFS,一旦搜索到相同的值,意味着找到了一条联通起点和终点的最短路径。
剪枝
顾名思义,就是通过一些判断,砍掉搜索树上不必要的子树。这些子树可能是不可达的,也可能是可达但显然不是最优的,去掉它们对最终答案没有影响,所以我们称为“剪枝”。
把常用的剪枝分成以下两类。 1.可行性剪枝。 2.最优性剪枝。
用队列记录当前所连的点,分层重复此操作,知道所有点被访问过为止。
字符串
字符串哈希
如果我们要比较一个字符串, 我们不直接比较字符串, 而是比较它们对应映射的数字, 这样子就知道两个"子串"是否相等. 从而达到子串的 \(Hash\) 值的时间为 \(O(1)\), 进而可以利用"空间换时间"来节省时间复杂度。
#define base 233
unsigned long long hash(char s[]){
long long ans=0,len=strlen(s);
for(long long i=0;i<len;i++)
ans=base*ans+(ull)s[i];
return ans;
}
KMP
主旨是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()数组实现,数组本身包含了模式串的局部匹配信息。
inline void get_nxt(){ //nxt数组是从S[0到i-1]前子串的前缀后缀最大值
int t1=0,t2;
nxt[0]=t2=-1;
while(t1<len2)
if(t2==-1||s2[t1]==s2[t2]) nxt[++t1]=++t2;
else t2=nxt[t2];
}
inline void KMP(){
int t1=0,t2=0;
while(t1<len1){
if(t2==-1 || s1[t1]==s2[t2])
t1++,t2++;
else t2=nxt[t2];
if(t2==len2) printf("%d\n",t1-len2+1),t2=nxt[t2];
}
}
字典树
先放一张图
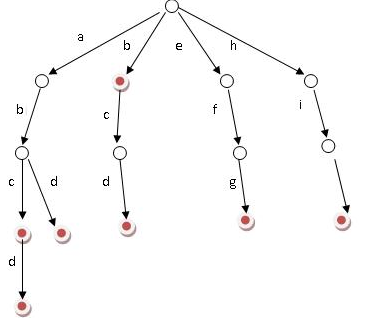
- 根节点没字符,其余每一个子节点都包含一个字符
- 从根节点到某一节点。路径上经过的字符连接起来,就是该节点对应的字符串
- 每个节点的所有子节点包含的字符都不相同
用于统计,排序和保存大量的字符串(不仅限于字符串),经常被搜索引擎系统用于文本词频统计。
数论
同余
给定一个正整数 \(m\),如果两个整数 \(a\) 和 \(b\) 满足 \(a-b\) 能够被 \(m\) 整除,即 \((a-b)\div m\) 得到一个整数,那么就称整数 \(a\) 与 \(b\) 对模 \(m\) 同余,记作 \(a≡b(mod\ m)\)。对模 \(m\) 同余是整数的一个等价关系。
定理
1.同余式相加:若 \(a≡b(mod\ m)\),\(c≡d(mod\ m)\),则 \(a+c≡b+d(mod\ m)\);
2.同余式相乘:若 \(a≡b(mod\ m)\),\(c≡d(mod\ m)\),则 \(a\times c≡b\times d(mod\ m)\)。
3.线性运算:如果 \(a≡b(mod\ m)\),\(c≡d(mod\ m)\),那么(1) \(a ± c ≡ b ± d (mod\ m)\);(2) \(a * c ≡ b * d (mod\ m)\)。
4.除法:若 \(a\div c≡b\div c(mod\ m)\ \ c≠0\) 则 \(a≡b(mod\ m\div gcd(c,m))\) 其中 \(gcd(c,m)\) 表示 \(c,m\) 的最大公约数。特殊地 , \(gcd(c,m)=1\) 则 \(a≡b(mod\ m)\)。
5.幂运算:如果 \(a≡b(mod\ m)\) 那么 \(a^n≡b^n(mod\ m)\)。
6.若 \(a≡b(mod\ m)\),\(n|m\) ,则 \(a≡b(mod\ n)\)
欧拉函数
定义:
对于一个正整数 \(n\),欧拉函数 \(φ(n)\) 表示小于等于 \(n\) 的正整数中与 \(n\) 互质的数的个数。
特殊的,当 \(n\) 为质数,\(φ(n)\ =\ n-1\)。
费马小定理
有两个整数 \(n,m\),如果其互质,那么 \(n\) 的 \(m-1\) 次幂对 \(m\) 取模与 \(1\) 恒等于。
如果要分数取模就要用乘法逆元,即 \(a\div b\) 对质数 \(p\) 取模就是 \(a\times b^{\ (p-2)\ }mod\ p\)。
动态规划
背包
01背包
定义:\(f[i][v]\) 表示前 \(i\) 件物品恰放入一个容量为 v 的背包可以获得的最大价值。
转移方程:f[i][v]=max(f[i-1][v],f[i-1][v-c[i]]+w[i])。
for(1~n,i)
for(V~0,v)
f[v]=max{f[v],f[v-c[i]]+w[i]};
完全背包
定义:\(f[i][v]\) 表示前 \(i\) 种物品恰放入一个容量为 \(v\) 的背包的最大权值。
转移方程:f[i][v]=max(f[i][v-c[i]]+w[i],f[i-1][v]);
for(1~n,i)
for(0~V,v)
f[v]=max{f[v],f[v-c[i]]+w[i]};
混合背包
即先判断是哪种背包,再进行对应操作
for(1~n,i)
if第i件物品是01背包
for(V~0,v)
f[v]=max{f[v],f[v-c[i]]+w[i]};
else if第i件物品是完全背包
for(0~V,v)
f[v]=max{f[v],f[v-c[i]]+w[i]};
线性dp
精髓
主打的就是个随机应变,码前先想好状态和转移方程,其他的轻而易举。
例题1 最大连续子序列和
题目:给定一个序列:\(S_1,S_2,S_3…S_n\),有 \(i,j\) 使得 \(sum=S_i+S_{i+1}…+S_{j-1}+S_j\) 最大,求最大值。
思路:首先先明确好状态:我们设数组 \(dp[n]\) 当中存放的是以当前的 \(i\),即 \(dp[i]\) 是以 \(S_i\) 为结尾的最大连续子列的和。
那么对于每个 \(dp[i]\) 会有两种情况:
- 将 \(S_i\) 放进:
dp[i]=dp[i-1]+S[i]; - 不将 \(s_i\) 放进:
dp[i]=S[i];
显然,对于每个 \(i(1\sim n)\) 的 \(dp[i]\) ,在两种情况中取大的,其次注意边界:dp[1]=S[1];
例题2 最长不下降子序列
题目:给定一个序列:\(S_1,S_2,S_3…S_n\),找到一个最长的子序列,可以是不连续的,使得其是不下降的序列(非递减的),求此序列的长度。
思路:\(dp[i]\) 表示的是当前点所在子序列的左端点编号,先展示一下核心代码:
for(int i=1;i<=n;i++){
dp[i]=1; //注意边界!
for(int j=1;j<i;j++)
if(S[i]>=S[j]&&dp[j]+1>dp[i]) dp[i]=dp[j]+1; //从第一个开始依次看是否有比自己小的,有才可以加进去
}
为什么这道题是两层循环不像上题呢?举个例子:
一个序列 \(S\ ={1, 1, 4, 1, 1, 4 }\)。按照上一题:对于每一个 \(i\),只考虑 \(i-1\) 的话,答案是 \(3\),但注意题目是 可以是不连续的,这样的话答案是 \(5\),为什么错了呢?因为我们枚举到 \(S_4\) 的时候我们发现 \(S_4<S_3\),于是 dp[4]=4;,但因为不连续,所以我们可以从 \(1\sim i-1\) 枚举,所以故得出答案。
还有很多经典例题,随机应变是脱离不了的,但状态与转移方程式是绝对少不了的!
区间dp
精髓
正所谓 区间 DP ,就是在区间上进行 \(DP\) 。区间 \(DP\) 以区间的长度划分阶段,记录两个端点的坐标,通过合并小区间的最优解来求出大区间的最优解。
例题1 石子合并
题目:\(n\) 堆石子摆成一个环,每次选相邻的 \(2\) 堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分。求:将 \(n\) 堆石子合并成 \(1\) 堆的最小得分和最大得分。
思路:先考虑最小的分:先假设石子的摆放并不是环形,而是一条直线。首先,会想到要将第 \(l\) 堆石子和第 \(r\) 堆石子合并就要先将第 \(l\sim r\) 堆石子全部合并:设 \(dp[l][r]\) 为合并第 \(l\sim r\) 堆石子的最小的得分,假设区间 \(l\sim r\) 最后一次合并的两区间是 \(l\sim k-1\) 和 \(k\sim r\) ,则有状态转移方程:dp[l][r]=dp[l][k-1]+dp[k][r];
树形DP
精髓
有些问题,我们从根节点出发,向子节点做深度优先搜索,对于树上的每个节点(除根节点外),由父节点的信息(父节点合并后的信息,除去该孩子的信息,就是其与孩子的信息)更新该节点的信息。
例题1 树上动态规划
题目:给出一个 \(n\) 个节点的树,找出一个节点为根,使得树上所有节点的深度之和最大。
思路:dfs一遍,由子节点信息得到整棵树以1为根节点时,以x为根的子树的节点数量(\(size[x]\))和整棵树以1为根节点时,以x为根的子树的所有节点的深度之和(\(f[x]\))。再dfs一遍,由父节点信息得到整棵树以x为根时所有节点的深度之和(\(ans[x]\)),求出最大值 \(O(n)\)
DP核心部分:
void dp(int u,int fa){
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa) continue;
ans[v]=ans[u]+n-2*size[v];
dp(v,u);
}
}
例题2 树上01背包问题
题目:给出一棵有 \(n\) 个点的有根树,根节点的编号为1,初始的时候,树上所有边都没有被通,而每通一条边都需要一定的能量。每个点都只有 \(m\) 点能量,并且只能用来打通其和儿子之间的边,求最多有多少个点和根节点联通。
思路:\(dp[i]\):表示以 \(i\) 为根节点的子树最多能有多少个和 \(i\) 联通,那么可以把 \(u\) 的每个子节点 \(v\) 都看成一个物品,花费是打通 \(u,v\) 这条边的花费,而价值就是dp[v],所以求解每个点的dp值就成了一个01背包问题。
核心部分:
void dfs(int u,int fa){
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa)continue;
dfs(v,u);
}
memset(f,0,sizeof(f));
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
int cost=e[i].cost;
int val=dp[v];
if(v==fa)continue;
for(int j=m;j>=cost;j--){
f[j]=max(f[j],f[j-cost]+val);
}
}
dp[u]=f[m]+1;
}
图论
连通性
tanjan求强连通分量
首先我们需要两个变量:
- \(dfn_u\):深度优先搜索遍历时结点 \(u\) 被搜索的次序。
- \(low_u\):在 \(u\) 的子树中能够回溯到的最早的已经在栈中的结点。设以 \(u\) 为根的子树为 \(\textit{Subtree}_u\)。\(\textit{low}_u\) 定义为以下结点的 \(\textit{dfn}\) 的最小值:\(\textit{Subtree}_u\) 中的结点;从 \(\textit{Subtree}_u\) 通过一条不在搜索树上的边能到达的结点。
一个结点的子树内的所有节点的 \(dfn\) 都大于该结点的 \(dfn\);从根开始的一条路径上的 \(dfn\) 严格递增,\(low\) 严格非降。
顺序按深度优先搜索算法依次搜索,每次搜索维护当前节点的 \(dfn\) 和 \(low\),然后让此节点入栈,如果栈里已有此数,像小时候的拖拉机游戏:
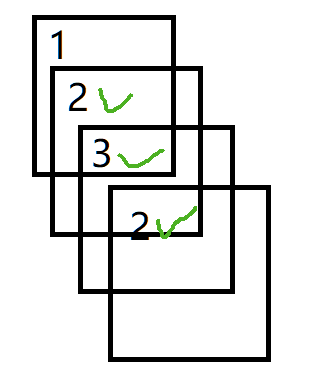
像这样,我们就把2,3牌收入囊中,即弹出栈。
最后当我们从节点 \(u->v\) 时,会有三种情况: - v到过,且在栈中,我们就用 \(dfn_v\) 去更新 \(low_u\)。
- v到过,不在栈中,这时说明已经处理过当前节点了,直接跳过。
- v没到过,继续对v作深度优先搜索,回溯时还要用 \(low_v\) 更新 \(low_u\),因为u能到v所以v能回溯到的节点u一定也行。
int dfn[MAXN], tot = 0;
bool instack[MAXN];
int low[MAXN];
std::stack<int> stk;
void dfs(int u){
dfn[u]=++tot;
low[u]=dfn[u]; // 一开始low[u]是自己,有后向边再更新
stk.push(u);
instack[u]=true;
for(int e=first[u];e;e=nxt[e]){
int v=go[e];
if(!dfn[v]){
dfs(v);
low[u]=min(low[u],low[v]); // 子节点更新了,我也要更新
// 若子节点没更新,则min能够保证low[u] == dfn[u]
}
else if(instack[v]) // v访问过且在栈中,意味着u→v是后向边
low[u]=min(low[u],dfn[v]); // 此处用min的原因是u→v可能是前向边,此时dfn[v]>dfn[u]
}
stk.pop();
instack[u]=false;
}
讲到这,顺带讲下tarjan染色
if(low[u]==dfn[u]) // 是SCC中的第一个被访问的节点
{
co[u]=++col;
while(stk.top()!=u) co[stk.top()]=col,instack[stk.top()]=false,stk.pop();
// 染色,弹栈
instack[u]=false;
stk.pop(); // 最后把u弹出去
}
求割点
定义:对于一个无向图,如果把一个点删除后这个图的极大连通分量数增加了,那么这个点就是这个图的割点。
先想到枚举每一个点,我们将他删掉后再判连通性,显然这样复杂度不优,我们又会想到我们刚刚所讲的tarjan中的 \(dfn\) 和 \(low\),我们依然dfs,如果当前节点 \(low_v \geq dfn_u\),即无法回到祖先,那么 \(u\) 为割点。
板子
求割边
定义:对于一个无向图,如果删掉一条边后图中的连通分量数增加了,则称这条边为桥或者割边。
和割点一样,只要改一处:\(low_v>dfn_u\) 就可以了。
板子
拓扑排序
暂无
欧拉图
定义:
- 欧拉回路:通过图中每条边恰好一次的回路
- 欧拉通路:通过图中每条边恰好一次的通路
- 欧拉图:具有欧拉回路的图
- 半欧拉图:具有欧拉通路但不具有欧拉回路的图
Hierholzer求欧拉回路:
从一条回路开始,每次任取一条目前回路中的点,将其替换为一条简单回路,以此寻找到一条欧拉回路。如果从路开始的话,就可以寻找到一条欧拉路。
最短路
floyd
直接贴了,没啥说的。。。
for (k = 1; k <= n; k++)
for (x = 1; x <= n; x++)
for (y = 1; y <= n; y++)
f[k][x][y] = min(f[k - 1][x][y], f[k - 1][x][k] + f[k - 1][k][y]);
dijkstra
每次操作选择点 \(u\) 可以到达的代价最小的点,一般用单调队列优化,依次弹出单调队列中的第一个,然后用一个dis[v]数组表示1到u的最小距离,然后我们用式子dis[v]=dis[u]+w[v];,其中w数组只权值,这样就有一个 \(O(nlogn)\) 的算法求最短路了。
板子
#include<bits/stdc++.h>
using namespace std;
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > q;
struct node{
int to,w,nxt;
}e[200005];
int dis[100005],head[100005],n,m,s,cnt;
void add(int u,int v,int d){
cnt++;
e[cnt].w=d;
e[cnt].to=v;
e[cnt].nxt=head[u];
head[u]=cnt;
}
void dij(){
memset(dis,0x3f3f3f3f,sizeof(dis));
dis[s]=0;
q.push({0,s});
while(!q.empty()){
int d=q.top().first,u=q.top().second;
q.pop();
if(d!=dis[u]) continue;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(dis[u]+e[i].w<dis[v]){
dis[v]=dis[u]+e[i].w;
q.push({dis[v],v});
}
}
}
}
int main(){
cin>>n>>m>>s;
for(int i=1;i<=m;i++){
int u,v,d;
cin>>u>>v>>d;
add(u,v,d);
}
dij();
for(int i=1;i<=n;i++)
cout<<dis[i]<<" ";
return 0;
}
但因为我们每次选的最小所以我们不能处理有负值的图。
SPFA
接上回:虽然dij有优秀的复杂度,但他不能处理有负值的图,这时我们就要用一个比较玄学的算法了:
关于SPFA:他死了
为什么会死?首先你要知道SPFA的过程:
- 建立一个队列,初始时队列里只有起始点,在建立一个表格记录起始点到所有点的最短路径(该表格的初始值要赋为极大值,该点到他本身的路径赋为0)
- 执行松弛操作,用队列里有的点去刷新起始点到所有点的最短路,如果刷新成功且被刷新点不在队列中则把该点加入到队列最后。
- 重复执行直到队列为空。
在稠密图中他会可能退化到 \(n^2\)!
生成树
我们定义无向连通图的最小生成树为边权和最小的生成树。
Prim算法:
贪心策略:每次选择到下一个点权最小的边,来个例子:
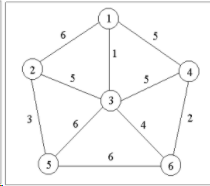
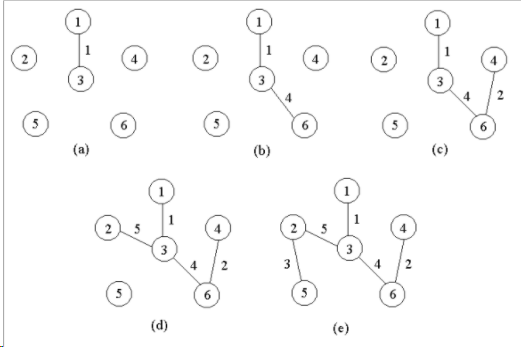
真正实现其实跟楼上dij很像,只是有一个地方存在差别,就是dis[]数组记录的含义是不一样的,dij算法中的是源点到其余顶点的最短距离,而这里的是顶点v到集合S之间的距离。
线性代数
单位矩阵
就像数字 \(1\times x=x\) 一样,设一个矩阵A和一个单位矩阵B,那么 \(A\times B=A\),一句话:一个矩阵乘以另一个矩阵仍是这个矩阵,那么另一个矩阵就是单位矩阵。
求法:暴力枚举每一个点,当当前横排号与竖排号相等时标号为1,否则为0。
矩阵乘法
首先我们要了解矩阵乘法的方法:设矩阵A乘以矩阵B得到矩阵C,就是A阵的第i行和B阵的第j列的元素两两相乘再相加,举个例子:
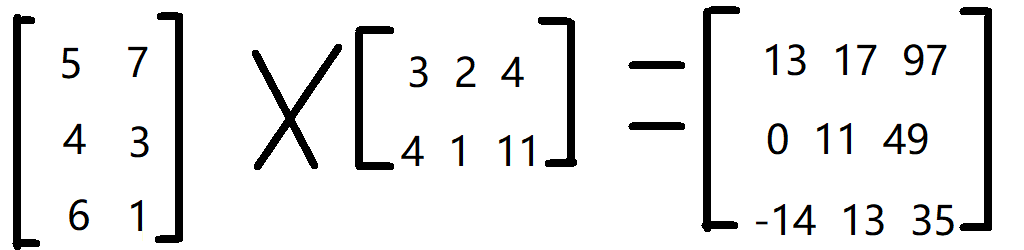
本例中,结果矩阵第2行第3列的元素值为49,它通过下列计算而得:4×4+3×11=49
求的话枚举即可。
快速幂
快速幂,顾名思义是快速计算指数的值的例如 \(2^{1000000000}\),如果一次一次 \(\times 2\) 的话显然会T,拿 \(2^{10}\) 举例子:
\(4=2^2\)
\(16=4^2=2^4\)
\(64=8^2=4^4=2^8\)
……
即\(2^n=4^{\tfrac{n}{2}}=8^{\tfrac{n}{4}}=……\)
这样复杂度是不是就低了很多?
那就贴板子了:
long long fpow(long long a,long long b){//a是底数,b是指数
long long ans=1;
while(b){//当指数不为0时执行
if(b%2==0){//指数为偶数时,指数除以2,底数乘以2
b/=2;
a*=a;
}else{//指数为奇数时,分离指数,ans乘以底数
ans*=a;
b--;
}
}
return ans;
}
这是精简:
long long fpow(long long a,long long b){
long long ans=1;
while(b){
if(b&1)ans*=a;
b>>=1;
a*=a;
}
return ans;
}
数据结构
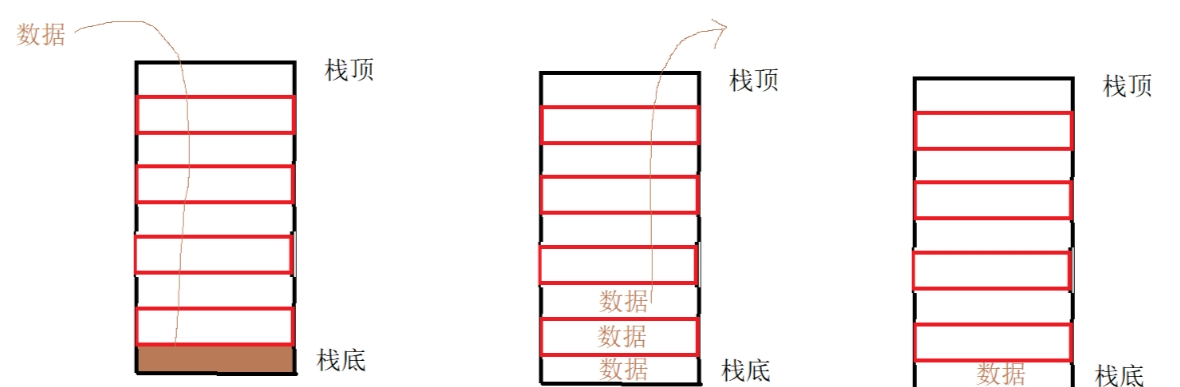
栈(stack)
栈是一种先进后出的数据结构,用一张图表示:
基本操作:
| 代码 | 含义 |
|---|---|
| stk.push() | 压栈,增加元素 |
| stk.pop() | 移除栈顶元素 |
| stk.top() | 取得栈顶元素(但不删除) |
| stk.empty() | 检测栈内是否为空,空为真 |
| stk.size() | 返回stack内元素的个数 |
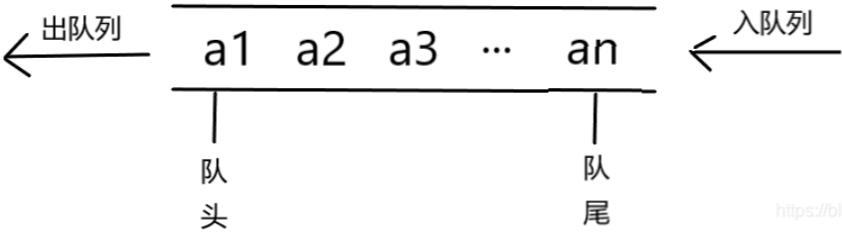
队列(queue)
队列
队列是一种先进先出的数据结构,用一张图表示:
基本操作:
| 代码 | 含义 |
|---|---|
| q.front() | 返回队首元素 |
| q.back() | 返回队尾元素 |
| q.push() | 尾部添加一个元素副本 进队 |
| q.pop() | 删除第一个元素 |
| q.size() | 返回队列中元素个数,返回值类型unsigned int |
| q.empty() | 判断是否为空,队列为空,返回true |
优先队列(priority_queue)
队列中的元素按照一定的优先级进行排序和访问。
priority_queue<int,vector<int>, greater<int> > pq; 降序。
priority_queue<int, vector<int>, less<int> >pq; 升序。
操作跟普通队列几乎一样。
ST表
前置芝士:倍增
顾名思义,倍增就是不停地翻倍。它能够使线性的处理转化为对数级的处理,大大地优化时间复杂度。
ST表就是运用了倍增思想的一个数据结构,主要解决区间最大值/最小值查询,\(O(nlogn)\) 预处理,\(O(1)\) 查询,但缺点是不能修改。
ST表使用的是一个二维数组 \(f[i][j]\) 来表示区间 \([i,\ i+2^j-1]\) 的答案,就拿求最大值举例子。
显然的 \(f[i][0]=a_i\),根据定义,我们有转移方程式 \(f[i][j]=max(f[i][j-1],f[2+i^{j-1}][j-1])\)。


