hdu 1198 Farm Irrigation

Problem Description

Benny has a spacious farm land to irrigate. The farm land is a rectangle, and is divided into a lot of samll squares. Water pipes are placed in these squares. Different square has a different type of pipe. There are 11 types of pipes, which is marked from A to K, as Figure 1 shows.


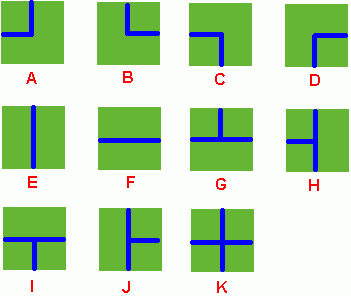
Figure 1

Benny has a map of his farm, which is an array of marks denoting the distribution of water pipes over the whole farm. For example, if he has a map 

ADC
FJK
IHE

then the water pipes are distributed like 


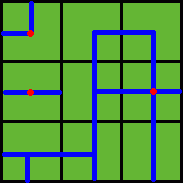
Figure 2

Several wellsprings are found in the center of some squares, so water can flow along the pipes from one square to another. If water flow crosses one square, the whole farm land in this square is irrigated and will have a good harvest in autumn. 

Now Benny wants to know at least how many wellsprings should be found to have the whole farm land irrigated. Can you help him? 

Note: In the above example, at least 3 wellsprings are needed, as those red points in Figure 2 show.

 

 

Input

There are several test cases! In each test case, the first line contains 2 integers M and N, then M lines follow. In each of these lines, there are N characters, in the range of 'A' to 'K', denoting the type of water pipe over the corresponding square. A negative M or N denotes the end of input, else you can assume 1 <= M, N <= 50.

 

 

Output

For each test case, output in one line the least number of wellsprings needed.

 

 

Sample Input

2 2 DK HF 3 3 ADC FJK IHE -1 -1

 

 

Sample Output

2 3

 

 

Author

ZHENG, Lu

 

 

Source

Zhejiang University Local Contest 2005

题目大意：看起来很复杂，但其实是一道比较简单的问题，就是有点烦，首先给了你A~K种水管的铺法，然后给你一个图，问要是所有的方块都通水至少需要多少水源。

分析：实际上就是求连通分支数，主要就是构图，我用了一个很2的方法建了个4维的数组来记录图。

#include <iostream>
#include <cstdio>
#include <cstring>
#define maxlen 60
using namespace std;
char maps[maxlen][maxlen];
bool visited[maxlen][maxlen];
bool g[maxlen][maxlen][maxlen][maxlen];
int n,m;
int di[][4]= {{1,0,0,1},{1,1,0,0},{0,0,1,1},{0,1,1,0},{1,0,1,0},{0,1,0,1},{1,1,0,1},{1,0,1,1},{0,1,1,1},{1,1,1,0},{1,1,1,1}};
int xx[]= {-1,0,1,0};
int yy[]= {0,1,0,-1};
bool judge(int x,int y)
{
    return x>=1&&x<=n&&y>=1&&y<=m;
}
int dfs(int i,int j)
{
    if(!judge(i,j)||visited[i][j])
        return 0;
    visited[i][j]=1;
    for(int k=0; k<4; ++k)
    {
        int nextx=i+xx[k];
        int nexty=j+yy[k];
        if(judge(nextx,nexty)&&!visited[nextx][nexty]&&g[i][j][nextx][nexty])
            dfs(nextx,nexty);
    }
    return 1;
}
int main ()
{
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        if(n<=0||m<=0)
            break;
        memset(g,0,sizeof(g));
        memset(maps,0,sizeof(maps));
        for(int i=1; i<=n; ++i)
        {
            for(int j=1; j<=m; ++j)
            {
                g[i][j][i][j]=1;
            }
        }
        for(int i=1; i<=n; ++i)
            for(int j=1; j<=m; ++j)
                cin>>maps[i][j];
        for(int i=1; i<=n; ++i)
        {
            for(int j=1; j<=m; ++j)
            {
                for(int k=0; k<4; ++k)
                {
                    if(di[maps[i][j]-'A'][k]&&judge(i+xx[k],j+yy[k])&&di[maps[i+xx[k]][j+yy[k]]-'A'][(k+2)%4])
                    {
                        g[i][j][i+xx[k]][j+yy[k]]=g[i+xx[k]][j+yy[k]][i][j]=1;
                    }
                }
            }
        }
        memset(visited,0,sizeof(visited));
        int ans=0;
        for(int i=1; i<=n; ++i)
        {
            for(int j=1; j<=m; ++j)
            {
                if(!visited[i][j])
                {
                    ans+=dfs(i,j);
                }
            }
        }
        printf("%d\n",ans);
    }
}