并查集专题

并查集是一种很方便实现也很有效的数据结构，应用也十分的广泛，主要包括两个操作，合并与查询，当然还有很多的变形。

一、先来很裸的并查集：uva 1160 - X-Plosives

X-Plosives

 

A secret service developed a new kind of explosive that attain its volatile property only when a specific association of products occurs. Each product is a mix of two different simple compounds, to which we call a binding pair. If N>2, then mixing N different binding pairs containing N simple compounds creates a powerful explosive. For example, the binding pairs A+B, B+C, A+C (three pairs, three compounds) result in an explosive, while A+B, B+C, A+D (three pairs, four compounds) does not.

 

You are not a secret agent but only a guy in a delivery agency with one dangerous problem: receive binding pairs in sequential order and place them in a cargo ship. However, you must avoid placing in the same room an explosive association. So, after placing a set of pairs, if you receive one pair that might produce an explosion with some of the pairs already in stock, you must refuse it, otherwise, you must accept it.

 

An example. Let’s assume you receive the following sequence: A+B, G+B, D+F, A+E, E+G, F+H. You would accept the first four pairs but then refuse E+G since it would be possible to make the following explosive with the previous pairs: A+B, G+B, A+E, E+G (4 pairs with 4 simple compounds). Finally, you would accept the last pair, F+H.

 

Compute the number of refusals given a sequence of binding pairs.

 

Input

The input will contain several test cases, each of them as described below. Consecutive test cases are separated by a single blank line.

 

 

Instead of letters we will use integers to represent compounds. The input contains several lines. Each line (except the last) consists of two integers (each integer lies between 0 and 105) separated by a single space, representing a binding pair. The input ends in a line with the number –1. You may assume that no repeated binding pairs appears in the input.

 

Output

For each test case, a single line with the number of refusals.

 

Sample Input

1 2

3 4

3 5

3 1

2 3

4 1

2 6

6 5

-1

 

Sample Output

3

题目大意：就是一队化合物如果是在同一个集合中的时候不能放入，问最后有多少队没有放入。

分析：很裸的并查集，只要在输入一队时判断一下是不是属于同一个集合，是的话计数器+1，否则合并。

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstring>
 4 #define maxlen 100010
 5 using namespace std;
 6 int father[maxlen];
 7 int n;
 8 int Find(int x)
 9 {
10     return father[x]==x?x:father[x]=Find(father[x]);
11 }
12 int main ()
13 {
14     int x,y;
15     while(scanf("%d",&x)!=EOF)
16     {
17         for(int i=0;i<=maxlen;++i)
18             father[i]=i;
19         int ans=0;
20         while(x!=-1)
21         {
22             scanf("%d",&y);
23             x=Find(x);
24             y=Find(y);
25             if(x==y)
26                 ++ans;
27             else
28                 father[x]=y;
29             scanf("%d",&x);
30         }
31         printf("%d\n",ans);
32     }
33 }
View Code

hdu 1232 畅通工程

Problem Description
某省调查城镇交通状况，得到现有城镇道路统计表，表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要互相间接通过道路可达即可）。问最少还需要建设多少条道路？ 
 

 

Input
测试输入包含若干测试用例。每个测试用例的第1行给出两个正整数，分别是城镇数目N ( < 1000 )和道路数目M；随后的M行对应M条道路，每行给出一对正整数，分别是该条道路直接连通的两个城镇的编号。为简单起见，城镇从1到N编号。 
注意:两个城市之间可以有多条道路相通,也就是说
3 3
1 2
1 2
2 1
这种输入也是合法的
当N为0时，输入结束，该用例不被处理。 
 

 

Output
对每个测试用例，在1行里输出最少还需要建设的道路数目。 
 

 

Sample Input
4 2 1 3 4 3 3 3 1 2 1 3 2 3 5 2 1 2 3 5 999 0 0
 

 

Sample Output
1 0 2 998
Hint
Hint
Huge input, scanf is recommended.
 

 

Source
浙大计算机研究生复试上机考试-2005年
 

 题目大意：n个城市通路，m条边，问最后还需要多少条路要修。

分析：裸的并查集。

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <cmath>
 5 #define maxlen 1100
 6 int father[maxlen];
 7 int n,m;
 8 void init()
 9 {
10     for(int i=0;i<=n;++i)
11         father[i]=i;
12 }
13 int Find(int x)
14 {
15     return father[x]==x?x:father[x]=Find(father[x]);
16 }
17 void Union(int x,int y)
18 {
19     x=Find(x),y=Find(y);
20     if(x==y)
21         return ;
22     father[x]=y;
23 }
24 int main ()
25 {
26     int x,y;
27     while(scanf("%d",&n),n)
28     {
29         scanf("%d",&m);
30         init();
31         while(m--)
32         {
33             scanf("%d%d",&x,&y);
34             Union(x,y);
35         }
36         int ans=0;
37         for(int i=1;i<=n;++i)
38         {
39             if(father[i]==i)
40                 ans++;
41         }
42         printf("%d\n",ans-1);
43     }
44 }
View Code

hdu 1213 How Many Tables

Problem Description
Today is Ignatius' birthday. He invites a lot of friends. Now it's dinner time. Ignatius wants to know how many tables he needs at least. You have to notice that not all the friends know each other, and all the friends do not want to stay with strangers.

One important rule for this problem is that if I tell you A knows B, and B knows C, that means A, B, C know each other, so they can stay in one table.

For example: If I tell you A knows B, B knows C, and D knows E, so A, B, C can stay in one table, and D, E have to stay in the other one. So Ignatius needs 2 tables at least.
 
Input
The input starts with an integer T(1<=T<=25) which indicate the number of test cases. Then T test cases follow. Each test case starts with two integers N and M(1<=N,M<=1000). N indicates the number of friends, the friends are marked from 1 to N. Then M lines follow. Each line consists of two integers A and B(A!=B), that means friend A and friend B know each other. There will be a blank line between two cases.
 
Output
For each test case, just output how many tables Ignatius needs at least. Do NOT print any blanks.
 
Sample Input
2
5 3
1 2
2 3
4 5
5 1
2 5
 
Sample Output
2
4
 
Author
Ignatius.L
 
Source
杭电ACM省赛集训队选拔赛之热身赛
分析：很裸的并查集，问有多少个集合。
 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <cmath>
 5 #define maxlen 10010
 6 using namespace std;
 7 int father[maxlen];
 8 int sum[maxlen];
 9 int n,m;
10 void init()
11 {
12     for(int i=0; i<=n; ++i)
13         father[i]=i;
14 }
15 int Find(int x)
16 {
17     return father[x]==x?x:father[x]=Find(father[x]);
18 }
19 void Union(int x,int y)
20 {
21     x=Find(x),y=Find(y);
22     if(x==y)
23         return;
24     father[x]=y;
25 }
26 int main ()
27 {
28     int t,x,y;
29     scanf("%d",&t);
30     while(t--)
31     {
32         scanf("%d%d",&n,&m);
33         init();
34         while(m--)
35         {
36             scanf("%d%d",&x,&y);
37             Union(x,y);
38         }
39         int ans=0;
40         for(int i=1; i<=n; ++i)
41         {
42             if(i==father[i])
43                 ans++;
44         }
45         printf("%d\n",ans);
46     }
47 }
View Code
hdu 1272 小希的迷宫

Problem Description

上次Gardon的迷宫城堡小希玩了很久（见Problem B），现在她也想设计一个迷宫让Gardon来走。但是她设计迷宫的思路不一样，首先她认为所有的通道都应该是双向连通的，就是说如果有一个通道连通了房间A和B，那么既可以通过它从房间A走到房间B，也可以通过它从房间B走到房间A，为了提高难度，小希希望任意两个房间有且仅有一条路径可以相通（除非走了回头路）。小希现在把她的设计图给你，让你帮忙判断她的设计图是否符合她的设计思路。比如下面的例子，前两个是符合条件的，但是最后一个却有两种方法从5到达8。 

Input

输入包含多组数据，每组数据是一个以0 0结尾的整数对列表，表示了一条通道连接的两个房间的编号。房间的编号至少为1，且不超过100000。每两组数据之间有一个空行。 
整个文件以两个-1结尾。

Output

对于输入的每一组数据，输出仅包括一行。如果该迷宫符合小希的思路，那么输出"Yes"，否则输出"No"。

Sample Input

6 8  5 3  5 2  6 4
5 6  0 0

8 1  7 3  6 2  8 9  7 5
7 4  7 8  7 6  0 0

3 8  6 8  6 4
5 3  5 6  5 2  0 0

-1 -1

Sample Output

Yes
Yes
No

Author

Gardon

Source

HDU 2006-4 Programming Contest

题目大意：判断是不是无环的图

分析：

1、判断成环的时候，只要判断输入边的两个点。有一个共同的父节点，那么这两个点就成环。

2、判断连通的时候，只要判断根节点数为1即可。

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <cmath>
 5 #define maxlen 100010
 6 int father[maxlen];
 7 int visited[maxlen];
 8 int n,m;
 9 int flag;
10 void init()
11 {
12     for(int i=0;i<=maxlen;++i)
13     {
14         father[i]=i;
15         visited[i]=0;
16     }
17 }
18 int Find(int x)
19 {
20     return father[x]==x?x:father[x]=Find(father[x]);
21 }
22 void Union(int x,int y)
23 {
24     x=Find(x),y=Find(y);
25     if(x==y)//成环
26     {
27         flag=0;
28         return ;
29     }
30     father[x]=y;
31 }
32 int main ()
33 {
34     int x,y;
35     while(scanf("%d%d",&x,&y)!=EOF)
36     {
37         if(x==-1&&y==-1)
38             break;
39         if(x==0&&y==0)
40         {
41             printf("Yes\n");
42             continue;
43         }
44         init();
45         Union(x,y);
46         visited[x]=visited[y]=1;
47         flag=1;
48         while(scanf("%d%d",&x,&y)!=EOF)
49         {
50             if(x==0&&y==0)
51                 break;
52             Union(x,y);
53             visited[x]=visited[y]=1;
54         }
55         int cnt=0;
56         for(int i=1;i<=maxlen;++i)
57         {
58             if(visited[i]&&father[i]==i)
59                 cnt++;
60             if(cnt>1)
61             {
62                 flag=0;
63                 break;
64             }
65         }
66         if(flag)
67             printf("Yes\n");
68         else
69             printf("No\n");
70     }
71 }
View Code

hdu 1325Is It A Tree?

Problem Description
A tree is a well-known data structure that is either empty (null, void, nothing) or is a set of one or more nodes connected by directed edges between nodes satisfying the following properties. 
There is exactly one node, called the root, to which no directed edges point. 

Every node except the root has exactly one edge pointing to it. 

There is a unique sequence of directed edges from the root to each node. 

For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not.



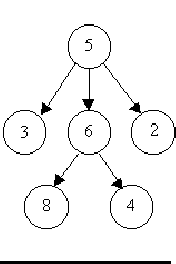
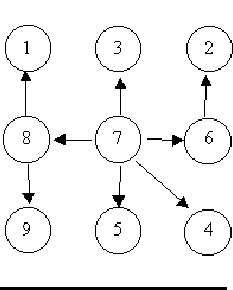
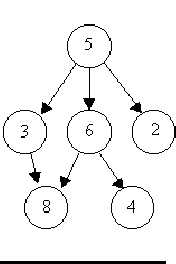
In this problem you will be given several descriptions of collections of nodes connected by directed edges. For each of these you are to determine if the collection satisfies the definition of a tree or not. 

 

 

Input
The input will consist of a sequence of descriptions (test cases) followed by a pair of negative integers. Each test case will consist of a sequence of edge descriptions followed by a pair of zeroes Each edge description will consist of a pair of integers; the first integer identifies the node from which the edge begins, and the second integer identifies the node to which the edge is directed. Node numbers will always be greater than zero. 
 
Output
For each test case display the line ``Case k is a tree." or the line ``Case k is not a tree.", where k corresponds to the test case number (they are sequentially numbered starting with 1). 
 
Sample Input
6 8 5 3 5 2 6 4
5 6 0 0
8 1 7 3 6 2 8 9 7 5
7 4 7 8 7 6 0 0
3 8 6 8 6 4
5 3 5 6 5 2 0 0
-1 -1
 
Sample Output
Case 1 is a tree.
Case 2 is a tree.
Case 3 is not a tree.
 
Source
North Central North America 1997
题目大意：判断是不是树。
分析：这个题目跟上面小希的迷宫很像，不过这是一个有向图上面那个是无向图。
1、无环
2、只有一个入度为0的结点，不存在入度大于1的结点。
3、注意空树也是树。比如输入0 0。
利用并查集来判环跟上面一样，增加一个indegree[i]数组记录入度，如果存在入度大于1的结点就不是树了。
 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstring>
 4 #define maxlen 100010
 5 int father[maxlen];
 6 int indegree[maxlen];
 7 int visited[maxlen];
 8 void init()
 9 {
10     for(int i=0; i<=maxlen; ++i)
11     {
12         father[i]=i;
13         indegree[i]=0;
14         visited[i]=0;
15     }
16 }
17 int Find(int x)
18 {
19     return father[x]==x?x:father[x]=Find(father[x]);
20 }
21 void Union(int x,int y)
22 {
23     x=Find(x),y=Find(y);
24     if(x==y)
25         return ;
26     father[y]=x;
27 }
28 int main ()
29 {
30     int x,y;
31     int flag=1;
32     int Case=1;
33     init();
34     while(scanf("%d%d",&x,&y)!=EOF)
35     {
36         if(x<0&&y<0)
37             break;
38         if(x==0&&y==0)
39         {
40             int ans=0;
41             for(int i=1; i<=maxlen; ++i)
42             {
43                 if(visited[i]&&Find(i)==i)
44                     ans++;
45                 if(indegree[i]>1)
46                 {
47                     flag=0;
48                     break;
49                 }
50             }
51             if(ans>1)
52                 flag=0;
53             if(flag)
54                 printf("Case %d is a tree.\n",Case++);
55             else
56                 printf("Case %d is not a tree.\n",Case++);
57             flag=1;
58             init();
59             continue;
60         }
61         else
62         {
63             visited[x]=visited[y]=1;
64             indegree[y]++;
65             Union(x,y);
66         }
67     }
68 }
View Code

hdu 1811 Rank of Tetris

Problem Description
自从Lele开发了Rating系统，他的Tetris事业更是如虎添翼，不久他遍把这个游戏推向了全球。

为了更好的符合那些爱好者的喜好，Lele又想了一个新点子：他将制作一个全球Tetris高手排行榜，定时更新，名堂要比福布斯富豪榜还响。关于如何排名，这个不用说都知道是根据Rating从高到低来排，如果两个人具有相同的Rating，那就按这几个人的RP从高到低来排。

终于，Lele要开始行动了，对N个人进行排名。为了方便起见，每个人都已经被编号，分别从0到N-1,并且编号越大，RP就越高。
同时Lele从狗仔队里取得一些（M个）关于Rating的信息。这些信息可能有三种情况，分别是"A > B","A = B","A < B"，分别表示A的Rating高于B,等于B,小于B。

现在Lele并不是让你来帮他制作这个高手榜，他只是想知道，根据这些信息是否能够确定出这个高手榜，是的话就输出"OK"。否则就请你判断出错的原因，到底是因为信息不完全（输出"UNCERTAIN"），还是因为这些信息中包含冲突（输出"CONFLICT"）。
注意，如果信息中同时包含冲突且信息不完全，就输出"CONFLICT"。
 
Input
本题目包含多组测试，请处理到文件结束。
每组测试第一行包含两个整数N,M(0<=N<=10000,0<=M<=20000),分别表示要排名的人数以及得到的关系数。
接下来有M行，分别表示这些关系
 
Output
对于每组测试，在一行里按题目要求输出
 
Sample Input
3 3
0 > 1
1 < 2
0 > 2
4 4
1 = 2
1 > 3
2 > 0
0 > 1
3 3
1 > 0
1 > 2
2 < 1
 
Sample Output
OK CONFLICT UNCERTAIN
 
Author
linle
 
Source
HDOJ 2007 Summer Exercise（2）

分析：根据题目意思，需要根据给的信息分析是不是有矛盾，有优先序列的关系我们很容易想到使用拓扑排序，但是等于号怎么解决？使用的就是并查集，把=两边的两个结点合并为一个集合，相同集合的点用一个点代替，然后在这些点里面进行拓扑排序判断。

注意：输出矛盾的优先级比不确定的高，先输出。

  1 #include <iostream>
  2 #include <cstdio>
  3 #include <cstring>
  4 #include <vector>
  5 #include <queue>
  6 #define maxlen 10010
  7 using namespace std;
  8 int father[maxlen];
  9 int indegree[maxlen];
 10 vector <int >v[maxlen];
 11 int a[maxlen*2],b[maxlen*2];
 12 char cmd[maxlen*2];
 13 int n,m;
 14 void init()
 15 {
 16     for(int i=0; i<=maxlen; ++i)
 17     {
 18         father[i]=i;
 19         indegree[i]=0;
 20         v[i].clear();
 21     }
 22 }
 23 int Find(int x)
 24 {
 25     return father[x]==x?x:father[x]=Find(father[x]);
 26 }
 27 bool Union(int x,int y)
 28 {
 29     x=Find(x),y=Find(y);
 30     if(x==y)
 31         return false;
 32     father[y]=x;
 33     return true;
 34 }
 35 void topo(int num)//拓扑排序
 36 {
 37     queue<int >q;
 38     for(int i=0;i<n;++i)//入度为零的点入队
 39     {
 40         if(i==Find(i)&&indegree[i]==0)
 41             q.push(i);
 42     }
 43     bool flag=true;
 44     while(!q.empty())
 45     {
 46         if(q.size()>1)
 47             flag=false;
 48         int x=q.front();
 49         q.pop();
 50         num--;
 51         for(int i=0;i<v[x].size();++i)
 52         {
 53             indegree[v[x][i]]--;
 54             if(indegree[v[x][i]]==0)
 55                 q.push(v[x][i]);
 56         }
 57     }
 58     if(num>0)
 59         printf("CONFLICT\n");
 60     else if(flag)
 61         printf("OK\n");
 62     else
 63         printf("UNCERTAIN\n");
 64 }
 65 int main ()
 66 {
 67     while(scanf("%d%d",&n,&m)!=EOF)
 68     {
 69         init();
 70         int num=n;
 71         for(int i=0;i<m;++i)
 72         {
 73             scanf("%d %c %d",&a[i],&cmd[i],&b[i]);
 74             if(cmd[i]=='=')
 75             {
 76                 if(Union(a[i],b[i]))
 77                     num--;
 78             }
 79         }
 80         for(int i=0;i<m;++i)
 81         {
 82             if(cmd[i]!='=')
 83             {
 84                 int x=Find(a[i]);
 85                 int y=Find(b[i]);
 86                 if(cmd[i]=='>')
 87                 {
 88                     v[x].push_back(y);//建边
 89                     indegree[y]++;
 90                 }
 91                 else
 92                 {
 93                     v[y].push_back(x);//建边
 94                     indegree[x]++;
 95                 }
 96             }
 97         }
 98         topo(num);
 99     }
100 }
View Code

二、加一点点难度，加权并查集：

hdu 1858More is better

Problem Description
Mr Wang wants some boys to help him with a project. Because the project is rather complex, the more boys come, the better it will be. Of course there are certain requirements.

Mr Wang selected a room big enough to hold the boys. The boy who are not been chosen has to leave the room immediately. There are 10000000 boys in the room numbered from 1 to 10000000 at the very beginning. After Mr Wang's selection any two of them who are still in this room should be friends (direct or indirect), or there is only one boy left. Given all the direct friend-pairs, you should decide the best way.
 
Input
The first line of the input contains an integer n (0 ≤ n ≤ 100 000) - the number of direct friend-pairs. The following n lines each contains a pair of numbers A and B separated by a single space that suggests A and B are direct friends. (A ≠ B, 1 ≤ A, B ≤ 10000000)
 
Output
The output in one line contains exactly one integer equals to the maximum number of boys Mr Wang may keep. 
 
Sample Input
4
1 2
3 4
5 6
1 6
4
1 2
3 4
5 6
7 8
 

 

Sample Output
4 2
Hint
A and B are friends(direct or indirect), B and C are friends(direct or indirect), then A and C are also friends(indirect). In the first sample {1,2,5,6} is the result. In the second sample {1,2},{3,4},{5,6},{7,8} are four kinds of answers.
 
Author
lxlcrystal@TJU
 
Source
HDU 2007 Programming Contest - Final

分析：最水的带权并查集了，问的是集合里面结点个数最多是多少。开一个sum数组记录每个集合的结点个数，合并的时候，把下面的个数加入到父节点上去，最后求一下最大值就可以了。

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <cmath>
 5 #define maxlen 100010
 6 using namespace std;
 7 int father[maxlen];
 8 int sum[maxlen];
 9 void init()
10 {
11     for(int i=0;i<=maxlen;++i)
12     {
13         father[i]=i;
14         sum[i]=1;
15     }
16 }
17 int Find(int x)
18 {
19     return father[x]==x?x:father[x]=Find(father[x]);
20 }
21 void Union(int x,int y)
22 {
23     x=Find(x),y=Find(y);
24     if(x==y)
25         return;
26     father[y]=x;
27     sum[x]+=sum[y];//更新sum
28 }
29 int main ()
30 {
31     int x,y;
32     int n;
33     int maxnum=0;
34     while(scanf("%d",&n)!=EOF)
35     {
36         init();
37         for(int i=0;i<n;++i)
38         {
39             scanf("%d%d",&x,&y);
40             Union(x,y);
41             int temp=max(x,y);
42             maxnum=max(temp,maxnum);
43         }
44         int ans=0;
45         for(int i=1;i<=maxnum;++i)
46             ans=max(ans,sum[i]);
47         printf("%d\n",ans);
48     }
49 }
View Code

uva 1329 - Corporative Network

A very big corporation is developing its corporative network. In the beginning each of the N enterprises of the corporation, numerated from 1 to N, organized its own computing and telecommunication center. Soon, for amelioration of the services, the corporation started to collect some enterprises in clusters, each of them served by a single computing and telecommunication center as follow. The corporation chose one of the existing centers I (serving the cluster A) and one of the enterprises J in some cluster B (not necessarily the center) and link them with telecommunication line. The length of the line between the enterprises I and J is |I - J|(mod 1000). In such a way the two old clusters are joined in a new cluster, served by the center of the old cluster B. Unfortunately after each join the sum of the lengths of the lines linking an enterprise to its serving center could be changed and the end users would like to know what is the new length. Write a program to keep trace of the changes in the organization of the network that is able in each moment to answer the questions of the users.

 

Input 

Your program has to be ready to solve more than one test case. The first line of the input file will contains only the number T of the test cases. Each test will start with the number N of enterprises (5≤N≤20000). Then some number of lines (no more than 200000) will follow with one of the commands:

E I  asking the length of the path from the enterprise I to its serving center in the moment;
I I J  informing that the serving center I is linked to the enterprise J.

The test case finishes with a line containing the word O. The I commands are less than N.

 

Output 

The output should contain as many lines as the number of E commands in all test cases with a single number each E the asked sum of length of lines connecting the corresponding enterprise with its serving center.

 

Sample Input 

1
4
E 3
I 3 1
E 3
I 1 2
E 3
I 2 4
E 3
O

Sample Output 

0
2
3
5
题目大意：定义了两个操作，E x表示询问x到根节点的距离，I x y表示把x的父亲结点设为y，两者之间的距离为|x-y|%1000。
分析：这里需要记录的是结点到根节点的距离，开一个数组dist[i]保存i结点到根的距离，初始时每个结点的根都是自己的，距离为0，在查询的时候，维护d[i]，更新这个值即可，在路径压缩的过程中更改i的父节点并更新距离即可。
 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <cmath>
 5 #define maxlen 20010
 6 using namespace std;
 7 int father[maxlen];
 8 int dist[maxlen];
 9 int n;
10 char cmd[10];
11 int myabs(int x)
12 {
13     return x>0?x:-x;
14 }
15 void init()
16 {
17     for(int i=0;i<=n;++i)
18     {
19         father[i]=i;
20         dist[i]=0;
21     }
22 }
23 int Find(int x)
24 {
25     if(father[x]==x)
26         return x;
27     else
28     {
29         int root=Find(father[x]);
30         dist[x]+=dist[father[x]];//更新dist
31         return father[x]=root;
32     }
33 }
34 int main ()
35 {
36     int t;
37     scanf("%d",&t);
38     while(t--)
39     {
40         scanf("%d",&n);
41         init();
42         int x,y;
43         while(scanf("%s",cmd)!=EOF)
44         {
45             if(cmd[0]=='O')
46                 break;
47             if(cmd[0]=='E')
48             {
49                 scanf("%d",&x);
50                 Find(x);
51                 printf("%d\n",dist[x]);
52             }
53             else if(cmd[0]=='I')
54             {
55                 scanf("%d%d",&x,&y);
56                 father[x]=y;//合并
57                 dist[x]=myabs(x-y)%1000;//计算距离
58             }
59         }
60     }
61 }
View Code

hdu 3926 Hand in Hand

Hand in Hand

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 122768/62768 K (Java/Others)
Total Submission(s): 975    Accepted Submission(s): 357

Problem Description

In order to get rid of Conan, Kaitou KID disguises himself as a teacher in the kindergarten. He knows kids love games and works out a new game called "hand in hand". 

Initially kids run on the playground randomly. When Kid says "stop", kids catch others' hands immediately. One hand can catch any other hand randomly. It's weird to have more than two hands get together so one hand grabs at most one other hand. After kids stop moving they form a graph.

Everybody takes a look at the graph and repeat the above steps again to form another graph. Now Kid has a question for his kids: "Are the two graph isomorphism?" 
 

Input

The first line contains a single positive integer T( T <= 100 ), indicating the number of datasets.
There are two graphs in each case, for each graph:
first line contains N( 1 <= N <= 10^4 ) and M indicating the number of kids and connections.
the next M lines each have two integers u and v indicating kid u and v are "hand in hand".
You can assume each kid only has two hands.
 
Output
For each test case: output the case number as shown and "YES" if the two graph are isomorphism or "NO" otherwise.
 
Sample Input
2
 
3 2
1 2
2 3
3 2
3 2
2 1
 
 
3 3
1 2
2 3
3 1
3 1
1 2
 
Sample Output
Case #1: YES
Case #2: NO
 
Source
2011 Multi-University Training Contest 9 - Host by BJTU
 
Recommend
xubiao
题目大意：判断两个图是不是同构。这个图只有链或者环。
分析：那么我们只需要用并查集把相连的结点都合并起来，如果发现有环，就进行标识。然后把两个图的并查集按照每颗树的节点个数大小排序，如果个数相同，那么有环的都放在前面。 然后，只要一一比较两个已排序的数组，只要发现有一个是不同的，就不是同构图。
  1 #include <iostream>
  2 #include <cstdio>
  3 #include <cstring>
  4 #include <cmath>
  5 #include <algorithm>
  6 #define maxlen 10010
  7 using namespace std;
  8 int father[maxlen];
  9 int sum[maxlen];
 10 int ring[maxlen];//标记成环点
 11 int n1,m1,n2,m2,numa,numb;
 12 struct node
 13 {
 14     int num;
 15     int isring;
 16     friend bool operator <(const node &a,const node &b)
 17     {
 18         return a.num==b.num?a.isring<b.isring:a.num<b.num;
 19     }
 20 } a[maxlen],b[maxlen];
 21 void init(int n)
 22 {
 23     memset(ring,0,sizeof(ring));
 24     for(int i=0; i<=n; ++i)
 25     {
 26         father[i]=i;
 27         sum[i]=1;
 28     }
 29 }
 30 int Find(int x)
 31 {
 32     return father[x]==x?x:father[x]=Find(father[x]);
 33 }
 34 void Union(int x,int y)
 35 {
 36     x=Find(x),y=Find(y);
 37     if(x==y)
 38     {
 39         ring[x]=1;//有环标记
 40         return;
 41     }
 42     sum[x]+=sum[y];//更新sum
 43     father[y]=x;
 44 }
 45 bool judge()//判断是否同构
 46 {
 47     if(numa!=numb)
 48         return false;
 49     sort(a,a+numa);
 50     sort(b,b+numb);
 51     for(int i=0; i<numa; ++i)
 52     {
 53         if(a[i].num!=b[i].num)
 54             return false;
 55         if (a[i].isring!=b[i].isring)
 56             return false;
 57     }
 58     return true;
 59 }
 60 int main ()
 61 {
 62     int t;
 63     int x,y;
 64     scanf("%d",&t);
 65     for(int Case=1; Case<=t; ++Case)
 66     {
 67         scanf("%d%d",&n1,&m1);
 68         init(n1);
 69         for(int i=0; i<m1; ++i)
 70         {
 71             scanf("%d%d",&x,&y);
 72             Union(x,y);
 73         }
 74         numa=0;
 75         for(int i=1; i<=n1; ++i)
 76         {
 77             if(i==Find(i))
 78             {
 79                 a[numa].num=sum[i];
 80                 a[numa].isring=ring[i];
 81                 numa++;
 82             }
 83         }
 84         scanf("%d%d",&n2,&m2);
 85         init(n2);
 86         for(int i=0; i<m2; ++i)
 87         {
 88             scanf("%d%d",&x,&y);
 89             Union(x,y);
 90         }
 91         if(n1!=n2||m1!=m2)
 92         {
 93             printf("Case #%d: NO\n",Case);
 94             continue;
 95         }
 96         numb=0;
 97         for(int i=1; i<=n2; ++i)
 98         {
 99             if(i==Find(i))
100             {
101                 b[numb].num=sum[i];
102                 b[numb].isring=ring[i];
103                 numb++;
104             }
105         }
106         if(judge())
107             printf("Case #%d: YES\n",Case);
108         else
109             printf("Case #%d: NO\n",Case);
110     }
111 }
View Code

hdu 2473 Junk-Mail Filter

Problem Description
 
Recognizing junk mails is a tough task. The method used here consists of two steps:
1) Extract the common characteristics from the incoming email.
2) Use a filter matching the set of common characteristics extracted to determine whether the email is a spam.

We want to extract the set of common characteristics from the N sample junk emails available at the moment, and thus having a handy data-analyzing tool would be helpful. The tool should support the following kinds of operations:

a) “M X Y”, meaning that we think that the characteristics of spam X and Y are the same. Note that the relationship defined here is transitive, so
relationships (other than the one between X and Y) need to be created if they are not present at the moment.

b) “S X”, meaning that we think spam X had been misidentified. Your tool should remove all relationships that spam X has when this command is received; after that, spam X will become an isolated node in the relationship graph.

Initially no relationships exist between any pair of the junk emails, so the number of distinct characteristics at that time is N.
Please help us keep track of any necessary information to solve our problem.
 
Input
There are multiple test cases in the input file.
Each test case starts with two integers, N and M (1 ≤ N ≤ 105 , 1 ≤ M ≤ 106), the number of email samples and the number of operations. M lines follow, each line is one of the two formats described above.
Two successive test cases are separated by a blank line. A case with N = 0 and M = 0 indicates the end of the input file, and should not be processed by your program.
 
Output
For each test case, please print a single integer, the number of distinct common characteristics, to the console. Follow the format as indicated in the sample below.
 
Sample Input
5 6
M 0 1
M 1 2
M 1 3
S 1
M 1 2
S 3
3 1
M 1 2
0 0
 
Sample Output
Case #1: 3
Case #2: 2
 
Source
2008 Asia Regional Hangzhou

题目大意：有N 封邮件, 编号 0 -> N-1，定义两种操作：

1、M x y: 合并操作, 将 2 种邮件合并为一种。

2、S x 分离操作, 将一封邮件独立出去, 单独占一个集合。

最后题目要求统计集合的个数。

分析：很容易想到是并查集，但这个删除怎么处理？查找资料知道如何操作，第一次碰到，学习了。

所谓的删除并不是真的删除，而是替换，当x 这个结点被删除时，只是将其的父亲换掉，单独形成一个集合，这个节点在树里的位置还是存在的，并不打乱树的结构。

具体的做法就是把0-n-1各结点初始化时都未叶子，有一个虚拟的父节点。那么后面的合并以及查找（路径压缩）都是在叶子上面操作了，不会影响整个树的结构。

注意：这种做法需要的空间复杂度很高，很容易爆栈，数组的大小需要注意，不要太大。错了好多次。

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <algorithm>
 5 using namespace std;
 6 int father[1350005];
 7 int id[125000];
 8 int inline Find(int x)
 9 {
10     return father[x]==x?x:father[x]=Find(father[x]);
11 }
12 void inline Union(int x,int y)
13 {
14     x=Find(x),y=Find(y);
15     if(x!=y)
16         father[x]=y;
17 }
18 int main ()
19 {
20     int n,m;
21     char cmd[10];
22     int x,y;
23     int Case=1;
24     while(scanf("%d%d",&n,&m)!=EOF)
25     {
26         if(n==0&&m==0)
27             break;
28         for(int i=0; i<n; ++i)
29             father[i]=i+n;
30         for(int i=n; i<=2*n+m; ++i)
31             father[i]=i;
32         int all=n+n;
33         for(int i=0; i<m; ++i)
34         {
35             scanf("%s",cmd);
36             if(cmd[0]=='M')
37             {
38                 scanf("%d%d",&x,&y);
39                 Union(x,y);
40             }
41             else if(cmd[0]=='S')
42             {
43                 scanf("%d",&x);
44                 father[x]=all++;
45             }
46         }
47         for(int i=0; i<n; ++i)
48             id[i]=Find(i);
49         sort(id,id+n);
50         int ans=1;
51         for(int i=1; i<n; ++i)
52         {
53             if(id[i]!=id[i-1])
54                 ans++;
55         }
56         printf("Case #%d: %d\n",Case++,ans);
57     }
58 }
View Code

稍后再更

posted @ 2013-08-11 10:37  默默如潮  阅读(438)  评论(0)  编辑  收藏  举报