小球自由落体动态模拟(Position Based Simulation)
在过去的几十年中,基于物理的三维物体动态模拟成为了计算机图形学的研究热点,其中最常见的方法是基于力(force-based)的模拟方法,比如弹簧质点模型(http://www.cnblogs.com/shushen/p/5473264.html),它把物体抽象成一系列质点以及连接这些质点的弹簧,然后通过离散化牛顿运动定律来模拟物体的运动情况。最近,基于位置的模拟方法在刚体、弹性体以及流体模拟方面都取得了不错的效果,基于位置(position-based)的模拟方法虽然没有基于力的模拟方法计算准确,但是它计算快速稳定,使其适用于实时交互应用领域。下面将详细介绍基于位置模拟算法的主要原理。

基于位置的模拟方法将研究物体抽象成N个粒子和M个限制条件的集合,整个算法流程如上图所示。首先初始化每个粒子的位置xi0和速度vi0(第1-3行),然后对于时间步长Δt而言,通过欧拉积分方法得到粒子下一时刻新的位置(第5-6行),新的位置pi并不是下一时刻的最终位置,而是下一时刻的预测位置,接着生成限制条件(第7行),并通过迭代方法不断修正预测位置pi使其满足限制条件(第8-10行),最后利用修正后的预测位置更新下一时刻的最终位置xi和速度vi(第11-14行)。
假设限制条件:C(x) = 0,一阶泰勒展开得到: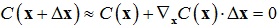 ,于是位置修正量为:
,于是位置修正量为: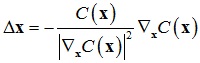 。
。
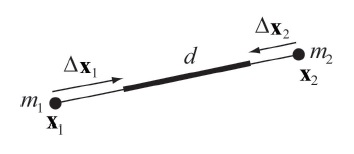
一种最简单的限制条件是距离限制,以两个粒子为例,其距离限制函数为:
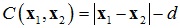
那么距离限制函数对各自的位置导数分别为:
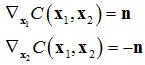
其中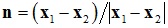 。
。
于是可以得到粒子的位置修正量为:
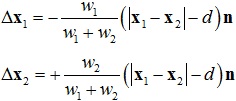

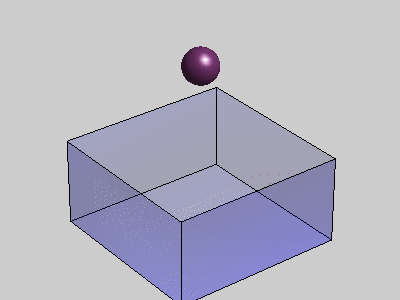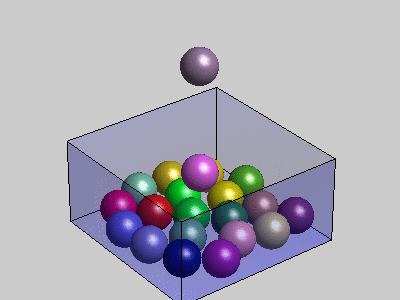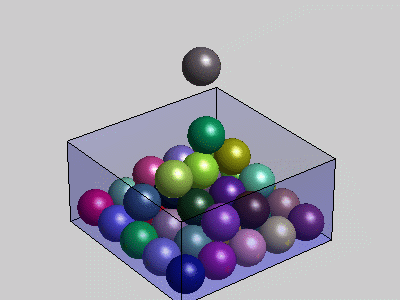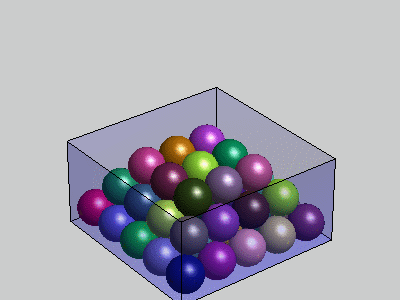
本文为原创,转载请注明出处:http://www.cnblogs.com/shushen。
参考文献:
[1] Bender, Jan, et al. "A Survey on Position-Based Simulation Methods in Computer Graphics." Computer Graphics Forum 33.6 (2014): 228-251.




 浙公网安备 33010602011771号
浙公网安备 33010602011771号