三维网格精简算法(Quadric Error Metrics)附源码
在计算机图形应用中,为了尽可能真实呈现虚拟物体,往往需要高精度的三维模型。然而,模型的复杂性直接关系到它的计算成本,因此高精度的模型在几何运算时并不是必须的,取而代之的是一个相对简化的三维模型,那么如何自动计算生成这些三维简化模型就是网格精简算法所关注的目标。
[Garland et al. 1997]提出了一种基于二次误差作为度量代价的边收缩算法,其计算速度快并且简化质量较高。该方法在选择一条合适的边进行迭代收缩时,定义了一个描述边收缩代价的变量Δ,具体如下:对于网格中的每个顶点v,我们预先定义一个4×4的对称误差矩阵Q,那么顶点v = [vx vy vz 1]T的误差为其二次项形式Δ(v) = vTQv。假设对于一条收缩边(v1, v2),其收缩后顶点变为vbar,我们定义顶点vbar的误差矩阵Qbar为Qbar = Q1 + Q2,对于如何计算顶点vbar的位置有两种策略:一种简单的策略就是在v1, v2和(v1+ v2)/2中选择一个使得收缩代价Δ(vbar)最小的位置。另一种策略就是数值计算顶点vbar位置使得Δ(vbar)最小,由于Δ的表达式是一个二次项形式,因此令一阶导数为0,即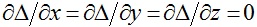 ,该式等价于求解:
,该式等价于求解:
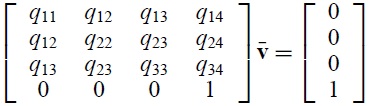
其中qij为矩阵Qbar中对应的元素。如果系数矩阵可逆,那么通过求解上述方程就可以得到新顶点vbar的位置,如果系数矩阵不可逆,就通过第一种简单策略来得到新顶点vbar的位置。根据以上描述,算法流程如下:

那么剩下的问题就是如何计算每个顶点的初始误差矩阵Q,在原始网格模型中,每个顶点可以认为是其周围三角片所在平面的交集,也就是这些平面的交点就是顶点位置,我们定义顶点的误差为顶点到这些平面的距离平方和:
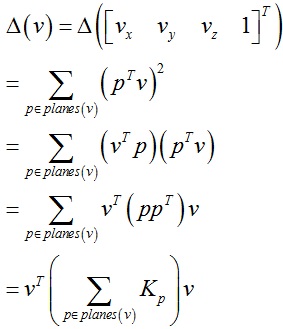
其中p = [a b c d]T代表平面方程ax + by + cz + d = 0(a2 + b2 + c2 = 1)的系数,Kp为二次基本误差矩阵:

因此原始网格中顶点v的初始误差为Δ(v) = 0,当边收缩后,新顶点误差为Δ(vbar) = vbarTQbarvbar,我们依次选取收缩后新顶点误差最小的边进行迭代收缩直到满足要求为止。

%% surface simplification using quadratic error metrics clc clear all close all load('bunny.mat'); V = surfdata.point; F = surfdata.face; nv = size(V,1); % total vertex number np = 0.1*nv; % remained vertex number % fundamental error quadric N = normals(V,F); N = normalizeVector3d(N); p = [N, -sum(N .* V(F(:,1),:), 2)]; Q0 = bsxfun(@times, permute(p, [2,3,1]), permute(p, [3,2,1])); % compute the Q matrices for all the initial vertices. nf = size(F,1); Q = zeros(4,4,nv); valence = zeros(nv,1); for i = 1:nf for j = 1:3 valence(F(i,j)) = valence(F(i,j)) + 1; Q(:,:,F(i,j)) = Q(:,:,F(i,j)) + Q0(:,:,i); end end % all valid pairs E = edges(F); % compute Q1+Q2 for each pair Qbar = Q(:,:,E(:,1)) + Q(:,:,E(:,2)); % a simple scheme: select either v1, v2 or (v1+v2)/2 ne = size(E,1); v1 = permute([V(E(:,1),:),ones(ne,1)], [2,3,1]); v2 = permute([V(E(:,2),:),ones(ne,1)], [2,3,1]); vm = 0.5 .* (v1 + v2); v = [v1, v2, vm]; cost = zeros(ne,3); cost(:,1) = sum(squeeze(sum(bsxfun(@times,v1,Qbar),1)).*squeeze(v1),1)'; cost(:,2) = sum(squeeze(sum(bsxfun(@times,v2,Qbar),1)).*squeeze(v2),1)'; cost(:,3) = sum(squeeze(sum(bsxfun(@times,vm,Qbar),1)).*squeeze(vm),1)'; figure; draw_t = 0; num = nv; tic for i = 1:nv-np if (nv - i) < 0.9*num num = nv - i; clf drawMesh(V, F, 'facecolor','y', 'edgecolor','k', 'linewidth', 1.2); view([0 90]) axis equal axis off camlight lighting gouraud cameramenu drawnow end [min_cost, vidx] = min(cost,[],2); [useless, k] = min(min_cost); e = E(k,:); % update position for v1 V(e(1),:) = v(1:3, vidx(k), k)'; V(e(2),:) = nan; % update Q for v1 Q(:,:,e(1)) = Q(:,:,e(1)) + Q(:,:,e(2)); Q(:,:,e(2)) = nan; % updata face F(F == e(2)) = e(1); f_remove = sum(diff(sort(F,2),[],2) == 0, 2) > 0; F(f_remove,:) = []; % collapse and delete edge and related edge information E(E == e(2)) = e(1); E(k,:) = []; cost(k,:) = []; Qbar(:,:,k) = []; v(:,:,k) = []; % delete duplicate edge and related edge information [E,ia,ic] = unique(sort(E,2), 'rows'); cost = cost(ia,:); Qbar = Qbar(:,:,ia); v = v(:,:,ia); % pairs involving v1 pair = sum(E == e(1), 2) > 0; npair = sum(pair); % updata edge information Qbar(:,:,pair) = Q(:,:,E(pair,1)) + Q(:,:,E(pair,2)); pair_v1 = permute([V(E(pair,1),:),ones(npair,1)], [2,3,1]); pair_v2 = permute([V(E(pair,2),:),ones(npair,1)], [2,3,1]); pair_vm = 0.5 .* (pair_v1 + pair_v2); v(:,:,pair) = [pair_v1, pair_v2, pair_vm]; cost(pair,1) = sum(squeeze(sum(bsxfun(@times,pair_v1,Qbar(:,:,pair)),1)).*squeeze(pair_v1),1)'; cost(pair,2) = sum(squeeze(sum(bsxfun(@times,pair_v2,Qbar(:,:,pair)),1)).*squeeze(pair_v2),1)'; cost(pair,3) = sum(squeeze(sum(bsxfun(@times,pair_vm,Qbar(:,:,pair)),1)).*squeeze(pair_vm),1)'; fprintf('%d\n', i); end clf drawMesh(V, F, 'facecolor','y', 'edgecolor','k', 'linewidth', 1.2); view([0 90]) axis equal axis off camlight lighting gouraud cameramenu
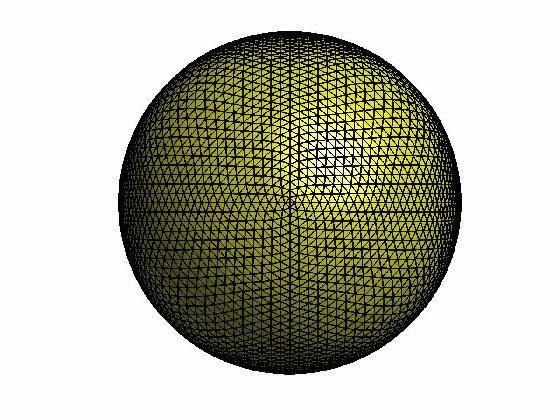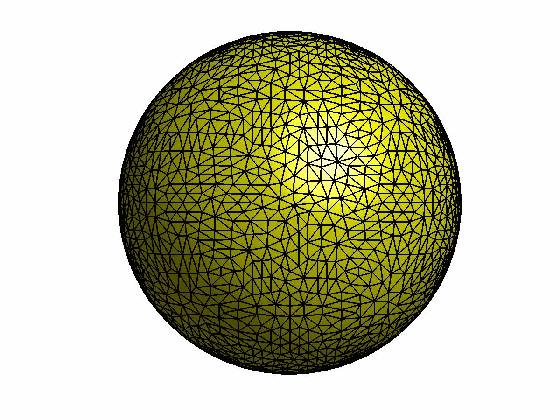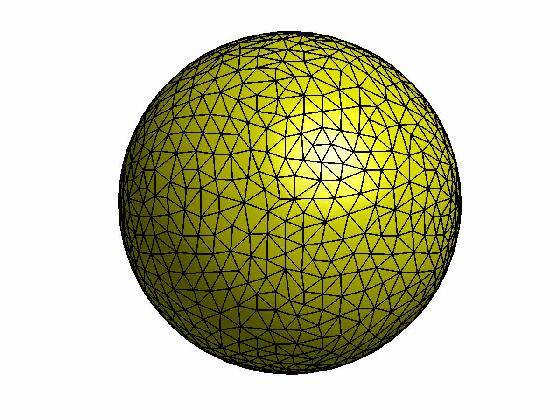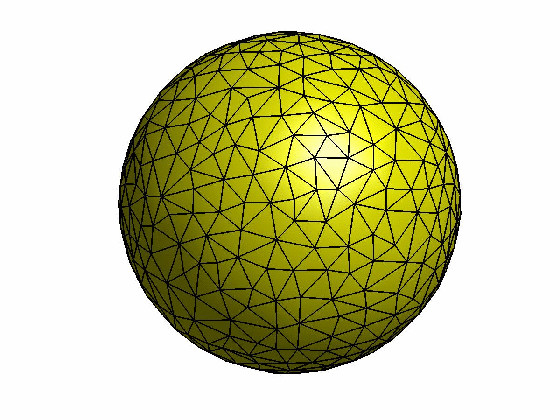
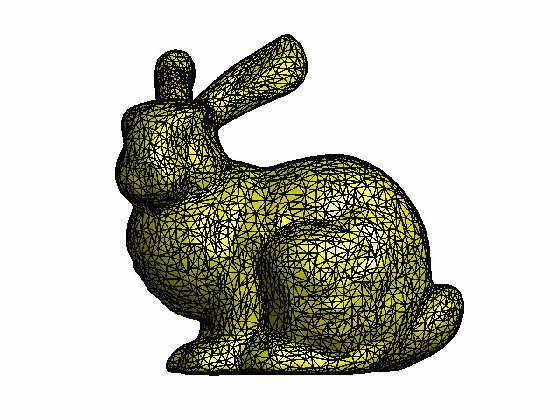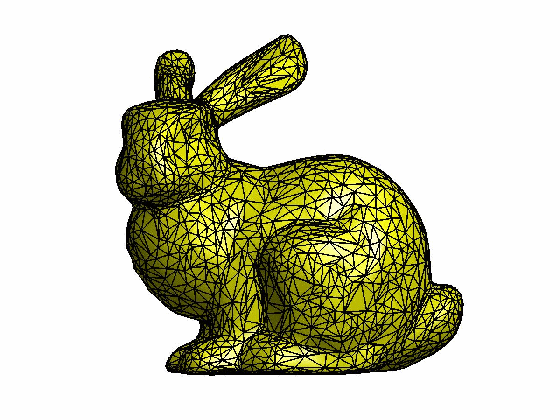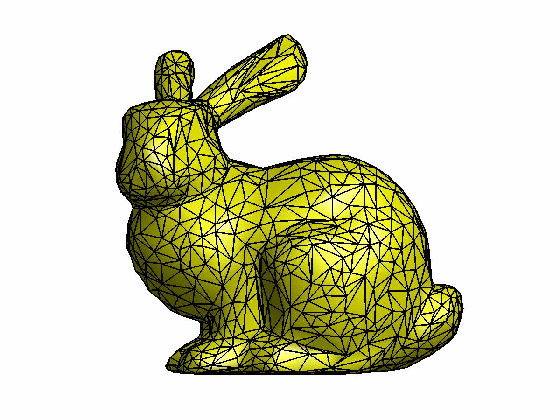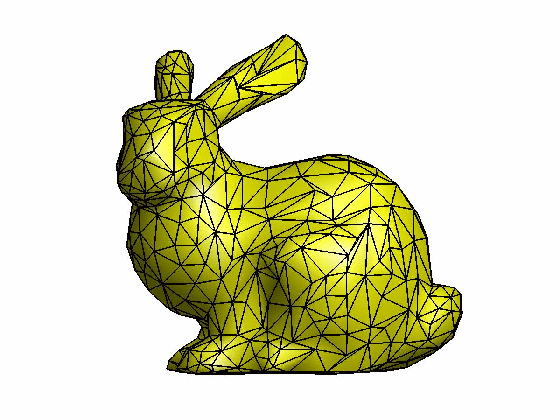
本文为原创,转载请注明出处:http://www.cnblogs.com/shushen
参考文献:
[1] Michael Garland and Paul S. Heckbert. 1997. Surface simplification using quadric error metrics. In Proceedings of the 24th annual conference on Computer graphics and interactive techniques (SIGGRAPH '97). ACM Press/Addison-Wesley Publishing Co., New York, NY, USA, 209-216.





 浙公网安备 33010602011771号
浙公网安备 33010602011771号