(转) 二叉树常见面试题2
本文整理自:https://www.cnblogs.com/33debug/p/7252371.html
一、常见题型
1. 求两个节点的最近公共祖先;
2. 求二叉树中最远的两个节点的距离;
3. 由前序遍历和中序遍历重建二叉树(如:前序序列:1 2 3 4 5 6 - 中序序列 :3 2 4 1 6 5);
4. 判断一棵树是否是完全二叉树 ;
5. 将二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点,只能调整树中结点指针的指向;
6.求二叉树的宽度;
7. 判断一棵二叉树是否是平衡二叉树;
8.判断一颗二叉树是否是另一颗树的子树。
二、解题思路分析
1.两个节点的最近公共祖先
求两个节点的最近公共祖先可分为三种情况,分别为:
(1)搜索二叉树,根据搜索二叉树的性质,左子树的所有节点比根节点小,右子树的所有节点比跟节点大。
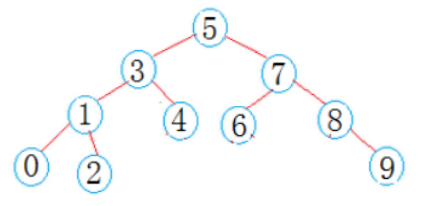
如果两个节点都比根节点小,则递归左子树 ;
如果两个节点都比跟节点大,则递归右子树 ;
否则,两个节点一个在左子树,一个在右子树,则当前节点就是最近公共祖先节点。
Node* GetAncestor(Node* root, Node* x1, Node* x2)//1.该二叉树为搜索二叉树 { assert(x1 && x2); if (x1->_data <= root->_data && x2->_data <= root->_data) { return GetAncestor(root->_left, x1, x2);//两个节都小于根节点,最近公共祖先在左子树中 } else if (x1->_data > root->_data && x2->_data > root->_data) { return GetAncestor(root->_right, x1, x2);//两个节都大于根节点,最近公共祖先在左子树中 } else return root; //一个在左子树,一个在右子树,找到公共祖先 }
(2)三叉链,二叉树节点有指向父节点的指针。
给定的两个节点都含有父节点,因此,可将这两个节点看做是两个链表的头结点,将求两个节点的最近公共祖先节点转化为求两链表的交点,这两个链表的尾节点都是根节点。
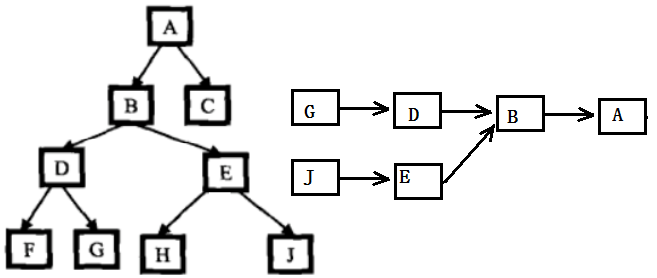
int Hight(BinaryNode* root, BinaryNode* node) { int len = 0; for (; node != NULL; node = node->_parent) len++; return len; } BinaryNode* GetLastCommonAncestor(BinaryNode* root, BinaryNode* node1, BinaryNode* node2) { if (root == NULL || node1 == NULL || node2==NULL) return NULL; int len1 = Hight(root,node1); int len2 = Hight(root,node2); for (; len1 > len2; len1--) node1 = node1->_parent; for (; len2 > len1; len2--) node2 = node2->_parent; while (node1 && node2 && node1 != node2) { node1 = node1->_parent; node2 = node2->_parent; } if (node1 == node2) return node1; else return NULL; }
3)普通二叉树
下面的方法时间复杂度为O(N),但是需要额外的空间来存储路径。
1) 找到从根到node1的路径,并存储在一个向量或数组中。
2)找到从根到node2的路径,并存储在一个向量或数组中。
3) 遍历这两条路径,直到遇到一个不同的节点,则前面的那个即为最低公共祖先.
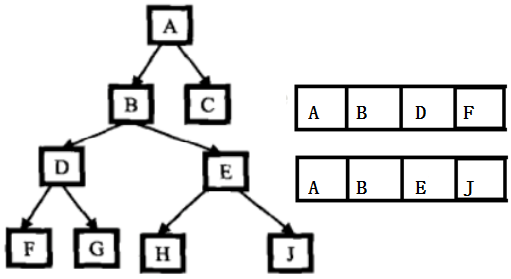
bool GetNodePaths(Node* root, Node* node, stack<Node *>& s) { if (root == NULL) { return false; } s.push(root); if (root == node) { return true; } bool inleft = GetNodePaths(root->_left, node, s); if (inleft) { return true; } bool inright = GetNodePaths(root->_right, node, s); if (inright) { return true; } s.pop(); return false; } Node* GetAncestor(Node* root, Node* x1, Node* x2); { assert(x1 && x2); stack<Node*> paths1, paths2; if (!GetNodePaths(root->_left, x1, paths1) || !GetNodePaths(root->_right, x2, paths2)) { return NULL; } else{ while(paths1.size()>paths2.size()){ paths1.pop(); } while(paths1.size()<paths2.size()){ paths2.pop(); } while(!paths1.empty() && !paths2.empty() && paths1.top()!=paths2.top()){ if(paths1.top()==paths2.top()) return paths1.top(); paths1.pop(); paths2.pop(); } } return NULL; }
2.最远的两个节点的距离
第一种情况最远的两个节点的距离为它们到根节点的路径长度之和,又有可能距离最远的两个节点之间的路径不经过根节点,如图所示:
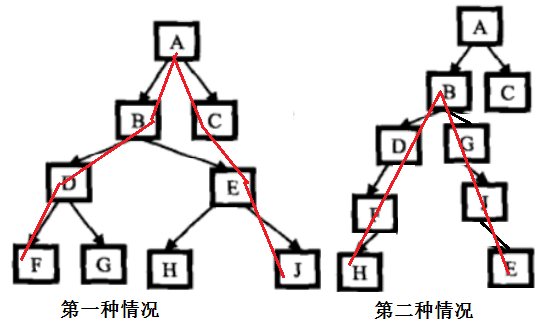
时间复杂度为O(N)的解法:
size_t _MaxLen(Node* root, size_t maxlen) //O(N) { if (root == NULL) { return; } size_t left = _MaxLen(root->_left, maxlen); size_t right = _MaxLen(root->_right, maxlen); if (right+left>maxlen) { maxlen = right + left; } return left > right ? left + 1 : right + 1; }
3. 前序遍历和中序遍历重建二叉树
这个题是要用一颗二叉树的前序遍历序列和中序遍历序列,如:前序序列:1 2 3 4 5 6 - 中序序列 :3 2 4 1 6 5,来重新构建二叉树。可以利用前序序列和中序序列中根节点的位置特性作为重建依据。图示解析过程如下:
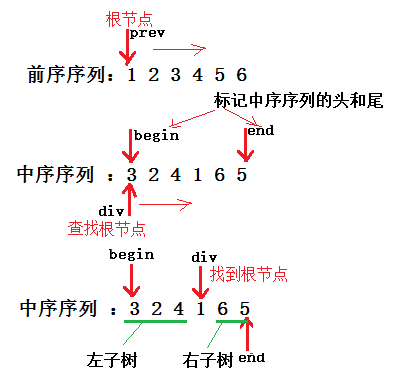

创建右子树的方法与左子树的方法完全相同。当 prev 遍历完前序序列,即二叉树创建完成。代码如下:
//由前序遍历和中序遍历重建二叉树(如:前序序列:1 2 3 4 5 6 - 中序序列 :3 2 4 1 6 5) Node* RebulidTree(char* prev, char* inbgein, char* inend) { assert(prev && inbgein && inend); if (inbgein > inend || prev == '\0') { return NULL; } Node* root = new Node(*prev); //先创建根节点 char* div = inbgein; //让div查找根节点 while (div <= inend) { if (*div == *prev) { if (inbgein <= div -1) { root->_left = RebulidTree(++prev, inbgein, div - 1);//递归创建左子树 } else { root->_left = NULL; } if (div + 1 <= inend) { root->_right = RebulidTree(++prev, div + 1, inend);//递归创建右子树 } else { root->_right = NULL; } break; } ++div; } return root; }
4. 判断一棵树是否是完全二叉树
完全二叉树: 前n-1层都是满的,第n层如有空缺,则是缺在右边,即第n层的最右边的节点,它的左边是满的,右边是空的。
这是一个层序遍历非递归法的变型题,同样要借助额外空间来临时存储节点。按照层序遍历二叉树,找到第一个只有非满结点(这个节点只有两种情况,孩子为空或者只有左没有右),如果之后的节点还有非满结点,则不是。
bool IsComplateTree(Node* root) { queue<Node*> q; if (root) { q.push(root); //先将节点压入队列中 } //这里给一个tag是标记是否出现非满节点 bool tag = true; while (!q.empty()) { Node* front = q.front(); q.pop(); //如果已经出现过非满结点,则后面再出现有孩子的结点则一定不是完全二叉树。 if (front->_left) { if (tag == false) { return false; } q.push(front->_left); } else { tag = false; } if (front->_right) { if (tag == false) { return false; } q.push(front->_right); } else { tag = false; } } return true; }
第二种思路:将所有的结点全部押入队列中,每次判断队列的头如果队列头为空了则跳出循环,如果此后队列中还有元素则不是完全二叉树。
bool IsCompleteTree(BinaryTreeNode *pRoot) { if(pRoot == NULL) return false; queue<BinaryTreeNode*> q; q.push(pRoot); BinaryTreeNode* pCur = q.front(); while(pCur != NULL) { q.pop(); q.push(pCur -> left); q.push(pCur -> right); pCur = q.front(); } q.pop();//把空pop出来 //因为以经有一个空了,所以只要头不为空就不是完全二叉树 while(! q.empty()) { if(q.front() != NULL) return false; q.pop(); } return true; }
5. 将二叉搜索树转换成一个排序的双向链表
void _ToList(Node* cur, Node*& prev) { if (cur == NULL) return; _ToList(cur->_left, prev); // cur->_left = prev; if(prev) prev->_right = cur; prev = cur; _ToList(cur->_right, prev); } Node* ToList(Node* root) { Node* prev = NULL; _ToList(root, prev); Node* head = root; while (head && head->_left) { head = head->_left; } return head; }
6.求二叉树的宽度
所谓二叉树的宽度是指:二叉树各层节点个数的最大值。
我们知道层序遍历二叉树是使用 queue 来实现的:每次打印一个节点之后,如果存在左右子树,则把左右子树压入 queue,那么此时的队列中可能既包含当前层的节点,也包含下一层的节点。
而我们要求的是对于特定某一层的节点的个数,因此我们需要从头结点开始,记录每一层的个数,对于当前层的每一个节点,在弹出自身之后把其左右子树压入 queue,当把当前层全部弹出队列之后,在队列中剩下的就是下一层的节点。然后比较队列的size和之前得到的maxWidth,取最大值即为队列的宽度。最终队列为空,得到的maxWidth就是二叉树的宽度!
int Width(Node* root) { queue<Node*> q; if (root) q.push(root); int maxwidth = 1; while (!q.empty()) { int length = q.size(); while (length-- > 0) { Node* front = q.front(); q.pop(); if (front->_left) { q.push(front->_left); } if (front->_right) { q.push(front->_right); } } maxwidth = maxwidth > q.size() ? maxwidth : q.size(); } return maxwidth; }
7. 二叉树是否是平衡二叉树
二叉树中每一个节点的左右子树高度之差均小于2即为平衡二叉树。那么当一颗二叉树的所有子树都是平衡二叉树时,它本身必定为平衡二叉树,用此思想可递归判断二叉树是否是平衡二叉树。代码如下:
//--判断一棵二叉树是否是平衡二叉树 bool IsBalance(Node* root) //O(N^2) { if (root == NULL) { return false; } int left = Depth(root->_left); int right = Depth(root->_right); return abs(right - left) < 2 && IsBalance(root->_left) && IsBalance(root->_right); }
这种方法借助左右的高度比较来确定是否为二叉树,需多次遍历二叉树,时间复杂度为O(N^2)。下面是一种O(N)的算法:
bool IsBalance(Node* root, int& depth) //O(N) { if (root == NULL) { depth = 0; return true; } int leftdepth = 0; if (IsBalance(root->_left, leftdepth) == false) { return false; } int rightdepth = 0; if (IsBalance(root->_right, rightdepth) == false) { return false; } depth = rightdepth > leftdepth ? rightdepth + 1 : leftdepth + 1; return abs(leftdepth - rightdepth) < 2; }
8.二叉树是否为另一颗树的子树
判断一颗二叉树是否是另一颗树的子树。
先在找二叉树里找根节点,找到之后判断后续的节点是否相等,如果相等,则为子树。
bool JudgeNextTree(Node* next, Node* child) //两棵树的起始节点的值已经相等,在判断其他节点是否相等 { if (child == NULL) { return true; } if (next == NULL) { return false; } if (next->_data == child->_data) // { return JudgeNextTree(next->_left, child->_left) && JudgeNextTree(next->_right, child->_right); } else { return false; //如果左右孩子都相等,则是子树,否则不是 } } bool JudgeTree(Node* parent, Node* child) //判断child是否为parent的子树 { if (child == NULL) //空树是任何树的子树 { return true; } if (parent == NULL) //空树没有除空树的任何子树 { return false; } if (parent->_data == child->_data) //当前节点与要查找子树的根节点相同时 { return JudgeNextTree(parent, child); //从相等节点开始判断是否为子树 } else if (JudgeTree(parent->_left, child->_left) == true) //判断当前节点的左子树是否与要查找子树的根节点相同 { return true; } else { return JudgeTree(parent->_right, child->_right); //判断当前节点的右子树是否与要查找子树的根节点相同 } }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号