《操作系统导论》第9章 | 比例份额调度

在本章中，我们来看一个不同类型的调度程序——比例份额（proportional-share）调度程序，有时也称为公平份额（fair-share）调度程序。比例份额算法认为，调度程序的最终目标是确保每个工作获得一定比例的CPU时间，而不是优化周转时间和响应时间。它的基本思想很简单：每隔一段时间，都会举行一次彩票抽奖，以确定接下来应该运行哪个进程。越是应该频繁运行的进程，越是应该拥有更多地赢得彩票的机会。关键的问题就是，如何设计调度程序来按比例分配CPU？

使用彩票数表示份额

在彩票调度中，彩票数代表了进程占有某个资源的份额。一个进程拥有的彩票数占总彩票数的百分比，就是它占有资源的份额。假设有两个进程A和B，A拥有75张彩票，B拥有25张。因此我们希望A占用75%的CPU时间，而B占用25%。

通过不断且定时地抽取彩票，彩票调度从概率上获得这种份额比例。抽取彩票的过程很简单：调度程序知道总共的彩票数（在我们的例子中，有100张）。调度程序抽取中奖彩票，这是从0和99之间的一个数，拥有这个数对应的彩票的进程中奖。假设进程A拥有0到74共75张彩票，进程B拥有75到99的25张，中奖的彩票就决定了运行A或B。调度程序然后加载中奖进程的状态，并运行它。彩票调度利用了随机性，这导致了从概率上满足期望的比例。随着这两个工作运行得时间越长，它们得到的CPU时间比例就会越接近期望。

随机方法相对于传统的决策方式，至少有3点优势。第一，随机方法常常可以避免奇怪的边角情况，较传统的算法（LRU替换策略）可能在处理这些情况时遇到麻烦。虽然LRU通常是很好的替换算法，但在有重复序列的负载时表现非常差。随机方法就没有这种最差情况。

第二，随机方法很轻量，几乎不需要记录任何状态。在传统的公平份额调度算法中，记录每个进程已经获得了多少的CPU时间，需要对每个进程计时，这必须在每次运行结束后更新。而采用随机方式后每个进程只需要非常少的状态（即每个进程拥有的彩票号码）。

第三，随机方法很快。只要能很快地产生随机数，做出决策就很快。因此，随机方式在对运行速度要求高的场景非常适用。当然，越是需要快的计算速度，随机就会越倾向于伪随机。

彩票机制

彩票调度还提供了一些机制，以不同且有效的方式来调度彩票。一种方式是利用彩票货币（ticket currency）的概念。这种方式允许拥有一组彩票的用户以他们喜欢的某种货币，将彩票分给自己的不同工作。之后操作系统再自动将这种货币兑换为正确的全局彩票。

比如，假设用户A和用户B每人拥有100张彩票。用户A有两个工作A1和A2，他以自己的货币，给每个工作500张彩票（共1000张）。用户B只运行一个工作，给它10张彩票（总共10张）。操作系统将进行兑换，将A1和A2拥有的A的货币500张，兑换成全局货币50张。类似地，兑换给B1的10张彩票兑换成100张。然后会对全局彩票货币（共200张）举行抽奖，决定哪个工作运行。

User A -> 500 (A's currency) to A1 ->  50 (global currency)
       -> 500 (A's currency) to A2 ->  50 (global currency)
User B ->  10 (B's currency) to B1 -> 100 (global currency)

另一个有用的机制是彩票转让（ticket transfer）。通过转让，一个进程可以临时将自己的彩票交给另一个进程。这种机制在客户端/服务端交互的场景中尤其有用，在这种场景中，客户端进程向服务端发送消息，请求其按自己的需求执行工作，为了加速服务端的执行，客户端可以将自己的彩票转让给服务端，从而尽可能加速服务端执行自己请求的速度。服务端执行结束后会将这部分彩票归还给客户端。

最后，彩票通胀（ticket inflation）有时也很有用。利用通胀，一个进程可以临时提升或降低自己拥有的彩票数量。当然在竞争环境中，进程之间互相不信任，这种机制就没什么意义。一个贪婪的进程可能给自己非常多的彩票，从而接管机器。但是，通胀可以用于进程之间相互信任的环境。在这种情况下，如果一个进程知道它需要更多CPU时间，就可以增加自己的彩票，从而将自己的需求告知操作系统，这一切不需要与任何其他进程通信。

实现

彩票调度实现起来非常简单，只需要一个随机数生成器来选择中奖彩票和一个记录系统中所有进程的数据结构，以及所有彩票的总数。假设我们使用列表记录进程，下面的例子中有A、B和C这3个进程，每个进程有一定数量的彩票。

在做出调度决策之前，首先要从彩票总数400中选择一个随机数。假设这里选择了300，然后我们遍历链表，用一个计数器帮我们找到这个数字。

// counter: used to track if we've found the winner yet
int counter = 0;

// winner: use some call to a random number generator to
//         get a value, between 0 and the total # of tickets
int winner = getrandom(0, totaltickets);

// current: use this to walk through the list of jobs
node_t *current = head;

// loop until the sum of ticket values is > the winner
while (current) {
  counter = counter + current->tickets;
  if (counter < winner) break;  // found the winner
  current = current->next;
}  // 'current' is the winner: schedule it...

这段代码从前向后遍历进程列表，将每张票的值加到counter上，直到值超过winner。这时，当前的列表元素所对应的进程就是中奖者。在我们的例子中，中奖彩票是300。首先，计A的票后，counter增加到100。因为100小于300，继续遍历。然后counter会增加到150（B的彩票），仍然小于300，继续遍历。最后，counter增加到400（显然大于300），因此退出遍历，current指向C（中奖者）。一个更有效率的做法是将列表项按照彩票数递减排序。这个顺序并不会影响算法的正确性，但能保证用最小的迭代次数找到需要的节点，尤其当大多数彩票被少数进程掌握时。

一个例子

为了更好地理解彩票调度的运行过程，我们现在简单研究一下两个互相竞争工作的完成时间，每个工作都有相同数目的100张彩票，以及相同的运行时间\(R\)，我们希望两个工作在大约同时完成，由于彩票调度算法的随机性，有时一个工作会先于另一个完成。为了量化这种区别，我们定义了一个简单的不公平指标\(U\)（unfairness metric），将两个工作完成时刻相除得到\(U\)的值。比如，运行时间\(R\)为10，第一个工作在时刻10完成，另一个在20，那么\(U=10/20=0.5\)。如果两个工作几乎同时完成，\(U\)的值将很接近于1。因此，完美的公平调度程序可以做到\(U=1\)。

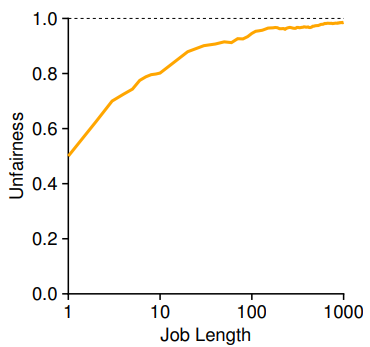
上图展示了当两个工作的运行时间从1到1000变化时，30次试验的平均\(U\)值。可以看出，当工作执行时间很短时，平均不公平度非常糟糕。只有当工作执行非常多的时间片时，彩票调度算法才能得到期望的结果。

如何分配彩票

关于彩票调度的一个关键问题就是如何为工作分配彩票？这是一个非常棘手的问题，系统的运行严重依赖于彩票的分配。假设用户自己知道如何分配，因此可以给每个用户一定量的彩票，由用户按照需要自主分配给自己的工作。然而这种方案似乎什么也没有解决——还是没有给出具体的分配策略。因此对于给定的一组工作，彩票分配的问题依然没有最佳答案。

步长调度

步长调度也很简单。系统中的每个工作都有自己的步长，这个值与票数值成反比。在上面的例子中，A、B、C这3个工作的票数分别是100、50和250，我们通过用一个大数分别除以他们的票数来获得每个进程的步长。比如用10000除以这些票数值，得到了3个进程的步长分别为100、200和40。我们称这个值为每个进程的步长（stride）。每次进程运行后，我们会让它的计数器（称为行程值）增加它的步长，记录它的总体进展。

current = remove_min(queue);       // pick client with minimum pass
schedule(current);                 // use resource for quantum
current->pass += current->stride;  // compute next pass using stride
insert(queue, current);            // put back into the queue

在我们的例子中，3个进程（A、B、C）的步长值分别为100、200和40，初始行程值都为0。因此，所有进程都可能被选择执行。假设选择A，A执行一个时间片后，更新它的行程值为100。然后运行B，并更新其行程值为200。最后执行C，C的行程值变为40。这时，算法选择最小的行程值，是C，执行并增加为80（C的步长是40）。然后C再次运行（依然行程值最小），行程值增加到120。现在运行A，更新它的行程值为200（现在与B相同）。然后C再次连续运行两次，行程值也变为200。此时，所有行程值再次相等，这个过程会无限地重复下去。下表展示了一段时间内调度程序的行为。

可以看出，C运行了5次、A运行了2次，B运行了1次，正好是票数的比例——200、100和 50。彩票调度算法只能一段时间后，在概率上实现比例，而步长调度算法可以在每个调度周期后做到完全正确。

既然有了可以精确控制的步长调度算法，为什么还要彩票调度算法呢？相比于步长调度，彩票调度的优势是不需要全局状态。假如一个新的进程在步长调度执行过程中加入系统，应该怎么设置它的行程值呢？设置成0吗？这样的话，它就独占CPU了。而彩票调度算法不需要对每个进程记录全局状态，只需要用新进程的票数更新全局的总票数就可以了。因此彩票调度算法能够更合理地处理新加入的进程。

本章介绍了比例份额调度的概念，并简单讨论了两种实现：彩票调度和步长调度。彩票调度通过随机值做到了按比例分配；步长调度算法能够确定的获得需要的比例。然而两者并没有作为CPU调度程序被广泛使用。一个原因是这两种方式都不能很好地适合I/O；另一个原因则是票数分配问题并没有确定的解决方式。因此，比例份额调度程序只有在这些问题可以相对容易解决的领域更有用。例如在虚拟数据中心中，我们可能会希望分配1/4的CPU周期给Windows虚拟机，剩余的给Linux系统，比例分配的方式可以更简单高效。