CVPR'23-HumaniFlow工作总结
概述:通过对HumaniFlow工作的介绍,期望各位能建立起对3D人体姿势估计和建模分布的知识体系,并且能够讲这一部分知识迁移到未来的实验中。我们在这里做一个抛砖引玉的工作,把我们所知道的尽可能传递给大家。第一次做系列视频难免经验不足,如果有不理解的地方欢迎相互交流,我们共同进步!
对于一项顶会工作,我们的目标是充分挖掘两点:
- 两个“点”:出发点和亮点
- 两个“思想”:核心思想和延伸的思想
那么,对于本文章而言,通过摘要能得到很多信息。
ABSTRACT
摘要提到第一个词:单目3D人体姿势和形态估计(Monocular 3D...)。这里请注意一个词,“单目”,表示我们只有一个摄像头/单机位,反映到实验过程中就是只有来自一个视角的图片。通过调研发现,单目的pose tracking技术由于已知信息的稀少,是一个极具挑战性的课题。但如果一旦解决这一大难题,将有机会应用到各个行业:赛事直播模拟、医学体态纠正、动作仿真实验等,因此其研究潜力十足。挑战性带来研究上的瓶颈,具体来说,我们发现大多数工作会陷入一个“不可能三角”——三个指标之间会彼此约束,无法同时提高。举个简单的例子,在经济市场中,商品价格越高,需求量往往会越低;反之亦然。我们发现在sample-input consistency/sample diversity/accuracy三者也存在类似的关系。
- Sample-Input Consistency:(3D samples from predicted distribution)<-->(2D ground truth input)
- Sample Diversity:样本多样性(用于提高泛化能力)
- Accuracy(acc): 预测精度(很简单,用一个条件概览表示:P(3D ground truth|predicted distribution))
三个指标之间存在什么关系?
三个指标的出发点很简单,可以简化为已知和未知的关系。
- 对于已知数据集,我们期望模型预测效果越好:这部分由 Acc 和 Consistency刻画
- 对于未知数据集,我们期望模型具有同样效果,或者,至少精度损失尽可能小->泛化能力:这部分由 Diversity 刻画
因此,“不可能三角”出现的原因就显而易见了:模型在过拟合和欠拟合之间存在一个平衡点。现有模型可能对于更复杂的数据集毫无办法,泛化能力不如预期,比如in-the-wild数据集。这些数据集不同于学术界的benchmark,具有高度的不一致性,存在遮挡/截断/(深度)模糊。
为了解决以上问题,打破指标之间的“平衡”,这个团队做了什么工作?
受到VAE和SMPL(稍后介绍)启发,剑桥三剑客团队提出了一种全新的架构用于该领域。概括来说,一个人被模型划分成几个局部,举个例子,肩膀往下是一个局部,胯部往下是一个局部。局部之间存在依赖关系,很多动作实际上是复合的,多关节共同旋转/移动,因此需要引入一种表征模型来刻画这种局部依赖关系:SMPL运动学树——一种天然的树形结构:对一个非根节点,父节点与子节点相连,学过数据结构的同学知道,子节点的更新可以通过根路径向上传递,父节点同理。因此,局部依赖问题解决了。仅依靠SMPL肯定不足以预测关节旋转分布,模型复杂度太低,HumaniFlow的思路是通过产生更多的关节分布candidate,生成大量有效数据来扩充SMPL的训练质量,在此基础上提高预测质量,进一步提高算法的鲁棒性和泛化能力。
VAE核心思想:观测数据->得到表达式,近似分布->利用表达式->数据变换/数据生成。
如何获得表达式?根据近似原理,神经网络可以拟合任意次数的函数,对于一个变量的分布,通过不断拆分成变量和噪声变量的组合,可以达到目的。
SMPL核心思想:我把SMPL比喻成一个可调节的人体模型,就像玩具人一样。这个模型有一个固定的平均形态,就像玩具人的初始状态。然后,通过对模型进行调整,我们可以改变它的姿势和外形,就好像按动玩具人的关节,让它摆出不同的姿势一样。
SMPL = 骨架结构 + 皮肤表面,两部分均可参数化->可调节->表达能力强,适用现实复杂情境。SMPL模型使用了一组参数,包括全局旋转参数、关节角度参数、身体尺度参数等。这些参数的值会影响到模型的姿态和形状。通过改变这些参数的值,我们可以在低维参数空间中探索不同的姿态和形态,然后将参数映射回三维空间,生成对应的人体模型。(2D-潜在空间->3D-空间,映射思想)
共同核心思想:它们的核心思想都是将数据映射到低维潜在空间中,并利用该空间进行数据的表示、生成和变换。VAE主要用于对一般数据分布进行建模,可以在各种应用场景中进行数据重构和生成。而SMPL主要用于对人体姿态和形态进行建模。
Normalizing Flows + SMPL
更可控的姿态生成:SMPL是一个基于线性代数的参数化人体模型,它通过控制身体的关节角度、肢体长度和姿态来生成不同的人体形态。而归一化流可以学习到将先验分布转换为目标分布的变换函数,只要给定相应的随机向量,就可以生成与目标分布相符合的新样本。通过结合SMPL和归一化流,我们可以更加准确地控制姿态生成的过程,使生成的人体形态更加符合实际需求。
更高质量的姿态重建:SMPL可以从RGB图像或深度图像中估计出人体的姿态和形态,但由于噪声、遮挡等因素的影响,重建质量可能会受到限制。而归一化流可以对输入图像进行去噪、对齐和增强等操作,从而提高姿态重建的精度和准确度。此外,归一化流还可以通过生成大量有效数据来扩充SMPL的训练集,进一步提高姿态重建的鲁棒性和泛化能力。
更广泛的应用场景:结合归一化流可以扩展SMPL的应用场景,比如虚拟试衣、人体动画和运动捕捉等领域。由于归一化流具有概率密度估计和采样能力,可以在SMPL的基础上生成更加丰富和逼真的人体形态,从而支持更广泛的应用场景。
总结来说,归一化流“增加有效数据,减少无效数据”,赋能SMPL训练过程。
这就是摘要的主要内容
RELATED WORK
两个关键词:单目估计(姿势+形态)和3D情境估计(姿势+形态)
单目估计
两个情境:面向参数(optimization-based)和面向机理(learning-based);
前者根据模型参数和损失函数(consistency),迭代优化,得到一个有效的模型;后者关注如何高效地表示和学习潜在特征,对于如何表示:在3D重建领域有四种常见的数据形式:网格(grid)/点云(point set)/体素(mesh)/深度图(depth graph); 对于如何学习,借助深度学习的原理,比如DNN网络具有天然的捕捉图像特征的能力。
3D情境的估计
两个阶段:早期是leraning-based,现阶段以optimization-based为主。具体地,研究工作的演化
mixture density networks/normalising flows -> body-part rotations -> categorical distribution over SMPL( pose+shape params): Gaussian/Hierarchical matrix-Fisher distribution over body-part rotations -> ProHMR adopts addictive coupling normalising flows -> more expressive distributions over SMPL.
总结:存在“不可能三角”关系
METHOD
Normalising Flows
目的:Normalizing flow是一种基于可微变换的生成模型,可以通过一系列的可逆变换将一个简单的噪声分布映射为目标分布,从而实现对目标分布进行采样、计算概率密度等操作。
下面是normalizing flow的公式表示:
假设我们有一个简单的随机噪声分布 \(p_z(z)\),希望使用一个可逆的函数变换 \(f\) 将其映射为一个复杂的目标分布 \(p_x(x)\),即 \(x=f(z)\)。如果 \(f\) 是可逆的,那么我们可以通过反向变换 \(z=f^{-1}(x)\) 计算目标分布的概率密度:
其中,\(\det \frac{\partial f^{-1}(x)}{\partial x}\) 表示反向变换的雅可比行列式,用来衡量在 \(x\) 点的微小变化在 \(z\) 空间中所占据的体积大小。比如,在正交矩阵的变换下,雅可比行列式的值为 1。
为了构建一个更复杂的生成模型,我们可以使用多个可逆变换组合起来,形成一个 normalizing flow。具体来说,设 \(z_0\) 为噪声分布采样得到的初始样本,\(z_K\) 为经过 \(K\) 次变换后得到的最终样本,那么整个 normalizing flow 可以表示为:
其中,每个变换 \(f_k\) 都是可逆的,可以是线性或非线性函数,形式化地表示为:
通过这些可逆变换,我们可以将噪声分布 \(p_z(z)\) 逐步映射为目标分布 \(p_x(x)\),从而实现对目标分布的采样、计算概率密度等操作。在实际应用中,常见的变换包括仿射变换、正交变换、卷积等。
总结:normalizing flow 是一种基于可逆变换的生成模型,通过将简单的噪声分布逐步映射为目标分布,实现对目标分布的采样和计算概率密度。
Lie Group Structure of \(SO(3)\)
目的:为什么需要SO(3)空间?
表示旋转:SO(3)是旋转矩阵的集合,因此将向量或矩阵映射到SO(3)空间可以方便地表示旋转操作。对于需要处理旋转的问题,如机器人运动规划、计算机视觉中的姿态估计等,将旋转表示为SO(3)中的元素更加直观和便捷。
保持结构:SO(3)作为一个Lie Group,具有一些良好的结构特性。通过将向量或矩阵映射到SO(3)空间,可以将原始数据保持在这种结构化的表示中,以便进行进一步的分析和处理。在优化问题中,使用SO(3)表示参数空间可以更好地保持旋转的约束和性质。
低冗余:SO(3)的维度是3,比原始向量或矩阵的维度低。通过将高维数据映射到SO(3)空间,可以去除一些冗余信息,从而减少数据的复杂性和计算的开销。这对于降维和数据压缩等任务很有帮助。
保持不变性:SO(3)空间具有旋转不变性,即对于两个等效的旋转操作,它们对应的旋转矩阵属于SO(3)中的同一个元素。因此,将向量或矩阵映射到SO(3)空间可以保持这种不变性特性,使得数据在进行旋转处理时更加稳定和可靠。
SO(3)的lie group结构的公式表示:
SO(3)是所有旋转三维空间的正交矩阵构成的集合。一个3x3的实数矩阵R属于SO(3)当且仅当满足以下条件:
- R的行列式为1: det(R) = 1
- R是正交矩阵: R^T * R = I (其中R^T表示R的转置矩阵,I表示单位矩阵)
我们可以使用旋转向量或欧拉角来表示SO(3)中的旋转。其中,旋转向量表示为一个三维向量ω=[ω₁, ω₂, ω₃],表示绕单位向量n=[n₁, n₂, n₃] 的方向旋转 |ω| 弧度。那么,对应的旋转矩阵 R 可以通过罗德里格斯公式(Rodrigues' formula)计算得到:
R = exp([ω]ₓ)
其中[ω]ₓ表示叉乘矩阵,即:
[ω]ₓ =
| 0 -ω₃ ω₂ |
| ω₃ 0 -ω₁ |
| -ω₂ ω₁ 0 |
exp([ω]ₓ)是指矩阵的指数函数,通过泰勒级数展开计算。
另一种常用的表示方式:欧拉角,其中ZYZ欧拉角是SO(3)中最通用的欧拉角参数化方法。在ZYZ欧拉角表示中,旋转矩阵R可以通过以下公式计算得到:
R = R₃(φ) R₂(θ) R₃(ψ)
其中R₃(φ),R₂(θ),R₃(ψ)分别表示绕Z轴旋转φ角度、绕Y轴旋转θ角度和绕Z轴旋转ψ角度的旋转矩阵。
总结:SO(3)是所有旋转三维空间的正交矩阵构成的集合,可以使用旋转向量或欧拉角来表示其中的旋转。旋转向量表示为一个三维向量,欧拉角则使用ZYZ欧拉角来参数化旋转矩阵。
SO(3)是一个连通紧致的、光滑的Lie群,其指数映射(exp)是满射,但不是单射,因此不是一个微分同胚。这是因为对于任何 \(\hat{u} \in so(3), k \in \mathbb{Z}\) 和整数 \(k\),都有 \(\exp(\hat{u}) = \exp((\theta + 2\pi k)\hat{k}^\wedge)\),其中 \(\theta\) 是旋转角度,\(\hat{k}\) 是任意单位向量。
给定一个旋转矩阵 \(R \in SO(3)\),可以使用对数算符(log)来计算相应的最小角度(axis-angle)向量 \(\theta \hat{u}\),其中 \(\theta\) 是旋转角度,\(\hat{u}\) 是旋转轴方向的单位向量。具体地,有 \(\theta \hat{u} = \text{log}(R)\),其中 log 表示对数算符。
在实际应用中,对数算符通常使用罗德里格斯公式(Rodrigues' formula)计算,即:
\(\text{log}(R) = \begin{cases} \theta \hat{u} & \sin\theta \neq 0 \\ \theta \hat{u} & \text{otherwise, any } \hat{u} \text{ satisfies } R = I \end{cases}\)
其中 \(\theta\) 可以通过以下公式计算得到:
\(\theta = \arccos\left(\frac{\text{tr}(R) - 1}{2}\right)\)
而旋转轴方向的单位向量 \(\hat{u}\),则可以通过以下公式计算得到:
\(\hat{u} = \begin{cases} \frac{1}{2\sin\theta} \begin{bmatrix} R_{32} - R_{23} \\ R_{13} - R_{31} \\ R_{21} - R_{12} \end{bmatrix} & \sin\theta \neq 0 \\ \hat{v} & \text{otherwise, any } \hat{v} \text{ satisfies } R = I \end{cases}\)
其中 \(R_{ij}\) 表示 \(R\) 的第 \(i\) 行、第 \(j\) 列的元素。


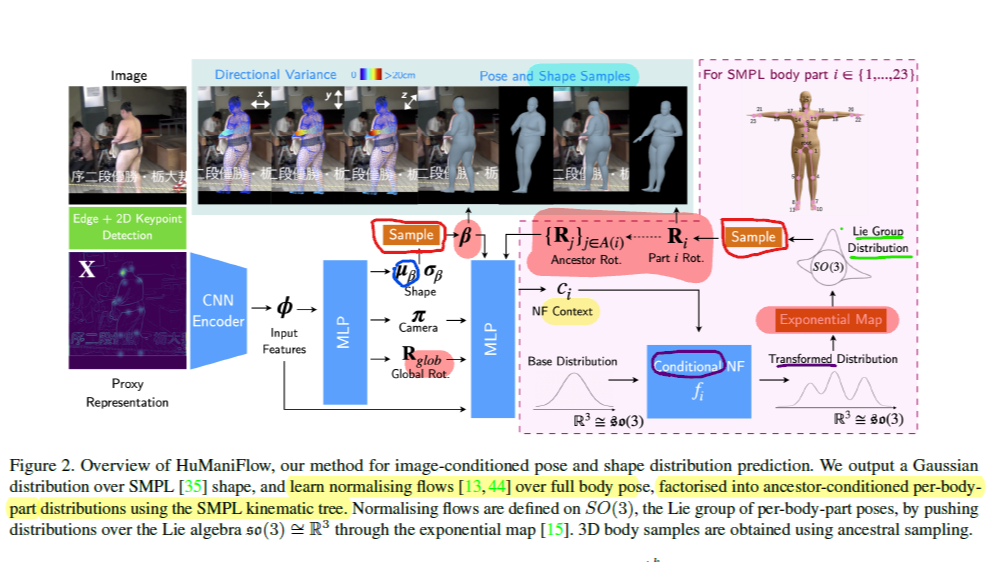 HumaniFlow文章总结工作
HumaniFlow文章总结工作

