大数据基础---机器学习与数据挖掘

前言

随着人工智能的发展，机器学习成为一个热门的学科。机器学习说白了就是利用一些数学知识，通过代码实现分类，聚类，特征提取和回归。这些所谓的实现也叫算法。

大部分算法已经有人帮我们写好了类库，我们只需要调用即可实现。

常用的实现类库有两个：一个是SparkMLlib，一个是Scikit-lean。

算法讲解

线性回归

什么是线性回归？

线性回归说白了就是利用大量结果，反推工程式。

多元线性回归:

多元线性回归就是有多个自变量，也就是多个未知数。

它的公式表示：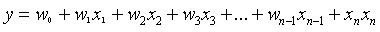

一元线性回归：

一元线性回归就是只有一个自变量。

它的公式表示：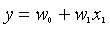

我们举个例子说明下一元线性回归：

比如有两组变量它们的x，y的值分别是x=3,y=5和x=6,y=8，那么可知如下：

5=w₀+w₁*3

8=w₀+w₁*6

可以求得w₀=2,w₁=1。

其中w₀称为截距，w₁称为斜率（有时也叫权重或者维度）。

如果一个图中有多个点，我们要找一条直线（构成这条直线的公式）来代表这些点之间的关系，那如何确定这条直线？

当每个点对应的y值和根据公式求得的y值之差的平方累加和最小时，这条直线就是最优解。这条直线这时就满足最小二乘法误差公式：

error=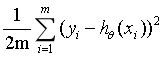

解释：

y_i代表的实际的值。

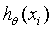代表的根据公式推测的y值。

m代表有m个离散点，前面的1/2是方便求导加上的，约去后面的平方。

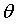表示权重w1,w2,w3...

error为0时代表没有误差，所有点都在一条直线上。当然，对于离散点来说，是不可能等于0的，我们要做的就是让error尽可能小。

那如何确定error的最小值呢？根据公式，我们可以把error看作是一个向上开头的图像。如下所示：

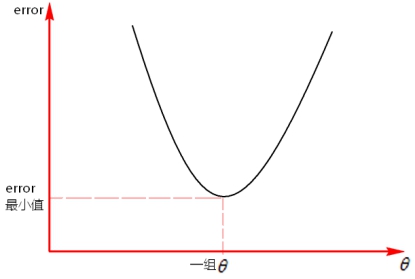
从图上可以看到当error处于最低点时是最优解。

通过求导的方式，理论上可以确定error的最小值，但是由于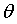是一组数据，无法确定error最小下对应的这一组权重 。

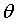正向的求导不能得到一组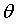权重值，就不能确定线性回归的公式。那么可以根据数据集来穷举法反向的试，来确定线性回归的公式。

根据穷举法求线性回归公式

• 已知有线性回归的训练集。

• 已知线性回归公式：

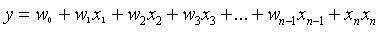
• 已知误差公式：

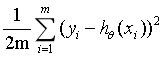
  这时我们可以设定一个初始模型，比如设定w₀=1，w₁=1，w₂=1…。这个时候我们就能求得误差值。

  我们在训练模型的时候，一般事先确定一个误差值，如果训练出的误差小于我们设置的误差，则停止训练，否则需要不断调节初始模型w₀，w₁，w₂…的步长（step），直到求得的error值小于我们设置的值时才停止。

  我画了个流程图大致如下：

  

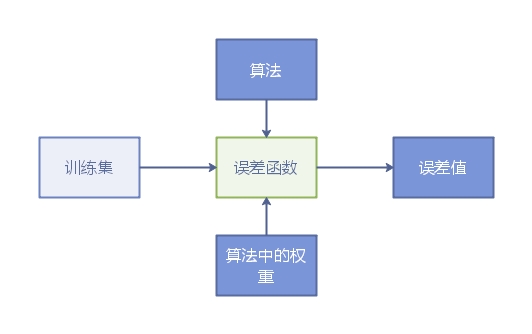
步长一般设定3的倍数，比如0.3,0.6,0.03,0.09等。

用梯度下降法调节权重

假设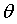和error的函数关系中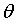，中只有一个维度w₀，那么这个关系其实就是w₀和error的关系，反应图上就是一维平面关系。如果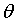中有两个维度w₀和w₁，那么这个反映到图上就是个三维空间关系，以此类推。

下面是个多维关系图：

如果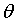中只有一个维度w₀，则表现如下：

在图中①，②，③，④，⑤，⑥，⑦都是图像的切线（斜率），在切点处可以求得对应的error值。如果沿着①->②->③方向调节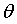和沿着④->⑤->⑥方向调节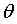，可以使error值更小。这种沿着斜率绝对值减少的方向，沿着梯度的负方向迭代调节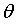的方法叫梯度下降法。

梯度下降法是找到权重最优解的一种方法。

过拟合和欠拟合

首先训练的数据一般会分为两部分，将80%的数据作为训练，20%的数据留作测试。

训练完毕后，将训练过的数据带入进去得到的误差值（error）很小，而将测试数据带入得到的误差值却很大，这种情况叫过拟合。

当带入训练数据和测试数据得到的误差都很大时，这个模型就很糟糕，这样的叫欠拟合。

Spark MLlib线性回归案例

训练数据集:

-0.4307829,-1.63735562648104 -2.00621178480549 -1.86242597251066 -1.02470580167082 -0.522940888712441 -0.863171185425945 -1.04215728919298 -0.864466507337306
-0.1625189,-1.98898046126935 -0.722008756122123 -0.787896192088153 -1.02470580167082 -0.522940888712441 -0.863171185425945 -1.04215728919298 -0.864466507337306
-0.1625189,-1.57881887548545 -2.1887840293994 1.36116336875686 -1.02470580167082 -0.522940888712441 -0.863171185425945 0.342627053981254 -0.155348103855541
-0.1625189,-2.16691708463163 -0.807993896938655 -0.787896192088153 -1.02470580167082 -0.522940888712441 -0.863171185425945 -1.04215728919298 -0.864466507337306
0.3715636,-0.507874475300631 -0.458834049396776 -0.250631301876899 -1.02470580167082 -0.522940888712441 -0.863171185425945 -1.04215728919298 -0.864466507337306
0.7654678,-2.03612849966376 -0.933954647105133 -1.86242597251066 -1.02470580167082 -0.522940888712441 -0.863171185425945 -1.04215728919298 -0.864466507337306
0.8544153,-0.557312518810673 -0.208756571683607 -0.787896192088153 0.990146852537193 -0.522940888712441 -0.863171185425945 -1.04215728919298 -0.864466507337306
1.2669476,-0.929360463147704 -0.0578991819441687 0.152317365781542 -1.02470580167082 -0.522940888712441 -0.863171185425945 -1.04215728919298 -0.864466507337306
1.2669476,-2.28833047634983 -0.0706369432557794 -0.116315079324086 0.80409888772376 -0.522940888712441 -0.863171185425945 -1.04215728919298 -0.864466507337306
1.2669476,0.223498042876113 -1.41471935455355 -0.116315079324086 -1.02470580167082 -0.522940888712441 -0.29928234305568 0.342627053981254 0.199211097885341
1.3480731,0.107785900236813 -1.47221551299731 0.420949810887169 -1.02470580167082 -0.522940888712441 -0.863171185425945 0.342627053981254 -0.687186906466865
1.446919,0.162180092313795 -1.32557369901905 0.286633588334355 -1.02470580167082 -0.522940888712441 -0.863171185425945 -1.04215728919298 -0.864466507337306
1.4701758,-1.49795329918548 -0.263601072284232 0.823898478545609 0.788388310173035 -0.522940888712441 -0.29928234305568 0.342627053981254 0.199211097885341
1.4929041,0.796247055396743 0.0476559407005752 0.286633588334355 -1.02470580167082 -0.522940888712441 0.394013435896129 -1.04215728919298 -0.864466507337306
1.5581446,-1.62233848461465 -0.843294091975396 -3.07127197548598 -1.02470580167082 -0.522940888712441 -0.863171185425945 -1.04215728919298 -0.864466507337306
1.5993876,-0.990720665490831 0.458513517212311 0.823898478545609 1.07379746308195 -0.522940888712441 -0.863171185425945 -1.04215728919298 -0.864466507337306
1.6389967,-0.171901281967138 -0.489197399065355 -0.65357996953534 -1.02470580167082 -0.522940888712441 -0.863171185425945 -1.04215728919298 -0.864466507337306
1.6956156,-1.60758252338831 -0.590700340358265 -0.65357996953534 -0.619561070667254 -0.522940888712441 -0.863171185425945 -1.04215728919298 -0.864466507337306
1.7137979,0.366273918511144 -0.414014962912583 -0.116315079324086 0.232904453212813 -0.522940888712441 0.971228997418125 0.342627053981254 1.26288870310799
1.8000583,-0.710307384579833 0.211731938156277 0.152317365781542 -1.02470580167082 -0.522940888712441 -0.442797990776478 0.342627053981254 1.61744790484887
1.8484548,-0.262791728113881 -1.16708345615721 0.420949810887169 0.0846342590816532 -0.522940888712441 0.163172393491611 0.342627053981254 1.97200710658975
1.8946169,0.899043117369237 -0.590700340358265 0.152317365781542 -1.02470580167082 -0.522940888712441 1.28643254437683 -1.04215728919298 -0.864466507337306
1.9242487,-0.903451690500615 1.07659722048274 0.152317365781542 1.28380453408541 -0.522940888712441 -0.442797990776478 -1.04215728919298 -0.864466507337306
2.008214,-0.0633337899773081 -1.38088970920094 0.958214701098423 0.80409888772376 -0.522940888712441 -0.863171185425945 -1.04215728919298 -0.864466507337306
2.0476928,-1.15393789990757 -0.961853075398404 -0.116315079324086 -1.02470580167082 -0.522940888712441 -0.442797990776478 -1.04215728919298 -0.864466507337306
2.1575593,0.0620203721138446 0.0657973885499142 1.22684714620405 -0.468824786336838 -0.522940888712441 1.31421001659859 1.72741139715549 -0.332627704725983
2.1916535,-0.75731027755674 -2.92717970468456 0.018001143228728 -1.02470580167082 -0.522940888712441 -0.863171185425945 0.342627053981254 -0.332627704725983
2.2137539,1.11226993252773 1.06484916245061 0.555266033439982 0.877691038550889 1.89254797819741 1.43890404648442 0.342627053981254 0.376490698755783
2.2772673,-0.468768642850639 -1.43754788774533 -1.05652863719378 0.576050411655607 -0.522940888712441 0.0120483832567209 0.342627053981254 -0.687186906466865
2.2975726,-0.618884859896728 -1.1366360750781 -0.519263746982526 -1.02470580167082 -0.522940888712441 -0.863171185425945 3.11219574032972 1.97200710658975
2.3272777,-0.651431999123483 0.55329161145762 -0.250631301876899 1.11210019001038 -0.522940888712441 -0.179808625688859 -1.04215728919298 -0.864466507337306
2.5217206,0.115499102435224 -0.512233676577595 0.286633588334355 1.13650173283446 -0.522940888712441 -0.179808625688859 0.342627053981254 -0.155348103855541
2.5533438,0.266341329949937 -0.551137885443386 -0.384947524429713 0.354857790686005 -0.522940888712441 -0.863171185425945 0.342627053981254 -0.332627704725983
2.5687881,1.16902610257751 0.855491905752846 2.03274448152093 1.22628985326088 1.89254797819741 2.02833774827712 3.11219574032972 2.68112551007152
2.6567569,-0.218972367124187 0.851192298581141 0.555266033439982 -1.02470580167082 -0.522940888712441 -0.863171185425945 0.342627053981254 0.908329501367106
2.677591,0.263121415733908 1.4142681068416 0.018001143228728 1.35980653053822 -0.522940888712441 -0.863171185425945 -1.04215728919298 -0.864466507337306
2.7180005,-0.0704736333296423 1.52000996595417 0.286633588334355 1.39364261119802 -0.522940888712441 -0.863171185425945 0.342627053981254 -0.332627704725983
2.7942279,-0.751957286017338 0.316843561689933 -1.99674219506348 0.911736065044475 -0.522940888712441 -0.863171185425945 -1.04215728919298 -0.864466507337306
2.8063861,-0.685277652430997 1.28214038482516 0.823898478545609 0.232904453212813 -0.522940888712441 -0.863171185425945 0.342627053981254 -0.155348103855541
2.8124102,-0.244991501432929 0.51882005949686 -0.384947524429713 0.823246560137838 -0.522940888712441 -0.863171185425945 0.342627053981254 0.553770299626224
2.8419982,-0.75731027755674 2.09041984898851 1.22684714620405 1.53428167116843 -0.522940888712441 -0.863171185425945 -1.04215728919298 -0.864466507337306
2.8535925,1.20962937075363 -0.242882661178889 1.09253092365124 -1.02470580167082 -0.522940888712441 1.24263233939889 3.11219574032972 2.50384590920108
2.9204698,0.570886990493502 0.58243883987948 0.555266033439982 1.16006887775962 -0.522940888712441 1.07357183940747 0.342627053981254 1.61744790484887
2.9626924,0.719758684343624 0.984970304132004 1.09253092365124 1.52137230773457 -0.522940888712441 -0.179808625688859 0.342627053981254 -0.509907305596424
2.9626924,-1.52406140158064 1.81975700990333 0.689582255992796 -1.02470580167082 -0.522940888712441 -0.863171185425945 -1.04215728919298 -0.864466507337306
2.9729753,-0.132431544081234 2.68769877553723 1.09253092365124 1.53428167116843 -0.522940888712441 -0.442797990776478 0.342627053981254 -0.687186906466865
3.0130809,0.436161292804989 -0.0834447307428255 -0.519263746982526 -1.02470580167082 1.89254797819741 1.07357183940747 0.342627053981254 1.26288870310799
3.0373539,-0.161195191984091 -0.671900359186746 1.7641120364153 1.13650173283446 -0.522940888712441 -0.863171185425945 0.342627053981254 0.0219314970149
3.2752562,1.39927182372944 0.513852869452676 0.689582255992796 -1.02470580167082 1.89254797819741 1.49394503405693 0.342627053981254 -0.155348103855541
3.3375474,1.51967002306341 -0.852203755696565 0.555266033439982 -0.104527297798983 1.89254797819741 1.85927724828569 0.342627053981254 0.908329501367106
3.3928291,0.560725834706224 1.87867703391426 1.09253092365124 1.39364261119802 -0.522940888712441 0.486423065822545 0.342627053981254 1.26288870310799
3.4355988,1.00765532502814 1.69426310090641 1.89842825896812 1.53428167116843 -0.522940888712441 -0.863171185425945 0.342627053981254 -0.509907305596424
3.4578927,1.10152996153577 -0.10927271844907 0.689582255992796 -1.02470580167082 1.89254797819741 1.97630171771485 0.342627053981254 1.61744790484887
3.5160131,0.100001934217311 -1.30380956369388 0.286633588334355 0.316555063757567 -0.522940888712441 0.28786643052924 0.342627053981254 0.553770299626224
3.5307626,0.987291634724086 -0.36279314978779 -0.922212414640967 0.232904453212813 -0.522940888712441 1.79270085261407 0.342627053981254 1.26288870310799
3.5652984,1.07158528137575 0.606453149641961 1.7641120364153 -0.432854616994416 1.89254797819741 0.528504607720369 0.342627053981254 0.199211097885341
3.5876769,0.180156323255198 0.188987436375017 -0.519263746982526 1.09956763075594 -0.522940888712441 0.708239632330506 0.342627053981254 0.199211097885341
3.6309855,1.65687973755377 -0.256675483533719 0.018001143228728 -1.02470580167082 1.89254797819741 1.79270085261407 0.342627053981254 1.26288870310799
3.6800909,0.5720085322365 0.239854450210939 -0.787896192088153 1.0605418233138 -0.522940888712441 -0.863171185425945 -1.04215728919298 -0.864466507337306
3.7123518,0.323806133438225 -0.606717660886078 -0.250631301876899 -1.02470580167082 1.89254797819741 0.342907418101747 0.342627053981254 0.199211097885341
3.9843437,1.23668206715898 2.54220539083611 0.152317365781542 -1.02470580167082 1.89254797819741 1.89037692416194 0.342627053981254 1.26288870310799
3.993603,0.180156323255198 0.154448192444669 1.62979581386249 0.576050411655607 1.89254797819741 0.708239632330506 0.342627053981254 1.79472750571931
4.029806,1.60906277046565 1.10378605019827 0.555266033439982 -1.02470580167082 -0.522940888712441 -0.863171185425945 -1.04215728919298 -0.864466507337306
4.1295508,1.0036214996026 0.113496885050331 -0.384947524429713 0.860016436332751 1.89254797819741 -0.863171185425945 0.342627053981254 -0.332627704725983
4.3851468,1.25591974271076 0.577607033774471 0.555266033439982 -1.02470580167082 1.89254797819741 1.07357183940747 0.342627053981254 1.26288870310799
4.6844434,2.09650591351268 0.625488598331018 -2.66832330782754 -1.02470580167082 1.89254797819741 1.67954222367555 0.342627053981254 0.553770299626224
5.477509,1.30028987435881 0.338383613253713 0.555266033439982 1.00481276295349 1.89254797819741 1.24263233939889 0.342627053981254 1.97200710658975

代码如下：

package vip.shuai7boy.lr

import org.apache.log4j.{Level, Logger}
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.regression.{LabeledPoint, LinearRegressionWithSGD}
import org.apache.spark.rdd.RDD
import org.apache.spark.{SparkConf, SparkContext}

object LinearRegression {

  def main(args: Array[String]) {
    // 构建Spark对象
    val conf = new SparkConf().setAppName("LinearRegressionWithSGD").setMaster("local")
    val sc = new SparkContext(conf)
    Logger.getRootLogger.setLevel(Level.WARN)

    //读取样本数据
    val data = sc.textFile("lpsa.data")
    val examples: RDD[LabeledPoint] = data.map { line =>
      val parts = line.split(',')
      val y = parts(0)
      val xs = parts(1)
      LabeledPoint(parts(0).toDouble, Vectors.dense(parts(1).split(' ').map(_.toDouble)))
    }

    val train2TestData: Array[RDD[LabeledPoint]] = examples.randomSplit(Array(0.8, 0.2), 1L)

    /*
     *  迭代次数
     *  训练一个多元线性回归模型收敛（停止迭代）条件：
     *  	1、error值小于用户指定的error值
     *  	2、达到一定的迭代次数
     */
    val numIterations = 100

    //在每次迭代的过程中 梯度下降算法的下降步长大小    0.1 0.2 0.3 0.4
    val stepSize = 0.003

    val miniBatchFraction = 1

    val lrs = new LinearRegressionWithSGD()
    //让训练出来的模型有w0参数，就是有截距
    lrs.setIntercept(true)
    //设置步长
    lrs.optimizer.setStepSize(stepSize)
    //设置迭代次数
    lrs.optimizer.setNumIterations(numIterations)
    //每一次训练完后，是否计算所有样本的误差值,1代表所有样本
    lrs.optimizer.setMiniBatchFraction(miniBatchFraction)

    val model = lrs.run(train2TestData(0))
    println("weights = " + model.weights)
    println("intercept = " + model.intercept)

    // 对样本进行测试   （下面的 features代表训练集那堆x，label代表那堆y）
    val prediction = model.predict(train2TestData(1).map(_.features))
    //将训练得到的y值和真实的y值压缩到一起
    val predictionAndLabel: RDD[(Double, Double)] = prediction.zip(train2TestData(1).map(_.label))

    val print_predict = predictionAndLabel.take(20)
    println("prediction" + "\t" + "label")
    for (i <- 0 to print_predict.length - 1) {
      println(print_predict(i)._1 + "\t" + print_predict(i)._2)
    }

    // 计算测试集平均误差
    val loss = predictionAndLabel.map {
      case (p, v) =>
        val err = p - v
        Math.abs(err)
    }.reduce(_ + _)
    val error = loss / train2TestData(1).count
    println("Test RMSE = " + error)
    // 模型保存
    //    val ModelPath = "model"
    //    model.save(sc, ModelPath)
    //    val sameModel = LinearRegressionModel.load(sc, ModelPath)
    sc.stop()
  }

}

朴素贝叶斯分类算法

什么是朴素贝叶斯？

朴素贝叶斯是基于贝叶斯定理和特征条件独立假设的分类方法。它根据已有的一些数据来进行预测，属于有监督学习算法。

公式定义：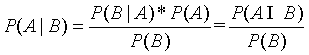

简写为：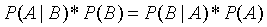

其中：

P（A）叫做A事件的先验概率，及一般情况下，认为A发生的概率。

P（B|A）叫做似然度，及假定A成立的情况下B发生的概率/

P（B）叫做标准化常量，及一般情况下，认为B发生的概率。

P（A|B）叫做后验概率。

下面举个例子来进行理解：

假设现在有一堆邮件，正常邮件的比例是80%，垃圾邮件的比例是20%，这堆邮件中，5%的邮件中出现Viagra单词，如果有一封邮件，这封邮件中包含Viagra单词，求这封邮件是垃圾邮件的概率。

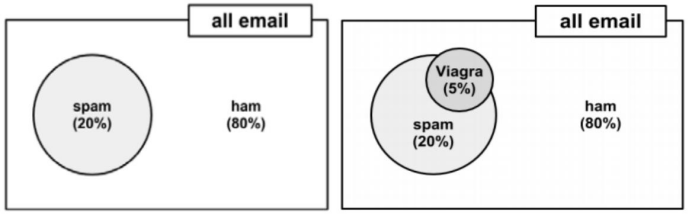
显然不能使用5%*20%=1%得到这封邮件是垃圾邮件的概率，因为出现Viagra单词的不一定是垃圾邮件，也有可能是正常邮件。那么根据贝叶斯公式可得包含Viagra单词的邮件是垃圾邮件的概率为：

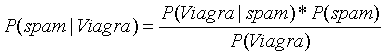
说明：

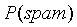是已知20%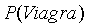，也是已知 5%，那么如果求出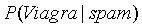的概率，结果就可以知道。我们可以根据邮件的数据集统计得到单词频率表：

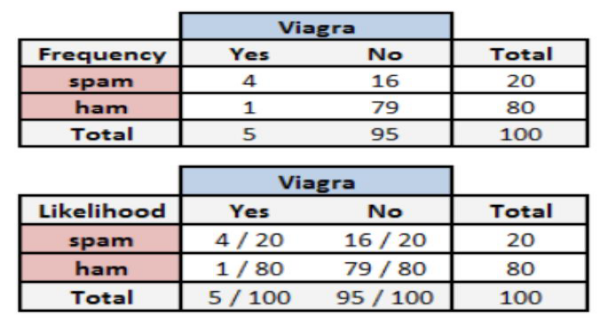
其中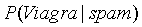表示在垃圾邮件中出现Viagra单词的概率，通过统计得出为4/20。可以得出如果一封邮件中有Viagra单词，这封邮件是垃圾邮件的概率为：

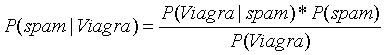
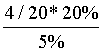​ = =0.8

通过同样的计算可以得到，含有Viagra单词但不是垃圾邮件的概率为0.2。那么可以认为这封邮件是垃圾邮件的概率比较大。这里的Viagra可以理解为邮件中的一个特征。那么当一封邮件有额外更多的特征时，贝叶斯如何扩展？

假设所有历史邮件中只出现了4个单词，也就是4个特征，根据历史邮件统计的单词频率表如下：

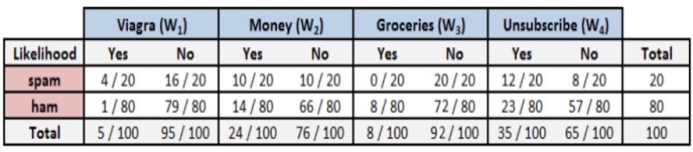
假设现在给定一封邮件中有Viagra和Unsubscribe(取消订阅)两个单词，求这封邮件 是垃圾邮件的概率、不是垃圾邮件的概率？

利用贝叶斯公式，我们可以得到：

是垃圾邮件的概率：

=

=

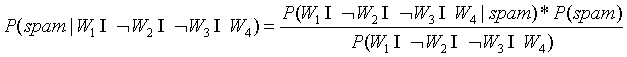
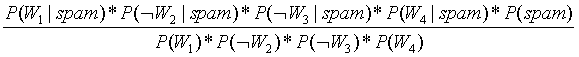
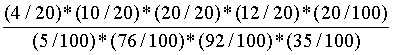
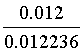
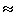= 98.07%

不是垃圾邮件的概率：

=

=

=

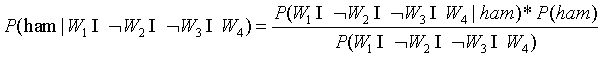
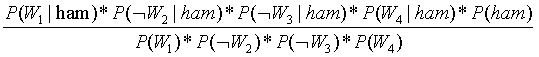
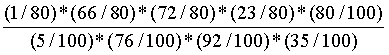
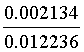
=17.4%

拉普拉斯估计

根据以上例子，假设有一封邮件这4个单词都出现了，求这封邮件是垃圾邮件的概率：

=

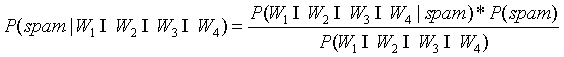
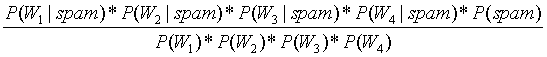
由于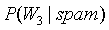的概率为0/20，会导致整个结果是垃圾邮件的概率为0，那么就否定了其它单词出现的权重。

拉普拉斯估计本质上是给频率表中的每个单词的计数加上一个较小的数，这样就保证每一类中每个特征发生的概率非零。通常，拉普拉斯估计中加上的数值为1，这样就保证了每一个特征至少在数据中出现一次。

以上例子如果四个单词都出现情况下计算是否是垃圾邮件，出现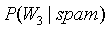的概率为0/20，可以增加4封垃圾邮件，使4封邮件中每个邮件中只有一个单词出现，这样就避免了垃圾邮件中有的单词出现概率为0的情况。同样在不是垃圾邮件中也增加4封，避免在正常邮件中出现有的单词出现概率为0的情况。

Python贝叶斯案例

训练数据集（这里仅仅列出了一部分，可以按照此格式自行扩展）：

type,text
ham,you are having a good week. Just checking in
ham,K..give back my thanks.
ham,Am also doing in cbe only. But have to pay.
spam,"complimentary 4 STAR Ibiza Holiday or £10,000 cash needs your URGENT collection. 09066364349 NOW from Landline not to lose out! Box434SK38WP150PPM18+"
spam,okmail: Dear Dave this is your final notice to collect your 4* Tenerife Holiday or #5000 CASH award! Call 09061743806 from landline. TCs SAE Box326 CW25WX 150ppm
ham,Aiya we discuss later lar... Pick u up at 4 is it?
ham,Are you this much buzytype,text
ham,you are having a good week. Just checking in
ham,K..give back my thanks.
ham,Am also doing in cbe only. But have to pay.
spam,"complimentary 4 STAR Ibiza Holiday or £10,000 cash needs your URGENT collection. 09066364349 NOW from Landline not to lose out! Box434SK38WP150PPM18+"
spam,okmail: Dear Dave this is your final notice to collect your 4* Tenerife Holiday or #5000 CASH award! Call 09061743806 from landline. TCs SAE Box326 CW25WX 150ppm
ham,Aiya we discuss later lar... Pick u up at 4 is it?
ham,Are you this much buzy

代码如下：

# coding:utf-8
import os
import sys
# codecs 编码转换模块
import codecs
from sklearn.naive_bayes import MultinomialNB
from sklearn.feature_extraction.text import CountVectorizer

if __name__ == '__main__':
    # 读取文本构建语料库
    corpus = []
    labels = []
    corpus_test = []
    labels_test = []
    f = codecs.open("./sms_spam.txt", "rb")
    count = 0
    while True:
        # readline() 方法用于从文件读取整行，包括 "\n" 字符。
        line = f.readline().decode("utf-8")
        # 读取第一行，第一行数据是列头，不统计
        if count == 0:
            count = count + 1
            continue
        if line:
            count = count + 1
            line = line.split(",")
            label = line[0]
            sentence = line[1]
            corpus.append(sentence)
            if "ham" == label:
                labels.append(0)
            elif "spam" == label:
                labels.append(1)
            if count > 5550:
                corpus_test.append(sentence)
                if "ham" == label:
                    labels_test.append(0)
                elif "spam" == label:
                    labels_test.append(1)
        else:
            break
    # 文本特征提取：
    #     将文本数据转化成特征向量的过程
    #     比较常用的文本特征表示法为词袋法
    #
    # 词袋法：
    #     不考虑词语出现的顺序，每个出现过的词汇单独作为一列特征
    #     这些不重复的特征词汇集合为词表
    #     每一个文本都可以在很长的词表上统计出一个很多列的特征向量
    # CountVectorizer是将文本向量转换成稀疏表示数值向量（字符频率向量）  vectorizer 将文档词块化,只考虑词汇在文本中出现的频率
    # 词袋 (将文本向量化)
    vectorizer = CountVectorizer()
    # 每行的词向量，fea_train是一个矩阵
    fea_train = vectorizer.fit_transform(corpus)

    print("vectorizer.get_feature_names is ", vectorizer.get_feature_names())
    print("fea_train is ", fea_train.toarray())

    # vocabulary=vectorizer.vocabulary_ 只计算上面vectorizer中单词的tf(term frequency 词频)
    vectorizer2 = CountVectorizer(vocabulary=vectorizer.vocabulary_)
    fea_test = vectorizer2.fit_transform(corpus_test)
    
    # alpha = 1 拉普拉斯估计给每个单词个数加1
    clf = MultinomialNB(alpha=1)
    clf.fit(fea_train, labels)

    pred = clf.predict(fea_test);
    # 根据概率推测正常和垃圾
    for p in pred:
        if p == 0:
            print("正常邮件")
        else:
            print("垃圾邮件")

KNN算法

什么是KNN算法？

KNN全称k-Nearest Neighbor。它是把一个点种类归属为周边点数最多的那个类。

举个例子：

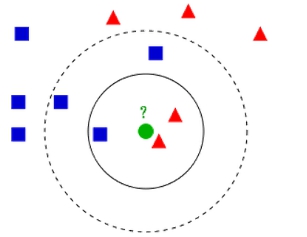
如果K = 3，绿色圆点的最近的3个邻居是2个红色小三角形和1个蓝色小正方形，少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于红色的三角形一类。

如果K = 5，绿色圆点的最近的5个邻居是2个红色三角形和3个蓝色的正方形，还是少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于蓝色的正方形一类。

这里涉及三个元素：K值，距离计算还有决策分类

K值一般选取小于样本数据的平方根，一般是不大于20的整数。

距离就是计算余弦值。

决策分类就是少数服从多数。

KNN算法步骤

1）.计算所有元素和选定点的距离

2）.根据距离进行排序

3）.选择离点最近的K个点

4）.求出前K个点所在类别的概率

5）.返回概率最大的最为当前点预测分类

KNN算法复杂度

计算的时间复杂度和样本数据呈正比，当样本数据为n时，时间复杂度是o(n)。

KNN数据归一化

比如训练的数据中含有不同维度时，比如每天工作时间0-24，每天心跳次数0-20000，这样心跳次数这个权重（维度）明显很大，而工作时间权重（维度）却很小，这样结果就很容易受权重影响。有时候我们需要忽略权重带来的影响，所以进行机器训练时，最好先进行归一化，将数据映射到[0,1]区间上。

归一化公式：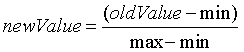

距离度量

欧式距离：因为距离肯定是大于0的，所以一般都是坐标相减，平方后再开方。

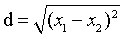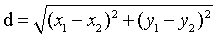距离公式：一维： 二维： 三维：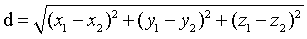

KNN案例

训练数据集（这里仅仅列出了一部分，可以按照此格式自行扩展）：

飞行距离，玩游戏时间，看书时长，魅力值

40920	8.326976	0.953952	3

14488	7.153469	1.673904	2

26052	1.441871	0.805124	1

75136	13.147394	0.428964	1

38344	1.669788	0.134296	1

72993	10.141740	1.032955	1

35948	6.830792	1.213192	3

42666	13.276369	0.543880	3

67497	8.631577	0.749278	1

35483	12.273169	1.508053	3

代码如下：

# coding:utf-8

import numpy as np
import operator
# matplotlib 绘图模块
import matplotlib.pyplot as plt

'''
根据出行距离，上网时长，看书时长三个维度测量某人的魅力值
'''

# normData 测试数据集的某行，  dataSet 训练数据集 ，labels 训练数据集的类别，k k的值
def classify(normData, dataSet, labels, k):
    # 计算行数 []填0是计算行，填1是计算列
    dataSetSize = dataSet.shape[0]
    # 当前点到所有点的坐标差值  ,np.tile(x,(y,1)) 复制x 共y行 1列
    diffMat = np.tile(normData, (dataSetSize, 1)) - dataSet
    # 对每个坐标差值平方
    sqDiffMat = diffMat ** 2
    # 对于二维数组 sqDiffMat.sum(axis=0)指 对向量每列求和，sqDiffMat.sum(axis=1)是对向量每行求和,返回一个长度为行数的数组
    # 例如：narr = array([[ 1.,  4.,  6.],
    #                   [ 2.,  5.,  3.]])
    #    narr.sum(axis=1) = array([ 11.,  10.])
    #    narr.sum(axis=0) = array([ 3.,  9.,  9.])
    sqDistances = sqDiffMat.sum(axis=1)
    # 欧式距离 最后开方
    distance = sqDistances ** 0.5
    # x.argsort() 将x中的元素从小到大排序，提取其对应的index 索引，返回数组
    # 例：   tsum = array([ 11.,  10.])    ----  tsum.argsort() = array([1, 0])
    sortedDistIndicies = distance.argsort()
    #     classCount保存的K是魅力类型   V:在K个近邻中某一个类型的次数
    classCount = {}
    for i in range(k):
        # 获取对应的下标的类别
        voteLabel = labels[sortedDistIndicies[i]]
        # 给相同的类别次数计数
        classCount[voteLabel] = classCount.get(voteLabel, 0) + 1
    # sorted 排序 返回新的list
    #     sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
    sortedClassCount = sorted(classCount.items(), key=lambda x: x[1], reverse=True)
    return sortedClassCount[0][0]


def file2matrix(filename):
    fr = open(filename, "rb")
    # readlines:是一次性将这个文本的内容全部加载到内存中(列表)
    arrayOflines = fr.readlines()
    numOfLines = len(arrayOflines)
    #     print "numOfLines = " , numOfLines
    # numpy.zeros 创建给定类型的数组  numOfLines 行 ，3列
    returnMat = np.zeros((numOfLines, 3))
    # 存结果的列表
    classLabelVector = []
    index = 0
    for line in arrayOflines:
        # 去掉一行的头尾空格
        line = line.decode("utf-8").strip()
        listFromline = line.split('\t')
        returnMat[index, :] = listFromline[0:3]
        classLabelVector.append(int(listFromline[-1]))
        index += 1
    return returnMat, classLabelVector


'''
    将训练集中的数据进行归一化
    归一化的目的：
        训练集中飞行公里数这一维度中的值是非常大，那么这个纬度值对于最终的计算结果(两点的距离)影响是非常大，
        远远超过其他的两个维度对于最终结果的影响
    实际约会姑娘认为这三个特征是同等重要的
    下面使用最大最小值归一化的方式将训练集中的数据进行归一化
'''


# 将数据归一化
def autoNorm(dataSet):
    #     dataSet.min(0)   代表的是统计这个矩阵中每一列的最小值     返回值是一个矩阵1*3矩阵
    # 例如： numpyarray = array([[1,4,6],
    #                        [2,5,3]])
    #    numpyarray.min(0) = array([1,4,3])    numpyarray.min(1) = array([1,2])
    #    numpyarray.max(0) = array([2,5,6])    numpyarray.max(1) = array([6,5])
    minVals = dataSet.min(0)
    maxVals = dataSet.max(0)
    ranges = maxVals - minVals
    # dataSet.shape[0] 计算行数， shape[1] 计算列数
    m = dataSet.shape[0]

    #     print '行数 = %d' %(m)
    #     print maxVals

    #     normDataSet存储归一化后的数据
    #     normDataSet = np.zeros(np.shape(dataSet))
    # np.tile(minVals,(m,1)) 在行的方向上重复 minVals m次 即复制m行，在列的方向上重复munVals 1次，即复制1列
    normDataSet = dataSet - np.tile(minVals, (m, 1))
    normDataSet = normDataSet / np.tile(ranges, (m, 1))
    return normDataSet, ranges, minVals


def datingClassTest():
    rate = 0.1
    datingDataMat, datingLabels = file2matrix('./datingTestSet.txt')
    # 将数据归一化
    normMat, ranges, minVals = autoNorm(datingDataMat)
    # m 是 ： normMat行数 = 1000
    m = normMat.shape[0]
    #     print 'm =%d 行'%m
    # 取出100行数据测试
    numTestVecs = int(m * rate)
    errorCount = 0.0
    for i in range(numTestVecs):
        # normMat[i,:] 取出数据的第i行,normMat[numTestVecs:m,:]取出数据中的100行到1000行 作为训练集，
        # datingLabels[numTestVecs:m] 取出数据中100行到1000行的类别，4是K
        classifierResult = classify(normMat[i, :], normMat[numTestVecs:m, :], datingLabels[numTestVecs:m], 4)
        print('模型预测值: %d ,真实值 : %d' % (classifierResult, datingLabels[i]))
        if (classifierResult != datingLabels[i]):
            errorCount += 1.0
    errorRate = errorCount / float(numTestVecs)
    print('正确率 : %f' % (1 - errorRate))
    return 1 - errorRate


'''
    拿到每条样本的飞行里程数和玩视频游戏所消耗的时间百分比这两个维度的值，使用散点图
'''


def createScatterDiagram():
    datingDataMat, datingLabels = file2matrix('datingTestSet.txt')
    type1_x = []
    type1_y = []
    type2_x = []
    type2_y = []
    type3_x = []
    type3_y = []
    # 生成一个新的图像
    fig = plt.figure()
    # matplotlib下, 一个 Figure 对象可以包含多个子图(Axes), 可以使用 subplot() 快速绘制
    # subplot(numRows, numCols, plotNum)图表的整个绘图区域被分成 numRows 行和 numCols 列,按照从左到右，从上到下的顺序对每个子区域进行编号，左上的子区域的编号为1
    # plt.subplot(111)等价于plt.subplot(1,1,1)
    axes = plt.subplot(111)
    # 设置字体 黑体  ，用来正常显示中文标签
    plt.rcParams['font.sans-serif'] = ['SimHei']

    for i in range(len(datingLabels)):
        if datingLabels[i] == 1:  # 不喜欢
            type1_x.append(datingDataMat[i][0])
            type1_y.append(datingDataMat[i][1])

        if datingLabels[i] == 2:  # 魅力一般
            type2_x.append(datingDataMat[i][0])
            type2_y.append(datingDataMat[i][1])

        if datingLabels[i] == 3:  # 极具魅力
            type3_x.append(datingDataMat[i][0])
            type3_y.append(datingDataMat[i][1])

    # 绘制散点图 ，前两个参数表示相同长度的数组序列 ，s 表示点的大小， c表示颜色
    type1 = axes.scatter(type1_x, type1_y, s=20, c='red')
    type2 = axes.scatter(type2_x, type2_y, s=40, c='green')
    type3 = axes.scatter(type3_x, type3_y, s=50, c='blue')
    plt.title(u'标题')
    plt.xlabel(u'每年飞行里程数')
    plt.ylabel(u'玩视频游戏所消耗的时间百分比')
    # loc 设置图例的位置 2是upper left
    axes.legend((type1, type2, type3), (u'不喜欢', u'魅力一般', u'极具魅力'), loc=2)
    #     plt.scatter(datingDataMat[:,0],datingDataMat[:,1],c = datingLabels)
    plt.show()


def classifyperson():
    resultList = ['没感觉', '看起来还行', '极具魅力']
    # input_man = [20000, 3, 2]
    input_man = [70808, 9.778763, 1.084103]
    datingDataMat, datingLabels = file2matrix('datingTestSet.txt')
    normMat, ranges, minVals = autoNorm(datingDataMat)
    result = classify((input_man - minVals) / ranges, normMat, datingLabels, 5)
    print('你即将约会的人是:%s' % resultList[result - 1])


if __name__ == '__main__':
    # createScatterDiagram()  # 观察数据的分布情况
    acc = datingClassTest()
    if (acc > 0.9):
        classifyperson()

K-means算法

什么是K-menas？

K-means属于无监督学习，它是根据距离聚类的算法。

K-means算法流程

1）.首先选取K个点作为类别的中心点。

2）.计算每个元素到所有中心点的距离，将距离最近的点作为归属类。

3）.重新选取K个点进行迭代

4）.重复2，3步骤，直到K个中心点位置不变的时候停止迭代或者达到预期设定值停止迭代。

什么是K-means++？

K-Means++是对K-Means的一种改进。我们在选取中心点的时候，如果中心点距离太近，就会增加迭代次数，所以最好分散，K-Means++就解决了这种选取中心点的问题，它第一次选择中心点是随机的，后面则选择距离已选择的中心点较远的点作为新的中心点，这样大大降低了迭代次数。

K-means案例

统计每个坐标所属分类：

训练数据集（这里仅仅列出了一部分，可以按照此格式自行扩展）：

1.658985	4.285136

-3.453687	3.424321

4.838138	-1.151539

-5.379713	-3.362104

0.972564	2.924086

-3.567919	1.531611

0.450614	-3.302219

代码：

# encoding:utf-8

import numpy as np


# 将每行数据放入一个数组内列表，返回一个二维列表

def loadDataSet(fileName):
    # 创建空列表
    dataMat = []
    fr = open(fileName, "rb")
    for line in fr.readlines():
        # 按照制表符切割每行，返回一个列表list
        curLine = line.decode("utf-8").strip().split('\t')
        # 将切分后的每个列表中的元素，以float形式返回，map()内置函数，返回一个map object【注意，在python2.7版本中map直接返回list】，这里需要再包装个list
        fltLine = list(map(float, curLine))
        dataMat.append(fltLine)
    return dataMat


# 两点欧式距离
def distEclud(vecA, vecB):
    # np.power(x1,x2)  对x1中的每个元素求x2次方,不会改变x1。
    return np.sqrt(np.sum(np.power(vecA - vecB, 2)))


# 随机找到3个中心点的位置坐标，返回一个3*2的矩阵
def randCent(dataSet, k):
    # 返回dataSet列数,2列
    n = np.shape(dataSet)[1]
    '''
        centerids是一个3*2的矩阵，用于存储三个中心点的坐标
    '''
    centerids = np.mat(np.zeros((k, n)))
    for j in range(n):
        # 统计每一列的最小值
        minJ = min(dataSet[:, j])
        # 每列最大值与最小值的差值
        rangeJ = float(max(dataSet[:, j]) - minJ)
        # np.random.rand(k,1) 产生k行1列的数组，里面的数据是0~1的浮点型 随机数。
        array2 = minJ + rangeJ * np.random.rand(k, 1)
        # 转换成k*1矩阵 赋值给centerids
        centerids[:, j] = np.mat(array2)
    return centerids


def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):
    # 计算矩阵所有 行数  m=80
    m = np.shape(dataSet)[0]
    # zeros((m,2)) 创建一个80行，2列的二维数组
    # numpy.mat 将二维数组转换成矩阵  【类别号，当前点到类别号中心点的距离】
    clusterAssment = np.mat(np.zeros((m, 2)))
    # createCent找到K个随机中心点坐标
    centerids = createCent(dataSet, k)
    #     print centerids
    clusterChanged = True
    while clusterChanged:
        clusterChanged = False
        # 遍历80个数据到每个中心点的距离
        for i in range(m):
            # np.inf float的最大值，无穷大
            minDist = np.inf
            # 当前点属于的类别号
            minIndex = -1
            # 每个样本点到三个中心点的距离
            for j in range(k):
                # x = centerids[j,:]
                # print x
                # 返回两点距离的值
                distJI = distMeas(centerids[j, :], dataSet[i, :])
                if distJI < minDist:
                    # 当前最小距离的值
                    minDist = distJI
                    # 当前最小值属于哪个聚类
                    minIndex = j
            # 有与上次迭代计算的当前点的类别不相同的点
            if clusterAssment[i, 0] != minIndex:
                clusterChanged = True
            # 将当前点的类别号和最小距离 赋值给clusterAssment的一行
            clusterAssment[i, :] = minIndex, minDist
        for cent in range(k):
            # array = clusterAssment[:,0].A==cent
            # result = np.nonzero(clusterAssment[:,0].A==cent)[0]
            # clusterAssment[:,0].A 将0列 也就是类别号转换成数组
            # clusterAssment[:,0].A==cent 返回的是一列，列中各个元素是 True或者False,True代表的是当前遍历的cent类别
            # np.nonzero(clusterAssment[:,0].A==cent)  返回数组中值不为False的元素对应的行号下标数组 和列号下标数组
            # currNewCenter 取出的是对应是当前遍历cent类别的 所有行数据组成的一个矩阵
            currNewCenter = dataSet[np.nonzero(clusterAssment[:, 0].A == cent)[0]]
            # numpy.mean 计算矩阵的均值，axis=0计算每列的均值，axis=1计算每行的均值。
            # 这里是每经过一次while计算都会重新找到各个类别中中心点坐标的位置  ，axis = 0 是各个列求均值
            centerids[cent, :] = np.mean(currNewCenter, axis=0)
            # 返回 【 当前三个中心点的坐标】 【每个点的类别号，和到当前中心点的最小距离】
    return centerids, clusterAssment


if __name__ == '__main__':
    # numpy.mat 将数据转换成80*2的矩阵
    # testSet.txt文件每一行是一个坐标
    dataMat = np.mat(loadDataSet('./testSet.txt'))
    k = 3
    # centerids 三个中心点的坐标。clusterAssment 每个点的类别号|到当前中心点的最小距离
    centerids, clusterAssment = kMeans(dataMat, k, distMeas=distEclud, createCent=randCent)
    print(centerids)
    print(clusterAssment)

TF-IDF算法

TF-IDF是什么？

IT-IDF是求在一篇文章中某些单词出现的频率最高，但是在整个资料库中却出现很少的词汇。

TF公式：

IDF公式：

PS：+1的意思是防止分母出现0

TF-IDF公式：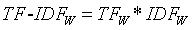

Scala微博分类案例

总结多个微博的大致类别

（这里仅仅列出了一部分，可以按照此格式自行扩展）：

3792144327929371	#谢谢你陪我走过2014#2014，首先我要感谢我的妈妈和外婆，是你们一直在辛苦的帮我照顾着宝宝，再来要感谢我的宝宝，你的出生给我们带来了很多的欢乐，看着你一天天健康快乐的成长是我这生最大的幸福，最后我想对你们说一声：谢谢！希望妈妈受伤的脚能好起来，希望在新的一年里越来越好@錵池雨姗 @九阳
3792144370354258	#谢谢你陪我走过2014#大脚和小脚，一起走天涯，祝我的小妞永远幸福！2015年继续带你走中国！[心] @茶小妹儿de爱 快来接棒，支持小阳好活动！@九阳
3792144483136367	#谢谢你陪我走过2014# 老公，2014，我们一起同在，2014,我们一起同病魔抗衡；2014,我们一起携手走过。相识的１４年里，你关心我，温暖我，无论喜怒哀乐，我都愿与你一同分享；一年四季，365天，我们一生一世，不离不弃，爱的丘比特之箭将你我牢牢的串在了一起，爱你，祝你健康@桐桐宝宝爱妈咪 @九阳
3792144521609547	我谢谢我的姐姐！老公上夜班她每晚陪我入睡！谢谢你陪我逛街陪我入睡！陪我走过2014@九阳 @肉嘟嘟叫妈妈 争取九阳足浴桶送姐姐
3792144852499797	 @九阳 九阳小编看过来[爱你]
3792144978705987	#谢谢你陪我走过2014#2014，感谢陪伴！辛苦一年了，泡泡脚@动物园里快乐多 @九阳
3792145045458545	#谢谢你陪我走过2014#看到九阳的活动真的是好激动，因为我家就需要一个洗脚桶呢。为什么呢？因为我家宝贝每天会给我洗脚，说我辛苦，小小的人儿每天端着不像样的小桶，我的心也酸酸的，希望九阳能给我家宝宝减轻负担，送个桶把，2014年你送桶了吗？@九阳 @我们家有2宝贝
3792145066207002	发表了博文《我正在看搞笑微电影九阳真精，简直是太搞笑了，分享给大家！》我正在看搞笑微电影九阳真精，简直是太搞笑了，分享给大家！http://t.cn/RZ7AUUu

代码:

package shuai7boy.vip.kmeans

import scala.collection.mutable.ArrayBuffer
import scala.collection.mutable.ListBuffer

import org.apache.lucene.analysis.TokenStream
import org.apache.lucene.analysis.tokenattributes.CharTermAttribute
import org.apache.spark.SparkConf
import org.apache.spark.SparkContext
import org.apache.spark.mllib.clustering.KMeans
import org.apache.spark.mllib.feature.HashingTF
import org.apache.spark.mllib.feature.IDF
import org.apache.spark.mllib.feature.IDFModel
import org.apache.spark.rdd.RDD
import org.wltea.analyzer.lucene.IKAnalyzer
import org.apache.spark.mllib.linalg.Vector
import org.apache.spark.mllib.clustering.KMeansModel

object BlogKMeans {

  def main(args: Array[String]) {
    val conf = new SparkConf().setAppName("BlogKMeans").setMaster("local[*]")
    val sc = new SparkContext(conf)

    val rdd = sc.textFile("./original.txt", 100)
    var wordRDD: RDD[(String, ArrayBuffer[String])] = rdd.mapPartitions(iterator => {
      val list = new ListBuffer[(String, ArrayBuffer[String])]
      while (iterator.hasNext) {
        //创建分词对象   IKAnalyzer支持两种分词模式：最细粒度和智能分词模式，如果构造函数参数为false，那么使用最细粒度分词。
        val analyzer = new IKAnalyzer(true)
        val line = iterator.next()
        val textArr = line.split("\t")
        val id = textArr(0)
        val text = textArr(1)
        //分词     第一个参数只是标识性，没有实际作用，第二个读取的数据
        val ts: TokenStream = analyzer.tokenStream("", text)
        //得到相应词汇的内容
        val term: CharTermAttribute = ts.getAttribute(classOf[CharTermAttribute])
        //重置分词器，使得tokenstream可以重新返回各个分词
        ts.reset()
        val arr = new ArrayBuffer[String]
        //遍历分词数据
        while (ts.incrementToken()) {
          arr.+=(term.toString())
        }

        list.append((id, arr))
        analyzer.close()
      }
      list.iterator
    })

    /**
     * wordRDD 是一个KV格式的RDD
     * K:微博ID
     * V:微博内容分词后的结果 ArrayBuffer
     */
    wordRDD = wordRDD.cache()
    //    val allDicCount = wordRDD.flatMap(one=>{one._2}).distinct().count()
    /**
     * HashingTF 使用hash表来存储分词
     * HashingTF 是一个Transformer 转换器，在文本处理中，接收词条的集合然后把这些集合转化成固定长度的特征向量,这个算法在哈希的同时会统计各个词条的词频
     * 提高hash表的桶数，默认特征维度是 2的20次方 = 1,048,576
     * 1000:只是计算每篇微博中1000个单词的词频
     */
    val hashingTF: HashingTF = new HashingTF(1000)

    val tfRDD: RDD[(String, Vector)] = wordRDD.map(x => {
      (x._1, hashingTF.transform(x._2))
    })

    /**
     * tfRDD
     * K:微博ID
     * V:Vector（tf，tf，tf.....）
     *
     * hashingTF.transform(x._2)
     * 按照hashingTF规则 计算分词频数（TF）
     */
    //    tfRDD.foreach(println)

    /**
     * 得到IDFModel，要计算每个单词在整个语料库中的IDF
     * IDF是一个 Estimator 评价器，在一个数据集上应用它的fit（）方法，产生一个IDFModel。 该IDFModel 接收特征向量（由HashingTF产生）
     * new IDF().fit(tfRDD.map(_._2)) 就是在组织训练这个评价器，让评价器知道语料库中有那些个词块，方便计算IDF
     */
    val idf: IDFModel = new IDF().fit(tfRDD.map(_._2))

    /**
     * K:微博 ID
     * V:每一个单词的TF-IDF值
     * tfIdfs这个RDD中的Vector就是训练模型的训练集
     * 计算TFIDF值
     */

    val tfIdfs: RDD[(String, Vector)] = tfRDD.mapValues(idf.transform(_))
    //    tfIdfs.foreach(println)

    /**
     * 如何知道tfIdfs 中Vector中的每个词对应的分词？？？
     *
     * wordRDD [微博ID,切出的来的单词数组]
     *
     * hashingTF.indexOf(item)  方法传入一个单词item，返回当前词组item 在hashingTF转换器写对应的分区号
     * 以下的做法就是按照每个词由hashingTF 映射的分区号由小到大排序，得到的每个词组对应以上得到的tfIdfs 值的顺序
     */
    wordRDD = wordRDD.mapValues(buffer => {
      buffer.distinct.sortBy(item => {
        hashingTF.indexOf(item)
      })
    })


    //设置聚类个数
    val kcluster = 20
    val kmeans = new KMeans()
    kmeans.setK(kcluster)
    //使用的是kemans++算法来训练模型  "random"|"k-means||"
    kmeans.setInitializationMode("k-means||")
    //设置最大迭代次数
    kmeans.setMaxIterations(1000)
    //训练模型
    val kmeansModel: KMeansModel = kmeans.run(tfIdfs.map(_._2))
    //    kmeansModel.save(sc, "d:/model001")
    //打印模型的20个中心点
    println(kmeansModel.clusterCenters)

    /**
     * 模型预测
     */
    val modelBroadcast = sc.broadcast(kmeansModel)
    /**
     * predicetionRDD KV格式的RDD
     * K：微博ID
     * V：分类号
     */
    val predicetionRDD: RDD[(String, Int)] = tfIdfs.mapValues(vetor => {
      val model = modelBroadcast.value
      model.predict(vetor)
    })
    /**
     * 总结预测结果
     * tfIdfs2wordsRDD:kv格式的RDD
     * K：微博ID
     * V：二元组(Vector(tfidf1,tfidf2....),ArrayBuffer(word,word,word....))
     */
    val tfIdfs2wordsRDD: RDD[(String, (Vector, ArrayBuffer[String]))] = tfIdfs.join(wordRDD)

    /**
     * result:KV
     * K：微博ID
     * V:(类别号，(Vector(tfidf1,tfidf2....),ArrayBuffer(word,word,word....)))
     */
    val result: RDD[(String, (Int, (Vector, ArrayBuffer[String])))] =
      predicetionRDD.join(tfIdfs2wordsRDD)

    /**
     * 查看1号类别中tf-idf比较高的单词，能代表这类的主题
     */
    result
      .filter(x => x._2._1 == 1)
      .flatMap(line => {

        val tfIdfV: Vector = line._2._2._1
        val words: ArrayBuffer[String] = line._2._2._2
        val list = new ListBuffer[(Double, String)]

        for (i <- 0 until words.length) {
          //hashingTF.indexOf(words(i)) 当前单词在1000个向量中的位置
          list.append((tfIdfV(hashingTF.indexOf(words(i))), words(i)))
        }
        list
      })
      .sortBy(x => x._1, false)
      .map(_._2).distinct()
      .take(30).foreach(println)


    sc.stop()
  }
}

// stopword.dic用于调节不统计哪些词,ext.dic用于调节统计哪些词

逻辑回归

什么是逻辑回归？

逻辑回归也属于线性回归，不过它是广义的线性回归。线性回归要求的是连续的线性变量，逻辑回归要求的结果是分类的，输出的类别概率都在0~1之间。

那么什么时候用线性回归，什么时候用逻辑回归？

比如要分析年龄，身高，体重之间的影响，如果体重仅仅要求是实际重量，那么就用线性回归。如果要把重量进行分类，比如高，中，低，那么就用逻辑回归。

逻辑回归公式：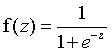

e代表自然对数，它是无限不循环小数：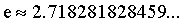

e=w₀+w₁x₁+w₂x₂+w₃*x₃+...

逻辑回归又叫逻辑函数，它是S型函数，图像如下所示：

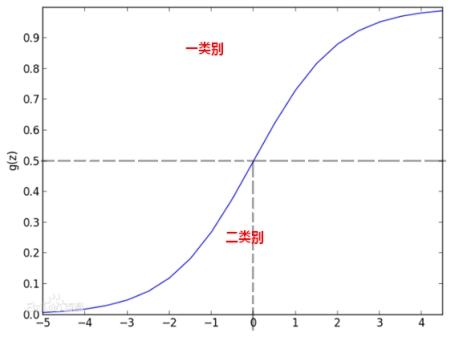
可以看到它是以0.5为界限，并且区间分布在0~1之间。当z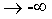时，f(z)趋近于0。当z=0时，f(z)=0.5。

Python音乐分类案例

主要思想就是将文件内容进行傅里叶转换，然后每个文件提取1000个特征进行训练。

训练完后的模型可以保存。最好就可以抽取一首音乐进行验证，它会根据特征找出最相似的音乐类别进行返回。

训练数据集：

多个音乐文件

代码：

# coding:utf-8

from scipy import fft
from scipy.io import wavfile
from sklearn.linear_model import LogisticRegression

import numpy as np

"""
使用logistic regression处理音乐数据,音乐数据训练样本的获得和使用快速傅里叶变换（FFT）预处理的方法需要事先准备好
1. 把训练集扩大到每类100个首歌,类别仍然是六类:jazz,classical,country, pop, rock, metal
2. 同时使用logistic回归训练模型
3. 引入一些评价的标准来比较Logistic测试集上的表现 
"""


# 准备音乐数据
# def create_fft(g, n):
#     rad = "i:/genres/" + g + "/converted/" + g + "." + str(n).zfill(5) + ".au.wav"
#     # sample_rate 音频的采样率，X代表读取文件的所有信息
#     (sample_rate, X) = wavfile.read(rad)
#     # 取1000个频率特征  也就是振幅
#     fft_features = abs(fft(X)[:1000])
#     # zfill(5) 字符串不足5位，前面补0
#     save = "i:/trainset/" + g + "." + str(n).zfill(5) + ".fft"
#     np.save(save, fft_features)


# -------create fft 构建训练集--------------

# genre_list = ["classical", "jazz", "country", "pop", "rock", "metal", "hiphop"]
# for g in genre_list:
#     for n in range(100):
#         create_fft(g, n)
#         print('running...')
# print('all is finished')

# =========================================================================================
# 加载训练集数据,分割训练集以及测试集,进行分类器的训练
# 构造训练集！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！
# -------read fft--------------
genre_list = ["classical", "jazz", "country", "pop", "rock", "metal", "hiphop"]
X = []
Y = []
for g in genre_list:
    for n in range(100):
        rad = "i:/trainset/" + g + "." + str(n).zfill(5) + ".fft" + ".npy"
        # 加载文件
        fft_features = np.load(rad)
        X.append(fft_features)
        # genre_list.index(g) 返回匹配上类别的索引号
        Y.append(genre_list.index(g))

# 构建的训练集
X = np.array(X)
# 构建的训练集对应的类别
Y = np.array(Y)

# 接下来，我们使用sklearn，来构造和训练我们的两种分类器 
# ------train logistic classifier--------------
model = LogisticRegression()
# 需要numpy.array类型参数
model.fit(X, Y)

print('Starting read wavfile...')
# prepare test data-------------------
sample_rate, test = wavfile.read("i:/heibao-wudizirong-remix.wav")
print(sample_rate, test, len(test))
testdata_fft_features = abs(fft(test))[:1000]
# model.predict(testdata_fft_features) 预测为一个数组，array([类别])
type_index = model.predict([testdata_fft_features])

print(type_index, type(type_index))
print(genre_list[type_index[0]])

逻辑回归优化

有无截距

对于逻辑回归分类，就是找到z那条直线，不通过原点有截距的直线与通过原点的直线相比，有截距更能将数据分类的彻底。

线性不可分问题

对于线性不可分问题，可以使用升高维度的方式转换成线性可分问题。低维空间的非线性问题在高维空间往往会成为线性问题。

调整分类阈值

在一些特定的场景下，如果按照逻辑回归默认的分类阈值0.5来进行分类的话，可能存在一些潜在的风险，比如，假如使用逻辑回归预测一个病人得癌症的概率是0.49，那么按照0.5的阈值，病人推测出来是没有得癌症的，但是49%的概率得癌症，比例相对来说得癌症的可能性也是很高，那么我们就可以降低分类的阈值，比如将阈值设置为0.3，小于0.3认为不得癌症，大于0.3认为得癌症，这样如果病人真的是癌症患者，规避掉了0.49概率下推断病人是不是癌症的风险。

鲁棒性调优

鲁棒是Robust的音译，也就是健壮和强壮的意思,比如说，计算机软件在输入错误、磁盘故障、网络过载或有意攻击情况下，能不死机、不崩溃，就是该软件的鲁棒性，那么算法的鲁棒性就是指这个算法的抗干扰能力强。

归一化数据

归一化数据可以使各个特征维度对目标函数的影响权重一致，提高迭代的求解的收敛速度。

调整数据的正负值-均值归一化

均值归一化是将原来的特征值减去这个特征在数据集中的均值，这样就会使x的各个维度取值上有正有负，在迭代求⊙参数时，能减少迭代的次数。

训练方法选择

训练逻辑回归的方法有：SGD和L-BFGS，两者区别为：

SGD:随机从训练集选取数据训练，不归一化数据，需要专门在外面进行归一化，支持L1,L2正则化，不支持多分类。

L-BFGS:所有的数据都会参与训练，算法融入方差归一化和均值归一化。支持L1,L2正则化，支持多分类。

模型评估ROC，AUC

混淆矩阵：

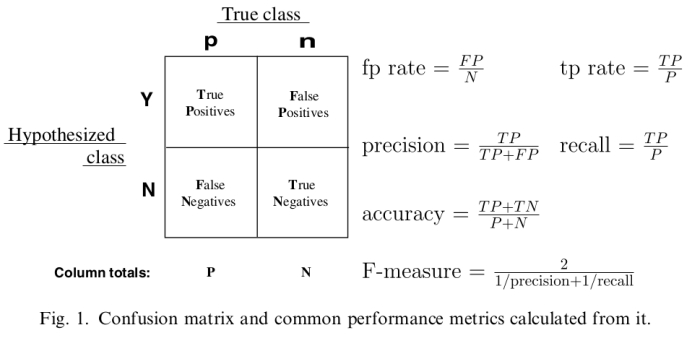
对以上混淆矩阵的解释：

P：样本数据中的正例数。

N：样本数据中的负例数。

Y：通过模型预测出来的正例数。

N：通过模型预测出来的负例数。

True Positives:真阳性，表示实际是正样本预测成正样本的样本数。

Falese Positives:假阳性，表示实际是负样本预测成正样本的样本数。

假阴性，表示实际是正样本预测成负样本的样本数。

True Negatives:真阴性，表示实际是负样本预测成负样本的样本数。

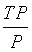:真阳性率(True Positive Rate，TPR)，也叫灵敏度(Sensitivity)，召回率(Recall)。即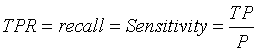：，正确的预测出的正例数占样本中正例总数的比例。真阳性率越大越好，越大代表在正样本中预测为正例的越多。

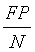:假阳性率(False Positive Rate，FPR)，也叫误诊率。错误的预测出的正例数占样本中负例的比例。假阳性率越小越好，越小代表在负样本中预测为正例的越少。

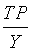:正确率(Precision),也叫精确率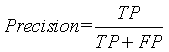，，通过模型预测出来真正是正例的正例数占模型预测出来是正例数的比例，越大越好。

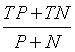:准确率(accuracy)，,模型预测正确的例数占总样本的比例。越大越好。

决策树

决策树(Decision Tree）是在已知各种情况发生概率的基础上，通过构成决策树来求取净现值的期望值大于等于零的概率，评价项目风险，判断其可行性的决策分析方法，是直观运用概率分析的一种图解法。由于这种决策分支画成图形很像一棵树的枝干，故称决策树。在机器学习中，决策树是一个预测模型，他代表的是对象属性与对象值之间的一种映射关系。Entropy = 系统的凌乱程度，使用算法ID3, C4.5和C5.0生成树算法使用熵。这一度量是基于信息学理论中熵的概念。

随机森林

随机森林指的是利用多棵树对样本进行训练并预测的一种分类器。该分类器最早由Leo Breiman和Adele Cutler提出，并被注册成了商标。

系列传送门