2019南京部分题解
A 签到
B
题目大意
粉刷一个n行m列矩形，每次只能粉刷相邻的没有走过的格子并且每刷一个格子都是合法的，一个合法的粉刷路径是指：对于任意两个被粉刷的格子来说，只走粉刷过的格子的最短路径与他们的曼哈顿距离相等。问你粉刷完所有格子有多少种方法。
解题思路
首先可以发现粉刷的图形不可能是凹的，凹出来的那两边的点的最短距离肯定会被改变，当然也不可能是空心的，所以可以把所有的合法路径看是每次逐渐的扩充一行或者一列。从矩形中随意选中一个点扩充，可以扩充n-1行和m-1列，方案数就是c(n+m-2, n-1)，但是一乘发现不太对，对于一个固定的方案来说，起始的点一定能随便选吗？
考虑像上面所说的那样扩充，对于一个固定的方案来说，终点必定是一个角落，而如果固定这个角落，通过固定的方案我们可以倒推出起点也是固定的，所以我们其实不用纠结起点问题，我们就固定四个终点，求走到四个终点的方案数，答案就是\(4 \times c(n+m-2, n-1)\)，注意给出的矩形是一条直线的话，只有两个角，而且中间不能交叉走，答案固定是2。
代码
const int maxn = 2e6+10;
const int maxm = 1e6+10;
int f[maxn], inv[maxn];
int qp(ll x, ll y) {
ll res = 1;
while(y) {
if (y&1) res = res*x%MOD;
x = x*x%MOD;
y >>= 1;
}
return res;
}
int main() {
IOS;
f[0] = 1;
for (int i = 1; i<maxn; ++i) f[i] = 1ll*f[i-1]*i%MOD;
inv[maxn-1] = qp(f[maxn-1], MOD-2);
for (int i = maxn-2; i>=0; --i) inv[i] = 1ll*inv[i+1]*(i+1)%MOD;
int __; cin >> __;
while(__--) {
int n, m; cin >> n >> m;
if (n==1 || m==1) cout << 2 << endl;
else cout << 4ll*f[m+n-2]%MOD*inv[n-1]%MOD*inv[m-1]%MOD << endl;
}
return 0;
}
C
解题思路
可以根据相邻方格之间的关系建图，建出来的是若干个拓扑图，每个拓扑图dfs一下回溯的时候计数即可。
代码
const int maxn = 1e3+10;
const int maxm = 2e6+10;
int dx[] = {0, 0, -1, 1};
int dy[] = {-1, 1, 0, 0};
int n, m, g[maxn][maxn], in[maxm];
vector<int> e[maxm];
ll calc[maxm][4];
int to(int x, int y) {
return (x-1)*m+y;
}
int vis[maxm];
void dfs(int u) {
//cout << u << endl;
if (vis[u]) return;
if (e[u].empty()) {
calc[u][0] = 1;
return;
}
vis[u] = 1;
for (auto v : e[u]) {
dfs(v);
for (int i = 1; i<=3; ++i) calc[u][i] = (calc[u][i]+calc[v][i-1])%MOD;
calc[u][3] = (calc[u][3]+calc[v][3])%MOD;
}
}
int main() {
IOS;
cin >> n >> m;
for (int i = 1; i<=n; ++i)
for (int j = 1; j<=m; ++j)
cin >> g[i][j];
for (int i = 1; i<=n; ++i)
for (int j = 1; j<=m; ++j)
for (int k = 0; k<4; ++k) {
int xx = i+dx[k], yy = j+dy[k];
if (xx>=1 && xx<=n && yy>=1 && yy<=m && g[i][j]+1==g[xx][yy]) {
//cout << i << ' ' << j << ' ' << xx << ' ' << yy << endl;
e[to(i, j)].push_back(to(xx, yy));
++in[to(xx, yy)];
}
}
ll sum = 0;
for (int i = 1; i<=n*m; ++i)
if (!vis[i] && !in[i]) {
dfs(i);
sum = (sum+calc[i][3])%MOD;
//cout << i << ' ' << sum << endl;
}
cout << sum << endl;
return 0;
}
F
题目大意
给你n个字符串(可能重复)，然后m个操作。
操作1：交换两个位置的字符串
操作2：询问区间\([l,r]\)内在与给定字符串s的lcp至少为k位的字符串有多少个。
解题思路
这题的精妙之处在于，我们先对n个字符串建一棵trie，然后在遍历这棵trie的过程中，假设走到点p，点p的深度是d，那么以点p为根子树包含的字符串都是与给定s串至少匹配d位的字符串。对于查询操作，我们只要询问这棵子树内有多少范围在\([l,r]\)之间的字符串即可，可以用dfs序建主席树解决，如果再加上修改操作的话，就变成了在线维护二维信息的问题，可以用dfs序+树套树解决，这里我用的树状数组套+线段树动态开点。
写的时候还是遇到了一些问题，由于字符串可能是重复的，那么有可能字典树上的一个点对应多个下标，我一开始建树的时候第一维是dfs序，因为一个dfs序对应多个下标，所以很难做，后来把第一维改成了下标，第二维dfs序就好做了，每次修改都变成了单点修改。
代码
const int maxn = 2e5+10;
const int maxm = 1e6+10;
int n, m;
struct Node {
int l, r, sum;
} hjt[maxn*200];
int tot, rt[maxn];
int tr[maxn][26], idx, nd[maxn];
void insert(string s, int i) {
int p = 0;
for (auto ch : s) {
int t = ch-'a';
if (!tr[p][t]) tr[p][t] = ++idx;
p = tr[p][t];
}
nd[i] = p;
}
int dfn, id[maxn], id2[maxn];
void dfs(int u) {
id[u] = ++dfn;
for (int i = 0; i<26; ++i)
if (tr[u][i]) dfs(tr[u][i]);
id2[u] = dfn;
}
void update(int &now, int l, int r, int p, int v) {
if (!now) now = ++tot;
hjt[now].sum += v;
if (l==r) return;
int mid = (l+r)>>1;
if (p<=mid) update(hjt[now].l, l, mid, p, v);
else update(hjt[now].r, mid+1, r, p, v);
}
int query(int now, int l, int r, int L, int R) {
if (l>=L && r<=R) return hjt[now].sum;
int mid = (l+r)>>1; int sum = 0;
if (L<=mid) sum += query(hjt[now].l, l, mid, L, R);
if (R>mid) sum += query(hjt[now].r, mid+1, r, L, R);
return sum;
}
void add(int x, int f) {
int p = id[nd[x]];
while(x<=n) {
update(rt[x], 1, dfn, p, f);
x += x&-x;
}
}
int ask(int x, int l, int r) {
int sum = 0;
while(x) {
sum += query(rt[x], 1, dfn, l, r);
x -= x&-x;
}
return sum;
}
int find(string s, int k) {
if (!k) return 0;
int p = 0;
for (int i = 0; i<k; ++i) {
p = tr[p][s[i]-'a'];
if (!p) return -1;
}
return p;
}
int main() {
IOS;
cin >> n >> m;
for (int i = 1; i<=n; ++i) {
string s; cin >> s;
insert(s, i);
}
dfs(0);
for (int i = 1; i<=n; ++i) rt[i] = ++tot;
for (int i = 1; i<=n; ++i) add(i, 1);
int op, k, l, r;
while(m--) {
cin >> op;
if (op==1) {
cin >> l >> r;
if (l==r) continue;
add(l, -1);
add(r, -1);
swap(nd[l], nd[r]);
add(l, 1);
add(r, 1);
}
else {
string s; cin >> s;
cin >> k >> l >> r;
int t = find(s, k);
if (t==-1) cout << 0 << endl;
else cout << ask(r, id[t], id2[t])-ask(l-1, id[t], id2[t]) << endl;
}
}
return 0;
}
H
解题思路
人类智慧题，可惜我没有智慧orz....对于a，b，c三种人来说，因为c是随机的，所以可以把c归到b中去，对于三种问题来说，第一种问题和第二种没用，就只看第三种就行了，那么就只有a比b和c加起来都多的时候才有解，答案就是\(2 \times (b+c)+1\)。注意只有公主一个人的时候，输出0。
代码
int main() {
IOS;
int a, b, c; cin >> a >> b >> c;
if (a==1 && !b && !c) cout << "YES" << endl << 0 << endl;
else if (a>=(b+c)+1) cout << "YES" << endl << 2*(b+c)+1 << endl;
else cout << "NO" << endl;
return 0;
}
I
解题思路
a的范围只有50，肯定大有搞头，我们可以统计0到50中所有数字出现了多少次，每次选择比当前能量小的数字的时候，比如选择30，就是从所有值等于30的位置中挑一个，然后继续选，当选到能量大于等于50的时候就随便选了，而由于0对能量没有贡献而且可以随时选，可以单独拿出来计算。做法就是记忆化搜索，对于当前的状态，用哈希的方法来记录。
代码
const int maxn = 2e5+10;
const int maxm = 1e6+10;
int arr[maxn], f[maxn], inv[maxn];
struct S {
int a[51];
S (){clr(a, 0);};
};
int qp(ll x, ll y) {
ll res = 1;
while(y) {
if (y&1) res = res*x%MOD;
x = x*x%MOD;
y >>= 1;
}
return res;
}
unordered_map<ull, int> mp;
int dfs(int now, int cnt, S state) {
if (!cnt) return 1;
if (now>=50) return f[cnt];
ull h = 0;
for (int i = 1; i<=50; ++i) h = 1ull*h*P+state.a[i]+1;
if (mp.count(h)) return mp[h];
int ans = 0;
for (int i = now; i>=1; --i) {
if (!state.a[i]) continue;
--state.a[i];
ans = (ans+1ll*(state.a[i]+1)*dfs(now+i, cnt-1, state)%MOD)%MOD;
++state.a[i];
}
return mp[h] = ans;
}
int main() {
IOS;
int n; cin >> n;
S s;
for (int i = 0; i<=n; ++i) {
cin >> arr[i];
++s.a[arr[i]];
}
f[0] = 1;
for (int i = 1; i<maxn; ++i) f[i] = 1ll*f[i-1]*i%MOD;
inv[maxn-1] = qp(f[maxn-1], MOD-2);
for (int i = maxn-2; i>=0; --i) inv[i] = 1ll*inv[i+1]*(i+1)%MOD;
--s.a[arr[0]];
ll ans = dfs(arr[0], n-s.a[0], s);
ans = ans*f[n]%MOD*inv[n-s.a[0]]%MOD;
cout << ans << endl;
return 0;
}
J
解题思路
由于对战的对手是随机的，所有我们影响结果的决策就只有谁和谁组队，也就是找一个两两组队的方案，使得最终的期望值最大，我们可以枚举出b中的一个人跟c中的一个人组队，然后这两人组队的期望就是他们和a中的所有人打一场获得的奖励除以n，题目正好问的乘n的，所以也不用除了。我们算出来两人组队的期望了，题目让求所有人两两组队的期望，直接跑km就行了。
const int maxn = 4e2+10;
const int maxm = 1e6+10;
int visx[maxn], visy[maxn], pre[maxn], match[maxn];
int g[maxn][maxn], lx[maxn], ly[maxn], s[maxn];
int n, m;
void find(int k) {
int y = 0, p = 0; clr(pre, 0);
for (int i = 1; i<=m; ++i) s[i] = INF;
match[y] = k;
while(1) {
int x = match[y], d = INF; visy[y] = 1;
for (int i = 1; i<=m; ++i)
if (!visy[i]) {
if (s[i] > lx[x]+ly[i]-g[x][i])
s[i] = lx[x]+ly[i]-g[x][i], pre[i] = y;
if (d > s[i]) d = s[i], p = i;
}
for (int i = 0; i<=m; ++i) {
if (visy[i]) lx[match[i]] -= d, ly[i] += d;
else s[i] -= d;
}
y = p;
if (!match[y]) break;
}
while(y) match[y] = match[pre[y]], y = pre[y];
}
int km() {
clr(lx, 0x3f); clr(ly, 0); clr(match, 0);
for (int i = 1; i<=n; ++i) clr(visy, 0), find(i);
int ans = 0;
for (int i = 1; i<=m; ++i) ans += g[match[i]][i];
return ans;
}
ll a[maxn], b[maxn], c[maxn], d[maxn];
int main() {
IOS;
cin >> n; m = n;
for (int i = 1; i<=n; ++i) cin >> a[i];
for (int i = 1; i<=n; ++i) cin >> b[i];
for (int i = 1; i<=n; ++i) cin >> c[i];
for (int i = 1; i<=n; ++i) cin >> d[i];
for (int i = 1; i<=n; ++i)
for (int j = 1; j<=n; ++j)
for (int k = 1; k<=n; ++k)
if (c[i]+d[j]>a[k]) g[i][j] += b[k];
cout << km() << endl;
return 0;
}
K
解题思路
先找点p所在直线，然后找点p和三角形其中两个点构成的面积最大的三角形，根据这个三角形和原来三个点构成的三角形的面积比来算分割点。
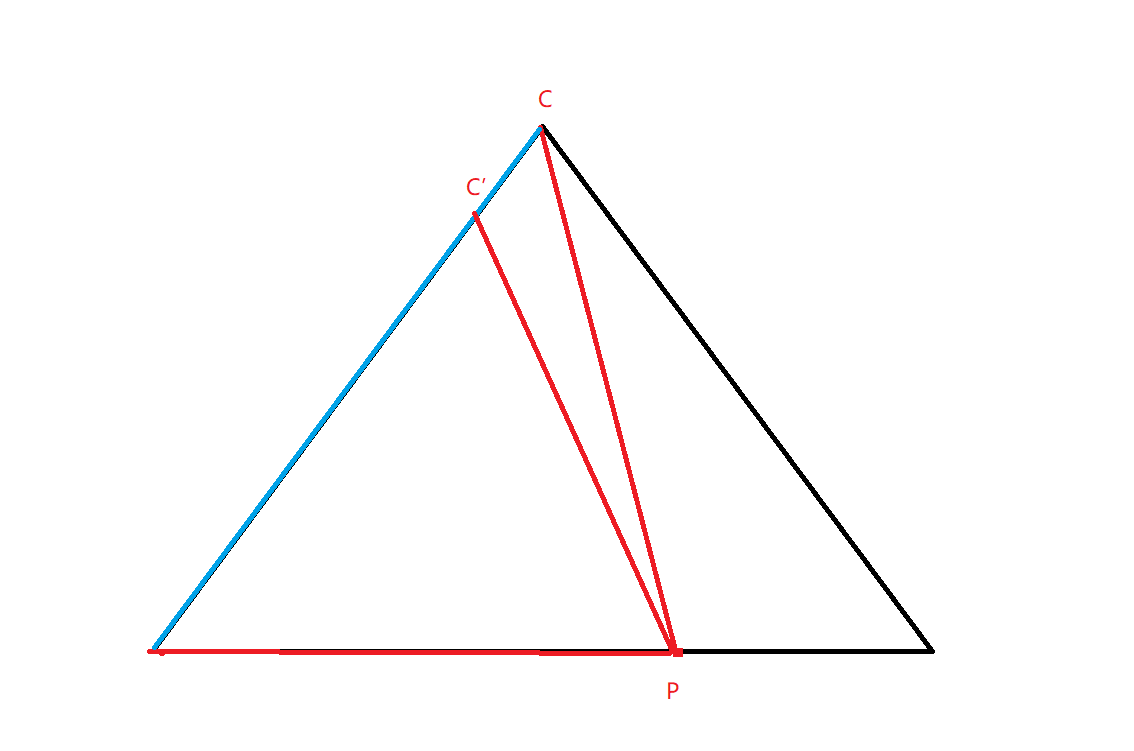
参考上图，主要思路就是移动点C，然后蓝线长度减少的百分比和三角形面积减少的百分比是一致的，注意点C必须是和点p不在一条直线上的那个点，除非点p在三角形端点，否则的话，会把三角形分成三块。
代码
const int maxn = 1e3+10;
const int maxm = 2e6+10;
int sgn(double x){
if(fabs(x) < eps) return 0;
return x<0 ? -1:1;
}
struct Point{
double x,y;
Point(){}
Point(double _x,double _y){
x = _x; y = _y;
}
Point operator -(const Point &b)const{
return Point(x-b.x,y-b.y);
}
double operator ^(const Point &b)const{
return x*b.y - y*b.x;
}
double operator *(const Point &b)const{
return x*b.x + y*b.y;
}
};
struct Line{
Point s,e;
Line(){}
Line(Point _s,Point _e){
s = _s; e = _e;
}
bool pointonseg(Point p){
return sgn((p-s)^(e-s)) == 0 && sgn((p-s)*(p-e)) <= 0;
}
};
double getS(Point a, Point b, Point c) {
Point vec1 = a-b;
Point vec2 = a-c;
return fabs(vec1^vec2)/2;
}
void getans(double S, Point a, Point b, Point c) {
double d = S/getS(a, b, c);
double dx = c.x-b.x, dy = c.y-b.y;
printf("%.7f %.7f\n", c.x-(1-d)*dx, c.y-(1-d)*dy);
}
int main() {
int __; cin >> __;
Point a, b, c, d, e, f;
while(__--) {
Point p[3], pp;
for (int i = 0; i<3; ++i) scanf("%lf %lf", &p[i].x, &p[i].y);
scanf("%lf %lf", &pp.x, &pp.y);
Line Le[3];
Le[0] = {p[0], p[1]};
Le[1] = {p[1], p[2]};
Le[2] = {p[0], p[2]};
double S = getS(p[0], p[1], p[2])/2;
//cout << S << endl;
if (Le[0].pointonseg(pp)) {
if (sgn(getS(pp, p[0], p[2])-S)>=0) getans(S, pp, p[0], p[2]);
else if (sgn(getS(pp, p[1], p[2])-S)>=0) getans(S, pp, p[1], p[2]);
else printf("-1\n");
}
else if (Le[1].pointonseg(pp)) {
if (sgn(getS(pp, p[0], p[1])-S)>=0) getans(S, pp, p[1], p[0]);
else if (sgn(getS(pp, p[0], p[2])-S)>=0) getans(S, pp, p[2], p[0]);
else printf("-1\n");
}
else if (Le[2].pointonseg(pp)) {
if (sgn(getS(pp, p[0], p[1])-S)>=0) getans(S, pp, p[0], p[1]);
else if (sgn(getS(pp, p[1], p[2])-S)>=0) getans(S, pp, p[2], p[1]);
else printf("-1\n");
}
else printf("-1\n");
}
return 0;
}
