算法模板整理V1.5
字符串
双哈希
Birthday Cake 给n个字符串,问每个字符串前后缀相等时,中间的串与其他字符串相等的个数。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll, ll> PLL;
const int p1 = 131;
const int p2 = 13331;
const int mod1 = 1e9+7;
const int mod2 = 1e9+9;
const int maxn = 4e5+10;
ll f1[maxn], f2[maxn], hs1[maxn], hs2[maxn];
string s[maxn]; map<PLL, int> mp;
int main() {
f1[0] = f2[0] = 1;
//hs1[0] = hs2[0] = 1这样写是错误的,在计算相同前后缀的时候,前缀前头多了一位1,后缀没有
for (int i = 1; i<maxn; ++i) {
f1[i] = f1[i-1]*p1%mod1;
f2[i] = f2[i-1]*p2%mod2;
}
ios::sync_with_stdio(0);
int n; cin >> n;
for (int i = 1; i<=n; ++i) cin >> s[i];
sort(s+1, s+n+1, [](string a, string b) {return a.size()<b.size();});
ll ans = 0;
for (int i = 1; i<=n; ++i) {
for (int j = 1; j<=s[i].size(); ++j) {
//注意string从0开始,这里的hs数组从1开始
hs1[j] = (hs1[j-1]*p1+s[i][j-1])%mod1;
hs2[j] = (hs2[j-1]*p2+s[i][j-1])%mod2;
cout << hs1[j] << ' ' << hs2[j] << endl;
}
int ed = s[i].size();
for (int l = 1; l<=s[i].size(); ++l) {
int r = ed-l+1;
if (r-1-l-1<0) break;
ll a1 = hs1[l];
ll a2 = hs2[l];
ll b1 = ((hs1[ed]-hs1[r-1]*f1[ed-r+1])%mod1+mod1)%mod1;
ll b2 = ((hs2[ed]-hs2[r-1]*f2[ed-r+1])%mod2+mod2)%mod2;
//对比前l位与后l位是否相同
cout << a1 << ' ' << b1 << endl;
cout << a2 << ' ' << b2 << endl;
if (a1==b1 && a2==b2) {
ll m1 = ((hs1[r-1]-hs1[l]*f1[r-1-l])%mod1+mod1)%mod1;
ll m2 = ((hs2[r-1]-hs2[l]*f2[r-1-l])%mod2+mod2)%mod2;
//求区间r-1到l+1的哈希值hs1[r-1]-hs1[l+1-1]*f1[r-1-(l+1-1)]
cout << m1 << ' ' << m2 << endl;
ans += mp[{m1, m2}];
}
}
ans += mp[{hs1[ed], hs2[ed]}];
++mp[{hs1[ed], hs2[ed]}];
cout << "___________" << endl;
}
cout << ans << endl;
return 0;
}
Trie
const int maxn = 1e5+10;
int idx, tr[maxn*30][2], f[maxn*30], cnt[maxn*30];
int n, k;
void insert(int num, int id) {
int p = 0;
for (int i = 30; i>=0; --i) {
int t = num>>i&1;
if (!tr[p][t]) tr[p][t] = ++idx;
p = tr[p][t];
++cnt[p]; //统计插入点的个数
}
f[p] = id;
}
int find(int num) { //查询最大异或值
int p = 0, tt = 0;
for (int i = 30; i>=0; --i) {
int t = num>>i&1;
if (tr[p][t^1]) tt ^= (1<<i), p = tr[p][t^1];
else p = tr[p][t];
}
return tt>=k ? f[p]:-1;
}
void del(int num) {
int p = 0;
for (int i = 30; i>=0; --i) {
int t = num>>i&1;
--cnt[tr[p][t]];
if (!cnt[tr[p][t]]) { //点数为0删除这个点
int res = p;
p = tr[p][t];
tr[res][t] = 0;
}
else p = tr[p][t];
}
}
acwing 143 01trie
const int maxn = 1e5+10;
const int maxm = 3e6+10;
int a[maxn], trie[maxm][2], tot, n;
void insert(int num) {
int p = 0;
for (int i = 30; i>=0; --i) {
int t = num>>i&1;
if (!trie[p][t]) trie[p][t] = ++tot;
p = trie[p][t];
}
}
ll solve(int x) {
ll res = 0, p = 0;
for (int i = 30; i>=0; --i) {
res <<= 1;
int t = x>>i&1;
if (trie[p][t^1]) {
res |= 1;
p = trie[p][t^1];
}
else p = trie[p][t];
}
return res;
}
int main() {
scanf("%d",&n);
for (int i = 0; i<n; ++i) {
scanf("%d",&a[i]);
insert(a[i]);
}
ll res = 0;
for (int i = 0; i<n; ++i) res = max(res,solve(a[i]));
printf("%lld\n",res);
return 0;
}
HDU 6955 找到一个最短的连续子序列,其异或和不小于k,按顺序插入每个点的前缀异或和,然后找所有的异或和大于k的位置,每找到一个删除一次并更新答案
const int maxn = 1e5+10;
int idx, tr[maxn*30][2], f[maxn*30], cnt[maxn*30];
int n, k, arr[maxn], vis[maxn];
void insert(int num, int id) {
int p = 0;
for (int i = 30; i>=0; --i) {
int t = num>>i&1;
if (!tr[p][t]) tr[p][t] = ++idx;
p = tr[p][t];
++cnt[p];
}
f[p] = id;
}
int find(int num) {
int p = 0, tt = 0;
for (int i = 30; i>=0; --i) {
int t = num>>i&1;
if (tr[p][t^1]) tt ^= (1<<i), p = tr[p][t^1];
else p = tr[p][t];
}
return tt>=k ? f[p]:-1;
}
void del(int num) {
int p = 0;
for (int i = 30; i>=0; --i) {
int t = num>>i&1;
--cnt[tr[p][t]];
if (!cnt[tr[p][t]]) {
int res = p;
p = tr[p][t];
tr[res][t] = 0;
}
else p = tr[p][t];
}
}
int main() {
IOS;
int __; cin >> __;
while(__--) {
idx = 0;
cin >> n >> k;
int sum = 0;
insert(0, 0);
int len = INF, ax = -INF, ay = INF;
for (int i = 1, a; i<=n; ++i) {
cin >> a;
sum ^= a;
int x = find(sum);
arr[i] = sum;
while(x!=-1) {
if (i-x<ay-ax) ax = x, ay = i;
vis[x] = 1;
del(arr[x]);
x = find(sum);
}
insert(sum, i);
}
if (ax==-INF) cout << -1 << endl;
else cout << ax+1 << ' ' << ay << endl;
for (int i = 1; i<=n; ++i) {
if (vis[i]) vis[i] = 0;
else del(arr[i]);
}
}
return 0;
}
可持久化trie
求一个数组的后缀异或上一个数的最大值
板子一
const int maxn = 6e5+10;
int n, m;
int arr[maxn], tr[maxn*25][2], maxid[maxn*25];
int rt[maxn], idx;
void insert(int i, int p, int q) {
for (int j = 23; j>=0; --j) {
maxid[q] = i; //当前的数最靠右的位置
int v = arr[i]>>j&1;
if (p) tr[q][v^1] = tr[p][v^1]; //不同的分支复制过来
tr[q][v] = ++idx; //当前的分支建一个新的
p = tr[p][v], q = tr[q][v];
}
}
int query(int p, int c, int lim) {
for (int i = 23; i>=0; --i) {
int v = c>>i&1;
if (maxid[tr[p][v^1]]>=lim) p = tr[p][v^1];
else p = tr[p][v];
}
return c^arr[maxid[p]];
}
int main() {
IOS;
int n, m; cin >> n >> m;
maxid[0] = -1;
rt[0] = ++idx;
insert(0, 0, rt[0]);
for (int i = 1, x; i<=n; ++i) {
cin >> x;
arr[i] = arr[i-1]^x; //将数组的前缀加入trie
rt[i] = ++idx;
insert(i, rt[i-1], rt[i]);
}
char op[2];
int l, r, x;
while(m--) {
cin >> op;
if (op[0]=='A') {
cin >> x;
++n;
arr[n] = arr[n-1]^x;
rt[n] = ++idx;
insert(n, rt[n-1], rt[n]);
}
else {
cin >> l >> r >> x;
cout << query(rt[r-1], arr[n]^x, l-1) << endl;
}
}
return 0;
}
板子二
const int maxn = 6e5+10;
int n, m;
int arr[maxn], tr[maxn*25][2], maxid[maxn*25], cnt[maxn*25];
int rt[maxn], idx;
void insert(int i, int p, int q) {
for (int j = 23; j>=0; --j) {
maxid[q] = i; //当前的数最靠右的位置
int v = arr[i]>>j&1;
if (p) tr[q][v^1] = tr[p][v^1]; //不同的分支复制过来
tr[q][v] = ++idx; //当前的分支建一个新的
p = tr[p][v], q = tr[q][v];
cnt[q] = cnt[p]+1;
}
}
int query(int p, int q, int c) {
for (int i = 23; i>=0; --i) {
int v = c>>i&1;
int t = tr[p][v^1];
if (cnt[tr[q][v^1]]-cnt[tr[p][v^1]]>0) {
q = tr[q][v^1], p = tr[p][v^1];
if (!v) c ^= 1<<i;
}
else {
q = tr[q][v], p = tr[p][v];
if (v) c ^= 1<<i;
}
//cout << c << endl;
//cout << maxid[q] << endl;
//cout << p << endl;
if (!q) break;
}
return c;
}
int main() {
IOS;
int n, m; cin >> n >> m;
maxid[0] = -1;
rt[0] = ++idx;
insert(0, 0, rt[0]);
for (int i = 1, x; i<=n; ++i) {
cin >> x;
arr[i] = arr[i-1]^x; //将数组的前缀加入trie
rt[i] = ++idx;
insert(i, rt[i-1], rt[i]);
}
char op[2];
int l, r, x;
while(m--) {
cin >> op;
if (op[0]=='A') {
cin >> x;
++n;
arr[n] = arr[n-1]^x;
rt[n] = ++idx;
insert(n, rt[n-1], rt[n]);
}
else {
cin >> l >> r >> x;
cout << query(l-2<0 ? 0:rt[l-2], rt[r-1], arr[n]^x) << endl;
}
}
return 0;
}
kmp
const int maxn = 1e6+10;
char str[maxn], sstr[maxn];
int len, slen, ans, nxt[maxn];
void get_next() {
int i = 0, j = -1;
nxt[i] = j;
while(i < len){
while( j != -1 && sstr[i] != sstr[j]) j = nxt[j];
nxt[++i] = ++j;
}
}
void kmp() {
get_next();
int i =0, j = 0;
while(i < len){
while(j != -1 && str[i] != sstr[j]) j = nxt[j];
++i, ++j;
if(j == slen) {
++ans;
//j = 0; 不允许重叠
}
}
}
HDU 1358 KMP求前缀的最小循环节以及循环次数
const int maxn = 2e6+10;
char str[maxn];
int n, nxt[maxn];
void get_next() {
int i = 0, j = -1;
nxt[i] = j;
while(i<n) {
while(~j && str[i]!=str[j]) j = nxt[j];
nxt[++i] = ++j;
}
}
int main(void) {
int kase = 1;
while(~scanf("%d", &n) && n) {
scanf("%s", str);
get_next();
printf("Test case #%d\n", kase++);
for (int i = 2; i<=n; ++i) {
int tmp = i-nxt[i];
if (nxt[i]>=1 && !(i%tmp)) printf("%d %d\n", i, i/tmp);
nxt[i] = 0;
}
putchar(endl);
}
return 0;
}
exkmp
nxt:字符串t与t的每一个后缀的lcp
ext:字符串s的每一个后缀与字符串t的lcp
void exkmp() {
nxt[1] = m;
for (int i = 2, l = 0, r = 0; i<=m; ++i) {
if (i<=r) nxt[i] = min(nxt[i-l+1], 1LL*r-i+1);
while(nxt[i]+i<=m && t[nxt[i]+1]==t[i+nxt[i]]) ++nxt[i];
if (r<i+nxt[i]-1) {
r = i+nxt[i]-1;
l = i;
}
}
for (int i = 1, l = 0, r = 0; i<=n; ++i) {
if (i<=r) ext[i] = min(nxt[i-l+1], 1LL*r-i+1);
while(ext[i]+i<=n && s[ext[i]+i]==t[ext[i]+1]) ++ext[i];
if (r<=i+ext[i]-1) {
r = i+ext[i]-1;
l = i;
}
}
}
HDU 6153 求t的每个后缀在s中出现的次数,把两个串都翻转一下就是求t的每个前缀在s中出现的次数
const int maxn = 1e6+10;
char s[maxn], t[maxn];
int m, n;
ll nxt[maxn], ext[maxn];
void exkmp() {
nxt[1] = m;
for (int i = 2, l = 0, r = 0; i<=m; ++i) {
if (i<=r) nxt[i] = min(nxt[i-l+1], 1LL*r-i+1);
while(nxt[i]+i<=m && t[nxt[i]+1]==t[i+nxt[i]]) ++nxt[i];
if (r<i+nxt[i]-1) {
r = i+nxt[i]-1;
l = i;
}
}
for (int i = 1, l = 0, r = 0; i<=n; ++i) {
if (i<=r) ext[i] = min(nxt[i-l+1], 1LL*r-i+1);
while(ext[i]+i<=n && s[ext[i]+i]==t[ext[i]+1]) ++ext[i];
if (r<=i+ext[i]-1) {
r = i+ext[i]-1;
l = i;
}
}
}
ll ff[maxn];
int main() {
IOS;
for (int i = 1; i<maxn; ++i) ff[i] = (ff[i-1]+i)%MOD;
int __; cin >> __;
while(__--) {
cin >> s+1 >> t+1;
clr(nxt, 0);
clr(ext, 0);
reverse(s+1, s+strlen(s+1)+1);
reverse(t+1, t+strlen(t+1)+1);
m = strlen(t+1);
n = strlen(s+1);
exkmp();
int len = strlen(s+1);
ll sum = 0;
for (int i = 1; i<=len; ++i) sum = (sum+ff[ext[i]])%MOD;
cout << sum << endl;
}
return 0;
}
manacher
char ma[maxn], str[maxn];
int ans, len, mp[maxn];
void manacher() {
int l = 0;
ma[l++] = '$', ma[l++] = '#';
for (int i = 0; i<len; ++i) {
ma[l++] = str[i];
ma[l++] = '#';
}
ma[l] = -1;
int id = 0, mx = 0;
for (int i = 0; i<l; ++i) {
mp[i] = mx>i ? min(mp[id*2-i], mx-i) : 1;
while(ma[i+mp[i]]==ma[i-mp[i]]) ++mp[i];
if (mx<i+mp[i]) {
mx = i+mp[i];
id = i;
}
}
}
HDU 5340 求是否能用三个回文串组成一个字符串
const int maxn = 1e5+10;
char ma[maxn], str[maxn];
int ans, len, mp[maxn], pre[maxn], post[maxn];
bool manacher() {
int l = 0;
ma[l++] = '$', ma[l++] = '#';
for (int i = 0; i<len; ++i) {
ma[l++] = str[i];
ma[l++] = '#';
}
ma[l] = '1';
int id = 0, mx = 0, k1 = 0, k2 = 0;
for (int i = 0; i<l; ++i) {
mp[i] = mx>i ? min(mp[id*2-i], mx-i) : 1;
while(ma[i+mp[i]]==ma[i-mp[i]]) ++mp[i];
if (mx<i+mp[i]) {
mx = i+mp[i];
id = i;
}
if (mp[i]>1 && i-mp[i]==0) pre[k1++] = i;
if (mp[i]>1 && i+mp[i]==l) post[k2++] = i;
}
for (int i = 0; i<k1; ++i)
for (int j = k2-1; j>=0; --j) {
int L = pre[i]+mp[pre[i]]-1, R = post[j]-mp[post[j]]+1;
if (L>=R) break;
int mid = (L+R)/2;
if (mp[mid]>1 && mid+mp[mid]-1>=R) return true;
}
return false;
}
int main(void) {
int t; scanf("%d", &t);
while(t--) {
scanf("%s", str);
len = strlen(str);
printf("%s\n", manacher()? "Yes":"No");
}
return 0;
}
ac自动机
const int maxn = 55*1e4+10;
const int maxm = 1e6+10;
int tr[maxn][26], cnt[maxn], fail[maxn], idx;
char str[maxm];
int n;
void init() {
idx = 0;
clr(tr, 0); clr(cnt, 0); clr(fail, 0);
}
void insert() {
int p = 0;
for (int i = 0; str[i]; ++i) {
int t = str[i]-'a';
if (!tr[p][t]) tr[p][t] = ++idx;
p = tr[p][t];
}
++cnt[p];
}
int q[maxn];
void build() {
int tt = -1, hh = 0;
for (int i = 0; i<26; ++i)
if (tr[0][i]) q[++tt] = tr[0][i];
while(hh<=tt) {
int t = q[hh++];
for (int i = 0; i<26; ++i) {
int p = tr[t][i];
/* trie树
if (p) {
int j = fail[t];
while(j && !tr[j][i]) j = fail[j];
if (tr[j][i]) j = tr[j][i];
fail[p] = j;
q[++tt] = p;
}
*/
//trie图 省略上面的循环,fail指针一步直接跳到最后的位置
if (!p) tr[t][i] = tr[fail[t]][i];
else {
fail[p] = tr[fail[t]][i];
q[++tt] = p;
}
}
}
}
int main(void) {
IOS;
int __; cin >> __;
while(__--) {
init();
cin >> n;
for (int i = 1; i<=n; ++i) {
cin >> str;
insert();
}
build();
cin >> str;
int ans = 0;
for (int i = 0, j = 0; str[i]; ++i) {
int t = str[i]-'a';
/*
while(j && !tr[j][t]) j = fail[j];
if (tr[j][t]) j = tr[j][t];
*/
j = tr[j][t];
int p = j;
while(p) {
ans += cnt[p];
cnt[p] = 0;
p = fail[p];
}
}
cout << ans << endl;
}
return 0;
}
后缀数组
const int maxn = 1e6+10;
int n, m;
char s[maxn];
int sa[maxn], x[maxn], y[maxn], c[maxn], rk[maxn], h[maxn];
void get_sa() {
for (int i = 1; i<=n; ++i) ++c[x[i]=s[i]]; //第一遍基数排序,x[i]按字符串的ascall码排序
for (int i = 2; i<=m; ++i) c[i] += c[i-1];
for (int i = n; i; --i) sa[c[x[i]]--] = i; //倒序枚举保证稳定排序
for (int k = 1; k<=n; k<<=1) {
int num = 0; //根据第一关键字求出第二关键字
for (int i = n-k+1; i<=n; ++i) y[++num] = i; //没有第二关键字的下标排前面
for (int i = 1; i<=n; ++i)
if (sa[i]>k) y[++num] = sa[i]-k;
//按排名将第二关键字对应的下标存到y里头,j+k的位置在sa[i],那么j的位置自然就在sa[i]-k了(根据j+k对j排序)
for (int i = 1; i<=m; ++i) c[i] = 0;
for (int i = 1; i<=n; ++i) ++c[x[i]]; //这里排序主要是排第一关键字相同的后缀
for (int i = 2; i<=m; ++i) c[i] += c[i-1];
for (int i = n; i; --i) sa[c[x[y[i]]]--] = y[i], y[i] = 0; //将第一关键字相同的按第二关键字排序
swap(x, y);
x[sa[1]] = 1, num = 1; //y现在是之前的第一关键字,用y来更新新的第一关键字x
for (int i = 2; i<=n; ++i)
x[sa[i]] = (y[sa[i]]==y[sa[i-1]] && y[sa[i]+k]==y[sa[i-1]+k]) ? num:++num;
if (num==n) break; //后缀的字典序不可能相同(长度就不同),如果排名都不同说明已经把所有后缀都排出来了
m = num;
}
}
void get_h() {
for (int i = 1; i<=n; ++i) rk[sa[i]] = i;
//排名为i的后缀排名是i,其实就是下标和排名对应的关系,和sa是反过来的
for (int i = 1, k = 0; i<=n; ++i) {
if (rk[i]==1) continue;
if (k) --k;
//设h[i] = hight[rk[i]], 即后缀i和排名在它前一位的lcp,h[i]>=h[i-1]-1,i从1到n枚举就能递推出来hight
int j = sa[rk[i]-1]; //排名为rk[i]-1的后缀的下标
while(i+k<=n && j+k<=n && s[i+k]==s[j+k]) ++k;
h[rk[i]] = k; //这个h是hight数组,不是h数组(偷懒
}
}
int main() {
IOS;
cin >> s+1;
n = strlen(s+1), m = 122;
get_sa(); get_h();
for (int i = 1; i<=n; ++i) cout << sa[i] << (i==n ? '\n':' ');
for (int i = 1; i<=n; ++i) cout << h[i] << (i==n ? '\n':' ');
return 0;
}
bzoj3238 设i为下标i为首字符的后缀,求\(\sum len(i)+len(j)+lcp(i,j) \ (1\leq i < j \leq n)\)
后缀数组+单调栈。前面的部分可以直接求,关键是如何快速求后半部分,我们知道两个后缀之间的lcp即他们之间的height数组的最小值。由于题目是对不同的数对计数,我们可以把后缀按照rk重新排序,每次计算当前的后缀j与它前面的后缀i的lcp,不难发现从j到i的过程中对height取min,得到的最小值是一块一块的,我们可以用单调栈算出每一块以当前下标j为右端点,以height[j]为区间最小值能扩展到的最小左端点l[j],然后用dp的思想就能根据l[j]递推出当前的后缀与排名在他前面的后缀的lcp之和。
const int maxn = 1e6+10;
int n, m;
char s[maxn];
int sa[maxn], x[maxn], y[maxn], c[maxn], rk[maxn], h[maxn];
void get_sa() {
for (int i = 1; i<=n; ++i) ++c[x[i]=s[i]];
for (int i = 2; i<=m; ++i) c[i] += c[i-1];
for (int i = n; i; --i) sa[c[x[i]]--] = i;
for (int k = 1; k<=n; k<<=1) {
int num = 0;
for (int i = n-k+1; i<=n; ++i) y[++num] = i;
for (int i = 1; i<=n; ++i)
if (sa[i]>k) y[++num] = sa[i]-k;
for (int i = 1; i<=m; ++i) c[i] = 0;
for (int i = 1; i<=n; ++i) ++c[x[i]];
for (int i = 1; i<=m; ++i) c[i] += c[i-1];
for (int i = n; i; --i) sa[c[x[y[i]]]--] = y[i], y[i] = 0;
swap(x, y);
x[sa[1]] = 1, num = 1;
for (int i = 2; i<=n; ++i)
x[sa[i]] = (y[sa[i]]==y[sa[i-1]] && y[sa[i]+k]==y[sa[i-1]+k]) ? num : ++num;
if (num==n) break;
m = num;
}
}
void get_h() {
for (int i = 1; i<=n; ++i) rk[sa[i]] = i;
for (int i = 1, k = 0; i<=n; ++i) {
if (rk[i]==1) continue;
if (k) --k;
int j = sa[rk[i]-1];
while(i+k<=n && j+k<=n && s[i+k]==s[j+k]) ++k;
h[rk[i]] = k;
}
}
stack<int> sk;
int l[maxn]; ll lcp[maxn];
int main() {
IOS;
cin >> s+1;
n = strlen(s+1); m = 122;
get_sa(); get_h();
h[0] = -1;
for (int i = n; i>=0; --i) {
while(!sk.empty() && h[sk.top()]>h[i]) {
l[sk.top()] = i;
sk.pop();
}
sk.push(i);
}
ll sum = 0;
for (int i = 1; i<=n; ++i) {
lcp[i] = lcp[l[i]]+2LL*(i-l[i])*h[i];
sum += 1LL*(n-1)*(n-i+1)-lcp[i];
}
cout << sum << endl;
return 0;
}
bzoj3998 求(可/不可)重复第k小子串
可以用二分求出可重复的第k小对应的不可重复的第k'小子串。
const int maxn = 1e6+10;
char s[maxn];
int n, m;
ll sum[maxn], sum2[maxn];
int sa[maxn], x[maxn], y[maxn], c[maxn], rk[maxn], h[maxn];
void get_sa() {
for (int i = 1; i<=n; ++i) ++c[x[i]=s[i]];
for (int i = 2; i<=m; ++i) c[i] += c[i-1];
for (int i = n; i; --i) sa[c[x[i]]--] = i;
for (int k = 1; k<=n; k<<=1) {
int num = 0;
for (int i = n-k+1; i<=n; ++i) y[++num] = i;
for (int i = 1; i<=n; ++i)
if (sa[i]>k) y[++num] = sa[i]-k;
for (int i = 1; i<=m; ++i) c[i] = 0;
for (int i = 1; i<=n; ++i) ++c[x[i]];
for (int i = 1; i<=m; ++i) c[i] += c[i-1];
for (int i = n; i; --i) sa[c[x[y[i]]]--] = y[i], y[i] = 0;
swap(x, y);
x[sa[1]] = 1, num = 1;
for (int i = 2; i<=n; ++i)
x[sa[i]] = (y[sa[i]]==y[sa[i-1]] && y[sa[i]+k]==y[sa[i-1]+k]) ? num : ++num;
if (num==n) break;
m = num;
}
}
void get_h() {
for (int i = 1; i<=n; ++i) rk[sa[i]] = i;
for (int i = 1, k = 0; i<=n; ++i) {
if (rk[i]==1) continue;
if (k) --k;
int j = sa[rk[i]-1];
while(i+k<=n && j+k<=n && s[i+k]==s[j+k]) ++k;
h[rk[i]] = k;
}
}
int k;
void solve0() {
for (int i = 1; i<=n; ++i) {
if (k>(n-sa[i]+1-h[i])) k -= (n-sa[i]+1-h[i]);
else {
for (int j = sa[i]; j<=sa[i]+h[i]+k-1; ++j) cout << s[j];
cout << endl;
return;
}
}
cout << -1 << endl;
}
int check(ll x) {
int l = 1, r = n;
while(l<r) {
int mid = (l+r)>>1;
if (sum[mid]>=x) r = mid;
else l = mid+1;
}
ll lcp = x+h[l]-sum[l-1], tot = lcp+sum2[l-1];
for (int i = l+1; i<=n; ++i) {
lcp = min(lcp, 1LL*h[i]);
if (!lcp) break;
tot += lcp;
if (tot>=k) return 1;
}
return 0;
}
void solve1() {
if (k>sum2[n]) {
cout << -1 << endl;
return;
}
int l = 1, r = k;
while(l<r) {
int mid = (l+r)>>1;
if (check(mid)) r = mid;
else l = mid+1;
}
k = l;
solve0();
}
int main() {
IOS;
cin >> s+1;
n = strlen(s+1); m = 122;
get_sa(); get_h();
for (int i = 1; i<=n; ++i) {
sum[i] = sum[i-1]+n-sa[i]+1-h[i];
sum2[i] = sum2[i-1]+n-sa[i]+1;
}
int t; cin >> t >> k;
if (!t) solve0();
else solve1();
return 0;
}
HDU 6704 给你一个字符串,问substr(l,r)第k次出现时的首字符的下标。
对于所有满足条件的子串,以其首字母开头的所有后缀的lcp一定都是大于等于这个子串长度的,根据lcp的性质,\(lcp(i, j) = min(lcp(k_1, k_2)), i \leq k_1,k_2 \leq j\)。我们可以得到如果将所有子串按字典序排序,则所有满足条件的后缀必定是一个连续区间,那么第k次出现的下标就是这个区间第k小的数。
const int maxn = 1e5+10;
char s[maxn];
int n, m;
int sa[maxn], x[maxn], y[maxn], c[maxn];
void get_sa() {
for (int i = 1; i<=n; ++i) ++c[x[i]=s[i]];
for (int i = 2; i<=m; ++i) c[i] += c[i-1];
for (int i = n; i; --i) sa[c[x[i]]--] = i;
for (int k = 1; k<=n; k<<=1) {
int num = 0;
for (int i = n-k+1; i<=n; ++i) y[++num] = i;
for (int i = 1; i<=n; ++i)
if (sa[i]>k) y[++num] = sa[i]-k;
for (int i = 1; i<=m; ++i) c[i] = 0;
for (int i = 1; i<=n; ++i) ++c[x[i]];
for (int i = 2; i<=m; ++i) c[i] += c[i-1];
for (int i = n; i; --i) sa[c[x[y[i]]]--] = y[i], y[i] = 0;
swap(x, y);
x[sa[1]] = 1, num = 1;
for (int i = 2; i<=n; ++i)
x[sa[i]] = (y[sa[i]]==y[sa[i-1]] && y[sa[i]+k]==y[sa[i-1]+k]) ? num:++num;
if (num==n) break;
m = num;
}
}
int rk[maxn], h[maxn];
void get_h() {
for (int i = 1; i<=n; ++i) rk[sa[i]] = i;
for (int i = 1, k = 0; i<=n; ++i) {
if (rk[i]==1) continue;
if (k) --k;
int j = sa[rk[i]-1];
while(i+k<=n && j+k<=n && s[i+k]==s[j+k]) ++k;
h[rk[i]] = k;
}
}
int f[maxn][20], lg[maxn];
void build() {
for (int i = n; i; --i) {
f[i][0] = h[i];
for (int j = 1; j<21; ++j)
if (i+(1<<j-1)<=n) f[i][j] = min(f[i][j-1], f[i+(1<<j-1)][j-1]);
}
for (int i = 2; i<=n; ++i) lg[i] = lg[i/2]+1;
}
int query(int l, int r) {
if (l>r) return INF;
int len = r-l+1;
int k = lg[len];
return min(f[l][k], f[r-(1<<k)+1][k]);
}
struct Node {
int l, r, sum;
} hjt[maxn*40];
int tot, rt[maxn];
void init() {
tot = 0;
clr(c, 0); clr(h, 0);
}
void insert(int pre, int &now, int l, int r, int pos) {
now = ++tot;
hjt[now] = hjt[pre];
++hjt[now].sum;
int mid = (l+r)>>1;
if (l==r) return;
if (pos<=mid) insert(hjt[pre].l, hjt[now].l, l, mid, pos);
else insert(hjt[pre].r, hjt[now].r, mid+1, r, pos);
}
int ask(int pre, int now, int l, int r, int k) {
if (l==r) return l;
int mid = (l+r)>>1;
int t = hjt[hjt[now].l].sum-hjt[hjt[pre].l].sum;
if (k<=t) return ask(hjt[pre].l, hjt[now].l, l, mid, k);
else return ask(hjt[pre].r, hjt[now].r, mid+1, r, k-t);
}
int main() {
IOS;
int __; cin >> __;
while(__--) {
init();
int q; cin >> n >> q;
cin >> s+1;
m = 122;
get_sa(); get_h(); build();
//for (int i = 1; i<=n; ++i) cout << h[i] << ' ' << rk[i] << endl;
for (int i = 1; i<=n; ++i) insert(rt[i-1], rt[i], 1, n, sa[i]);
while(q--) {
int ql, qr, k; cin >> ql >> qr >> k;
//cout << ql << endl;
int len = qr-ql+1;
int t = rk[ql];
int L = 1, R = t-1;
while(L<R) {
int mid = (L+R)>>1;
if (query(mid+1, t)>=len) R = mid;
else L = mid+1;
}
int l = L;
if (query(L+1, t)<len) ++l;
L = t+1, R = n;
while(L<R) {
int mid = (L+R+1)>>1;
if (query(t+1, mid)>=len) L = mid;
else R = mid-1;
}
int r = R;
if (query(t+1, r)<len) --r;
if (l>r && k==1) {
cout << ql << endl;
continue;
}
if (r-l+1<k) cout << -1 << endl;
else cout << ask(rt[l-1], rt[r], 1, n, k) << endl;
}
}
return 0;
}
数据结构
st表
const int maxn = 4e5+10;
const int maxm = 1e6+10;
int n, m, a[maxn], f[maxn][21], log2[maxn];
void build() {
for (int i = n; i>=1; --i) {
f[i][0] = a[i];
for (int j = 1; j<21; ++j)
if (i+(1<<j)-1<maxn) f[i][j] = max(f[i][j-1], f[i+(1<<j-1)][j-1]);
}
for (int i = 2; i <= n; ++i) Log2[i] = Log2[i / 2] + 1;
}
int query(int l, int r) {
int len = r-l+1;
int k = log2[len];
return max(f[l][k], f[r-(1<<k)+1][k]);
}
莫队
const int maxn = 2e5+10;
ll ans[maxn], res;
int arr[maxn], cnt[maxn*5], sz;
struct Q {
int l, r, i;
} q[maxn];
inline void add(int p) {
}
inline void sub(int p) {
}
int main(void) {
int n, m; scanf("%d%d", &n, &m);
sz = sqrt(n)+eps;
for (int i = 1; i<=n; ++i) scanf("%lld", &arr[i]);
for (int i = 0; i<m; ++i) scanf("%d%d", &q[i].l, &q[i].r), q[i].i = i;
sort(q, q+m, [](Q x, Q y) {return (x.l/sz^y.l/sz) ? x.l/sz < y.l/sz : ( ((x.l/sz)&1) ? x.r<y.r : x.r>y.r);});
//return x.l/sz == y.l/sz ? x.r < y.r : x.l/sz < y.l/sz; 普通排序,换成上面的奇偶排序一般快一些
int l = 1, r = 0;
for (int i = 0; i<m; ++i) {
while(q[i].r > r) add(++r);
while(q[i].l > l) sub(l++);
while(q[i].r < r) sub(r--);
while(q[i].l < l) add(--l);
ans[q[i].i] = res;
}
for (int i = 0; i<m; ++i) printf("%lld\n", ans[i]);
return 0;
}
CodeForces 617E 已知一个长度为 n 的整数数列 a[1],a[2],…,a[n] ,给定查询参数 l、r ,问在 [l,r] 区间内,有多少连续子段满足异或和等于 k 。也就是说,对于所有的 x,y (l≤x≤y≤r),能够满足a[x]a[x+1]…^a[y]=k的x,y有多少组。
const int maxn = 1e5+10;
ll cnt[maxn*100], ans[maxn], sz;
ll arr[maxn], res, k;
struct Q {
int l, r, i;
} q[maxn];
inline void add(int p) {
res += cnt[arr[p]^k];
++cnt[arr[p]];
}
inline void sub(int p) {
--cnt[arr[p]];
res -= cnt[arr[p]^k];
}
int main(void) {
int n, m;
scanf("%d%d%lld", &n, &m, &k);
for (int i = 1; i<=n; ++i) scanf("%lld", &arr[i]), arr[i] ^= arr[i-1];
for (int i = 0; i<m; ++i) scanf("%d%d", &q[i].l, &q[i].r), q[i].i = i;
sz = sqrt(n)+eps;
sort(q, q+m, [](Q x, Q y) {return (x.l/sz^y.l/sz) ? x.l/sz < y.l/sz : ( ((x.l/sz)&1) ? x.r<y.r : x.r>y.r);});
cnt[0] = 1; int l = 1, r = 0;
for (int i = 0; i<m; ++i) {
while(q[i].l < l) add(--l-1);
while(q[i].r > r) add(++r);
while(q[i].l > l) sub(l++-1);
while(q[i].r < r) sub(r--);
//因为用的前缀和,判断消去k能否到前缀异或和arr[l-1]所以要记得-1
ans[q[i].i] = res;
}
for (int i = 0; i<m; ++i) printf("%lld\n", ans[i]);
return 0;
}
CodeForces 86D 给定一个长度N的数组a, 询问区间1<=L<=R<=N中,每个数字出现次数的平方与当前数字的乘积和
const int maxn = 2e5+10;
ll ans[maxn], res;
int arr[maxn], cnt[maxn*5], sz;
struct Q {
int l, r, k;
} q[maxn];
inline void add(int p) {
++cnt[arr[p]];
res += 1LL * cnt[arr[p]]*cnt[arr[p]]*arr[p];
res -= 1LL * (cnt[arr[p]]-1)*(cnt[arr[p]]-1)*arr[p];
}
inline void sub(int p) {
res -= 1LL * cnt[arr[p]] * cnt[arr[p]] * arr[p];
res += 1LL * (cnt[arr[p]]-1)*(cnt[arr[p]]-1)*arr[p];
--cnt[arr[p]];
}
int main(void) {
int n, m; scanf("%d%d", &n, &m);
sz = sqrt(n)+eps;
for (int i = 1; i<=n; ++i) scanf("%lld", &arr[i]);
for (int i = 0; i<m; ++i) {
scanf("%d%d", &q[i].l, &q[i].r);
q[i].k = i;
}
sort(q, q+m, [=](Q x, Q y) {return (x.l/sz^y.l/sz) ? x.l/sz<y.l/sz : ((x.l/sz)%2 ? x.r<y.r:x.r>y.r);});
//return x.l/sz == y.l/sz ? x.r < y.r : x.l/sz < y.l/sz;
int l = 1, r = 0;
for (int i = 0; i<m; ++i) {
while(q[i].r > r) add(++r);
while(q[i].l > l) sub(l++);
while(q[i].r < r) sub(r--);
while(q[i].l < l) add(--l);
ans[q[i].k] = res;
}
for (int i = 0; i<m; ++i) printf("%lld\n", ans[i]);
return 0;
}
线段树
普通操作
bzoj 1230 区间异或
const int maxn = 1e5+10;
int n, m;
struct Tree {
int l, r, sum, lz;
} tree[maxn<<2];
inline void push_up(int rt) {
tree[rt].sum = tree[rt<<1].sum+tree[rt<<1|1].sum;
}
inline void push_down(int rt) {
if (tree[rt].lz==1) {
int len = tree[rt].r-tree[rt].l+1;
tree[rt<<1].sum = (len-(len>>1))-tree[rt<<1].sum;
tree[rt<<1|1].sum = (len>>1)-tree[rt<<1|1].sum;
if (tree[rt<<1].lz==-1) tree[rt<<1].lz = 1;
else tree[rt<<1].lz ^= 1;
if (tree[rt<<1|1].lz==-1) tree[rt<<1|1].lz = 1;
else tree[rt<<1|1].lz ^= 1;
}
tree[rt].lz = -1;
}
void build(int rt, int l, int r) {
tree[rt].l = l, tree[rt].r = r; tree[rt].lz = -1; tree[rt].sum = 0;
if (l==r) return;
int mid = (l+r)>>1;
build(rt<<1, l, mid);
build(rt<<1|1, mid+1, r);
}
void update(int rt, int l, int r) {
if (tree[rt].l>=l && tree[rt].r<=r) {
int len = tree[rt].r-tree[rt].l+1;
tree[rt].sum = len-tree[rt].sum;
if (tree[rt].lz==-1) tree[rt].lz = 1;
else tree[rt].lz ^= 1;
return;
}
push_down(rt);
int mid = (tree[rt].l+tree[rt].r)>>1;
if (l<=mid) update(rt<<1, l, r);
if (r>mid) update(rt<<1|1, l, r);
push_up(rt);
}
int ask(int rt, int l, int r) {
if (tree[rt].l>=l && tree[rt].r<=r) return tree[rt].sum;
int sum = 0;
int mid = (tree[rt].l+tree[rt].r)>>1;
push_down(rt);
if (l<=mid) sum += ask(rt<<1, l, r);
if (r>mid) sum += ask(rt<<1|1, l, r);
push_up(rt);
return sum;
}
int main() {
cin >> n >> m;
build(1, 1, n);
for (int i = 0, a, b, c; i<m; ++i) {
scanf("%d%d%d", &a, &b, &c);
if (a) printf("%d\n", ask(1, b, c));
else update(1, b, c);
}
return 0;
}
区间gcd
//gcd(a, b, c, d...) = gcd(a, c-b, d-c, e-d...)
//线段树维护差分数组求a和差分数组区间l+1和r的gcd的gcd
const int maxn = 1e6+10;
const int maxm = 1e6+10;
ll sub[maxn];
struct Node {
ll s, g;
} tree[maxn<<2];
inline void push_up(int rt) {
tree[rt].s = tree[rt<<1].s+tree[rt<<1|1].s;
tree[rt].g = __gcd(tree[rt<<1].g, tree[rt<<1|1].g);
}
void build(int rt, int l, int r) {
if (l==r) {
tree[rt].s = tree[rt].g = sub[l];
return;
}
int mid = (l+r)>>1;
build(rt<<1, l, mid);
build(rt<<1|1, mid+1, r);
push_up(rt);
}
void update(int rt, int l, int r, int pos, ll x) {
if (l==r) {
tree[rt].s += x;
tree[rt].g = tree[rt].s;
return;
}
int mid = (l+r)>>1;
if (pos<=mid) update(rt<<1, l, mid, pos, x);
else update(rt<<1|1, mid+1, r, pos, x);
push_up(rt);
}
ll ask1(int rt, int l, int r, int L, int R) {
if (l>=L && r<=R) return tree[rt].s;
int mid = (l+r)>>1;
ll sum = 0;
if (L<=mid) sum += ask1(rt<<1, l, mid, L, R);
if (R>mid) sum += ask1(rt<<1|1, mid+1, r, L, R);
return sum;
}
ll ask2(int rt, int l, int r, int L, int R) {
if (l>=L && r<=R) return tree[rt].g;
int mid = (l+r)>>1;
ll g = 0;
if (L<=mid) g = __gcd(g, ask2(rt<<1, l, mid, L, R));
if (R>mid) g = __gcd(g, ask2(rt<<1|1, mid+1, r, L, R));
return g;
}
int main() {
IOS;
int n, m; cin >> n >> m;
for (int i = 1; i<=n; ++i) cin >> sub[i];
for (int i = n; i>=1; --i) sub[i] -= sub[i-1];
build(1, 1, n);
while(m--) {
string str; int l, r, num;
cin >> str >> l >> r;
if (str[0]=='Q') {
ll a1 = ask1(1, 1, n, 1, l);
if (l==r) cout << a1 << endl;
else {
ll ans = __gcd(a1, abs(ask2(1, 1, n, l+1, r)));
cout << ans << endl;
}
}
else {
cin >> num;
update(1, 1, n, l, num);
if (r+1<=n) update(1, 1, n, r+1, -num);
}
}
return 0;
}
维护区间加和区间乘
acwing 1277
const int maxn = 2e5+10;
ll p;
struct Node {
ll val, lz1, lz2;
} tree[maxn<<2];
inline void push_up(int rt) {
tree[rt].val = (tree[rt<<1].val+tree[rt<<1|1].val)%p;
}
inline void push_down(int rt, ll l, ll r) {
if (tree[rt].lz1!=1 || tree[rt].lz2!=0) {
Node &ls = tree[rt<<1];
Node &rs = tree[rt<<1|1];
ll mul = tree[rt].lz1;
ll add = tree[rt].lz2;
ls.val = (ls.val*mul%p+(r-l+1-(r-l+1)/2)*add%p)%p;
rs.val = (rs.val*mul%p+(r-l+1)/2*add%p)%p;
ls.lz1 = ls.lz1*mul%p;
rs.lz1 = rs.lz1*mul%p;
ls.lz2 = (ls.lz2*mul%p+add)%p;
rs.lz2 = (rs.lz2*mul%p+add)%p;
tree[rt].lz1 = 1;
tree[rt].lz2 = 0;
}
}
void build(int rt, int l, int r) {
tree[rt].lz1 = 1, tree[rt].lz2 = 0;
if (l==r) {
cin >> tree[rt].val;
return;
}
int mid = (l+r)>>1;
build(rt<<1, l, mid);
build(rt<<1|1, mid+1, r);
push_up(rt);
}
void update(int rt, int l, int r, int L, int R, ll mul, ll add) {
if (l>=L && r<=R) {
tree[rt].val = (tree[rt].val*mul%p+(r-l+1)*add)%p;
tree[rt].lz1 = tree[rt].lz1*mul%p;
tree[rt].lz2 = (tree[rt].lz2*mul%p+add)%p;
return;
}
push_down(rt, l, r);
int mid = (l+r)>>1;
if (L<=mid) update(rt<<1, l, mid, L, R, mul, add);
if (R>mid) update(rt<<1|1, mid+1, r, L, R, mul, add);
push_up(rt);
}
ll ask(int rt, int l, int r, int L, int R) {
if (l>=L && r<=R) return tree[rt].val;
push_down(rt, l, r);
int mid = (l+r)>>1;
ll sum = 0;
if (L<=mid) sum = (sum+ask(rt<<1, l, mid, L, R))%p;
if (R>mid) sum = (sum+ask(rt<<1|1, mid+1, r, L, R))%p;
return sum;
}
int main() {
IOS;
int n; cin >> n >> p;
build(1, 1, n);
int m; cin >> m;
while(m--) {
int num; ll t, g, c;
cin >> num;
if (num==1) {
cin >> t >> g >> c;
update(1, 1, n, t, g, c, 0);
}
else if (num==2) {
cin >> t >> g >> c;
update(1, 1, n, t, g, 1, c);
}
else {
cin >> t >> g;
cout << ask(1, 1, n, t, g) << endl;
}
}
return 0;
}
区间合并
HDU 1540 环形最大子段和
const int maxn = 1e5+10;
struct Tree {
int l, r, len, pre, post;
} tree[maxn<<2];
int n, m;
inline void push_down(int rt) {
tree[rt].pre = tree[rt<<1].pre;
tree[rt].post = tree[rt<<1|1].post;
if (tree[rt<<1].pre==tree[rt<<1].len) tree[rt].pre = tree[rt<<1].pre+tree[rt<<1|1].pre;
if (tree[rt<<1|1].post==tree[rt<<1|1].len) tree[rt].post = tree[rt<<1|1].post+tree[rt<<1].post;
}
void build(int rt, int l, int r) {
tree[rt].l = l, tree[rt].r = r, tree[rt].len = r-l+1;
if (l==r) {
tree[rt].pre = tree[rt].post = 1;
return;
}
int mid = (l+r)>>1;
build(rt<<1, l, mid);
build(rt<<1|1, mid+1, r);
push_down(rt);
}
void update(int rt, int pos, int val) {
if (tree[rt].l==tree[rt].r) {
tree[rt].post = tree[rt].pre = val;
return;
}
int mid = (tree[rt].l+tree[rt].r)>>1;
if (mid>=pos) update(rt<<1, pos, val);
else update(rt<<1|1, pos, val);
push_down(rt);
}
int quary(int rt, int pos) {
if (tree[rt].l==tree[rt].r) return tree[rt].pre;
int mid = (tree[rt].l+tree[rt].r)>>1;
if (mid>=pos) {
if (tree[rt<<1].post+pos>mid) return tree[rt<<1].post+tree[rt<<1|1].pre;
else return quary(rt<<1, pos);
}
else {
if (tree[rt<<1|1].pre+mid>=pos) return tree[rt<<1|1].pre+tree[rt<<1].post;
else return quary(rt<<1|1, pos);
}
}
int main() {
while(cin >> n >> m) {
stack<int> sk;
build(1, 1, n);
for (int i = 1; i<=m; ++i) {
char ch[5]; scanf("%s", ch);
if (ch[0]=='D') {
int num; scanf("%d", &num);
update(1, num, 0); sk.push(num);
}
else if (ch[0]=='Q') {
int num; scanf("%d", &num);
printf("%d\n", quary(1, num));
}
else if (!sk.empty()) update(1, sk.top(), 1), sk.pop();
}
}
return 0;
}
线段树维护树换根之后的子树信息
CodeForces - 916E
给你一棵以1为根的树,有三种操作:
1:把树的根改为v。
2:找到包含u和v的最小子树,给他们都加上x。
3:查询以v为根的子树的总和。
首先先考虑第3个操作,固定1号点为根,记录一下当前的根是哪个点,询问时,如果询问的是新根,就是整棵子树的值。如果询问的点v在当前根的子树里,或者和当前的根没有父子关系,那么要查询的这个子树还是原来1号点为根的子树。如果询问的点v是当前根的祖先,那么由于从1号点换到了别的根,新根的祖先节点就变成了儿子节点,父子关系颠倒了。查询的其实是所有节点中除了以v点与当前根所在链上的直接儿子为根的子树以外的点。
第2个操作,先求出两个点与新根的lca,如果两个lca相同,就看lca(u,v)和新根的关系,如果不同,就取深度最大的那个lca(如果在子树内,lca为新根,否则在父子关系颠倒的子树上,所以取深度最大的)。然后就变成了判断一个点与新根的关系,与操作3类似。
const int maxn = 2e5+10;
vector<int> e[maxn];
int n, m, val[maxn], dep[maxn], f[maxn][21];
int tim, idx[maxn], rev[maxn], son[maxn], sz[maxn];
void dfs1(int u, int p) {
sz[u] = 1;
for (auto v : e[u]) {
if (v==p) continue;
dep[v] = dep[u]+1;
f[v][0] = u;
for (int i = 1; i<21; ++i) f[v][i] = f[f[v][i-1]][i-1];
dfs1(v, u);
sz[u] += sz[v];
if (sz[v]>sz[son[u]]) son[u] = v;
}
}
int top[maxn];
void dfs2(int u, int t) {
top[u] = t; idx[u] = ++tim, rev[tim] = u;
if (!son[u]) return;
dfs2(son[u], t);
for (auto v : e[u]) {
if (v==son[u] || v==f[u][0]) continue;
dfs2(v, v);
}
}
int root = 1;
int lca(int u, int v) {
if (dep[u]<dep[v]) swap(u, v);
for (int i = 19; i>=0; --i)
if (dep[f[u][i]]>=dep[v]) u = f[u][i];
if (u==v) return u;
for (int i = 19; i>=0; --i)
if (f[u][i]!=f[v][i]) u = f[u][i], v = f[v][i];
return f[u][0];
}
int get_lca(int u, int v) {
int lu = lca(root, u);
int lv = lca(root, v);
if (lu==lv) return lca(u, v);
else return dep[lu]>dep[lv] ? lu:lv;
}
ll tr[maxn<<2], lz[maxn<<2];
inline void push_up(int rt) {
tr[rt] = tr[rt<<1]+tr[rt<<1|1];
}
inline void push_down(int rt, int len) {
if (lz[rt]) {
tr[rt<<1] += 1LL*(len+1)/2*lz[rt];
tr[rt<<1|1] += 1LL*(len/2)*lz[rt];
lz[rt<<1] += lz[rt];
lz[rt<<1|1] += lz[rt];
lz[rt] = 0;
}
}
void build(int rt, int l, int r) {
if (l==r) {
tr[rt] = val[rev[l]];
return;
}
int mid = (l+r)>>1;
build(rt<<1, l, mid);
build(rt<<1|1, mid+1, r);
push_up(rt);
}
void update(int rt, int l, int r, int L, int R, int V) {
if (l>=L && r<=R) {
tr[rt] += 1LL*(r-l+1)*V;
lz[rt] += V;
return;
}
int mid = (l+r)>>1;
push_down(rt, r-l+1);
if (L<=mid) update(rt<<1, l, mid, L, R, V);
if (R>mid) update(rt<<1|1, mid+1, r, L, R, V);
push_up(rt);
}
ll query(int rt, int l, int r, int L, int R) {
if (l>=L && r<=R) return tr[rt];
int mid = (l+r)>>1; ll sum = 0;
push_down(rt, r-l+1);
if (L<=mid) sum += query(rt<<1, l, mid, L, R);
if (R>mid) sum += query(rt<<1|1, mid+1, r, L, R);
return sum;
}
void change(int x, int V) {
if (x==root) update(1, 1, n, 1, n, V);
else if (lca(root, x)!=x) update(1, 1, n, idx[x], idx[x]+sz[x]-1, V);
else {
int y = root;
for (int i = 20; i>=0; --i)
if (dep[f[y][i]]>=dep[x]+1) y = f[y][i];
if (1<=idx[y]-1) update(1, 1, n, 1, idx[y]-1, V);
if (n>=idx[y]+sz[y]) update(1, 1, n, idx[y]+sz[y], n, V);
}
}
ll ask(int x) {
if (x==root) return tr[1];
if (lca(root, x)!=x) return query(1, 1, n, idx[x], idx[x]+sz[x]-1);
int y = root;
for (int i = 20; i>=0; --i)
if (dep[f[y][i]]>=dep[x]+1) y = f[y][i];
ll sum = 0;
if (1<=idx[y]-1) sum += query(1, 1, n, 1, idx[y]-1);
if (n>=idx[y]+sz[y]) sum += query(1, 1, n, idx[y]+sz[y], n);
return sum;
}
int main() {
IOS;
cin >> n >> m;
for (int i = 1; i<=n; ++i) cin >> val[i];
for (int i = 1, a, b; i<n; ++i) {
cin >> a >> b;
e[a].push_back(b);
e[b].push_back(a);
}
dep[1] = 1;
dfs1(1, 0);
dfs2(1, 1);
build(1, 1, n);
while(m--) {
int op; cin >> op;
if (op==1) cin >> root;
else if (op==2) {
int x, y, v; cin >> x >> y >> v;
change(get_lca(x, y), v);
}
else {
int x; cin >> x;
cout << ask(x) << endl;
}
}
return 0;
}
线段树合并
bzoj3307 N个点,形成一个树状结构。有M次发放,每次选择两个点x,y, 对于x到y的路径上(含x,y)每个点发一袋Z类型的物品。完成所有发放后,每个点存放最多的是哪种物品,树上差分+线段树合并。
const int maxn = 1e5+10;
int n, m;
vector<int> e[maxn];
int x[maxn], y[maxn], z[maxn];
vector<int> vec;
struct Node {
int l, r, num, sum;
} tr[maxn*50];
int rt[maxn], idx;
inline void push_up(int now) {
auto ls = tr[tr[now].l], rs = tr[tr[now].r];
if (ls.sum>rs.sum) {
tr[now].num = ls.num;
tr[now].sum = ls.sum;
}
else if (ls.sum<rs.sum) {
tr[now].num = rs.num;
tr[now].sum = rs.sum;
}
else {
tr[now].num = min(ls.num, rs.num);
tr[now].sum = ls.sum;
}
}
void insert(int &now, int l, int r, int pos, int v) {
if (!now) now = ++idx;
if (l==r) {
tr[now].num = vec[pos-1];
tr[now].sum += v;
return;
}
int mid = (l+r)>>1;
if (pos<=mid) insert(tr[now].l, l, mid, pos, v);
else insert(tr[now].r, mid+1, r, pos, v);
push_up(now);
}
int merge(int a, int b, int l, int r) {
if (!a || !b) return a|b;
if (l==r) {
tr[a].sum += tr[b].sum;
return a;
}
int mid = (l+r)>>1;
tr[a].l = merge(tr[a].l, tr[b].l, l, mid);
tr[a].r = merge(tr[a].r, tr[b].r, mid+1, r);
push_up(a);
return a;
}
int dep[maxn], f[maxn][20];
void dfs(int u, int p) {
for (auto v : e[u]) {
if (v==p) continue;
dep[v] = dep[u]+1;
f[v][0] = u;
for (int i = 1; i<20; ++i) f[v][i] = f[f[v][i-1]][i-1];
dfs(v, u);
}
}
int lca(int a, int b) {
if (dep[a]<dep[b]) swap(a, b);
for (int i = 19; i>=0; --i)
if (dep[f[a][i]]>=dep[b]) a = f[a][i];
if (a==b) return a;
for (int i = 19; i>=0; --i)
if (f[a][i]!=f[b][i]) a = f[a][i], b = f[b][i];
return f[a][0];
}
int ans[maxn];
void dfs2(int u, int p) {
for (auto v : e[u]) {
if (v==p) continue;
dfs2(v, u);
merge(rt[u], rt[v], 1, maxn);
}
ans[u] = tr[rt[u]].num;
if (tr[rt[u]].sum<0) ans[u] = 0;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1, a, b; i<n; ++i) {
scanf("%d%d", &a, &b);
e[a].push_back(b);
e[b].push_back(a);
}
for (int i = 1; i<=m; ++i) {
scanf("%d%d%d", &x[i], &y[i], &z[i]);
vec.push_back(z[i]);
}
sort(vec.begin(), vec.end());
vec.erase(unique(vec.begin(), vec.end()), vec.end());
for (int i = 1; i<=m; ++i) z[i] = lower_bound(vec.begin(), vec.end(), z[i])-vec.begin()+1;
dep[1] = 1; dfs(1, 0);
for (int i = 1; i<=n; ++i) rt[i] = i;
idx = n;
for (int i = 1; i<=m; ++i) {
int a = x[i], b = y[i];
insert(rt[a], 1, maxn, z[i], 1);
insert(rt[b], 1, maxn, z[i], 1);
int la = lca(a, b);
insert(rt[la], 1, maxn, z[i], -1);
if (f[la][0]) insert(rt[f[la][0]], 1, maxn, z[i], -1);
}
dfs2(1, 0);
for (int i = 1; i<=n; ++i) printf("%d\n", ans[i]);
return 0;
}
扫描线
/*用线段树维护从左到右扫描到当前矩形时当前横坐标为x时y轴上的投影长度
因为对于一个矩形的两条边来说左边加1和右边减1是成对出现的,且只询问整个区间不交叉,所以不需要pushdown*/
const int maxn = 2e5+10;
struct Seg {
double x, y1, y2; int k;
} seg[maxn];
int n, tot;
double arr[maxn];
int fd(double x) {
return lower_bound(arr+1, arr+tot+1, x)-arr;
}
struct Node {
double len;
int lz;
} tree[maxn<<2];
void build(int rt, int l, int r) {
tree[rt] = {0, 0};
if (l==r) return;
int mid = (l+r)>>1;
build(rt<<1, l, mid);
build(rt<<1|1, mid+1, r);
}
inline void push_up(int rt, int l, int r) {
if (tree[rt].lz) tree[rt].len = arr[r+1]-arr[l];
else tree[rt].len = tree[rt<<1].len+tree[rt<<1|1].len;
}
void update(int rt, int l, int r, int L, int R, int k) {
if (l>=L && r<=R) {
tree[rt].lz += k;
push_up(rt, l, r);
return;
}
int mid = (l+r)>>1;
if (L<=mid) update(rt<<1, l, mid, L, R, k);
if (R>mid) update(rt<<1|1, mid+1, r, L, R, k);
push_up(rt, l, r);
}
int main() {
IOS;
int k = 0;
while(cin >> n && n) {
tot = 0;
build(1, 1, 100000);
for (int i = 1; i<=n; ++i) {
double a, b, c, d;
cin >> a >> b >> c >> d;
seg[2*i-1] = {b, a, c, 1};
seg[2*i] = {d, a, c, -1};
arr[++tot] = a;
arr[++tot] = c;
}
sort(arr+1, arr+tot+1, [](double t1, double t2) {return t1<t2;});
tot = unique(arr+1, arr+tot+1)-arr-1;
sort(seg+1, seg+2*n+1, [](Seg a, Seg b) {return a.x<b.x;});
double ans = 0;
for (int i = 1; i<=2*n; ++i) {
ans += tree[1].len*(seg[i].x-seg[i-1].x);
update(1, 1, 100000, fd(seg[i].y1), fd(seg[i].y2)-1, seg[i].k);
}
cout << "Test case #" << ++k << endl;
cout << fixed << setprecision(2) << "Total explored area: " << ans << endl << endl;
}
return 0;
}
主席树
求区间第k大
POJ 2104 K-th Number 求区间内第k小的数字
const int maxn = 2e5+10;
struct NODE {
int l, r, sum;
} hjt[maxn<<5];
int n, n2, m, tot, a[maxn], b[maxn], root[maxn];
int getid(int x) {
return lower_bound(b+1, b+n2, x)-b;
}
void insert(int l, int r, int pre, int &now, int p) {
hjt[++tot] = hjt[pre];
now = tot; hjt[now].sum++;
if (l==r) return;
int mid = (l+r)>>1;
if (p<=mid) insert(l, mid, hjt[pre].l, hjt[now].l, p);
else insert(mid+1, r, hjt[pre].r, hjt[now].r, p);
}
int query(int l, int r, int pre, int now, int p) {
if (l==r) return l;
int mid = (l+r)>>1;
int tmp = hjt[hjt[now].l].sum-hjt[hjt[pre].l].sum;
if (p<=tmp) return query(l, mid, hjt[pre].l, hjt[now].l, p);
else return query(mid+1, r, hjt[pre].r, hjt[now].r, p-tmp);
}
int main() {
cin >> n >> m;
for (int i = 1; i<=n; ++i) scanf("%d", &a[i]), b[i] = a[i];
sort(b+1, b+n+1);
n2 = unique(b+1, b+n+1)-b;
for (int i = 1; i<=n; ++i) insert(1, n, root[i-1], root[i], getid(a[i]));
int l, r, k;
while(m--) {
scanf("%d%d%d", &l, &r, &k);
printf("%d\n", b[query(1, n, root[l-1], root[r], k)]);
}
return 0;
}
求区间不同数的个数
SPOJ - DQUERY
const int maxn = 1e5+10;
struct NODE {
int l, r, sum;
} hjt[maxn<<5];
int n, n2, m, tot, a[maxn], root[maxn], last[maxn*10];
void insert(int l, int r, int pre, int &now, int p, int v) {
hjt[++tot] = hjt[pre];
now = tot; hjt[tot].sum+=v;
if (l==r) return;
int mid = (l+r)>>1;
if (p<=mid) insert(l, mid, hjt[pre].l, hjt[now].l, p, v);
else insert(mid+1, r, hjt[pre].r, hjt[now].r, p, v);
}
int query(int l, int r, int now, int L, int R) {
if (l>=L && r<=R) return hjt[now].sum;
int mid = (l+r)>>1, sum = 0;
if (L<=mid) sum += query(l, mid, hjt[now].l, L, R);
if (R>mid) sum += query(mid+1, r, hjt[now].r, L, R);
return sum;
}
int main() {
cin >> n;
for (int i = 1; i<=n; ++i) scanf("%d", &a[i]);
for (int i = 1; i<=n; ++i) {
insert(1, n, root[i-1], root[i], i, 1);
if (last[a[i]]) insert(1, n, root[i], root[i], last[a[i]], -1);
last[a[i]] = i;
}
cin >> m;
for (int i = 1, l, r; i<=m; ++i) {
scanf("%d%d", &l, &r);
printf("%d\n", query(1, n, root[r], l, r));
}
return 0;
}
区间修改(标记永久化)
HDU4348 To the moon 区间修改+求历史区间和
const int maxn = 2e5+10;
const int maxm = 2e6+10;
struct Node {
int l, r, lz; ll sum;
} node[maxn*40];
int n, m, tot, root[maxn];
void build(int l, int r, int &now) {
now = ++tot;
if (l==r) {
scanf("%lld", &node[now].sum);
return;
}
int mid = (l+r)>>1;
build(l, mid, node[now].l);
build(mid+1, r, node[now].r);
node[now].sum = node[node[now].l].sum+node[node[now].r].sum;
}
void update(int l, int r, int pre, int &now, int L, int R, int V) {
node[++tot] = node[pre];
now = tot;
node[now].sum += 1LL*(R-L+1)*V;
if (l==L && r==R) {
node[now].lz += V; return;
}
int mid = (l+r)>>1;
if (R<=mid) update(l, mid, node[pre].l, node[now].l, L, R, V);
else if (L>mid) update(mid+1, r, node[pre].r, node[now].r, L, R, V);
else {
update(l, mid, node[pre].l, node[now].l, L, mid, V);
update(mid+1, r, node[pre].r, node[now].r, mid+1, R, V);
}
}
ll query(int l, int r, int now, int L, int R) {
if (l>=L && r<=R) return node[now].sum;
int mid = (l+r)>>1;
ll sum = (R-L+1)*node[now].lz;
if (R<=mid) sum += query(l, mid, node[now].l, L, R);
else if (L>mid) sum += query(mid+1, r, node[now].r, L, R);
else {
sum += query(l, mid, node[now].l, L, mid);
sum += query(mid+1, r, node[now].r, mid+1, R);
}
return sum;
}
int main() {
int f = 0;
while(cin >> n >> m) {
if (f) putchar(endl);
f = 1;
int time = 1; tot = 0;
build(1, n, root[time]);
char op[5]; int l, r, d;
while(m--) {
scanf("%s", op);
if (op[0]=='Q') {
scanf("%d%d", &l, &r);
printf("%lld\n", query(1, n, root[time], l, r));
}
else if (op[0]=='H') {
scanf("%d%d%d", &l, &r, &d);
printf("%lld\n", query(1, n, root[d+1], l, r));
}
else if (op[0]=='C') {
scanf("%d%d%d", &l, &r, &d);
update(1, n, root[time], root[time+1], l, r, d);
++time;
}
else scanf("%d", &time), ++time;
}
for (int i = 0; i<=tot; ++i) node[i].l = node[i].r = node[i].sum = 0;
}
return 0;
}
树状数组
HDU 5869 区间GCD
const int maxn = 1e5+10;
int n, m, arr[maxn], pre[maxn], last[maxn*10];
ll c[maxn], ans[maxn];
void add(int x, int y) {
while(x<=n) c[x] += y, x += x&-x;
}
ll ask(int x) {
ll sum = 0;
while(x) sum += c[x], x -= x&-x;
return sum;
}
vector<P> q[maxn];
int main(void) {
while(cin >> n >> m) {
for (int i = 1; i<=n; ++i) {
scanf("%d", &arr[i]);
pre[i] = arr[i]==arr[i-1] ? pre[i-1]:i-1;
}
for (int i = 1, l, r; i<=m; ++i) {
scanf("%d%d", &l, &r);
q[r].push_back({i, l});
}
for (int i = 1; i<=n; ++i) {
for (int j = i, x = arr[j]; j; j = pre[j], x = __gcd(x, arr[j])) {
if (j>last[x]) {
if (last[x]) add(last[x], -1);
add(j, 1);
last[x] = j;
}
if (x==1) break;
}
for (auto v : q[i]) ans[v.first] = ask(i)-ask(v.second-1);
}
for (int i = 1; i<=m; ++i) printf("%lld\n", ans[i]);
for (int i = 1; i<=n; ++i) q[i].clear();
clr(last, 0); clr(c, 0);
}
return 0;
}
二维区间01翻转 POJ 2155
const int maxn = 1e3+10;
int n, m, flag, c[maxn][maxn];
void add(int x, int y) {
for (int i = x; i<=n; i+=i&-i)
for (int j = y; j<=n; j+=j&-j)
c[i][j] += 1;
}
int ask(int x, int y) {
int sum = 0;
for (int i = x; i; i-=i&-i)
for (int j = y; j; j-=j&-j)
sum += c[i][j];
return sum;
}
int main(void) {
int T; cin >> T;
while(T--) {
clr(c, 0);
if (flag) putchar(endl);
cin >> n >> m;
int a, b, c, d;
while(m--) {
char ch[10];
scanf("%s", ch);
if (ch[0]=='C') {
scanf("%d%d%d%d", &a, &b, &c, &d);
add(a, b); add(a, d+1); add(c+1, b); add(c+1, d+1);
}
else {
scanf("%d%d", &a, &b);
printf("%d\n", ask(a, b)%2);
}
}
flag = 1;
}
return 0;
}
CodeForces - 1354D 树状数组倍增找第k大,输入正数表示插入,负数表示删除第k个数,保证删除的数字存在。
const int maxn = 1<<20;
const int maxm = 2e5+10;
int n, q, c[maxn+1];
void add(int x, int y) {
while(x<maxn) {
c[x] += y;
x += x&-x;
}
}
int get_k(int x) {
int res = 0;
for (int i = maxn/2; i>=1; i>>=1)
if (c[res+i]<x) {
res += i;
x -= c[res];
}
return res+1;
}
int main(void) {
IOS;
cin >> n >> q;
for (int i = 1; i<=n; ++i) {
int num; cin >> num;
add(num, 1);
}
while(q--) {
int num; cin >> num;
if (num>0) add(num, 1);
else {
num = -num;
int x = get_k(num);
add(x, -1);
}
}
int ans = 0;
for (int i = 1; i<maxn; ++i)
if (c[i]) {
ans = i;
break;
}
cout << ans << endl;
return 0;
}
HDU - 6534 树状数组+莫队 询问区间[l,r]中满足相邻两个数大小不超过k的数对,如果一个一个加入数字的话,设当前数字为i,那么对答案的贡献就是之前的数字之中[ai−k,ai+k]范围内的数字的数量,可以用莫队来维护l,r,然后每次的修改和查询操作用树状数组来操作。
const int maxn = 1e5+10;
const int maxm = 1e6+10;
int n, nn, m, k;
int a[maxn], b[maxn], p[maxn];
int find(int x) {
return lower_bound(b+1, b+nn+1, x)-b;
}
int find2(int x) {
return upper_bound(b+1, b+nn+1, x)-b;
}
int c[maxn];
void insert(int x, int y) {
while(x<=n) {
c[x] += y;
x += x&-x;
}
}
int ask(int x) {
int sum = 0;
while(x) {
sum += c[x];
x -= x&-x;
}
return sum;
}
struct Q {
int l, r, i;
} q[maxn];
int l = 1, r = 0;
int ans[maxn], res, up[maxn], low[maxn];
void add(int x) {
res += ask(up[x])-ask(low[x]-1);
insert(a[x], 1);
}
void sub(int x) {
insert(a[x], -1);
res -= ask(up[x])-ask(low[x]-1);
}
int main() {
IOS;
cin >> n >> m >> k;
for (int i = 1; i<=n; ++i) cin >> a[i], b[i] = a[i];
sort(b+1, b+n+1);
nn = unique(b+1, b+n+1)-b-1;
for (int i = 1; i<=n; ++i) {
low[i] = find(a[i]-k);
up[i] = find2(a[i]+k)-1;
a[i] = find(a[i]);
}
for (int i = 1; i<=m; ++i) {
cin >> q[i].l >> q[i].r;
q[i].i = i;
}
int sz = sqrt(m)+1;
sort(q+1, q+m+1, [=](Q x, Q y) {return (x.l/sz^y.l/sz) ? x.l/sz<y.l/sz : ((x.l/sz)%2 ? x.r<y.r:x.r>y.r);});
for (int i = 1; i<=m; ++i) {
while(q[i].r > r) add(++r);
while(q[i].l > l) sub(l++);
while(q[i].r < r) sub(r--);
while(q[i].l < l) add(--l);
ans[q[i].i] = res;
}
for (int i = 1; i<=m; ++i) cout << ans[i] << endl;
return 0;
}
树套树
树状数组套字典树
求区间[l,r]中所有满足\(x\ xor\ a < b\)的不同的数的个数,求区间不同的数可以用树状数组离线来做,求满足\(x xor a < b\)的数可以用字典树来做,树状数组的每一个节点开一个字典树即可。
const int maxn = 1e5+10;
const int maxm = maxn*400;
int n, m, a[maxn];
int tr[maxm][2], cnt[maxm], idx;
int c[maxn], rt[maxn], lst[maxn], ans[maxn];
struct INFO {
int l, a, b, i;
};
vector<INFO> q[maxn];
void insert(int &p, int v, int x) {
if (!p) p = ++idx;
int now = p;
for (int i = 20; i>=0; --i) {
int t = x>>i&1;
if (!tr[now][t]) tr[now][t] = ++idx;
now = tr[now][t];
cnt[now] += v;
}
}
void add(int x, int v, int y) {
while(x<=n) {
insert(rt[x], v, y);
x += x&-x;
}
}
int query(int p, int a, int b) {
int sum = 0;
for (int i = 20; i>=0; --i) {
int t = a>>i&1;
if (b>>i&1) {
sum += cnt[tr[p][t]];
p = tr[p][t^1];
}
else p = tr[p][t];
if (!p) break;
}
return sum+cnt[p];
}
int ask(int x, int a, int b) {
int sum = 0;
while(x) {
sum += query(rt[x], a, b);
x -= x&-x;
}
return sum;
}
int main() {
IOS;
cin >> n;
for (int i = 1; i<=n; ++i) cin >> a[i];
cin >> m;
for (int i = 1; i<=m; ++i) {
int l, r, c, d; cin >> l >> r >> c >> d;
q[r].push_back({l, c, d, i});
}
for (int i = 1; i<=n; ++i) {
if (lst[a[i]]) add(lst[a[i]], -1, a[i]);
add(i, 1, a[i]);
lst[a[i]] = i;
for (auto v : q[i]) ans[v.i] = ask(i, v.a, v.b)-ask(v.l-1, v.a, v.b);
}
for (int i = 1; i<=m; ++i) cout << ans[i] << endl;
return 0;
}
线段树套splay
AcWing 2476 查询区间排名,区间排名为k的值,查询前驱后继,修改某个位置的值
const int maxn = 1e5+10;
int n, m, a[maxn];
struct Node {
int s[2], v, sz, p;
void init(int _v, int _p) {
v = _v, p = _p;
sz = 1;
}
} tr[maxn*200];
int idx, rts[maxn*200];
inline void push_up(int u) {
tr[u].sz = tr[tr[u].s[0]].sz+tr[tr[u].s[1]].sz+1;
}
inline void rotate(int x) {
int y = tr[x].p, z = tr[y].p;
int k = tr[y].s[1] == x;
tr[z].s[tr[z].s[1]==y] = x, tr[x].p = z;
tr[y].s[k] = tr[x].s[k^1], tr[tr[x].s[k^1]].p = y;
tr[x].s[k^1] = y, tr[y].p = x;
push_up(y), push_up(x);
}
void splay(int &rt, int x, int k) {
while(tr[x].p!=k) {
int y = tr[x].p, z = tr[y].p;
if (z!=k)
if ((tr[y].s[1]==x)^(tr[z].s[1]==y)) rotate(x);
else rotate(y);
rotate(x);
}
if (!k) rt = x;
}
void insert(int &rt, int v) {
int u = rt, p = 0;
while(u) p = u, u = tr[u].s[v>tr[u].v];
u = ++idx;
if (p) tr[p].s[v>tr[p].v] = u;
tr[u].init(v, p);
splay(rt, u, 0);
}
void change(int &rt, int pre, int now) {
int u = rt;
//因为要保证有序性,所以不能直接修改原来的值,应该先删除再插入
while(u) {
if (pre>tr[u].v) u = tr[u].s[1];
else if (pre==tr[u].v) break;
else u = tr[u].s[0];
}
splay(rt, u, 0);
int l = tr[u].s[0], r = tr[u].s[1];
//找到原来的数的前驱和后继,后缀的左儿子就是要删的数
while(tr[l].s[1]) l = tr[l].s[1];
while(tr[r].s[0]) r = tr[r].s[0];
splay(rt, l, 0), splay(rt, r, l);
tr[r].s[0] = 0;
push_up(r), push_up(l);
insert(rt, now);
}
int get_rank(int rt, int x) {
int u = rt, sum = 0; //查询所有小于x的数的数量,+1即是排名
while(u) {
if (x>tr[u].v) {
sum += tr[tr[u].s[0]].sz+1;
u = tr[u].s[1];
}
else u = tr[u].s[0];
}
return sum;
}
int get_pre(int rt, int x) {
int u = rt, maxx = -1;
while(u) {
if (x>tr[u].v) {
maxx = max(maxx, tr[u].v);
u = tr[u].s[1];
}
else u = tr[u].s[0];
}
return maxx;
}
int get_suc(int rt, int x) {
int u = rt, minn = INF;
while(u) {
if (x<tr[u].v) {
minn = min(minn, tr[u].v);
u = tr[u].s[0];
}
else u = tr[u].s[1];
}
return minn;
}
void build(int rt, int l, int r) {
insert(rts[rt], -INF);
insert(rts[rt], INF);
for (int i = l; i<=r; ++i) insert(rts[rt], a[i]);
if (l==r) return;
int mid = (l+r)>>1;
build(rt<<1, l, mid);
build(rt<<1|1, mid+1, r);
}
void update(int rt, int l, int r, int pos, int p, int q) {
change(rts[rt], p, q);
if (l==r) return;
int mid = (l+r)>>1;
if (pos<=mid) update(rt<<1, l, mid, pos, p, q);
else update(rt<<1|1, mid+1, r, pos, p, q);
}
int query_rank(int rt, int l, int r, int L, int R, int x) {
if (l>=L && r<=R) return get_rank(rts[rt], x)-1;
int mid = (l+r)>>1, sum = 0;
if (L<=mid) sum += query_rank(rt<<1, l, mid, L, R, x);
if (R>mid) sum += query_rank(rt<<1|1, mid+1, r, L, R, x);
return sum;
}
int query_pre(int rt, int l, int r, int L, int R, int x) {
if (l>=L && r<=R) return get_pre(rts[rt], x);
int mid = (l+r)>>1, maxx = -1;
if (L<=mid) maxx = max(maxx, query_pre(rt<<1, l, mid, L, R, x));
if (R>mid) maxx = max(maxx, query_pre(rt<<1|1, mid+1, r, L, R, x));
return maxx;
}
int query_suc(int rt, int l, int r, int L, int R, int x) {
if (l>=L && r<=R) return get_suc(rts[rt], x);
int mid = (l+r)>>1, minn = INF;
if (L<=mid) minn = min(minn, query_suc(rt<<1, l, mid, L, R, x));
if (R>mid) minn = min(minn, query_suc(rt<<1|1, mid+1, r, L, R, x));
return minn;
}
int main() {
IOS;
cin >> n >> m;
for (int i = 1; i<=n; ++i) cin >> a[i];
build(1, 1, n);
int op, l, r, x;
while(m--) {
cin >> op >> l >> r;
if (op==1) {
//查询排名(从小到大数是第几个,相同看第一个)
cin >> x;
cout << query_rank(1, 1, n, l, r, x)+1 << endl;
}
else if (op==2) {
cin >> x; //查询排名的值
int ll = 0, rr = 1e8+10;
while(ll<rr) {
int mid = (ll+rr+1)>>1;
if (query_rank(1, 1, n, l, r, mid)+1<=x) ll = mid;
else rr = mid-1;
}
// while(ll<rr) {
// int mid = (ll+rr)>>1;
// if (query_rank(1, 1, n, l, r, mid)+1>=x) rr = mid;
// else ll = mid+1;
// }
cout << ll << endl;
}
else if (op==3) {
//修改某个位置上的数
update(1, 1, n, l, a[l], r);
a[l] = r; //一定要跟新一下原来的数
}
else if (op==4) {
cin >> x; //查询前驱
cout << query_pre(1, 1, n, l, r, x) << endl;
}
else if (op==5) {
cin >> x; //查询后继
cout << query_suc(1, 1, n, l, r, x) << endl;
}
}
return 0;
}
点分治
POJ 1741 Tree 计算距离小于k的不同点对个数
const int maxn = 2e5+10;
int n, m, rt, tot, tota; ll ans;
bool vis[maxn];
int d[maxn], sz[maxn], a[maxn], b[maxn], h[maxn], cnt[maxn], mx[maxn];
struct E {
int to, w, nxt;
} e[maxn<<1];
void add(int u, int v, int w) {
e[++tot] = {v, w, h[u]};
h[u] = tot;
}
void init() {
ans = tot = 0;
for (int i = 0; i<=n; ++i) h[i] = 0, vis[i] = 0;
}
void getrt(int u, int p, int szr) { //szr存当前的子树中的节点个数
sz[u] = 1; mx[u] = 0;
for (int i = h[u]; i; i=e[i].nxt) {
int v = e[i].to;
if (v==p || vis[v]) continue;
getrt(v, u, szr);
sz[u] += sz[v];
if (sz[v]>mx[u]) mx[u] = sz[v];
}
if (szr-sz[u]>mx[u]) mx[u] = szr-sz[u];
if (!rt || mx[u]<mx[rt]) rt = u;
}
void update(int u, int p) {
sz[u] = 1;
for (int i = h[u]; i; i=e[i].nxt) {
int v = e[i].to;
if (v==p || vis[v]) continue;
update(v, u);
sz[u] += sz[v];
}
}
void getdis(int u, int p, int x) {
b[u] = x, ++cnt[x], a[++tota] = u;
for (int i = h[u]; i; i=e[i].nxt) {
int v = e[i].to, w = e[i].w;
if (v==p || vis[v]) continue;
d[v] = d[u]+w;
getdis(v, u, x);
}
}
bool cmp(int a, int b) {
return d[a]<d[b];
}
void calc(int u) {
d[u] = tota = 0;
b[u] = u, ++cnt[u], a[++tota] = u; //存下每个点为根的子树大小
for (int i = h[u]; i; i=e[i].nxt) {
int v = e[i].to, w = e[i].w;
if (vis[v]) continue;
d[v] = d[u]+w;
getdis(v, u, v);
}
//cout << tota << endl;
sort(a+1, a+tota+1, cmp);
int l = 1, r = tota; --cnt[b[a[l]]];
//cout << l << ' ' << r << endl;
while(l<r) {
while(r>l && d[a[l]]+d[a[r]]>m) --cnt[b[a[r]]], --r; //cnt存储l+1 ~ r之间同一子树的点数
if (l>=r) break;
ans += r-l-cnt[b[a[l]]]; //计算时减去与a[l]同一子树的贡献
//cout << ans << endl;
++l;
--cnt[b[a[l]]];
}
for (int i = 0; i<=tota; ++i) b[a[i]] = cnt[a[i]] = 0;
}
void div(int u) {
vis[u] = 1;
calc(u); //计算贡献
for (int i = h[u]; i; i=e[i].nxt) {
int v = e[i].to;
if (vis[v]) continue;
rt = 0; sz[rt] = INF;
int t = sz[v];
getrt(v, -1, t);
update(rt, -1);
div(rt);
}
}
int main(void) {
while(~scanf("%d%d", &n, &m) && (n||m)) {
init();
for (int i = 1, a, b, c; i<n; ++i) {
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
add(b, a, c);
}
rt = 0, sz[rt] = INF;
getrt(1, -1, n);
update(rt, -1); //第二遍求重心保证sz是以重心为根算出来的
div(rt);
printf("%lld\n", ans);
}
return 0;
}
Gym - 102832F \(i\)和\(j\)是树上不同的两个点,计算下面公式的值
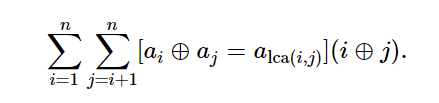
虽然题目是有根树,但是某个节点最多只有一个儿子的深度比自己小,利用这点可以处理父子关系颠倒的情况,然后拆位处理下标异或即可。
const int maxn = 2e6+10;
const int maxm = 1e6+10;
vector<int> e[maxn];
int sz[maxn], mx[maxn], cnt[maxn][20];
int rt, val[maxn], vis[maxn], tsz[maxn];
vector<int> res, tmp;
ll ans = 0;
int d[maxn];
void get_dis(int u, int p) {
for (auto v : e[u]) {
if (v==p) continue;
d[v] = d[u]+1;
get_dis(v, u);
}
}
void get_rt(int u, int p, int szr) {
sz[u] = 1, mx[u] = 0;
for (auto v : e[u]) {
if (v==p || vis[v]) continue;
get_rt(v, u, szr);
sz[u] += sz[v];
if (sz[v]>mx[u]) mx[u] = sz[u];
}
if (szr-sz[u]>mx[u]) mx[u] = szr-sz[u];
if (!rt || mx[u]<mx[rt]) rt = u;
}
void update(int u, int p) {
sz[u] = 1;
for (auto v : e[u]) {
if (v==p || vis[v]) continue;
update(v, u);
sz[u] += sz[v];
}
}
void solve1(int u, int p, int x) {
res.push_back(val[u]);
tmp.push_back(u);
for (int i = 0; i<20; ++i) {
int t = u>>i&1;
if (t) ans += (1LL<<i)*(tsz[val[u]^x]-cnt[val[u]^x][i]);
else ans += (1LL<<i)*cnt[val[u]^x][i];
}
//cout << u << ' ' << ans << endl;
for (auto v : e[u]) {
if (v==p || vis[v]) continue;
solve1(v, u, x);
}
}
void solve2(int u, int p, int x) {
int t = -1;
for (auto v : e[u]) {
if (v==p || vis[v]) continue;
if (d[v]<d[u]) {
t = v;
continue;
}
solve1(v, u, x);
}
if (t!=-1) solve2(t, u, val[t]);
}
void calc(int u) {
int t = -1;
for (auto v : e[u]) {
if (vis[v]) continue;
if (d[v]<d[u]) {
t = v;
continue;
}
solve1(v, u, val[u]);
for (auto num : tmp) {
++tsz[val[num]];
for (int i = 0; i<20; ++i)
if (num>>i&1) ++cnt[val[num]][i];
}
tmp.clear();
}
if (t!=-1) {
++tsz[val[u]];
res.push_back(val[u]);
for (int i = 0; i<20; ++i)
if (u>>i&1) {
++cnt[val[u]][i];
}
solve2(t, u, val[t]);
}
for (auto v : res)
for (int i = 0; i<20; ++i) cnt[v][i] = 0, tsz[v] = 0;
tmp.clear();
res.clear();
}
void div(int u) {
//cout << u << endl;
vis[u] = 1;
calc(u);
for (auto v : e[u]) {
if (vis[v]) continue;
rt = 0; sz[rt] = INF;
int t = sz[v];
get_rt(v, -1, t);
update(rt, -1);
div(rt);
}
}
int main() {
IOS;
int n; cin >> n;
for (int i = 1; i<=n; ++i) cin >> val[i];
for (int i = 1; i<n; ++i) {
int a, b; cin >> a >> b;
e[a].push_back(b);
e[b].push_back(a);
}
rt = 0, sz[rt] = INF;
d[1] = 1;
get_dis(1, 0);
get_rt(1, -1, n);
update(rt, -1);
div(rt);
cout << ans << endl;
return 0;
}
树链剖分
bzoj 1036 询问树上两点最大权值,权值和,修改某个点的值,树剖之后建线段树即可。
const int INF = 0x3f3f3f3f;
const int maxn = 1e5+10;
struct E {
int to, nxt;
} e[maxn<<2];
int h[maxn], tot;
void add(int u, int v) {
e[++tot] = {v, h[u]};
h[u] = tot;
}
int dep[maxn], fa[maxn], sz[maxn], son[maxn];
void dfs1(int u, int p) {
sz[u] = 1;
for (int i = h[u]; i; i=e[i].nxt) {
int v = e[i].to;
if (v==p) continue;
dep[v] = dep[u]+1;
fa[v] = u;
dfs1(v, u);
sz[u] += sz[v];
if (sz[v]>sz[son[u]]) son[u] = v;
}
}
int top[maxn], tim, id[maxn], rev[maxn];
void dfs2(int u, int t) {
top[u] = t;
id[u] = ++tim; //给结点标时间戳
rev[tim] = u; //时间戳对应的结点
if (!son[u]) return;
dfs2(son[u], t); //沿着重儿子dfs
for (int i = h[u]; i; i=e[i].nxt) {
int v = e[i].to;
if (v!=fa[u] && v!=son[u]) dfs2(v, v);
}
}
struct Node {
int mx, sum;
} tree[maxn<<2];
int n, w[maxn], maxx, sum, m;
inline void push_up(int rt) {
tree[rt].mx = max(tree[rt<<1].mx, tree[rt<<1|1].mx);
tree[rt].sum = tree[rt<<1].sum+tree[rt<<1|1].sum;
}
void build(int rt, int l, int r) {
if (l==r) {
tree[rt].mx = tree[rt].sum = w[rev[l]];
return;
}
int mid = (l+r)>>1;
build(rt<<1, l, mid);
build(rt<<1|1, mid+1, r);
push_up(rt);
}
void query(int rt, int l, int r, int L, int R) {
if (l>=L && r<=R) {
maxx = max(maxx, tree[rt].mx);
sum += tree[rt].sum;
return;
}
int mid = (l+r)>>1;
if (L<=mid) query(rt<<1, l, mid, L, R);
if (R>mid) query(rt<<1|1, mid+1, r, L, R);
}
void ask(int u, int v) {
while(top[u]!=top[v]) { //不在同一条重链上
if (dep[top[u]]<dep[top[v]]) swap(u, v);
query(1, 1, n, id[top[u]], id[u]);
u = fa[top[u]];
}
if (dep[u]>dep[v]) swap(u, v); //在一条重链上
query(1, 1, n, id[u], id[v]);
}
void update(int rt, int l, int r, int pos, int val) {
if (l==r) {
tree[rt].mx = tree[rt].sum = val;
return;
}
int mid = (l+r)>>1;
if (pos<=mid) update(rt<<1, l, mid, pos, val);
else update(rt<<1|1, mid+1, r, pos, val);
push_up(rt);
}
char str[11];
int main(void) {
cin >> n;
for (int i = 1, a, b; i<n; ++i) {
scanf("%d%d", &a, &b);
add(a, b);
add(b, a);
}
for (int i = 1; i<=n; ++i) scanf("%d", &w[i]);
dep[1] = 1;
dfs1(1, 0);
dfs2(1, 1);
build(1, 1, n);
cin >> m;
for (int i = 1, a, b; i<=m; ++i) {
scanf("%s", str);
scanf("%d%d", &a, &b);
if (str[0]=='C') update(1, 1, n, id[a], b);
else {
sum = 0;
maxx = -INF;
ask(a, b);
if (str[1]=='M') printf("%d\n", maxx);
else printf("%d\n", sum);
}
}
return 0;
}
hdu2586 树剖求lca算树上两点间距离
const int maxn = 1e5+10;
struct E {
int to, w, nxt;
} e[maxn<<2];
int h[maxn], tot;
void add(int u, int v, int w) {
e[++tot] = {v, w, h[u]};
h[u] = tot;
}
int dep[maxn], fa[maxn], sz[maxn], son[maxn], dis[maxn];
void dfs1(int u, int p) {
sz[u] = 1;
for (int i = h[u]; i; i=e[i].nxt) {
int v = e[i].to;
if (v==p) continue;
dep[v] = dep[u]+1;
dis[v] = dis[u]+e[i].w;
fa[v] = u;
dfs1(v, u);
sz[u] += sz[v];
if (sz[v]>sz[son[u]]) son[u] = v;
}
}
int top[maxn];
void dfs2(int u) {
if (u==son[fa[u]]) top[u] = top[fa[u]];
else top[u] = u;
for (int i = h[u]; i; i=e[i].nxt) {
int v = e[i].to;
if (v!=fa[u]) dfs2(v);
}
}
int lca(int u, int v) {
while(top[u]!=top[v]) { //不在同一条重链上
if (dep[top[u]]>dep[top[v]]) u = fa[top[u]]; //将顶端节点深度大的上移
else v = fa[top[v]];
}
return dep[u]>dep[v]?v:u; //返回深度小的节点
}
int n, m;
void init() {
tot = 0;
for (int i = 0; i<=n; ++i) h[i] = 0, son[i] = 0;
}
int main(void) {
int __; cin >> __;
while(__--) {
cin >> n >> m;
init();
for (int i = 1, a, b, c; i<n; ++i) {
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
add(b, a, c);
}
dfs1(1, 0);
dfs2(1);
while(m--) {
int a, b; scanf("%d%d", &a, &b);
printf("%d\n", dis[a]+dis[b]-dis[lca(a, b)]*2);
}
}
return 0;
}
HDU - 6962 给你一颗树,有两种操作。一种是给树上两个点之间的点\((x_1, x_2...x_k)\)加上\(1^2, 2^2...k^2\)。另一种是查询树上某个节点的值,初始每个节点的值都是\(0\)。
题目很明显可以树剖之后建线段树来做区间修改和单点查询。 给区间加上等差数列的平方可以用加二次函数的形式。对于区间\([l,r]\),设\(k=l-1\),可以对每个数加上\((i-k)^2\),\(i\)是这个元素的下标,但是这样不具有可加性,可以试着把式子展开,变成\(i^2-2ki+k^2\),将\(i\)提出来,变成\(i^2 \times 1 - 2i \times k + k^2\),我们发现\(1\),\(k\),\(k^2\)是可以累加的,用线段树分别维护区间内三种数的和即可。
由于树剖之后两个结点会同时往上跳,就有了要计算正着加和倒着加的情况,倒着加也很简单,设\(k\)等于\(r+1\),就变成了对每个数加\((k-i)^2\),翻转一下变成\(i-k\),发现和前面只是\(k\)的取值不同罢了。
const int maxn = 2e5+10;
const int maxm = 1e7+10;
int n, q;
vector<int> e[maxn];
int dep[maxn], fa[maxn], sz[maxn], son[maxn];
void dfs1(int u, int p) {
sz[u] = 1;
for (auto v : e[u]) {
if (v==p) continue;
dep[v] = dep[u]+1;
fa[v] = u;
dfs1(v, u);
sz[u] += sz[v];
if (sz[v]>sz[son[u]]) son[u] = v;
}
}
int top[maxn], tim, id[maxn], rev[maxn];
void dfs2(int u, int t) {
top[u] = t;
id[u] = ++tim;
rev[tim] = u;
if (!son[u]) return;
dfs2(son[u], t);
for (auto v : e[u])
if (v!=fa[u] && v!=son[u]) dfs2(v, v);
}
struct Node {
ll lz1, lz2, lz3;
} tr[maxn<<2];
inline void push_down(int rt) {
if (tr[rt].lz1) {
Node &f = tr[rt];
Node &ls = tr[rt<<1];
Node &rs = tr[rt<<1|1];
ls.lz1 += f.lz1;
ls.lz2 += f.lz2;
ls.lz3 += f.lz3;
rs.lz1 += f.lz1;
rs.lz2 += f.lz2;
rs.lz3 += f.lz3;
f.lz1 = f.lz2 = f.lz3 = 0;
}
}
void update(int rt, int l, int r, int L, int R, ll val) {
if (l>=L && r<=R) {
tr[rt].lz1 += 1;
tr[rt].lz2 += val*val;
tr[rt].lz3 += val;
return;
}
push_down(rt);
int mid = (l+r)>>1;
if (L<=mid) update(rt<<1, l, mid, L, R, val);
if (R>mid) update(rt<<1|1, mid+1, r, L, R, val);
}
Node ask(int rt, int l, int r, int pos) {
if (l==r) return tr[rt];
push_down(rt);
int mid = (l+r)>>1;
if (pos<=mid) return ask(rt<<1, l, mid, pos);
else return ask(rt<<1|1, mid+1, r, pos);
}
int lca(int u, int v) {
while(top[u]!=top[v]) {
if (dep[top[u]]>dep[top[v]]) u = fa[top[u]];
else v = fa[top[v]];
}
return dep[u]>dep[v] ? v:u;
}
void modify(int u, int v) {
int l = 1, r = dep[u]+dep[v]-2*dep[lca(u, v)]+1;
int add = 0;
while(top[u]!=top[v]) {
if (dep[top[u]]>dep[top[v]]) { //u往上跳,从top[u]到u倒着加
add = id[u]+l;
l += id[u]-id[top[u]];
update(1, 1, n, id[top[u]], id[u], add);
u = fa[top[u]];
++l;
}
else { //v往上跳从top[v]到v正着加
r -= dep[v]-dep[top[v]];
add = id[top[v]]-r;
update(1, 1, n, id[top[v]], id[v], add);
v = fa[top[v]];
--r;
}
}
if (dep[u]>dep[v]) {
add = id[u]+l;
update(1, 1, n, id[v], id[u], add);
}
else {
add = id[u]-l;
update(1, 1, n, id[u], id[v], add);
}
}
int main() {
IOS;
cin >> n;
for (int i = 1, a, b; i<n; ++i) {
cin >> a >> b;
e[a].push_back(b);
e[b].push_back(a);
}
dfs1(1, 0); dfs2(1, 1);
cin >> q;
while(q--) {
int o, l, r; cin >> o;
if (o==1) {
cin >> l >> r;
modify(l, r);
}
else if (o==2) {
cin >> l;
Node res = ask(1, 1, n, id[l]);
ll ans = id[l]*id[l]*res.lz1+res.lz2-2*id[l]*res.lz3;
cout << ans << endl;
}
}
return 0;
}
平衡树
fhq treap
bzoj3224 基本操作
const int maxn = 1e5+5;
struct Node {
int l,r;
int val,key;
int size;
} fhq[maxn];
int cnt,root;
std::mt19937 rnd(233);
inline int newnode(int val) {
fhq[++cnt] = {0, 0, val, rand(), 1};
return cnt;
}
inline void update(int now) {
fhq[now].size = fhq[fhq[now].l].size+fhq[fhq[now].r].size+1;
}
void split(int now, int val, int &x, int &y) {
if (!now) x = y = 0;
else {
if (fhq[now].val<=val) {
x = now;
split(fhq[now].r, val, fhq[now].r, y);
}
else {
y = now;
split(fhq[now].l, val, x, fhq[now].l);
}
update(now);
}
}
int merge(int x, int y) {
if (!x || !y) return x+y;
if (fhq[x].key>fhq[y].key) {
fhq[x].r = merge(fhq[x].r, y);
update(x);
return x;
}
else {
fhq[y].l = merge(x, fhq[y].l);
update(y);
return y;
}
}
int x,y,z;
inline void ins(int val) {
split(root, val, x, y);
root = merge(merge(x, newnode(val)), y);
}
inline void del(int val) {
split(root, val, x, z);
split(x, val-1, x, y);
y = merge(fhq[y].l, fhq[y].r);
root = merge(merge(x, y), z);
}
inline void getrank(int val) {
split(root, val-1, x, y);
cout << fhq[x].size+1 << endl;
root = merge(x, y);
}
inline void getnum(int rank) {
int now = root;
while(now) {
if (fhq[fhq[now].l].size+1==rank) break;
else if (fhq[fhq[now].l].size>=rank) now = fhq[now].l;
else {
rank -= fhq[fhq[now].l].size+1;
now = fhq[now].r;
}
}
cout << fhq[now].val << endl;
}
inline void pre(int val) {
split(root, val-1, x, y);
int now = x;
while(fhq[now].r) now = fhq[now].r;
cout << fhq[now].val << endl;
root = merge(x, y);
}
inline void nxt(int val) {
split(root, val, x, y);
int now = y;
while(fhq[now].l) now = fhq[now].l;
cout << fhq[now].val << endl;
root = merge(x, y);
}
int main() {
IOS; int __; cin >> __;
while(__--) {
int opt, x; cin >> opt >> x;
if (opt==1) ins(x); //插入x
else if (opt==2) del(x); //删除x(若有多个删除一个)
else if (opt==3) getrank(x); //查询数x的排名(若有多个相同的数输出最小的排名)
else if (opt==4) getnum(x); //查询排名为 x 的数值
else if (opt==5) pre(x); //求数值 x 的前驱(前驱定义为小于x的最大的数)
else nxt(x); //求数值 x 的后继(后继定义为大于x的最小的数)
}
return 0;
}
bzoj3223 区间翻转
const int maxn = 1e5+10;
int n, arr[maxn];
struct Node {
int l, r, val, key, sz;
bool rev;
} fhq[maxn];
int tot, rt;
mt19937 rnd(23333);
inline int newnode(int val) {
fhq[++tot] = {0, 0, val, (int)rnd(), 1};
return tot;
}
inline void push_up(int now) {
fhq[now].sz = fhq[fhq[now].l].sz+fhq[fhq[now].r].sz+1;
}
inline void push_down(int now) {
if (fhq[now].rev) {
if (fhq[now].l) {
auto &ls = fhq[fhq[now].l];
swap(ls.l, ls.r); ls.rev ^= 1;
}
if (fhq[now].r) {
auto &rs = fhq[fhq[now].r];
swap(rs.l, rs.r); rs.rev ^= 1;
}
fhq[now].rev = 0;
}
}
void split(int now, int sz, int &x, int &y) {
if (!now) x = y = 0;
else {
push_down(now);
if (fhq[fhq[now].l].sz<sz) {
x = now;
split(fhq[now].r, sz-fhq[fhq[now].l].sz-1, fhq[now].r, y);
}
else {
y = now;
split(fhq[now].l, sz, x, fhq[now].l);
}
push_up(now);
}
}
int merge(int x, int y) {
if (!x || !y) return x+y;
if (fhq[x].key<fhq[y].key) {
push_down(x);
fhq[x].r = merge(fhq[x].r, y);
push_up(x);
return x;
}
else {
push_down(y);
fhq[y].l = merge(x, fhq[y].l);
push_up(y);
return y;
}
}
void reverse(int l, int r) {
int x, y, z;
split(rt, l-1, x, y);
split(y, r-l+1, y, z);
fhq[y].rev ^= 1;
swap(fhq[y].l, fhq[y].r);
rt = merge(merge(x, y), z);
}
void get_ans(int now) {
push_down(now);
if (fhq[now].l) get_ans(fhq[now].l);
cout << fhq[now].val << ' ';
if (fhq[now].r) get_ans(fhq[now].r);
}
int main() {
IOS;
int n, m; cin >> n >> m;
for (int i = 1; i<=n; ++i) rt = merge(rt, newnode(i));
while(m--) {
int l, r; cin >> l >> r;
reverse(l, r);
}
get_ans(rt);
return 0;
}
bzoj2733 fhq treap启发式合并
const int maxn = 2e5+10;
struct Node {
int l, r, val, key, num, sz;
} fhq[maxn*40];
int idx, rt[maxn];
mt19937 rnd(233);
int newnode(int val, int i) {
fhq[++idx] = {0, 0, val, rnd()%MOD, i, 1};
return idx;
}
inline void push_up(int now) {
fhq[now].sz = fhq[fhq[now].l].sz+fhq[fhq[now].r].sz+1;
}
void split(int now, int val, int &x, int &y) {
if (!now) x = y = 0;
else {
if (fhq[now].val<=val) {
x = now;
split(fhq[now].r, val, fhq[now].r, y);
}
else {
y = now;
split(fhq[now].l, val, x, fhq[now].l);
}
push_up(now);
}
}
int merge(int x, int y) {
if (!x || !y) return x|y;
if (fhq[x].key>=fhq[y].key) {
fhq[x].r = merge(fhq[x].r, y);
push_up(x);
return x;
}
else {
fhq[y].l = merge(x, fhq[y].l);
push_up(y);
return y;
}
}
int get_num(int k, int i) {
int now = rt[i];
if (fhq[now].sz<k) return -1;
while(now) {
int sz = fhq[fhq[now].l].sz;
if (sz+1==k) break;
else if (sz+1>k) now = fhq[now].l;
else {
k -= sz+1;
now = fhq[now].r;
}
}
return fhq[now].num;
}
int x, y;
void ins(int i, int val, int ii) {
split(rt[i], val-1, x, y);
rt[i] = merge(merge(x, newnode(val, ii)), y);
}
int p[maxn], sz[maxn], arr[maxn];
int fnd(int x) {
return p[x]==x ? p[x]:p[x]=fnd(p[x]);
}
void uni(int a, int b) {
a = fnd(a), b = fnd(b);
if (a==b) return;
if (sz[a]<sz[b]) swap(a, b);
sz[a] += sz[b], p[b] = a;
return;
}
void dfs(int rr, int now) {
ins(rr, fhq[now].val, fhq[now].num);
if (fhq[now].l) dfs(rr, fhq[now].l);
if (fhq[now].r) dfs(rr, fhq[now].r);
}
void unit(int a, int b) {
if (sz[a]<sz[b]) swap(a, b);
sz[a] += sz[b], p[b] = a;
dfs(a, rt[b]);
}
int main() {
IOS;
int n, m; cin >> n >> m;
for (int i = 1; i<=n; ++i) {
cin >> arr[i];
p[i] = i, sz[i] = 1;
}
for (int i = 1, a, b; i<=m; ++i) {
cin >> a >> b;
uni(a, b);
}
for (int i = 1; i<=n; ++i) ins(fnd(i), arr[i], i);
int q; cin >> q;
while(q--) {
char op[10]; int a, b;
cin >> op >> a >> b;
if (op[0]=='Q') {
//cout << "!" << fnd(a) << endl;
//cout << sz[fnd(a)] << endl;
cout << get_num(b, fnd(a)) << endl;
}
else {
int fa = fnd(a), fb = fnd(b);
if (fa!=fb) unit(fa, fb);
}
}
return 0;
}
splay
AcWing 2437 平衡树插入,删除,区间修改,区间翻转,区间求和,区间求最大子段和
const int maxn = 1e6+10;
int n, m, a[maxn];
struct Node {
int s[2], v, p, sz;
int sum, sm, lm, rm;
int rev, same;
void init(int _v, int _p) {
//s0:左儿子 s1:右儿子
sum = sm = v = _v, p = _p;
lm = rm = max(_v, 0);
s[0] = s[1] = rev = same = 0;
//因为要回收再利用,所以都要初始化为0
sz = 1;
}
} tr[maxn];
int rt, q[maxn], tt;
inline void push_up(int u) {
Node &now = tr[u];
Node ls = tr[now.s[0]];
Node rs = tr[now.s[1]];
now.sz = ls.sz+rs.sz+1;
now.sum = ls.sum+rs.sum+now.v;
now.lm = max(ls.lm, ls.sum+rs.lm+now.v);
now.rm = max(rs.rm, rs.sum+ls.rm+now.v);
now.sm = max({ls.sm, rs.sm, ls.rm+now.v+rs.lm});
}
inline void push_down(int u) {
Node &now = tr[u];
Node &ls = tr[now.s[0]];
Node &rs = tr[now.s[1]];
if (now.same) {
now.same = now.rev = 0;
//如果u是叶子就不能更新了,也就是看u有没有儿子
if (now.s[0]) {
ls.same = 1;
ls.v = now.v;
ls.sum = ls.sz*now.v;
if (now.v>0) ls.sm = ls.lm = ls.rm = ls.sum;
//最大子段和至少要有一个数,所以ls.sm至少为now.v
else ls.sm = now.v, ls.lm = ls.rm = 0;
}
if (now.s[1]) {
rs.same = 1;
rs.v = now.v;
rs.sum = rs.sz*now.v;
if (now.v>0) rs.sm = rs.lm = rs.rm = rs.sum;
else rs.sm = now.v, rs.lm = rs.rm = 0;
}
}
else if (now.rev) {
ls.rev ^= 1;
rs.rev ^= 1;
swap(ls.s[0], ls.s[1]);
swap(rs.s[0], rs.s[1]);
swap(ls.lm, ls.rm);
swap(rs.lm, rs.rm);
now.rev = 0;
}
}
int build(int l, int r, int p) {
int mid = (l+r)>>1;
int u = q[tt--];
tr[u].init(a[mid], p);
if (l<mid) tr[u].s[0] = build(l, mid-1, u);
if (r>mid) tr[u].s[1] = build(mid+1, r, u);
push_up(u);
return u;
}
void rotate(int x) {
int y = tr[x].p, z = tr[y].p;
int k = tr[y].s[1]==x; //0: x是y的左儿子 1:x是y的右儿子
tr[z].s[tr[z].s[1]==y] = x, tr[x].p = z;
tr[y].s[k] = tr[x].s[k^1], tr[tr[x].s[k^1]].p = y;
tr[x].s[k^1] = y, tr[y].p = x;
push_up(y), push_up(x);
//这里不需要push_donw,能用到这个点说明之前get_k的之后已经把沿路的点都push_down过了
/*
x是y的左儿子:
y右旋
y是z的左儿子:
x设成z的左儿子
y是z的右儿子:
x设成z的右儿子
x的右儿子挂到y的左边
y设成x的右儿子
x是y的右儿子:
y左旋
y是z的左儿子:
x设成z的左儿子
y是z的右儿子
x设成z的右儿子
x的左儿子挂到y的右边
y设成x的左儿子
*/
}
void splay(int x, int k) {
while(tr[x].p!=k) {
int y = tr[x].p, z = tr[y].p;
if (z!=k)
if ((tr[y].s[1]==x)^(tr[z].s[1]==y)) rotate(x);
else rotate(y);
rotate(x);
}
if (!k) rt = x;
}
int get_k(int k) {
int u = rt;
while(u) {
push_down(u);
int sz = tr[tr[u].s[0]].sz;
if (sz>=k) u = tr[u].s[0];
else if (sz+1==k) return u;
else k -= sz+1, u = tr[u].s[1];
}
return 0;
}
void rec(int u) {
if (!u) return;
if (tr[u].s[0]) rec(tr[u].s[0]);
if (tr[u].s[1]) rec(tr[u].s[1]);
q[++tt] = u;
}
int main() {
IOS;
for (int i = 1; i<maxn; ++i) q[++tt] = i;
cin >> n >> m;
for (int i = 1; i<=n; ++i) cin >> a[i];
a[0] = a[n+1] = tr[0].sm = -INF;
rt = q[tt]; build(0, n+1, 0);
while(m--) {
char op[20]; int pos, tot;
cin >> op;
if (!strcmp(op, "INSERT")) {
cin >> pos >> tot;
//因为左边有个哨兵,所以l和r都要加1
int L = get_k(pos+1), R = get_k(pos+2);
splay(L, 0), splay(R, L);
//先把l-1 splay到根节点,再把r+1 splay到l-1 的下面,r+1的左子树就是区间l到r
for (int i = 0; i<tot; ++i) cin >> a[i];
tr[R].s[0] = build(0, tot-1, R);
push_up(R), push_up(L);
}
else if (!strcmp(op, "DELETE")) {
cin >> pos >> tot;
int L = get_k(pos), R = get_k(pos+tot+1);
splay(L, 0), splay(R, L);
rec(tr[R].s[0]);
tr[R].s[0] = 0;
push_up(R), push_up(L);
}
else if (!strcmp(op, "MAKE-SAME")) {
int c;
cin >> pos >> tot >> c;
int L = get_k(pos), R = get_k(pos+tot+1);
splay(L, 0), splay(R, L);
Node &now = tr[tr[R].s[0]];
now.same = 1;
now.v = c;
now.sum = now.sz*c;
if (c>0) now.sm = now.lm = now.rm = now.sum;
else now.sm = c, now.lm = now.rm = 0;
push_up(R), push_up(L);
}
else if (!strcmp(op, "REVERSE")) {
cin >> pos >> tot;
int L = get_k(pos), R = get_k(pos+tot+1);
splay(L, 0), splay(R, L);
Node &now = tr[tr[R].s[0]];
now.rev ^= 1;
swap(now.s[0], now.s[1]);
swap(now.lm, now.rm);
push_up(R), push_up(L);
}
else if (!strcmp(op, "GET-SUM")) {
cin >> pos >> tot;
int L = get_k(pos), R = get_k(pos+tot+1);
splay(L, 0), splay(R, L);
cout << tr[tr[R].s[0]].sum << endl;
}
else if (!strcmp(op, "MAX-SUM")) {
cout << tr[rt].sm << endl;
}
}
return 0;
}
AcWing 1063 并查集+平衡树启发式合并求集合第\(k\)小
const int maxn = 1e5+10;
int n, m, a[maxn], p[maxn];
int find(int x) {
return p[x]==x ? p[x]:p[x]=find(p[x]);
}
int rt[maxn], idx;
struct Node {
int s[2], sz, v, p, num;
void init(int _v, int _num, int _p) {
v = _v, num = _num, p = _p;
sz = 1;
}
} tr[maxn*40];
inline void push_up(int u) {
tr[u].sz = tr[tr[u].s[0]].sz+tr[tr[u].s[1]].sz+1;
}
void rotate(int x) {
int y = tr[x].p, z = tr[y].p;
int k = tr[y].s[1]==x;
tr[z].s[tr[z].s[1]==y] = x, tr[x].p = z;
tr[y].s[k] = tr[x].s[k^1], tr[tr[x].s[k^1]].p = y;
tr[x].s[k^1] = y, tr[y].p = x;
push_up(y), push_up(x);
}
void splay(int &rt, int x, int k) {
while(tr[x].p!=k) {
int y = tr[x].p, z = tr[y].p;
if (z!=k)
if ((tr[y].s[1]==x)^(tr[z].s[1]==y)) rotate(x);
else rotate(y);
rotate(x);
}
if (!k) rt = x;
}
void insert(int &rt, int v, int num) {
int p = 0, u = rt;
while(u) p = u, u = tr[u].s[v>tr[u].v];
u = ++idx;
if (p) tr[p].s[v>tr[p].v] = u;
tr[u].init(v, num, p);
splay(rt, u, 0);
}
void merge(int u, int &rt) {
if (tr[u].v==INF || tr[u].v==-INF) return;
insert(rt, tr[u].v, tr[u].num);
if (tr[u].s[0]) merge(tr[u].s[0], rt);
if (tr[u].s[1]) merge(tr[u].s[1], rt);
}
int query(int u, int k) {
while(u) {
int sz = tr[tr[u].s[0]].sz;
if (sz>=k) u = tr[u].s[0];
else if (sz+1==k) return tr[u].num;
else k -= sz+1, u = tr[u].s[1];
}
return -1;
}
int main() {
IOS;
cin >> n >> m;
for (int i = 1; i<=n; ++i) cin >> a[i];
for (int i = 1; i<=n; ++i) p[i] = i;
while(m--) {
int a, b; cin >> a >> b;
p[find(a)] = find(b);
}
for (int i = 1; i<=n; ++i) {
int pi = find(i);
if (!rt[pi]) {
insert(rt[pi], -INF, i);
insert(rt[pi], INF, i);
}
insert(rt[pi], a[i], i);
}
int q; cin >> q;
while(q--) {
char op[10]; int a, b;
cin >> op >> a >> b;
if (op[0]=='B') {
int fa = find(a);
int fb = find(b);
if (fa!=fb) {
if (tr[rt[fa]].sz<=tr[rt[fb]].sz) {
p[fa] = fb;
merge(rt[fa], rt[fb]);
}
else {
p[fb] = fa;
merge(rt[fb], rt[fa]);
}
}
}
else {
int fa = find(a);
if (tr[rt[fa]].sz-2<b) cout << -1 << endl;
else cout << query(rt[fa], b+1) << endl;
}
}
return 0;
}
dsu on tree
Gym - 102832F \(i\)和\(j\)是树上不同的两个点,计算下面公式的值
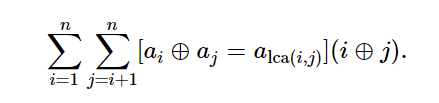
拆位处理下标异或即可。
const int maxn = 2e5+10;
const int maxm = 2e6+10;
int n, val[maxn];
vector<int> e[maxn];
int sz[maxn], mx[maxn];
void dfs(int u, int p) {
sz[u] = 1; //求重儿子
for (auto v : e[u]) {
if (v==p) continue;
dfs(v, u);
sz[u] += sz[v];
if (sz[mx[u]]<sz[v]) mx[u] = v;
}
}
int flag, cnt[maxm][20], num[maxm]; ll ans;
void count(int u, int p, int x, int f) {
if (f==0) { //f = 0,计算贡献
for (int i = 0; i<20; ++i) {
if (u>>i&1) ans += (1LL<<i)*(num[x^val[u]]-cnt[x^val[u]][i]);
else ans += (1LL<<i)*cnt[x^val[u]][i];
}
}
else { //f = 1 or -1,加上or删除贡献
num[val[u]] += f;
for (int i = 0; i<20; ++i)
if (u>>i&1) cnt[val[u]][i] += f;
}
for (auto v : e[u]) {
if (v==p || v==flag) continue; //之前计算的重儿子信息保留了,不再计算
count(v, u, x, f);
}
}
void dsu(int u, int p, bool keep) {
for (auto v : e[u]) {
if (v==p || v==mx[u]) continue;
dsu(v, u, 0); //先计算轻儿子
}
if (mx[u]) { //有重儿子就计算并保留信息
dsu(mx[u], u, 1);
flag = mx[u];
}
++num[val[u]]; //加上当前节点的信息,因为没有$u$是$v$的$lca%,俩值异或还等于$u$自己的情况(没有为0的值)
for (int i = 0; i<20; ++i)
if (u>>i&1) ++cnt[val[u]][i];
for (auto v : e[u]) {
if (v==p || v==flag) continue;
count(v, u, val[u], 0);
count(v, u, val[u], 1);
}
flag = 0;
if (!keep) count(u, p, val[u], -1); //如果当前节点不是父亲节点的重儿子,删除贡献
}
int main() {
IOS;
cin >> n;
for (int i = 1; i<=n; ++i) cin >> val[i];
for (int i = 1; i<n; ++i) {
int a, b; cin >> a >> b;
e[a].push_back(b);
e[b].push_back(a);
}
dfs(1, 0);
dsu(1, 0, 0);
cout << ans << endl;
return 0;
}
数论
同余定理
同余定理是数论中的重要概念。给定一个正整数m,如果两个整数a和b满足\((a-b)\)能够被m整除,即\((a-b) /div m\)得到一个整数,那么就称整数a与b对模m同余,记作\(a≡b(mod m)\)。
同余符号
两个整数a、b,若它们除以整数m所得的余数相等,则称a与b对模m同余或a同余于b模m。记作\(a≡b(mod m)\)
【定义】 设m是大于1的正整数,a、b是整数,如果\(m|(a-b)\),则称a与b关于模m同余,记作\(a≡b(mod m)\)。显然有如下事实:
若\(a≡0(mod m)\),则\(m|a\);
\(a≡b(mod m)\)等价于a与b分别用m去除,余数相同。
证明
充分性:
若a和b用m相除留下相同的余数r,则 \(a = q_1 \times m + r, b = q_2 \times m + r\),q1和q2为某两个整数,由此的\(a-b =(q_1 \times m + r) - (q_2 \times m - r ) = m \times (q1 - q2)\),根据整除定义,我们有\(m|(a-b)\),由同余式定义得出结论:\(a≡b(mod m)\)
必要性:
若a和b用m相除留下相同的余数r,则\(a = q_1 \times m + r, b = q_2 \times m + r\),所以\(a-b=m \times (q1-q2)\) 故 \(m|(a-b)\)。
同余性质
反身性:\(a≡a (mod m)\)
对称性: 若\(a≡b(mod m)\),则\(b≡a(mod m)\)
传递性: 若\(a≡b(mod m)\),\(b≡c(mod m)\),则\(a≡c(mod m)\)
同余式相加:若\(a≡b(mod m)\),\(b≡c(mod m)\),则\(a ± c≡b ± d(mod m)\)
同余式相乘:若\(a≡b(mod m),b≡c(mod m)\),则\(a \times c≡b \times d(mod m)\)
线性运算:如果\(a≡b(mod m),c≡d(mod m)\),那么\(a ± c≡b ± d(mod m)\),且\(a \times c≡b \times d(mod m)\)
除法:若\(a \times c ≡ b \times c (mod m) c≠0\)则 \(a ≡ b (mod m/gcd(c,m))\) 其中gcd(c,m)表示c,m的最大公约数。特殊地 ,gcd(c,m)=1 则\(a ≡ b (mod m)\)
幂运算:如果\(a ≡ b (mod m)\),那么\(a^n ≡ b^n (mod m)\)
若\(a ≡ b (mod m),n|m\),则 \(a ≡ b (mod n)\)
若\(a ≡ b (mod m) (i=1,2…n)\) 则 \(a ≡ b (mod [m1,m2,…mn])\) 其中[m1,m2,…mn]表示m1,m2,…mn的最小公倍数
除法取模
除法取模有一个(\(b\)可以不是质数)公式: \(a\div b \mod p = (a\mod (p\times b))\div b\)
- 证明:
- \(a\div b = k\times p + x, (x<p)\)
- 两边同乘\(b\)可得: \(a = k\times p \times b + x\times b\)
- 再对\(a\)取模: \(a \mod (p\times b) = x\times b\)
- 两边同除\(b\)得: \((a\mod (p\times b))\div b = x\)
01分数规划
int n, k;
ll a[maxn], b[maxn];
double tmp[maxn];
bool check(double x) {
for (int i = 1; i<=n; ++i) tmp[i] = a[i]-x*b[i];
sort(tmp+1, tmp+n+1, greater<double>());
double sum = 0;
for (int i = 1; i<=n-k; ++i) sum += tmp[i];
return sum >= -eps;
}
int main() {
while(~scanf("%d%d", &n, &k) && (n||k)) {
for (int i = 1; i<=n; ++i) scanf("%lld", &a[i]);
for (int i = 1; i<=n; ++i) scanf("%lld", &b[i]);
double l = 0, r = 1e18;
for (int i = 1; i<=100; ++i) {
double mid = (l+r)/2;
if (check(mid)) l = mid;
else r = mid;
}
printf("%.f\n", l*100);
}
return 0;
}
exgcd
ll x, y;
void exgcd(ll a, ll b) {
if (!b) {
x = 1, y= 0;
return;
}
exgcd(b, a%b);
ll t = x; x = y;
y = t - a/b*y;
}
excrt
ll exgcd(ll a, ll b, ll &x, ll &y){
if(!b){
x = 1, y = 0;
return a;
}
ll d = exgcd(b, a % b, y, x);
y -= a / b * x;
return d;
}
ll excrt() {
ll lcm = m[0], ans = a[0];
for(int i = 1; i<n; ++i) {
ll lcm_a = ((a[i]-ans)%m[i]+m[i])%m[i], x, y, k = lcm;
ll gcd = exgcd(lcm, m[i], x, y), t = m[i]/gcd;
if ((a[i]-ans) % gcd) return -1;
x = (x*lcm_a/gcd%t+t)%t;
lcm = lcm*t,ans = (ans + k*x)%lcm;
}
ans = (ans%lcm+lcm)%lcm;
return ans ? ans:lcm;
}
线性求逆元
Inv[1] = 1;
for(int i = 2; i <= n; ++i)
Inv[i] = (p - p / i)*Inv[p % i]%p;
线性求阶乘逆元
int inv(int b, int p) {
int a, k;
exPower( b, p, a, k );
if( a < 0 ) a += p;
return a;
}
void init(int n) {
Fact[ 0 ] = 1;
for( int i = 1; i <= n; ++i ) Fact[ i ] = Fact[ i - 1 ] * i % Mod;
INV[ n ] = inv( Fact[ n ], Mod );
for( int i = n - 1; i >= 0; --i ) INV[ i ] = INV[ i + 1 ] * ( i + 1 ) % Mod;
return;
}
欧拉定理
若\(n,a\)为正整数,且\(n,a\)互质,则\(a^{\phi(n)} \equiv 1(mod\ n)\)
广义欧拉降幂
卢卡斯定理
ll C(ll n, ll m){
if(m>n) return 0;
return fac[n]*qp(fac[m],mod-2)%mod*qp(fac[n-m],mod-2)%mod;
}
ll lucas(ll n,ll m){
if(!m) return 1;
return lucas(n/mod,m/mod)*C(n%mod,m%mod)%mod;
}
矩阵快速幂
int n, ans[2][2], res[2][2], tmp[2][2];
void mul(int a[][2], int b[][2]) {
zero(tmp);
for (int i = 0; i<2; ++i)
for (int j = 0; j<2; ++j)
for (int k = 0; k<2; ++k)
tmp[i][j] = (1LL*tmp[i][j]+1LL*a[i][k]*b[k][j]%MOD)%MOD;
memcpy(a, tmp, sizeof(tmp));
}
void mxqp(ll y) {
ans[0][0] = ans[1][1] = 1; ans[0][1] = ans[1][0] = 0; //单位矩阵
res[0][0] = res[0][1] = res[1][0] = 1; res[1][1] = 0; //用来算斐波那契数列
while(y) {
if (y&1) mul(ans, res);
mul(res, res);
y >>= 1;
}
}
acwing1305 矩阵快读幂解决kmp+dp问题
const int maxn = 25;
const int maxm = 1e6+10;
char str[maxn];
int n, m, k, nxt[maxn];
ll res[maxn][maxn];
void get_nxt() {
int i = 1, j = 0;
nxt[i] = j;
while(i<m) {
while(j && str[i]!=str[j]) j = nxt[j];
nxt[++i] = ++j;
}
}
void get_res() {
for (int i = 0; i<m; ++i)
for (int c = '0'; c<='9'; ++c) {
int j = i+1;
while(j && str[j]!=c) j = nxt[j];
if (j<m) {
++res[i][j];
//能从表示匹配长度为i结尾为c时转移到长度为匹配j的状态
}
}
}
void mult(ll a[maxn][maxn], ll b[maxn][maxn], ll m) {
ll c[maxn][maxn]; clr(c, 0);
for (int i = 0; i<maxn; ++i)
for (int j = 0; j<maxn; ++j)
for (int k = 0; k<maxn; ++k)
c[i][j] = (c[i][j]+a[i][k]*b[k][j]%m)%m;
memcpy(a, c, sizeof(c));
}
ll qp(int n, int mod) {
get_nxt();
get_res();
ll ans[maxn][maxn] = {1};
while(n) {
if (n&1) mult(ans, res, mod);
mult(res, res, mod);
n >>= 1;
}
ll sum = 0;
for (int i = 0; i<m; ++i) sum = (sum+ans[0][i])%mod;
return sum;
}
int main(void) {
IOS;
cin >> n >> m >> k >> str+1;
cout << qp(n, k) << endl;
return 0;
}
大数分解质因数与素数判定
const int S = 20; //随机算法判定次数,S越大,判错概率越小
//龟速乘计算 (a*b)%c, a,b,c <2^63
ll mult_mod(ll a, ll b, ll c) {
a %= c, b %=c;
ll res = 0;
while(b) {
if (b&1) {
res += a;
if (res>c) res -= c;
}
a <<= 1;
if (a>c) a -= c;
b >>= 1;
}
return res;
}
//计算 x^n %c
ll pow_mod(ll x, ll n, ll c) {
x %= c;
if (n==1) return x;
ll ans = 1;
while(n) {
if (n&1) ans = mult_mod(ans, x, c);
x = mult_mod(x, x, c);
n >>= 1;
}
return ans;
}
//通过a^(n-1)=1(mod n) 验证n是不是合数
//以a为基, n-1=x*(2^t) 中间使用二次判断
//一定是合数返回1,不一定返回0
bool check(ll a, ll n, ll x, ll t) {
ll res = pow_mod(a, x, n), lst = res;
for (int i = 1; i<=t; ++i) {
res = mult_mod(res, res, n);
if (res==1 && lst!=1 && lst!=n-1) return 1;
lst = res;
}
return res!=1;
}
// Miller_Rabin()算法素数判定
//是素数返回1.(可能是伪素数,但概率极小)
//合数返回0
bool miller_rabin(ll n) {
if (n<2) return 0;
if (n==2) return 1;
if (~n&1) return 0; //偶数
ll x = n-1, t = 0;
while(~x&1) x >>= 1, ++t;
srand(time(0));
for (int i = 0; i<S; ++i) {
ll a = rand()%(n-1)+1;
if (check(a, n, x, t)) return 0; //合数
}
return 1;
}
//pollard_rho 算法进行质因数分解
ll fac[100]; //质因数分解结果(刚返回时是无序的)
int tol; //质因数的个数。数组小标从0开始
ll gcd(ll a, ll b) {
if (a==0) return 1;
if (a<0) return gcd(-a, b);
while(b) {
ll t = a%b;
a = b;
b = t;
}
return a;
}
//找出一个因子
ll pollard_rho(ll n, ll c) {
ll i = 1, k = 2;
srand(time(0));
ll x0 = rand()%(n-1)+1, y = x0;
while(1) {
++i;
x0 = (mult_mod(x0, x0, n)+c)%n;
ll d = gcd(y-x0, n);
if (d!=1 && d!=n) return d;
if (y==x0) return n;
if (i==k) y = x0, k += k;
}
}
//对n进行素因子分解,存入fac,k设置107左右即可,也可以随机数取[1,n]内的数
void findfac(ll n, int k) {
if (n==1) return;
if (miller_rabin(n)) {
fac[tol++] = n;
return;
}
ll p = n;
int c = k;
while(p>=n) p = pollard_rho(p, c--); //k值变化,防止死循环
findfac(p, k);
findfac(n/p, k);
}
ll col(ll n, ll x) {
ll sum = 0;
while(n) {
sum += n/x;
n /= x;
}
return sum;
}
线性基
普通线性基
HDU - 3949 求n个数的子序列的最大异或和
求出n个数的线性基并排序,然后将k二进制异或上线性基中对应的代表元素即可。
const int maxn = 2e5+10;
ll arr[maxn];
vector<ll> b; //b中存的每个二进制位的代表元素
void insert(ll x) { //设x在线性基中(不是原来的数字)二进制表示为1的最高位为y
for (auto v : b) x = min(x, x^v); //x的二进制位中小于y的二进制位不能和其他代表元素同为1
for (auto &v : b) v = min(v, v^x); //b中元素的二进制位中第y位的二进制位不能和x同为1
if (x) b.push_back(x);
}
int main(void) {
IOS; int kase = 0;
int __; cin >> __;
while(__--) {
cout << "Case #" << ++kase << ":" << endl;
int n; cin >> n;
b.clear();
for (int i = 1; i<= n; ++i) {
cin >> arr[i];
insert(arr[i]);
}
sort(b.begin(), b.end());
int q; cin >> q;
while(q--) {
ll k; cin >> k;
if (b.size()<n) --k;
if (k+1>1LL<<b.size()) cout << -1 << endl;
else {
ll sum = 0;
for (int i = 0; i<b.size(); ++i)
if (k>>i&1) sum ^= b[i];
cout << sum << endl;
}
}
}
return 0;
}
bitset优化
bzoj 1923 用01串表示用到了几个数,后面再用0或1表示这几个数相加是奇数还是偶数,问最少需要几次能唯一判断出每个数的奇偶。
如果线性基的每一位都有一个代表元素,说明有唯一解。
const int maxn = 2e3+10;
const int maxm = 1e6+10;
int n, m, cnt, vis[maxn];
bitset<maxn> s[maxn];
int insert(bitset<maxn> t) {
for (int i = 1; i<=n; ++i) {
if (!t[i]) continue;
if (vis[i]) t ^= s[i];
else {
vis[i] = 1;
s[i] = t;
++cnt;
return 1;
}
}
return 0;
}
int main() {
IOS;
cin >> n >> m;
int ans = 0;
for (int i = 1; i<=m; ++i) {
string s; int t; cin >> s >> t;
bitset<maxn> res;
for (int j = 0; j<n; ++j)
if (s[j]=='1') res.set(j+1);
res.set(n+1, t);
if (insert(res)) ans = i;
}
if (cnt<n) cout << "Cannot Determine" << endl;
else {
cout << ans << endl;
for (int i = n; i>=1; --i)
for (int j = i-1; j>=1; --j)
if (s[j][i]) s[j] ^= s[i];
for (int i = 1; i<=n; ++i)
cout << (s[i][n+1] ? "?y7M#":"Earth") << endl;
}
return 0;
}
十进制线性基
bzoj4004 用最小的花费表示出所有装备,求最多数量以及最多数量下的最小花费
const int maxn = 5e2+10;
int n, m;
struct E {
int a[maxn];
bool operator < (E b) const {
return a[m+1]<b.a[m+1];
}
} e[maxn];
int base[maxn], cnt; ll sum = 0;
ll qp(ll x, ll y) {
ll res = 1;
while(y) {
if (y&1) res = res*x%MOD;
x = x*x%MOD;
y >>= 1;
}
return res;
}
void insert(int x) {
for (int i = 1; i<=m; ++i) {
if (!e[x].a[i]) continue;
if (!base[i]) {
base[i] = x;
++cnt;
sum += e[x].a[m+1];
break;
}
else {
int j = base[i];
ll t = 1ll*e[x].a[i]*qp(e[j].a[i], MOD-2)%MOD;
for (int k = m; k>=i; --k) {
e[x].a[k] = (1ll*e[x].a[k]-t*e[j].a[k])%MOD;
e[x].a[k] = (e[x].a[k]+MOD)%MOD;
}
}
}
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
cin >> n >> m;
for (int i = 1; i<=n; ++i)
for (int j = 1; j<=m; ++j)
cin >> e[i].a[j];
for (int i = 1; i<=n; ++i) cin >> e[i].a[m+1]; //m+1是花费
sort(e+1, e+n+1);
for (int i = 1; i<=m; ++i) insert(i);
cout << cnt << ' ' << sum << endl;
return 0;
}
高斯消元
acwing207 高斯消元求线性方程组
const int maxn = 15;
const int maxm = 1e6+10;
int n;
double a[maxn][maxn], b[maxn][maxn];
void gauss() {
//转化为下三角矩阵
for (int r = 1, c = 1; c<=n; c++, r++) {
//找主元
int t = r;
for (int i = r+1; i<=n; ++i)
if (fabs(b[i][c])>fabs(b[t][c])) t = i;
//交换
for (int i = c; i<=n+1; ++i) swap(b[t][i], b[r][i]);
//归一化
for (int i = n+1; i>=c; --i) b[r][i] /= b[r][c];
//消
for (int i = r+1; i<=n; ++i)
for (int j = n+1; j>=c; --j)
b[i][j] -= b[i][c]*b[r][j];
}
//转化为对角矩阵
for (int i = n; i>1; --i)
for (int j = i-1; j; --j) {
b[j][n+1] -= b[i][n+1]*b[j][i];
b[j][i] = 0;
}
}
int main(void) {
IOS;
cin >> n;
for (int i = 1; i<=n+1; ++i)
for (int j = 1; j<=n; ++j)
cin >> a[i][j];
for (int i = 2; i<=n+1; ++i)
for (int j = 1; j<=n; ++j) {
b[i-1][j] = 2*(a[i][j]-a[1][j]);
b[i-1][n+1] += a[i][j]*a[i][j]-a[1][j]*a[1][j];
}
gauss();
for (int i = 1; i<=n; ++i) cout << fixed << setprecision(3) << b[i][n+1] << (i==n ? '\n':' ');
return 0;
}
acwing208 高斯消元求异或方程组
const int maxn = 1e2+10;
const int maxm = 1e6+10;
int n, a[maxn][maxn];
int gauss() {
int r, c;
for (r = 1, c = 1; c<=n; ++c) {
//找主元
int t = r;
for (int i = r+1; i<=n; ++i)
if (a[i][c]) t = i;
if (!a[t][c]) continue;
//交换
for (int i = c; i<=n+1; ++i) swap(a[t][i], a[r][i]);
//消
for (int i = r+1; i<=n; ++i)
for (int j = n+1; j>=c; --j)
a[i][j] ^= a[i][c]&a[r][j];
++r;
}
int res = 1;
if (r<n+1) {
for (int i = r; i<=n; ++i) {
if (a[i][n+1]) return -1;
res *= 2;
}
}
return res;
}
int main() {
IOS;
int __; cin >> __;
while(__--) {
clr(a, 0);
cin >> n;
for (int i = 1; i<=n; ++i) cin >> a[i][n+1];
for (int i = 1; i<=n; ++i) {
int num; cin >> num;
a[i][n+1] ^= num;
a[i][i] = 1;
}
int x, y;
while(cin >> x >> y && (x||y)) {
a[y][x] = 1;
}
int ans = gauss();
if (ans==-1) cout << "Oh,it's impossible~!!" << endl;
else cout << ans << endl;
}
return 0;
}
高斯消元求异或方程组bitset优化
bzoj 1923 用01串表示用到了几个数,后面再用0或1表示这几个数相加是奇数还是偶数,问最少需要几次能唯一判断出每个数的奇偶。
高斯消元记录一下找一下每个主元所在的最小行号,记录其最大值即可。
const int maxn = 2e3+10;
const int maxm = 1e6+10;
int n, m, ans;
bitset<maxn> a[maxn];
int gauss() {
int r, c;
for (r = 1, c = 1; c<=n; ++c) {
//找主元
int t = r;
for (int i = r; i<=m; ++i)
if (a[i][c]==1) {
t = i;
break;
}
if (!a[t][c]) return 0;
ans = max(ans, t);
//交换
if (r!=t) swap(a[r], a[t]);
//消
for (int i = 1; i<=m; ++i)
if (i!=r && a[i][c]==1) a[i] ^= a[r];
//本身是要把r下面的第c列消为0,只有a[i][c]是1才消,是0就不消了
//消出来的结果就是对角矩阵
++r;
}
return 1;
}
int main() {
IOS;
cin >> n >> m;
for (int i = 1; i<=m; ++i) {
string s; int t; cin >> s >> t;
for (int j = 0; j<n; ++j)
if (s[j]=='1') a[i].set(j+1);
a[i].set(n+1, t);
}
int x = gauss();
if (!x) cout << "Cannot Determine" << endl;
else {
cout << ans << endl;
for (int i = 1; i<=n; ++i)
cout << (a[i][n+1] ? "?y7M#":"Earth") << endl;
}
return 0;
}
组合数学
常用组合数计算公式
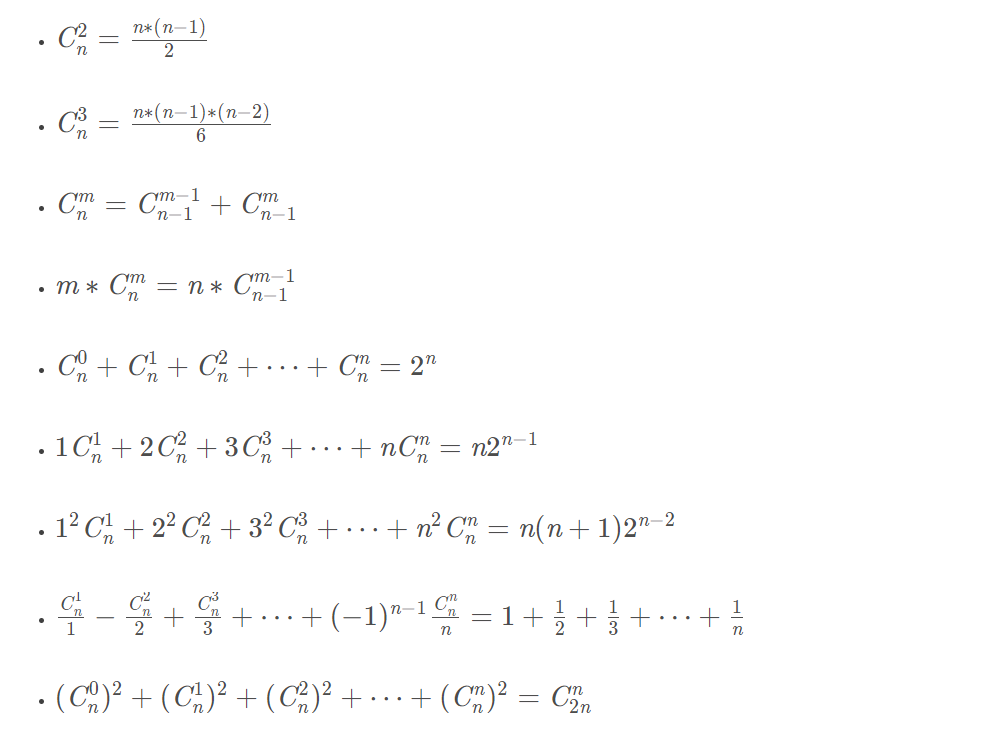
利用分解质因数计算两个组合数相减
一个一个乘算大数。
const int maxn = 100010;
int p[maxn], cnt;
bool st[maxn];
int a[maxn], b[maxn];
void init(int n) {
for (int i = 2; i <= n; ++i) {
if (!st[i]) p[cnt++] = i;
for (int j = 0; i*p[j]<=n; ++j) {
st[i*p[j]] = true;
if (i%p[j] == 0) break;
}
}
}
void sub(int a[], int al, int b[], int bl) { //高精度减法
for (int i = 0, t = 0; i<al; ++i) {
a[i] -= t+b[i];
if (a[i]<0) a[i] += 10, t = 1;
else t = 0;
}
}
void mul(int r[], int &len, int x) { //高精度乘低精度
int t = 0;
for (int i = 0; i<len; ++i) {
t += r[i]*x;
r[i] = t%10;
t /= 10; //t始终不会超过x*10
}
while (t) {
r[len++] = t%10;
t /= 10;
}
}
int get(int n, int p) { //求n!里面有多少个p
int s = 0;
while (n) s += n/p, n /= p;
return s;
}
int C(int x, int y, int r[]) { //分解质因数求阶乘
int len = 1;
r[0] = 1;
for (int i = 0; i < cnt; ++i) {
int t = p[i];
int s = get(x, t) - get(y, t) - get(x-y, t); //算出当前质数的幂次
while (s--) mul(r, len, t); //计算p_1^x_1乘p_2^x_2乘...
}
return len;
}
int main() {
init(maxn-1);
int n, m;
cin >> n >> m;
int al = C(n+m, m, a);
int bl = C(n+m, n+1, b);
sub(a, al, b, bl);
int k = al-1;
while (!a[k] && k>0) k--; //去掉前导0
while (k>=0) printf("%d", a[k--]);
return 0;
}
题目要求取模,利用快速幂计算
const int maxn = 1e2+10;
const int maxm = 1e5+10;
ll arr[maxn], down;
ll qp(ll x, ll y) {
ll ans = 1;
while(y) {
if (y&1) ans = ans*x%MOD;
x = x*x%MOD;
y >>= 1;
}
return ans;
}
ll C(ll x, ll y) {
if (x<y) return 0;
ll f = 1;
for (ll i = x; i>x-y; --i) f = i%MOD*f%MOD;
return f*down%MOD;
}
int main() {
IOS;
ll n, m; cin >> n >> m;
for (int i = 0; i<n; ++i) cin >> arr[i];
down = 1;
for (int i = 1; i<n; ++i) down = down*i%MOD;
down = qp(down, MOD-2);
ll sum = 0;
for (int i = 0; i<(1<<n); ++i) {
int sign = 1;
ll a = n+m-1, b = n-1;
for (int j = 0; j<n; ++j)
if (i>>j&1) {
sign *= -1;
a -= arr[j]+1;
}
sum = (sum+sign*C(a, b)+MOD)%MOD;
}
cout << sum << endl;
return 0;
}
求不定方程的解
相当于把n个球完全放入m个桶里面,如果都要大于0的话,结果就是\(c(n-1, m-1)\),即用\(m-1\)个隔板把\(n\)个1小球隔开。如果可以等于0的话,先每个桶里加1个球,即可转化为要求大于0的情况,结果就是\(c(n+m-1, m-1)\)。
求不等式的解
与上面情况类似,不同的是,因为不用完全放入,所以可以再加一个隔板,取的数字就是每个隔板前面的数,最后一个隔板后面的数舍弃了。
卡特兰数
定义:\(C(n)\)表示,从原点出发,每次向x或y轴正方向移动1单位,到达点(n,n),且在移动过程中不越过第一象限平分线的移动方案数。
通项公式:\(C(n) = c(2n, n)-c(2n, n+1)\)
推导:总的方案数是\(c(2n, n)\), 任何一个非法方案必定由一个点过直线\(y=x+1\),把这个方案的图形与直线相交的点后面的部分沿直线\(y\)做轴对称翻转,其最后的点肯定都落在点(n,n)关于直线\(y\)对称的点上(因为原来的终点都是(n,n))。
怎么算对称的点呢?把直线\(y\)下移可以得到\(y’ = x\),对于\(y’\)来说,其对称点就是横纵坐标颠倒一下,算出来点(n,n)下移一格的点(n, n-1)关于\(y’\)的对称点为(n-1, n),然后再上移一格得到(n-1, n+1),得到\(y\)的对称点,然后到终点的方案数减去到对称点的方案数即是答案。
卡特兰数的前几项:1,1,2,5,14,42,132...
拓展:n+m个人排队买票,并且满足n≥m,票价为50元,其中n个人有且仅有一张50元钞票,m个人有且仅有一张100元钞票,初始时候售票窗口没有钱,问有多少种排队的情况数能够让大家都买到票。
如果n=m可以直接用Catalan数解决,也就是将有50元的人看成是上述应用中的左括号,有100元的人看成是右括号。
对与n>m的情况,假设所有人都可以买到票的情况数是\(A_{n,m}\),不能让每个人都买到的情况数是\(B_{n,m}\),设最早买不到票的人为p,他一定手持100元且售票处没有50元,那么这时将前p个人的钱从50元变成100元,从100元变成50元(不考虑顺序,所以没有影响),这时候就有n+1个人有50元,m−1个有100元的,所以就得到\(B_{n,m} = c(n+m, n+1)\),那么\(A_{n,m} = c(n+m, n)-c(n+m, n+1)\)。从几何的角度看,到p点肯定手持100元的人比手持50的人多一个,也就是与直线\(y = x+1\)相交,按照前面的方法可以算出点(n,m)与直线\(y\)的对称点为(m-1, n+1),然后答案就是\(c(n+m, n)-c(n+m, n+1)\)。
图论
求欧拉回路
const int maxn = 2e5+10;
const int maxm = 2e6+10;
int t, n, m;
struct E {
int to, nxt;
} e[maxm];
int h[maxn], tot = 1, in[maxn], out[maxn];
void add(int u, int v) {
e[++tot] = {v, h[u]};
h[u] = tot;
}
int cnt, arr[maxn];
bool vis[maxm];
void dfs(int u) {
for (int i = h[u]; i; i=h[u]) {
h[u] = e[i].nxt;
if (vis[i]) continue;
vis[i] = 1;
int tt = i-1;
if (t==1) { //t=1无向图,否则有向图
tt = i/2;
vis[i^1] = 1; //这里的tot从2开始,不是从0开始
if (i&1) tt = -tt;; //这里是题目要求反向边取负数
}
dfs(e[i].to);
arr[++cnt] = tt;
}
}
int main(void) {
IOS;
cin >> t >> n >> m;
for (int i = 1, a, b; i<=m; ++i) {
cin >> a >> b;
add(a, b);
if (t==1) add(b, a);
++in[b], ++out[a];
}
if (t==1) {
for (int i = 1; i<=n; ++i)
if (in[i]+out[i]&1) {
cout << "NO" << endl;
return 0;
}
}
else {
for (int i = 1; i<=n; ++i)
if (in[i]!=out[i]) {
cout << "NO" << endl;
return 0;
}
}
for (int i = 1; i<=n; ++i)
if (h[i]) {
dfs(i);
break;
}
if (cnt!=m) {
cout << "NO" << endl;
return 0;
}
cout << "YES" << endl;
for (int i = m; i>=1; --i) cout << arr[i] << (i==1 ? '\n':' ');
return 0;
}
求补图连通块个数
CodeForces 1242B
const int maxn = 2e5+10;
const int maxm = 1e5+10;
int n, m;
bool vis[maxn];
set<int> st, e[maxn];
void bfs(int u) {
queue<int> q;
q.push(u);
st.erase(u);
vis[u] = 1;
while(!q.empty()) {
int t = q.front(); q.pop();
auto it = st.begin();
while(it!=st.end()) {
int v = *it++;
if (!e[v].count(t)) { //该点在删去的边中找不到,说明一定是补图中的点
st.erase(v);
q.push(v);
vis[v] = 1;
}
}
}
}
int main(){
cin >> n >> m;
int ans = 0;
for (int i = 1, a, b; i<=m; ++i) {
cin >> a >> b;
e[a].insert(b);
e[b].insert(a);
}
for (int i = 1; i<=n; ++i) st.insert(i);
int cnt = 0;
for (int i = 1; i<=n; ++i)
if (!vis[i]) {
++cnt;
bfs(i); //每次将一个补图中的连通块消去
}
cout << cnt-1 << endl;
return 0;
}
最短路
spfa
Acwing 340 可以有k条免费的最短路
const int maxn = 1e3+10;
const int maxm = 1e6+10;
struct E {
int to, w, nxt;
} e[maxm]; int h[maxn], tot;
void add(int u, int v, int w) {
e[++tot] = {v, w, h[u]}; h[u] = tot;
}
int n, m, k, vis[maxn], d[maxn][maxn];
void spfa() {
clr(d, 0x3f); clr(vis, 0);
queue<int> q; q.push(1); d[1][0] = 0;
while(!q.empty()) {
int u = q.front(); q.pop(); vis[u] = 0;
for (int i = h[u]; i; i=e[i].nxt) {
int v = e[i].to;
for (int j = 0; j<=k; ++j) {
int w = max(d[u][j], e[i].w);
if (j) w = min(d[u][j-1], w);
if (d[v][j]>w) {
d[v][j] = w;
if (!vis[v]) vis[v] = 1, q.push(v);
}
}
}
}
}
int main() {
cin >> n >> m >> k; tot = 0;
for (int i = 0; i<=n; ++i) h[i] = 0;
for (int i = 0,u,v,w; i<m; ++i) {
scanf("%d%d%d", &u, &v, &w);
add(u, v, w), add(v, u, w);
}
spfa();
int ans = INF;
for (int i = 0; i<=n; ++i) ans = min(ans, d[n][i]);
if (ans==INF) ans = -1;
cout << ans << endl;
return 0;
}
acwing1165 负环+01分数规划
const int maxn = 1e3+10;
const int maxm = 1e6+10;
int n;
vector<P> e[maxn];
int vis[maxn], cnt[maxn];
double d[maxn];
int check(double x) {
stack<int> sk;
for (int i = 1; i<=710; ++i) sk.push(i), vis[i] = 0, d[i] = 0, cnt[i] = 1;
int c = 0;
while(!sk.empty()) {
int u = sk.top(); sk.pop(); //判负环栈快一点
++c;
if (c>=10000) return 1; //trick 效率很低的时候大概率有负环
vis[u] = 0;
for (auto node : e[u]) {
int v = node.y;
double w = node.x;
if (d[v]<d[u]+w-x) {
d[v] = d[u]+w-x;
cnt[v] = cnt[u]+1;
if (cnt[v]>710) return 1;
if (!vis[v]) {
vis[v] = 1;
sk.push(v);
}
}
}
}
return 0;
}
int main(void) {
IOS;
while(cin >> n && n) {
for (int i = 1; i<=n; ++i) {
string s; cin >> s;
int len = s.size();
if (len<2) continue; // 题目建图要求
int a = (s[0]-'a'+1)*26+s[1]-'a'+1;
int b = (s[len-2]-'a'+1)*26+s[len-1]-'a'+1;
e[a].push_back({len, b});
}
double l = 0, r = 1000; //01分数规划
for (int i = 1; i<=50; ++i) {
double mid = (l+r)/2;
if (check(mid)) l = mid;
else r = mid;
}
if (l<=eps) cout << "No solution" << endl;
else cout << fixed << setprecision(3) << l << endl;
for (int i = 1; i<=710; ++i) e[i].clear();
}
return 0;
}
dijkstra
AcWing 342含有正的双向边和负的单向边的单源最短路(卡spfa)
const int maxn = 2e5+10;
vector<P> e[maxn];
int n, m1, m2, s, in[maxn];
int tot, vis[maxn], d[maxn], num[maxn];
vector<int> g[maxn];
void dfs(int u) {
g[tot].push_back(u);
num[u] = tot;
for (auto node : e[u]) {
int v = node.y;
if (num[v]) continue;
dfs(v);
}
}
queue<int> q;
void dij(int u) {
priority_queue<P, vector<P>, greater<P> > pq;
for (auto v : g[u]) pq.push({d[v], v});
while(!pq.empty()) {
int u = pq.top().y; pq.pop();
if (vis[u]) continue;
vis[u] = 1;
for (auto node : e[u]) {
int v = node.y;
int w = node.x;
if (d[u]!=INF && d[v]>d[u]+w) {
d[v] = d[u]+w;
if (num[u]==num[v]) pq.push({d[v], v});
}
if (num[u]!=num[v] && --in[num[v]]==0) q.push(num[v]);
}
}
}
void topo() {
q.push(s);
for (int i = 1; i<=tot; ++i)
if (!in[i]) q.push(i);
while(!q.empty()) {
int u = q.front(); q.pop();
dij(u);
}
}
int main() {
IOS;
cin >> n >> m1 >> m2 >> s;
for (int i = 1, a, b, c; i<=m1; ++i) {
cin >> a >> b >> c;
e[a].push_back({c, b});
e[b].push_back({c, a});
}
for (int i = 1; i<=n; ++i)
if (!num[i]) ++tot, dfs(i);
for (int i = 1, a, b, c; i<=m2; ++i) {
cin >> a >> b >> c;
e[a].push_back({c, b});
++in[num[b]];
}
clr(d, 0x3f); d[s] = 0;
topo();
for (int i = 1; i<=n; ++i) {
if (d[i]==INF) cout << "NO PATH" << endl;
else cout << d[i] << endl;
}
return 0;
}
floyed
AcWing344 最少包含三个边的最短路,且输出路径
const int maxn = 3e2+10;
const int maxm = 1e4+10;
int res[maxn][maxn], g[maxn][maxn];
int n, m, p[maxn][maxn];
vector<int> path;
void solve(int u, int v) {
if (!p[u][v]) return;
solve(u, p[u][v]);
path.push_back(p[u][v]);
solve(p[u][v], v);
}
int main(void) {
clr(g, 0x3f);
cin >> n >> m;
for (int i = 0, a, b, c; i<m; ++i) {
cin >> a >> b >> c;
g[a][b] = g[b][a] = min(g[a][b], c);
}
memcpy(res, g, sizeof(g));
ll ans = LLONG_MAX;
for (int k = 1; k<=n; ++k) {
for (int i = 1; i<=n; ++i)
for (int j = i+1; j<=n; ++j)
if (i!=j && i!=k && j!=k && ans>(ll)res[i][j]+g[j][k]+g[k][i]) {
ans = (ll)res[i][j]+g[j][k]+g[k][i];
path.clear();
path.push_back(i);
solve(i, j);
path.push_back(j);
path.push_back(k);
}
for (int i = 1; i<=n; ++i)
for (int j = 1; j<=n; ++j)
if (res[i][j]>res[i][k]+res[k][j]) p[i][j] = k, res[i][j] = res[i][k]+res[k][j];
}
if (ans>=INF) cout << "No solution." << endl;
else {
int sz = path.size();
for (int i = 0; i<sz; ++i) printf(i==sz-1?"%d\n":"%d ", path[i]);
}
return 0;
}
非递归存储路径
const int maxn = 1e2+10;
const int maxm = 1e6+10;
int n, m;
ll g[maxn][maxn], d[maxn][maxn], f[maxn][maxn];
int pth[maxn][maxn];
int main(void) {
IOS;
cin >> n >> m;
ll ans = 1e18;
for (int i = 1; i<=n; ++i)
for (int j = 1; j<=n; ++j) {
if (i==j) d[i][j] = g[i][j] = 0;
else d[i][j] = g[i][j] = 1e18;
}
for (int i = 1, a, b, c; i<=m; ++i) {
cin >> a >> b >> c;
d[a][b] = d[b][a] = g[a][b] = g[b][a] = min(g[a][b], 1LL*c);
}
for (int i = 1; i<=n; ++i)
for (int j = 1; j<=n; ++j)
pth[i][j] = j;
int x, y, z;
vector<int> anss;
for (int k = 1; k<=n; ++k) {
for (int i = 1; i<=n; ++i)
for (int j = i+1; j<=n; ++j) {
if (i!=k && j!=k && d[i][j]+g[i][k]+g[k][j]<ans) {
ans = d[i][j]+g[i][k]+g[k][j];
x = i, y = j, z = k;
anss.clear();
anss.push_back(x);
while(x!=y) {
anss.push_back(pth[x][y]);
x = pth[x][y];
}
anss.push_back(z);
}
}
for (int i = 1; i<=n; ++i)
for (int j = 1; j<=n; ++j) {
if (d[i][j]>d[i][k]+d[k][j]) {
d[i][j] = d[i][k]+d[k][j];
f[i][j] = k;
pth[i][j] = pth[i][k];
}
}
}
if (ans>=1e18-2) cout << "No solution." << endl;
else {
for (auto v : anss) cout << ' ' << v ;
cout << endl;
}
return 0;
}
AcWing 345恰好k条边,可以重复的最短路
const int maxn = 2e2+10;
const int maxm = 1e6+10;
int n, t, s, e, tot;
map<int, int> mp;
ll g[maxn][maxn], ans[maxn][maxn], tmp[maxn][maxn];
void mul(ll a[maxn][maxn], ll b[maxn][maxn]) {
clr(tmp, 0x3f);
for (int i = 1; i<=tot; ++i)
for (int j = 1; j<=tot; ++j)
for (int k = 1; k<=tot; ++k)
if (tmp[j][k]>a[j][i]+b[i][k]) tmp[j][k]=a[j][i]+b[i][k];
memcpy(a, tmp, sizeof(tmp));
}
int main() {
cin >> n >> t >> s >> e;
clr(g, 0x3f);
for (int i = 1, a, b, c; i<=t; ++i) {
cin >> c >> a >> b;
if (!mp[a]) mp[a] = ++tot;
if (!mp[b]) mp[b] = ++tot;
g[mp[a]][mp[b]] = g[mp[b]][mp[a]] = min(g[mp[a]][mp[b]], (ll)c);
}
clr(ans, 0x3f);
for (int i = 1; i<=tot; ++i) ans[i][i] = 0;
while(n) {
if (n&1) mul(ans, g);
mul(g, g);
n >>= 1;
}
cout << ans[mp[s]][mp[e]] << endl;
return 0;
}
次短路
AcWing 383. 观光 最短路与距离差1的次短路计数
const int maxn = 1e6+10;
int n, m, s, t;
int d[maxn][2]; ll cnt[maxn][2];
bool vis[maxn][2];
struct INFO {
int x, y, i;
bool operator < (INFO a) const {
return x>a.x;
}
};
vector<P> e[maxn];
void dij() {
for (int i = 1; i<=n; ++i) {
d[i][1] = d[i][0] = INF;
cnt[i][1] = cnt[i][0] = 0;
vis[i][1] = vis[i][0] = 0;
}
priority_queue<INFO> pq;
pq.push({0, s, 0}); //一开始只放最短路的源点
d[s][0] = 0;
cnt[s][0] = 1;
while(!pq.empty()) {
INFO t = pq.top();
pq.pop();
if (vis[t.y][t.i]) continue;
vis[t.y][t.i] = 1;
for (auto node : e[t.y]) {
int v = node.y;
int w = node.x;
if (d[v][0]>d[t.y][t.i]+w) {
d[v][1] = d[v][0];
cnt[v][1] = cnt[v][0];
pq.push({d[v][1], v, 1});
//注意一条次短路可以由最短路+次短路更新过来,也可以由次短路+最短路更新过来
//所以松弛后的两种点都要加入优先队列中
d[v][0] = d[t.y][t.i]+w;
cnt[v][0] = cnt[t.y][t.i];
pq.push({d[v][0], v, 0});
}
else if (d[v][0]==d[t.y][t.i]+w) cnt[v][0] += cnt[t.y][t.i];
else if (d[v][1]>d[t.y][t.i]+w) {
d[v][1] = d[t.y][t.i]+w;
cnt[v][1] = cnt[t.y][t.i];
pq.push({d[v][1], v, 1});
}
else if (d[v][1]==d[t.y][t.i]+w) cnt[v][1] += cnt[t.y][t.i];
}
}
}
int main(void) {
IOS;
int __; cin >> __;
while(__--) {
cin >> n >> m;
for (int i = 1, a, b, c; i<=m; ++i) {
cin >> a >> b >> c;
e[a].push_back({c, b}); // 问题里是单向边
}
cin >> s >> t;
dij();
if (d[t][1]-d[t][0]==1) cnt[t][0] += cnt[t][1];
cout << cnt[t][0] << endl;
for (int i = 1; i<=n; ++i) e[i].clear();
}
return 0;
}
第k短路
const int maxn = 1e3+10;
const int maxm = 2e6+10;
struct E {
int to, w, nxt;
} e[maxm];
int tot, h[maxn], rh[maxn];
void add(int h[], int u, int v, int w) {
e[++tot] = {v, w, h[u]};
h[u] = tot;
}
int n, m, s, t, k;
int vis[maxn], d[maxn];
void dij() { //把终点到当前点的最短距离当作估价函数
clr(d, 0x3f); d[t] = 0;
priority_queue<P, vector<P>, greater<P> > pq;
pq.push({d[t], t});
while(!pq.empty()) {
int u = pq.top().y; pq.pop();
if (vis[u]) continue;
vis[u] = 1;
for (int i = rh[u]; i; i=e[i].nxt) {
int v = e[i].to;
if (d[v]>d[u]+e[i].w) {
d[v] = d[u]+e[i].w;
pq.push({d[v], v});
}
}
}
}
struct Node {
int w1, w2, u;
//按估计值排序
bool operator < (const Node a) const {
return w1>a.w1;
}
};
int astar() {
clr(vis, 0);
priority_queue<Node> pq;
pq.push({d[s], 0, s});
while(!pq.empty()) {
Node tt = pq.top(); pq.pop();
int u = tt.u, dis = tt.w2;
++vis[u]; //只有终点第k次弹出的时候是最优解,其他的点可能需要多次弹出
if (vis[t]==k) return dis;
for (int i = h[u]; i; i=e[i].nxt) {
int v = e[i].to;
if (vis[v]<k) pq.push({dis+e[i].w+d[v], dis+e[i].w, v});
}
}
return -1;
}
int main() {
IOS;
cin >> n >> m;
for (int i = 1, a, b, c; i<=m; ++i) {
cin >> a >> b >> c;
add(h, a, b, c);
add(rh, b, a, c);
}
cin >> s >> t >> k;
dij();
if (s==t) ++k;
cout << astar() << endl;
return 0;
}
差分约束
acwing1170 差分约束+判负环
const int maxn = 1e3+10;
const int maxm = 1e6+10;
struct E {
int to, w, nxt;
} e[maxm];
int h[maxn], tot;
void add(int u, int v, int w) {
++tot;
e[tot].to = v;
e[tot].w = w;
e[tot].nxt = h[u];
h[u] = tot;
}
int n, ml, md, cnt[maxn], d[maxn], vis[maxn];
int spfa(int sz) {
clr(vis, 0);
clr(d, 0x3f);
clr(cnt, 0);
queue<int> q;
for (int i = 1; i<=sz; ++i) {
d[i] = 0;
vis[i] = 0;
q.push(i);
}
while(!q.empty()) {
int u = q.front(); q.pop();
vis[u] = 0;
for (int i = h[u]; i; i = e[i].nxt) {
int v = e[i].to, w = e[i].w;
if (d[v]>d[u]+w) {
d[v] = d[u]+w;
cnt[v] = cnt[u]+1;
if (cnt[v]>=n) return 1;
if (!vis[v]) {
vis[v] = 1;
q.push(v);
}
}
}
}
return 0;
}
//a-b<=c,求最小值,最小上届,求上届最长路
//a-b>=c, 求最大值,最大下届,求下届最短路
int main() {
cin >> n >> ml >> md;
for (int i = 1, a, b, c; i<=ml; ++i) {
cin >> a >> b >> c;
if (a>b) swap(a, b);
add(a, b, c); //b-a<=c -> a+c>=b
}
for (int i = 1, a, b, c; i<=md; ++i) {
cin >> a >> b >> c;
if (a>b) swap(a, b);
add(b, a, -c); //b-a<=c -> b-c>=a
}
for (int i = 1; i<n; ++i) add(i+1, i, 0);
if (spfa(n)) cout << -1 << endl;
else {
spfa(1);
if (d[n]==INF) cout << -2 << endl;
else cout << d[n] << endl;
}
return 0;
}
kruskal重构树
bzoj 3732 给你一张无向图,每次询问从A点走到B点的所有路径中,最长的边最小值是多少?
按最小生成树建kruskal重构树,用新加的点的点权代表两点间的边权,由于满足kruskal重构树满足堆的性质,故lca(A,B)对应的边权即为答案。
const int maxn = 2e5+10;
const int maxm = 2e5+10;
int n, m, k;
struct E {
int u, v, w;
} e[maxm];
vector<int> g[maxn];
int p[maxn], val[maxn], tot, f[maxn][20];
int find(int x) {
return p[x]==x ? p[x]:p[x]=find(p[x]);
}
int dep[maxn];
void dfs(int u) {
for (auto v : g[u]) {
dep[v] = dep[u]+1;
f[v][0] = u;
for (int i = 1; i<20; ++i) f[v][i] = f[f[v][i-1]][i-1];
dfs(v);
}
}
int lca(int u, int v) {
if (dep[u]<dep[v]) swap(u, v);
for (int i = 19; i>=0; --i)
if (dep[f[u][i]]>=dep[v]) u = f[u][i];
if (u==v) return u;
for (int i = 19; i>=0; --i)
if (f[u][i]!=f[v][i]) u = f[u][i], v = f[v][i];
return f[u][0];
}
int main() {
IOS;
cin >> n >> m >> k;
for (int i = 1; i<=m; ++i) cin >> e[i].u >> e[i].v >> e[i].w;
sort(e+1, e+m+1, [](E a, E b) {return a.w<b.w;});
for (int i = 1; i<=2*n; ++i) p[i] = i;
tot = n;
for (int i = 1; i<=m; ++i) {
int fa = find(e[i].u);
int fb = find(e[i].v);
if (fa!=fb) {
++tot;
p[fa] = tot;
p[fb] = tot;
val[tot] = e[i].w;
g[tot].push_back(fa);
g[tot].push_back(fb);
}
}
dep[tot] = 1;
dfs(tot);
while(k--) {
int a, b; cin >> a >> b;
cout << val[lca(a, b)] << endl;
}
return 0;
}
次小生成树
const int maxn = 1e5+10;
const int maxm = 1e6+10;
struct G {
int u, v, w;
} g[maxm];
int n, m, p[maxn];
int find(int x) {
return p[x]==x ? p[x]:p[x]=find(p[x]);
}
struct E {
int to, w, nxt;
} e[maxm];
int h[maxn], tot;
inline void add(int u, int v, int w) {
e[++tot] = {v, w, h[u]};
h[u] = tot;
}
bool vis[maxm];
ll kruskal() {
for (int i = 1; i<=n; ++i) p[i] = i;
ll sum = 0;
for (int i = 1; i<=m; ++i) {
int fa = find(g[i].u);
int fb = find(g[i].v);
if (fa!=fb) {
vis[i] = 1;
p[fa] = fb;
sum += g[i].w;
add(g[i].u, g[i].v, g[i].w);
add(g[i].v, g[i].u, g[i].w);
}
}
return sum;
}
int dep[maxn], f[maxn][21], dm1[maxn][21], dm2[maxn][21];
void bfs() {
queue<int> q; q.push(1);
dep[1] = 1;
while(!q.empty()) {
int u = q.front(); q.pop();
for (int i = h[u]; i; i=e[i].nxt) {
int v = e[i].to;
if (dep[v]) continue;
dep[v] = dep[u]+1;
q.push(v);
f[v][0] = u;
for (int j = 1; j<21; ++j) f[v][j] = f[f[v][j-1]][j-1];
dm1[v][0] = e[i].w, dm2[v][0] = -INF;
for (int j = 1; j<21; ++j) {
int dist[2] = {dm1[f[v][j-1]][j-1], dm2[f[v][j-1]][j-1]};
dm1[v][j] = dm1[v][j-1];
dm2[v][j] = dm2[v][j-1];
for (int k = 0; k<2; ++k) {
int d = dist[k];
if (d>dm1[v][j]) dm2[v][j] = dm1[v][j], dm1[v][j] = d;
else if (d<dm1[v][j] && d>dm2[v][j]) dm2[v][j] = d;
}
}
}
}
}
inline int gm(int x, int i, int w) {
int d = -INF;
if (w>dm1[x][i]) d = max(d, dm1[x][i]);
//因为dm2<dm1,所以当w<=dm1的时候,即使w等于dm1,也不会等于dm2
else d = max(d, dm2[x][i]);
return d;
}
int lca(int x, int y, int w) {
if (dep[x]<dep[y]) swap(x, y);
int d = -INF;
for (int i = 20; i>=0; --i)
if (dep[f[x][i]]>=dep[y]) {
d = max(d, gm(x, i, w));
x = f[x][i];
}
if (x==y) return d;
for (int i = 20; i>=0; --i)
if (f[x][i]!=f[y][i]) {
d = max(d, gm(x, i, w));
d = max(d, gm(y, i, w));
x = f[x][i];
y = f[y][i];
}
d = max(d, gm(x, 0, w));
d = max(d, gm(y, 0, w));
return d;
}
int main() {
IOS; cin >> n >> m;
for (int i = 1; i<=m; ++i) cin >> g[i].u >> g[i].v >> g[i].w;
sort(g+1, g+m+1, [](G a, G b) {return a.w<b.w;});
ll sum = kruskal(); //求最小生成树然后标记原图中的边
bfs(); //倍增求每个点向上跳2^i步的最大值与次大值
ll ans = 1e18;
for (int i = 1; i<=m; ++i) {
if (vis[i]) continue;
/*枚举删去最小生成树的一条边,然后在两点与lca形成的路径中找一条比
删去的边权值小的最大的边*/
ans = min(ans, sum+g[i].w-lca(g[i].u, g[i].v, g[i].w));
}
cout << ans << endl;
return 0;
}
LCA
倍增
const int maxn = 1e5+10;
const int maxm = 2e6+10;
struct E {int to, nxt, w;} e[maxm]; int h[maxn], tot;
void add(int u, int v, int w) {e[++tot] = {v, h[u], w}, h[u] = tot;}
int n, m, f[maxn][21], d[maxn]; ll dis[maxn];
void bfs(int x) {
d[x] = 1, dis[x] = 0;
queue<int> q; q.push(x);
while(!q.empty()) {
int u = q.front(); q.pop();
for (int i = h[u]; i; i = e[i].nxt) {
int v = e[i].to;
if (d[v]) continue;
d[v] = d[u]+1;
dis[v] = dis[u]+e[i].w;
q.push(v);
f[v][0] = u;
for (int j = 1; j<=20; ++j) f[v][j] = f[f[v][j-1]][j-1];
}
}
}
int lca(int x, int y) {
if (d[x]>d[y]) swap(x, y);
for (int i = 20; i>=0; --i)
if (d[f[y][i]]>=d[x]) y = f[y][i];
if (x==y) return x;
for (int i = 20; i>=0; --i)
if (f[x][i]!=f[y][i]) x = f[x][i], y = f[y][i];
return f[x][0];
}
int main(void) {
int T; cin >> T;
while(T--) {
cin >> n >> m; tot = 0;
clr(h, 0); clr(d, 0); clr(f, 0);
for (int i = 0, a, b, c; i<n-1; ++i) {
scanf("%d%d%d", &a, &b, &c);
add(a, b, c), add(b, a, c);
}
bfs(1);
for (int i = 0, a, b; i<m; ++i) {
scanf("%d%d", &a, &b);
printf("%lld\n", dis[a]+dis[b]-2*dis[lca(a,b)]);
}
}
return 0;
}
tarjan
const int maxn = 1e5+10;
const int maxm = 2e6+10;
struct E {
int to, nxt, w;
} e[maxm]; int h[maxn], tot;
void add(int u, int v, int w) {
e[++tot] = {v, h[u], w}; h[u] = tot;
}
vector<P> quary[maxn];
int n, m, d[maxn], ans[maxn], state[maxn], p[maxn];
void dfs(int u, int p) {
for (int i = h[u]; i; i=e[i].nxt) {
int v = e[i].to;
if (v!=p) d[v] = d[u]+e[i].w, dfs(v, u);
}
}
int find(int x) {
return p[x]==x ? p[x]:p[x]=find(p[x]);
}
void tarjan(int u, int fa) {
state[u] = 1;
for (int i = h[u]; i; i=e[i].nxt) {
int v = e[i].to;
if (v==fa) continue;
if (!state[v]) tarjan(v, u);
p[v] = u;
}
for (auto t : quary[u]) {
int v = t.second, id = t.first;
if (state[v]==2) ans[id] = d[u]+d[v]-d[find(v)]*2;
}
state[u] = 2;
}
int main(void) {
int t; cin >> t;
while(t--) {
cin >> n >> m; tot = 0;
for (int i = 0, a, b, c; i<n-1; ++i) {
scanf("%d%d%d", &a, &b, &c);
add(a, b, c), add(b, a, c);
}
for (int i = 1, a, b; i<=m; ++i) {
scanf("%d%d", &a, &b);
quary[a].push_back({i,b}), quary[b].push_back({i,a});
ans[i] = INF;
}
for (int i = 1; i<=n; ++i) d[i] = INF, p[i] = i;
d[1] = 0; dfs(1, 0);
tarjan(1, -1);
for (int i = 1; i<=m; ++i) printf("%d\n", ans[i]), quary[i].clear();
for (int i = 1; i<=n; ++i) state[i] = 0, ans[i] = 0, h[i] = 0;
}
return 0;
}
强联通分量
void tarjan(int u) {
dfn[u] = low[u] = ++__dfn;
sk[++tp] = u;
for (int i = h[u]; i; i=e[i].nxt) {
int v = e[i].to;
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
}
else if (!id[v]) low[u] = min(low[u], dfn[v]);
}
if (low[u]==dfn[u]) {
int v;
++scc;
do {
v = sk[tp--];
s[scc].push_back(v);
id[v] = scc;
++num[scc];
} while(v!=u);
}
}
AcWing 1175. 最大半连通子图+计数
const int maxn = 1e5+10;
int n, m, x;
struct E {
int to, nxt;
} e[maxn*20];
int h[maxn], tot;
void add(int u, int v) {
e[++tot] = {v, h[u]};
h[u] = tot;
}
int dfn[maxn], __dfn, low[maxn];
vector<int> s[maxn];
int scc, num[maxn];
int sk[maxn], tp, id[maxn];
int dp1[maxn], dp2[maxn];
set<ll> st;
void tarjan(int u) {
dfn[u] = low[u] = ++__dfn;
sk[++tp] = u;
for (int i = h[u]; i; i=e[i].nxt) {
int v = e[i].to;
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
}
else if (!id[v]) low[u] = min(low[u], dfn[v]);
}
if (low[u]==dfn[u]) {
int v;
++scc;
do {
v = sk[tp--];
s[scc].push_back(v);
id[v] = scc;
++num[scc];
} while(v!=u);
}
}
int main(void) {
IOS;
cin >> n >> m >> x;
for (int i = 1, a, b; i<=m; ++i) {
cin >> a >> b;
add(a, b);
}
for (int i = 1; i<=n; ++i)
if (!dfn[i]) tarjan(i);
//隐式建图,所有scc编号的逆序即拓扑序
for (int i = scc; i>=1; --i) {
if (dp1[i]==0) dp1[i] = num[i], dp2[i] = 1;
for (auto u : s[i])
for (int j = h[u]; j; j=e[j].nxt) {
int v = e[j].to;
if (id[u]!=id[v] && !st.count(1LL*u*100000011+v)) {
st.insert(1LL*u*100000011+v); //判断重边
int uu = id[u], vv = id[v];
if (dp1[vv]<dp1[uu]+num[vv]) {
dp1[vv] = dp1[uu]+num[vv];
dp2[vv] = dp2[uu];
}
else if (dp1[vv]==dp1[uu]+num[vv]) {
dp2[vv] = (dp2[vv]+dp2[uu])%x;
}
}
}
}
int maxx = -1, sum = 0;
for (int i = 1; i<=scc; ++i) {
if (dp1[i]>maxx) {
maxx = dp1[i];
sum = dp2[i];
}
else if (dp1[i]==maxx) {
sum += dp2[i];
}
//cout << dp1[i] << ' ' << dp2[i] << endl;
}
cout << maxx << endl;
cout << sum << endl;
return 0;
}
边双连通分量
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++__dfn;
sk[++tp] = u;
for (int i = h[u]; i; i=e[i].nxt) {
if ((fa^1)==i) continue;
int v = e[i].to;
if (!dfn[v]) {
tarjan(v, i);
low[u] = min(low[u], low[v]);
if (low[v]>dfn[u]) isbrige[i] = isbrige[i^1] = 1;
}
else low[u] = min(low[u], dfn[v]);
}
if (low[u]==dfn[u]) {
int v;
++dcc;
do {
v = sk[tp--];
id[v] = dcc;
} while(v!=u);
}
}
AcWing 395. 一个无向图添加多少边可以变成一个边双连通分量
const int maxn = 1e6+10;
struct E {
int to, nxt;
} e[maxn];
int h[maxn], tot = 1;
void add(int u, int v) {
e[++tot] = {v, h[u]};
h[u] = tot;
}
int n, m;
int dfn[maxn], low[maxn], __dfn;
int sk[maxn], tp, dcc, id[maxn];
int isbrige[maxn], out[maxn];
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++__dfn;
sk[++tp] = u;
for (int i = h[u]; i; i=e[i].nxt) {
if ((fa^1)==i) continue;
int v = e[i].to;
if (!dfn[v]) {
tarjan(v, i);
low[u] = min(low[u], low[v]);
if (low[v]>dfn[u]) isbrige[i] = isbrige[i^1] = 1;
}
else low[u] = min(low[u], dfn[v]);
}
if (low[u]==dfn[u]) {
int v;
++dcc;
do {
v = sk[tp--];
id[v] = dcc;
} while(v!=u);
}
}
int main(void) {
IOS;
cin >> n >> m;
for (int i = 1, a, b; i<=m; ++i) {
cin >> a >> b;
add(a, b);
add(b, a);
}
tarjan(1, -1);
for (int i = 1; i<=tot; ++i)
if (isbrige[i]) ++out[id[e[i].to]];
int cnt = 0;
for (int i = 1; i<=dcc; ++i)
if (out[i]==1) ++cnt;
cout << (cnt+1)/2 << endl;
return 0;
}
点双连通分量
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++__dfn;
sk[++tp] = u;
if (u==rt && !h[u]) {
++__dcc;
dcc[__dcc].push_back(u);
return;
}
int cnt = 0;
for (int i = h[u]; i; i=e[i].nxt) {
//if ((fa^1)==i) continue;
int v = e[i].to;
if (!dfn[v]) {
tarjan(v, i);
low[u] = min(low[u], low[v]);
if (low[v]>=dfn[u]) {
++cnt;
if (u!=rt || cnt>1) cut[u] = 1;
int t;
++__dcc;
do {
t = sk[tp--];
dcc[__dcc].push_back(t);
} while(t!=v); //注意, 这里是t!=v, 而不是t!=u
dcc[__dcc].push_back(u); //注意, 这里是u
}
}
else low[u] = min(low[u], dfn[v]);
}
}
AcWing 396 需要设置几个特殊点使得删除某特殊个点之后其他的点都能与剩下的特殊点连通
const int maxn = 1e3+10;
struct E {
int to, nxt;
} e[maxn];
int h[maxn], tot;
void add(int u, int v) {
e[++tot] = {v, h[u]};
h[u] = tot;
}
int n, m, rt;
int dfn[maxn], low[maxn], __dfn;
vector<int> dcc[maxn];
int sk[maxn], tp, __dcc, cut[maxn];
void init() {
clr(h, 0);
clr(cut, 0);
clr(dfn, 0);
for (int i = 1; i<=1000; ++i) dcc[i].clear(), h[i] = 0;
tot = 1; __dcc = tp = m = 0;
}
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++__dfn;
sk[++tp] = u;
if (u==rt && !h[u]) {
++__dcc;
dcc[__dcc].push_back(u);
return;
}
int cnt = 0;
for (int i = h[u]; i; i=e[i].nxt) {
//if ((fa^1)==i) continue;
int v = e[i].to;
if (!dfn[v]) {
tarjan(v, i);
low[u] = min(low[u], low[v]);
if (low[v]>=dfn[u]) {
++cnt;
if (u!=rt || cnt>1) cut[u] = 1;
int t;
++__dcc;
do {
t = sk[tp--];
dcc[__dcc].push_back(t);
} while(t!=v); //注意, 这里是t!=v, 而不是t!=u
dcc[__dcc].push_back(u); //注意, 这里是u
}
}
else low[u] = min(low[u], dfn[v]);
}
}
int main(void) {
IOS; int kkk = 0;
while(cin >> n && n) {
init();
for (int i = 1, a, b; i<=n; ++i) {
cin >> a >> b;
add(a, b);
add(b, a);
m = max(m, max(a, b));
}
for (int i = 1; i<=m; ++i)
if (!dfn[i]) tarjan(rt = i, -1);
ull ans = 1; int num = 0;
for (int i = 1; i<=__dcc; ++i) {
int cnt = 0;
for (auto v : dcc[i])
if (cut[v]) ++cnt;
if (dcc[i].size()==1) ++num;
else if (cnt==0) ans *= 1LL*dcc[i].size()*(dcc[i].size()-1)/2, num += 2;
else if (cnt==1) ans *= dcc[i].size()-cnt, ++num;
}
cout << "Case " << ++kkk << ": " << num << ' ' << ans << endl;
}
return 0;
}
二分图匹配
匈牙利算法
int n, m, k;
int find(int x) {
for (int i = 1; i<=m; ++i)
if (mp[x][i] && !vis[i]) {
vis[i] = true;
if (!match[i] || find(match[i])) {
match[i] = x; return 1;
}
}
return 0;
}
int solve() {
int ans = 0;
for (int i = 1; i<=n; ++i)
if (find(i)) ++ans;
return ans;
}
km算法
const int maxn = 1e2+10;
const int maxm = 30;
int match[maxn], lx[maxn], ly[maxn], s[maxn];
int visx[maxn], visy[maxn], pre[maxn];
int n, m, g[maxn][maxn];
void find(int k) {
int y = 0, p = 0; clr(pre, 0);
for (int i = 1; i<=m; ++i) s[i] = INF;
match[y] = k;
while(1) {
int x = match[y], d = INF; visy[y] = 1;
for (int i = 1; i<=m; ++i)
if (!visy[i]) {
if (s[i] > lx[x]+ly[i]-g[x][i])
s[i] = lx[x]+ly[i]-g[x][i], pre[i] = y;
if (d > s[i]) d = s[i], p = i;
}
for (int i = 0; i<=m; ++i) {
if (visy[i]) lx[match[i]] -= d, ly[i] += d;
else s[i] -= d;
}
y = p;
if (!match[y]) break;
}
while(y) match[y] = match[pre[y]], y = pre[y];
}
int km() {
clr(lx, 0x3f); clr(ly, 0); clr(match, 0);
for (int i = 1; i<=n; ++i)
clr(visy, 0), find(i);
int ans = 0;
for (int i = 1; i<=m; ++i) ans += g[match[i]][i];
return ans;
}
动态规划
线性dp
AcWing 1052 dp+kmp, 求不包含子串t的长度为n的字符串数量
const int maxn = 1e2+10;
const int maxm = 3e4+10;
char str[maxn];
int nxt[maxn], f[maxn][maxn];
ll dp[maxn][maxn];
void get_nxt() {
int i = 1, j = 0;
nxt[i] = j;
int len = strlen(str+1);
while(i<len) {
while(j && str[j]!=str[i]) j = nxt[j];
nxt[++i] = ++j;
}
}
int main() {
IOS;
int n; cin >> n;
cin >> str+1;
get_nxt();
for (int i = 0; i<n; ++i) {
for (char c = 'a'; c<='z'; ++c) {
int j = i+1;
while(j && str[j]!=c) j = nxt[j];
f[i][c-'a'] = j;
//匹配长度为i时下一个字符放c能够匹配的长度
}
}
dp[0][0] = 1; //一开始的匹配长度为0
int len = strlen(str+1);
for (int i = 0; i<=n; ++i)
for (int j = 0; j<len; ++j)
for (int k = 0; k<26; ++k)
dp[i+1][f[j][k]] = (dp[i+1][f[j][k]]+dp[i][j])%MOD;
ll ans = 0;
for (int i = 0; i<len; ++i) ans = (ans+dp[n][i])%MOD;
cout << ans << endl;
return 0;
}
AcWing 1053 dp+ac自动机, 求修改给出的字符串使其不包含所有给出的字符串的最小修改次数
const int maxn = 1e3+10;
const int maxm = 3e4+10;
char str[maxn];
int n, to[maxn];
int tr[maxn][4], idx, dar[maxn], fail[maxn];
void insert() {
int p = 0;
for (int i = 1; str[i]; ++i) {
int t = to[str[i]];
if (!tr[p][t]) tr[p][t] = ++idx;
p = tr[p][t];
}
dar[p] = 1;
}
int q[maxn];
void build() {
int hh = 0, tt = -1;
for (int i = 0; i<4; ++i)
if (tr[0][i]) q[++tt] = tr[0][i];
while(hh<=tt) {
int t = q[hh++];
for (int i = 0; i<4; ++i) {
int p = tr[t][i];
if (!p) tr[t][i] = tr[fail[t]][i];
else {
fail[p] = tr[fail[t]][i];
dar[p] |= dar[fail[p]]; //如果后缀有匹配串,把它的后缀也标记上
q[++tt] = p;
}
}
}
}
int dp[maxn][maxn];
int main() {
IOS;
int kase = 0;
to['A'] = 0, to['T'] = 1, to['C'] = 2, to['G'] = 3;
while(cin >> n && n) {
idx = 0;
clr(tr, 0);
clr(dar, 0);
clr(fail, 0);
for (int i = 1; i<=n; ++i) {
cin >> str+1;
insert();
}
build();
cin >> str+1;
clr(dp, 0x3f);
dp[0][0] = 0; //一开始没有匹配ac自动机的任何位置
int len = strlen(str+1);
for (int i = 0; i<len; ++i)
for (int j = 0; j<=idx; ++j)
for (int k = 0; k<4; ++k) {
int t = to[str[i+1]] != k;
int p = tr[j][k];
if (!dar[p]) dp[i+1][p] = min(dp[i+1][p], dp[i][j]+t);
}
int res = 0x3f3f3f3f;
for (int i = 0; i<=idx; ++i) res = min(res, dp[len][i]);
if (res == 0x3f3f3f3f) res = -1;
cout << "Case " << ++kase << ": " << res << endl;
}
return 0;
}
sos dp
codeforces 165E 给你n个数,对于每个数,让你找一个其他的数字与这个数异或为0
从二进制的角度考虑,两个数异或为0,即两个数的二进制位没有交集,对于一个数来说,它的补集以及它的补集的子集必定和它没有交集,所以我们只要判断一个数字的补集的子集中有没有数组中存在的数就可以了,这里可以用sos dp解决。我们设dp[i]为补集的状态空间,将所有数字\(a_i\)视为一个补集初始化\(dp[a_i] = a_i\),然后求出所有状态的子集中的一个解即可。
const int maxn = 1e6+10;
const int maxm = 2e6+10;
int dp[1<<22], arr[maxn];
int main() {
IOS;
int n; cin >> n;
for (int i = 1; i<=n; ++i) cin >> arr[i];
int x = (1<<22)-1; clr(dp, 0xff);
for (int i = 1; i<=n; ++i) dp[arr[i]] = arr[i];
for (int i = 0; i<22; ++i)
for (int j = 0; j<(1<<22); ++j)
if ((j&(1<<i)) && dp[(j^(1<<i))]!=-1) dp[j] = dp[j^(1<<i)];
for (int i = 1; i<=n; ++i) cout << dp[arr[i]^x] << (i==n ? '\n':' ');
return 0;
}
概率dp
HDU 4035 树形概率dp递推一次函数
有一个树形的迷宫,从节点1开始走,每个节点都有\(k_i\)的概率回到1,\(e_i\)的概率逃出迷宫,每个房间有\(m\)条边相连,求走出迷宫所需步数的期望。
设走出迷宫步数的期望为\(E_i\),父亲为\(F_i\),儿子为\(S_i\),相邻的节点个数为\(m\),则\(E_1\)即为所求。
对于叶子节点来说,可以得到: \(E_i = k_i \times E_1 + (1-k_i-e_i) \times (1 + E_{F_i})\)。
即\(E_i = k_i \times E_1 + (1-k_i-e_i) \times E_{F_i} + 1-k_i-e_i\)。
对于非叶子节点来说,可以得到: \(E_i = k_i \times E_1 + \frac{(1-k_i-e_i)}{m} \times (1 + E_{F_i} + \sum (E_{S_i} + 1))\)。
即\(E_i = k_i \times E_1 + \frac{(1-k_i-e_i)}{m} \times E_{F_i} + \frac{(1-k_i-e_i)}{m} \times \sum E_{S_i} + 1-k_i-e_i\)。
我们发现每个式子中都有\(E_1\)这个变量,这是不便于我们递推的,我们可以尝试把递推的值转为一次函数。
设\(E_i = A_i \times E_1 + B_i \times E_{F_i} + C_i\), 那么将这个式带入非叶节点的公式替换掉\(E_{S_i}\)可得:
\(E_i = k_i \times E_1 + \frac{(1-k_i-e_i)}{m} \times E_{F_i} + \frac{(1-k_i-e_i)}{m} \times (\sum (A_{S_i} \times E_1 + B_{S_i} \times E_i + C_{S_i})) + 1-k_i-e_i\)
整理得: \((1 - \frac{(1-k_i-e_i)}{m} \times \sum B_{S_i}) \times E_i = (k_i + \frac{(1-k_i-e_i)}{m} \times \sum A_{S_i}) \times E_1 + \frac{(1-k_i-e_i)}{m} \times E_{F_i} + 1-k_i-e_i + \frac{(1-k_i-e_i)}{m} \times \sum C_{S_i}\)
\(A_i = (k_i + \frac{1-k_i-e_i}{m} \times \sum A_{S_i}) / (1 - \frac{1-k_i-e_i}{m} \times \sum B_{S_i})\)
\(B_i = (\frac {1-k_i-e_i}{m}) / (1 - \frac{1-k_i-e_i}{m} \times \sum B_{S_i})\)
\(C_i = (1-k_i-e_i + \frac {1-k_i-e_i}{m} \times \sum C_{S_i}) / (1 - \frac{1-k_i-e_i}{m} \times \sum B_{S_i})\)
这样我们通过递推出\(A_1, B_1, C_1\)就能得到答案了。
const int maxn = 1e5+10;
const int maxm = 2e6+10;
double k[maxn], e[maxn];
vector<int> g[maxn];
int n;
double a[maxn], b[maxn], c[maxn];
void init() {
clr(a, 0); clr(b, 0); clr(c, 0);
for (int i = 0; i<=n; ++i) g[i].clear();
}
bool dfs(int u, int p) {
double m = g[u].size();
double pi = (1-k[u]-e[u])/m;
double sum1 = k[u], sum2 = pi, sum3 = 1-k[u]-e[u], sum = 0;
for (auto v : g[u]) {
if (v==p) continue;
if (!dfs(v, u)) return 0;
sum1 += pi*a[v];
sum += pi*b[v];
sum3 += pi*c[v];
}
sum = 1-sum;
if (fabs(sum)<eps) return 0;
a[u] = sum1/sum;
b[u] = sum2/sum;
c[u] = sum3/sum;
return 1;
}
int main(void) {
//IOS;
int __; cin >> __;
int kase = 0;
while(__--) {
cin >> n;
init();
for (int i = 1; i<n; ++i) {
int a, b; scanf("%d%d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}
for (int i = 1; i<=n; ++i) {
scanf("%lf", &k[i]); k[i] /= 100.0;
scanf("%lf", &e[i]); e[i] /= 100.0;
}
if (dfs(1, -1) && fabs(1-a[1])>eps) printf("Case %d: %.6f\n", ++kase, c[1]/(1-a[1]));
else printf("Case %d: impossible\n", ++kase);
}
return 0;
}
bzoj2337 从1号点出发,任意点都可以随机走到其他点,走到n号点为止,问从1号点走到n号点的期望, 有重边和自环。
拆位高斯消元求概率dp。设f[i]表示从i异或到点n结果为1的概率,状态转移方程就是\(f[i] = \sum {f[v]/d[i]}(边权为0) + \sum{(1-f[v])/d[i]}(边权为1)\)。由于给的是无向图,所以转移的顺序不好确定,可以用高斯消元解出每位从点1到点n异或值为1的概率,结果乘上对应的二进制位权即是本位的期望。
const int maxn = 1e2+10;
const int maxm = 1e6+10;
int n, m, d[maxn];
vector<P> e[maxn];
double g[maxn][maxn];
void build(int x) {
clr(g, 0);
for (int i = 1; i<n; ++i) {
g[i][i] = d[i];
for (auto v : e[i]) {
if (v.x>>x&1) g[i][v.y] += 1.0, g[i][n+1] += 1.0;
else g[i][v.y] -= 1.0;
}
}
g[n][n] = 1;
}
void gauss() {
for (int r = 1, c = 1; c<=n; c++, r++) {
int t = r;
for (int i = r+1; i<=n; ++i)
if (fabs(g[i][c])-fabs(g[t][c])>1e-9) t = i;
for (int i = c; i<=n+1; ++i) swap(g[t][i], g[r][i]);
for (int i = n+1; i>=c; --i) g[r][i] /= g[r][c];
for (int i = r+1; i<=n; ++i)
for (int j = n+1; j>=c; --j)
g[i][j] -= g[i][c]*g[r][j];
}
for (int i = n; i>1; --i)
for (int j = i-1; j; --j) {
g[j][n+1] -= g[i][n+1]*g[j][i];
g[j][i] = 0;
}
}
int main() {
IOS;
cin >> n >> m;
for (int i = 1, a, b, c; i<=m; ++i) {
cin >> a >> b >> c;
e[a].push_back({c, b}), ++d[a];
if (a!=b) e[b].push_back({c, a}), ++d[b];
}
double sum = 0;
for (int i = 0; i<=30; ++i) {
build(i);
gauss();
sum += g[1][n+1]*(1<<i);
}
cout << fixed << setprecision(3) << sum << endl;
return 0;
}
虚树
bzoj2286 去掉几条边使无法从根到达给出的几个点,问最小花费
const int maxn = 5e5+10;
struct E {
int to, w, nxt;
} e[maxn];
int h[maxn], tot;
void add(int u, int v, int w) {
e[++tot] = {v, w, h[u]};
h[u] = tot;
}
ll minv[maxn], dis[maxn];
int dep[maxn], fa[maxn], sz[maxn], son[maxn];
int tim, ldfn[maxn], rdfn[maxn], vis[maxn];
void dfs1(int u, int p) {
ldfn[u] = ++tim; sz[u] = 1;
for (int i = h[u]; i; i=e[i].nxt) {
int v = e[i].to;
if (v==p) continue;
if (minv[u]>e[i].w) minv[v] = e[i].w;
else minv[v] = minv[u];
dep[v] = dep[u]+1;
dis[v] = dis[u]+e[i].w;
fa[v] = u;
dfs1(v, u);
sz[u] += sz[v];
if (sz[v]>sz[son[u]]) son[u] = v;
}
rdfn[u] = tim; //求出欧拉序用于判断父子关系
}
int top[maxn];
void dfs2(int u) {
if (u==son[fa[u]]) top[u] = top[fa[u]];
else top[u] = u;
for (int i = h[u]; i; i=e[i].nxt) {
int v = e[i].to;
if (v!=fa[u]) dfs2(v);
}
}
int lca(int u, int v) {
while(top[u]!=top[v]) {
if (dep[top[u]]>dep[top[v]]) u = fa[top[u]];
else v = fa[top[v]];
}
return dep[u]>dep[v]?v:u;
}
int n, m, k, d[maxn], sk[maxn];
void build() {
tot = 0; //注意
sort(d+1, d+k+1, [](int a, int b) {return ldfn[a]<ldfn[b];});
int keynum = k;
for (int i = 1; i<keynum; ++i) d[++k] = lca(d[i], d[i+1]);
sort(d+1, d+k+1, [](int a, int b) {return ldfn[a]<ldfn[b];});
k = unique(d+1, d+k+1)-d-1;
int tp = 1; sk[tp] = d[1];
for (int i = 2; i<=k; ++i) {
//欧拉序只要包含和完全不相交
while(tp && rdfn[sk[tp]]<ldfn[d[i]]) --tp;
//完全不相交说明栈顶和当前点无父子关系
if (tp) add(sk[tp], d[i], 0);
sk[++tp] = d[i];
}
}
ll dp[maxn];
void dfs3(int u) {
dp[u] = minv[u];
ll sum = 0;
for (int i = h[u]; i; i=e[i].nxt) {
int v = e[i].to;
dfs3(v);
sum += dp[v];
}
if (!vis[u]) dp[u] = min(dp[u], sum);
h[u] = 0, vis[u] = 0; //注意
}
int main() {
cin >> n;
clr(minv, 0x3f);
for (int i = 1, a, b, c; i<n; ++i) {
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
add(b, a, c);
}
dep[1] = 1;
dfs1(1, 0); dfs2(1);
clr(h, 0); tot = 0; //清空原树
cin >> m;
while(m--) {
scanf("%d", &k);
for (int i = 1; i<=k; ++i) scanf("%d", &d[i]);
for (int i = 1; i<=k; ++i) vis[d[i]] = 1;
build();
dfs3(d[1]);
printf("%lld\n", dp[d[1]]);
}
return 0;
}
bzoj3572 每次给出几个点做议事处,问离这些点最近的其他点的数量,如到两个议事处的距离相同,选顶点编号小的议事处。
根据询问点建虚树,因为虚树不止有询问的点,还有他们的lca,所以先对建出来的虚树预处理出来虚树上每个点离他最近的议事处的距离和点的编号(自己就是议事处肯定就是自己,主要是对增加的lca进行处理)。
因为最近的点可能来自下面的点也可能是上面的点,所以跑两次dfs从两个方向更新一下即可。
对于虚树的一条边来说,两个点都有其对应的议事处,它们之间的边代表原树上的一些点(或者说子树)。对于每条边我们都计算一下两个点对应的议事处的分界点(注意不是这个点本身,以为它可能不是议事处而是新增的lca)即可。方法是用倍增从深度最大的那个点往上跳,计算跳到的那个点当分界点时到两个议事处的距离,注意还要考虑距离相等编号选最小的议事处。
还有一个细节需要注意,对于点u和点v(u是v的祖先),我们计算分界点d分开的点的数量不能直接加上sz[u]-sz[d],因为u有好几个子树,这样加肯定会重复,可以算出u的儿子son,满足son是v的祖先,这样每次减去sz[son],加上sz[son]-sz[d],最后再加上sz[u]就行了。
const int maxn = 6e5+10;
struct E {
int to, nxt;
} e[maxn];
int h[maxn], tot;
void add(int u, int v) {
e[++tot] = {v, h[u]};
h[u] = tot;
}
int ldfn[maxn], rdfn[maxn], tim;
int dep[maxn], f[maxn][20], sz[maxn];
void dfs(int u, int p) {
//cout << "!" << u << endl;
ldfn[u] = ++tim; sz[u] = 1;
for (int i = h[u]; i; i=e[i].nxt) {
int v = e[i].to;
if (v==p) continue;
dep[v] = dep[u]+1;
f[v][0] = u;
for (int j = 1; j<20; ++j) f[v][j] = f[f[v][j-1]][j-1];
dfs(v, u);
sz[u] += sz[v];
}
rdfn[u] = tim;
}
int lca(int u, int v) {
if (dep[u]<dep[v]) swap(u, v);
for (int i = 19; i>=0; --i)
if (dep[f[u][i]]>=dep[v]) u = f[u][i];
if (u==v) return u;
for (int i = 19; i>=0; --i)
if (f[u][i]!=f[v][i]) u = f[u][i], v = f[v][i];
return f[u][0];
}
int n, m, k, d[maxn], sk[maxn], vis[maxn];
void build() {
tot = 0; //!!!!
sort(d+1, d+k+1, [](int a, int b) {return ldfn[a]<ldfn[b];});
//for (int i = 1; i<=k; ++i) cout << d[i] << (i==k ? '\n':' ');
int keynum = k;
for (int i = 1; i<keynum; ++i) d[++k] = lca(d[i], d[i+1]);
sort(d+1, d+k+1, [](int a, int b) {return ldfn[a]<ldfn[b];});
k = unique(d+1, d+k+1)-d-1;
int tp = 1; sk[tp] = d[1];
for (int i = 2; i<=k; ++i) {
while(tp && rdfn[sk[tp]]<ldfn[d[i]]) --tp;
if (tp) add(sk[tp], d[i]);
sk[++tp] = d[i];
}
}
int dp[maxn], g[maxn];
void dfs1(int u, int p) {
dp[u] = INF;
for (int i = h[u]; i; i=e[i].nxt) {
int v = e[i].to;
if (v==p) continue;
dfs1(v, u);
int dis = dep[v]-dep[u]; //cout << dis << endl; //注意相同距离取编号小的
if (dp[v]+dis<dp[u] || (dp[v]+dis==dp[u]&&g[v]<g[u])) dp[u] = dp[v]+dis, g[u] = g[v];
//cout << "!" << u << ' ' << v << ' ' << g[u] << ' ' << dp[u] << endl;
}
if (vis[u]) dp[u] = 0, g[u] = u;
}
void dfs2(int u, int p) {
for (int i = h[u]; i; i=e[i].nxt) {
int v = e[i].to;
if (v==p) continue;
int dis = dep[v]-dep[u]; //cout << dis << endl; //注意相同距离取编号小的
if (dp[u]+dis<dp[v] || (dp[u]+dis==dp[v]&&g[u]<g[v])) dp[v] = dp[u]+dis, g[v] = g[u];
dfs2(v, u);
}
}
int ans[maxn], tmp[maxn];
void calc(int u, int v) {
int son = v;
for (int i = 19; i>=0; --i)
if (dep[f[son][i]]>dep[u]) son = f[son][i];
ans[g[u]] -= sz[son]; //先减去儿子的贡献
//cout << ans[g[u]] << endl;
int d = v;
for (int i = 19; i>=0; --i) {
int t = f[d][i];
if (dep[t]<dep[u]) continue; //倍增往上找分界点
int l = dp[v]+dep[v]-dep[t], r = dp[u]+dep[t]-dep[u];
if (l<r || (l==r && g[v]<g[u])) d = t; //相同距离取最小
}
//cout << u << ' ' << g[u] << "|||" << v << ' ' << g[v] << "!!" << d << endl;
ans[g[u]] += sz[son]-sz[d]; ans[g[v]] += sz[d]-sz[v];
//cout << ans[g[u]] << ' ' << ans[g[v]] << endl;
}
void dfs3(int u, int p) {
for (int i = h[u]; i; i=e[i].nxt) {
int v = e[i].to;
if (v==p) continue;
calc(u, v);
dfs3(v, u);
}
ans[g[u]] += sz[u];
}
void init() {
tot = 0;
for (int i = 1; i<=k; ++i) h[d[i]] = ans[d[i]] = g[d[i]] = vis[d[i]] = 0, dp[d[i]]= INF;
}
int main() {
cin >> n;
for (int i = 1, a, b; i<n; ++i) {
scanf("%d%d", &a, &b);
add(a, b);
add(b, a);
}
dep[1] = 1; dfs(1, 0);
//for (int i = 1; i<=n; ++i) cout << ldfn[i] << ' ' << rdfn[i] << endl;
clr(h, 0); tot = 0; //清空原树
cin >> m;
while(m--) {
scanf("%d", &k); int tk = k;
for (int i = 1; i<=k; ++i) scanf("%d", &d[i]), tmp[i] = d[i];
for (int i = 1; i<=k; ++i) vis[d[i]] = 1;
if (!vis[1]) d[++k] = 1;
build();
//for (int i = 1; i<=k; ++i) printf(i==k ? "%d\n":"%d ", d[i]);
dfs1(1, 0);
//for (int i = 1; i<=k; ++i) cout << d[i] << ' ' << g[d[i]] << endl;
dfs2(1, 0); dfs3(1, 0);
//for (int i = 1; i<=k; ++i) cout << d[i] << ' ' << g[d[i]] << endl;
for (int i = 1; i<=tk; ++i) printf(i==tk ? "%d\n":"%d ", ans[tmp[i]]);
init();
}
return 0;
}
计算几何
分数表示斜率
gym 102220C 给你n条直线,计算交叉直线数量,重合也算,模板题
typedef pair<int, int> P;
struct INFO {
ll k1, k2, b;
bool operator < (INFO a) const {
if (b==a.b) return k1==a.k1 ? k2<a.k2:k1<a.k1;
return b<a.b;
}
};
map<INFO, int> mp;
map<P, int> mp2;
int main() {
int __; cin >> __;
while(__--) {
int n; scanf("%d", &n);
for (int i = 1; i<=n; ++i) {
int a, b, c, d; scanf("%d%d%d%d", &a, &b, &c, &d);
ll t1 = a-c;
ll t2 = b-d;
if (t1==0) ++mp[{0, 0, a}], ++mp2[{0, 0}]; //斜率为0
else if (t2==0) ++mp[{INF, 0, b}], ++mp2[{INF, 0}]; //斜率不存在
else {
ll g = __gcd(t1, t2);
t1 /= g;
t2 /= g;
ll k = b - 1LL * t2 * a / t2;
++mp[{t1, t2, k}]; //存直线
++mp2[{t1,t2}]; //计算斜率相同的直线数量
}
}
ll ans = 0;
for (auto v : mp) {
ans += 1LL*(n-mp2[{v.first.k1, v.first.k2}])*v.second; //斜率不同的直线必定交叉
}
ans /= 2;
for (auto v : mp) {
ans += 1LL*v.second*(v.second-1)/2; //重合的直线算成c(m, 2)
}
cout << ans << endl;
mp.clear(); mp2.clear();
}
return 0;
}
分数类
HDU 6206 给4个点,保证任意3点不共线,问第4个点是否被包括在前3个点的圆上。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
struct frac
{
__int128 p,q;
frac(){}
frac(__int128 _p,__int128 _q)
{
if(_q<0) _p=-_p,_q=-_q;
p=_p,q=_q;
}
frac operator +(const frac&rhs)
{
__int128 a,b;
b=q*rhs.q;
a=p*rhs.q+q*rhs.p;
if(b==0) return frac(0,1);
__int128 g=__gcd(a,b);
a/=g;
b/=g;
return frac(a,b);
}
frac operator -(const frac&rhs)
{
__int128 a,b;
b=q*rhs.q;
a=p*rhs.q-q*rhs.p;
if(b==0) return frac(0,1);
__int128 g=__gcd(a,b);
a/=g;
b/=g;
return frac(a,b);
}
frac operator *(const frac&rhs)
{
__int128 a,b;
b=q*rhs.q;
a=p*rhs.p;
if(b==0) return frac(0,1);
__int128 g=__gcd(a,b);
a/=g;
b/=g;
return frac(a,b);
}
frac operator /(const frac&rhs)
{
__int128 a,b;
b=q*rhs.p;
a=p*rhs.q;
if(b==0) return frac(0,1);
__int128 g=__gcd(a,b);
a/=g;
b/=g;
return frac(a,b);
}
bool operator <(const frac&rhs)const
{
return p*rhs.q<rhs.p*q;
}
bool operator >(const frac&rhs)const
{
return p*rhs.q>rhs.p*q;
}
bool operator ==(const frac&rhs)const
{
return !(p*rhs.q<rhs.p*q)&&!(p*rhs.q>rhs.p*q);
}
};
struct Point
{
frac x,y;
void read()
{
LL t1,t2;
cin>>t1>>t2;
x=frac((__int128)t1,1),y=frac((__int128)t2,1);
}
Point(){}
Point(frac _x,frac _y)
{
x=_x,y=_y;
}
Point operator -(const Point& rhs)
{
return Point(x-rhs.x,y-rhs.y);
}
};
typedef Point Vector;
frac Dot(Vector A,Vector B)
{
return A.x*B.x+A.y*B.y;
}
Point waixin(Point a,Point b,Point c) {
frac a1 = b.x - a.x, b1 = b.y - a.y, c1 = (a1*a1 + b1*b1)/frac(2,1);
frac a2 = c.x - a.x, b2 = c.y - a.y, c2 = (a2*a2 + b2*b2)/frac(2,1);
frac d = a1*b2 - a2*b1;
return Point(a.x + (c1*b2 - c2*b1)/d, a.y + (a1*c2 -a2*c1)/d);
}
Point p1,p2,p3,c,p;
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
p1.read();
p2.read();
p3.read();
c=waixin(p1,p2,p3);
p.read();
if(Dot(p-c,p-c)>Dot(p1-c,p1-c))
puts("Accepted");
else
puts("Rejected");
}
}
三分
ll res = 2e18, res1 = 2e18, l = 1, r = 1e9;
while (l<=r) {
ll mi = (r-l+1)/3, ml = l+mi, mr = r-mi;
ll al = check(a, ml), ar= check(a, mr);
if(al>ar) {
l = ml+1;
res = min(res, ar);
}
else {
r = mr-1;
res = min(res, al);
}
}
杂项
平方和公式
\(n*(n+1)*(2*n+1)/2\)
两个最简分数之间的最简分数
设\(\frac{a}{b} < \frac{c}{d}\),那么\(\frac{a}{b} < \frac{a+c}{b+d} < \frac{c}{d}\)
快速构造勾股数
容易证明,下面的数字是勾股数:
这个公式并不能求出所有的勾股数,但是我们可以给三个数乘上一个系数,来构造其他的勾股数,下面以构造\(a\)的取值为[3, 40000]为例的代码。
for (int i = 1; 2*i+1<=40000; ++i) {
ll a = 2*i+1;
ll b = 2LL*i*(i+1);
ll c = 2LL*i*(i+1)+1;
for (int j = 1; j*a<=40000; ++j) {
if (trp[a*j].b!=0) continue;
trp[a*j] = {b*j, c*j};
}
}
trp[4] = {5, 3};
for (int j = 1; j*4<=40000; ++j) {
ll a = 4;
ll b = 3;
ll c = 5;
if (trp[a*j].b!=0) continue;
trp[a*j] = {b*j, c*j};
}
短除法进制转换
int getnum(char ch) { //字符转数字
if(ch <= '9') return ch-'0';
else if(ch <= 'Z') return 10+ch-'A';
else return 36+ch-'a';
}
char getch(int num) { //数字转字符
if(num <= 9) return num+'0';
else if(num <= 35) return num-10+'A';
else return num-36+'a';
}
int n,m;
char str1[maxn],str2[maxn];
int t[maxn],ans[maxn];
void solve() {
int len = strlen(str1);
for(int i = 0; i < len; i++) //先把字符串变成数组,高位->低位
t[i] = getnum(str1[i]);
int j = 0,k = 0;
while(j < len) {
for(int i = j; i < len-1; i++) { //除以m,把余数加到下一位
t[i+1] += t[i] % m * n;
t[i] /= m;
}
ans[k++] = t[len-1]%m; //个位数余m
t[len-1] /= m;
while(j < len && !t[j]) j++; //最高位是0,j++
}
for(int i = 0; i < k; i++) //逆序变成字符串
str2[i] = getch(ans[k-i-1]);
}
int main() {
cin >> n >> m;
cin>> str1;
solve();
cout<< str2 << endl << endl;
}
约瑟夫问题
考虑每数到3出局一个
开始:1,2,3,4,5,6...
3出局:4,5,6...1,2
可以发现第二轮所有数加上3再对其个数取模即为第一轮的情况,递推式为(now+k-1)%num+1,num为当前数字个数,k为数到k的人出局,now为答案。
对于上面的递推式还可以加速处理,当now+k-1小于num时,我们可以在其小于num时尽量多加几个k-1,代码如下:
ll now = 0, i = n-m+1; //一共n个人,进行了m轮
if (k==1) now = m;
else {
while(i<=n) {
ll t = min((i-now)/k, n-i); //最多再进行n-i轮
if (t) now = now+t*k, i += t;
else now = (now+k-1)%i+1, ++i;
}
}
树的最小表示
//给两个字符串描述两个树,0表示向下扩展,1表示回溯,问两个树是否同构
const int maxn = 1e5+10;
int u,p[maxn];
string dfs(string s) {
++u;
vector<string> tmp;
while(s[u]=='0') tmp.push_back(dfs(s));
++u;
sort(tmp.begin(),tmp.end());
string res = "0";
for (auto s : tmp) res += s;
res += '1';
return res;
}
int main(){
int t; cin >> t;
while(t--) {
string s1,s2;
cin >> s1 >> s2;
s1 = '0'+s1+'1';
s2 = '0'+s2+'1';
u = 0; string rs1 = dfs(s1);
u = 0; string rs2 = dfs(s2);
if (rs1==rs2) puts("same");
else puts("different");
}
return 0;
}
大数
#include <algorithm>
#include <cstdio>
#include <string>
#include <vector>
struct BigIntTiny {
int sign;
std::vector<int> v;
BigIntTiny() : sign(1) {}
BigIntTiny(const std::string &s) { *this = s; }
BigIntTiny(int v) {
char buf[21];
sprintf(buf, "%d", v);
*this = buf;
}
void zip(int unzip) {
if (unzip == 0) {
for (int i = 0; i < (int)v.size(); i++)
v[i] = get_pos(i * 4) + get_pos(i * 4 + 1) * 10 + get_pos(i * 4 + 2) * 100 + get_pos(i * 4 + 3) * 1000;
} else
for (int i = (v.resize(v.size() * 4), (int)v.size() - 1), a; i >= 0; i--)
a = (i % 4 >= 2) ? v[i / 4] / 100 : v[i / 4] % 100, v[i] = (i & 1) ? a / 10 : a % 10;
setsign(1, 1);
}
int get_pos(unsigned pos) const { return pos >= v.size() ? 0 : v[pos]; }
BigIntTiny &setsign(int newsign, int rev) {
for (int i = (int)v.size() - 1; i > 0 && v[i] == 0; i--)
v.erase(v.begin() + i);
sign = (v.size() == 0 || (v.size() == 1 && v[0] == 0)) ? 1 : (rev ? newsign * sign : newsign);
return *this;
}
std::string to_str() const {
BigIntTiny b = *this;
std::string s;
for (int i = (b.zip(1), 0); i < (int)b.v.size(); ++i)
s += char(*(b.v.rbegin() + i) + '0');
return (sign < 0 ? "-" : "") + (s.empty() ? std::string("0") : s);
}
bool absless(const BigIntTiny &b) const {
if (v.size() != b.v.size()) return v.size() < b.v.size();
for (int i = (int)v.size() - 1; i >= 0; i--)
if (v[i] != b.v[i]) return v[i] < b.v[i];
return false;
}
BigIntTiny operator-() const {
BigIntTiny c = *this;
c.sign = (v.size() > 1 || v[0]) ? -c.sign : 1;
return c;
}
BigIntTiny &operator=(const std::string &s) {
if (s[0] == '-')
*this = s.substr(1);
else {
for (int i = (v.clear(), 0); i < (int)s.size(); ++i)
v.push_back(*(s.rbegin() + i) - '0');
zip(0);
}
return setsign(s[0] == '-' ? -1 : 1, sign = 1);
}
bool operator<(const BigIntTiny &b) const {
return sign != b.sign ? sign < b.sign : (sign == 1 ? absless(b) : !absless(b));
}
bool operator==(const BigIntTiny &b) const { return v == b.v && sign == b.sign; }
BigIntTiny &operator+=(const BigIntTiny &b) {
if (sign != b.sign) return *this = (*this) - -b;
v.resize(std::max(v.size(), b.v.size()) + 1);
for (int i = 0, carry = 0; i < (int)b.v.size() || carry; i++) {
carry += v[i] + b.get_pos(i);
v[i] = carry % 10000, carry /= 10000;
}
return setsign(sign, 0);
}
BigIntTiny operator+(const BigIntTiny &b) const {
BigIntTiny c = *this;
return c += b;
}
void add_mul(const BigIntTiny &b, int mul) {
v.resize(std::max(v.size(), b.v.size()) + 2);
for (int i = 0, carry = 0; i < (int)b.v.size() || carry; i++) {
carry += v[i] + b.get_pos(i) * mul;
v[i] = carry % 10000, carry /= 10000;
}
}
BigIntTiny operator-(const BigIntTiny &b) const {
if (sign != b.sign) return (*this) + -b;
if (absless(b)) return -(b - *this);
BigIntTiny c;
for (int i = 0, borrow = 0; i < (int)v.size(); i++) {
borrow += v[i] - b.get_pos(i);
c.v.push_back(borrow);
c.v.back() -= 10000 * (borrow >>= 31);
}
return c.setsign(sign, 0);
}
BigIntTiny operator*(const BigIntTiny &b) const {
if (b < *this) return b * *this;
BigIntTiny c, d = b;
for (int i = 0; i < (int)v.size(); i++, d.v.insert(d.v.begin(), 0))
c.add_mul(d, v[i]);
return c.setsign(sign * b.sign, 0);
}
BigIntTiny operator/(const BigIntTiny &b) const {
BigIntTiny c, d;
d.v.resize(v.size());
double db = 1.0 / (b.v.back() + (b.get_pos((unsigned)b.v.size() - 2) / 1e4) +
(b.get_pos((unsigned)b.v.size() - 3) + 1) / 1e8);
for (int i = (int)v.size() - 1; i >= 0; i--) {
c.v.insert(c.v.begin(), v[i]);
int m = (int)((c.get_pos((int)b.v.size()) * 10000 + c.get_pos((int)b.v.size() - 1)) * db);
c = c - b * m, d.v[i] += m;
while (!(c < b))
c = c - b, d.v[i] += 1;
}
return d.setsign(sign * b.sign, 0);
}
BigIntTiny operator%(const BigIntTiny &b) const { return *this - *this / b * b; }
bool operator>(const BigIntTiny &b) const { return b < *this; }
bool operator<=(const BigIntTiny &b) const { return !(b < *this); }
bool operator>=(const BigIntTiny &b) const { return !(*this < b); }
bool operator!=(const BigIntTiny &b) const { return !(*this == b); }
};


