Codeforces 1294E Obtain a Permutation(思维)

题目链接

题目大意

  给一个矩阵，修改方式有两种，求把矩阵修改成下面形式的最小修改次数。
  1.任选一个数字并把它变成任意一个数字。
  2.任选一列让所有数字所在的行数+1，第一行变成最后一行。

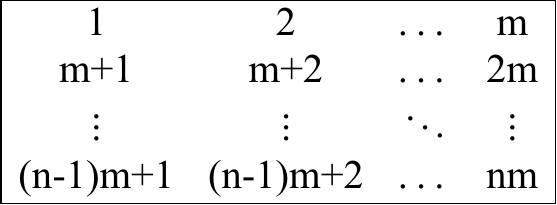
分析

  1.如果某个数应该存在在当前列中，那么可以通过操作2来把它改到对应位置或者通过操作1来修改它的值。
  2.如果某个数不应该存在在当前列里，那么只能通过操作1来修改这个数。
  3.如果一列数中的某些数字的相对位置是正确的，那么只要其中一个移动到正确的位置剩下的也会移动到正确的位置。

具体实现

  对于每一列，我们可以默认一开始所有的数都要修改，然后统计每个数字移动到正确的位置需要移动的次数，如果可以通过较少的移动来让更多的数字移动的正确的位置的话，答案就是更优的。可能是我写的代码太丑了吧，需要注意一些细节，这点看代码里的注释。

代码

const int maxn = 2e5+10;
int n, m, cnt[maxn];
vector<int> g[maxn];
int main(void) {
    cin>>n>>m;
    for (int i = 0; i<n; ++i)
        for (int j = 0, num; j<m; ++j) {
            cin >> num;
            g[i].push_back(num);
        }
    int ans = 0;
    for (int i = 0; i<m; ++i) {
        int tmp = n;
        for (int j = 0; j<n; ++j) {
            int t = g[j][i]-i-1; //因为我的i是从0开始的，所以这里fix一下
            if (t/m>=n) continue; //从图中可以看到最大的数减去第一个数后只能等于n*(m-1)
            if (!(t%m)) { //减去第一个数后必须是m的倍数
                int t2 = (j-t/m+n)%n; //移动的次数，因为只能每行的数只能向上移动，所以一个较小的行
                //移动到较大的行的时候会出现负数，所以取一下模
                ++cnt[t2]; 
                tmp = min(tmp, n-cnt[t2]+t2);
            }
        }
        ans += tmp;
        memset(cnt, 0, sizeof(cnt[0])*(n+5));
    }
    cout << ans << endl;
    return 0;
}