AcWing - 99 -激光炸弹(二维前缀和)

题目链接
  二维前缀和模板题，首先我们得先了解一下二维前缀和怎么求。
  1.首先我们先对第一行与第一列做一下处理，显然，对于第一行\(g[0][i] = g[0][i] + g[0][i-1]\)，对于第一列\(g[i][0] = g[i][0] + g[i-1][0]\)。
  2.然后我们考虑位于其他位置的前缀和怎么处理，这里我们可以用容斥原理的思想来做：

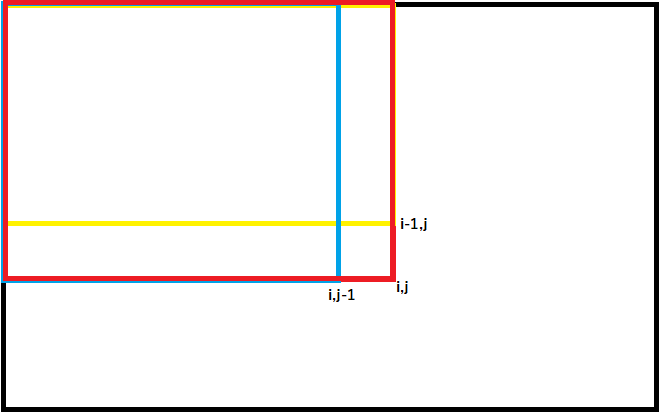
  如图，我们想求红色部分的面积，而我们只知道红色矩形右下角的面积和黄蓝矩形的面积，那么可以通过红色矩形一角的面积加上蓝色矩形和黄色矩形的面积再减去蓝黄矩阵相互重叠的部分。
即\(g[i][j] = g[i][j] + g[i-1][j] + g[i][j-1] - g[i-1][j-1]\)。
  知道了这些我们就可以先对这个矩形求一个二维的前缀和，然后在遍历一下所有边长为r的矩形包括的点的个数的最大值就可以了。求法和上面类似：
\(ans = g[i][j] - g[i-r-1][j] - g[i][j-r-1] + g[i-r-1][j-r-1]\)
  这里需要注意一个问题，炸弹每次爆炸的时候，位于炸弹爆炸范围边上的点是不能计算的。那么我们怎么做呢？我们把每个目标的横、纵左边+1，这样原本位于右边和下边的点就会移动到矩形边缘的外侧，那么在矩形左边和上边的点呢？我们对上面的公式修改一下，把矩形的左边缘和上边缘的值也减掉就可以了：
\(ans = g[i][j] - g[i-r][j] - g[i][j-r] + g[i-r][j-r]\)。

//https://www.cnblogs.com/shuitiangong/
#include<set>
#include<map>
#include<list>
#include<stack>
#include<queue>
#include<cmath>
#include<cstdio>
#include<cctype>
#include<string>
#include<vector>
#include<climits>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define endl '\n'
#define rtl rt<<1
#define rtr rt<<1|1
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define maxx(a, b) (a > b ? a : b)
#define minn(a, b) (a < b ? a : b)
#define zero(a) memset(a, 0, sizeof(a))
#define INF(a) memset(a, 0x3f, sizeof(a))
#define IOS ios::sync_with_stdio(false)
#define _test printf("==================================================\n")
using namespace std;
typedef long long ll;
typedef pair<int, int> P;
typedef pair<ll, ll> P2;
const double pi = acos(-1.0);
const double eps = 1e-7;
const ll MOD =  9901;
const int INF = 0x3f3f3f3f;
const int _NAN = -0x3f3f3f3f;
const double EULC = 0.5772156649015328;
const int NIL = -1;
template<typename T> void read(T &x){
    x = 0;char ch = getchar();ll f = 1;
    while(!isdigit(ch)){if(ch == '-')f*=-1;ch=getchar();}
    while(isdigit(ch)){x = x*10+ch-48;ch=getchar();}x*=f;
}
const int maxn = 5e3+10;
int g[maxn][maxn];
int main(void) {
    int n, r;
    scanf("%d%d", &n, &r);
    if (r > maxn) r = 5000;
    for (int i = 0, a, b, w; i<n; ++i) {
        scanf("%d%d%d", &a, &b, &w);
        g[a+1][b+1] += w;
    }
    for (int i = 1; i<maxn; ++i) {
        g[0][i] += g[0][i-1]; //处理第一行
        g[i][0] += g[i-1][0]; //处理第一列
    }
    for (int i = 1; i<maxn; ++i)
        for (int j = 1; j<maxn; ++j)
            g[i][j] += g[i-1][j] + g[i][j-1] - g[i-1][j-1]; //计算二维前缀和
    int ans = 0;
    for (int i = r; i<maxn; ++i)
        for (int j = r; j<maxn; ++j)
            ans = max(ans, g[i][j]-g[i-r][j]-g[i][j-r]+g[i-r][j-r]);
    printf("%d\n", ans);
    return 0;
}