排序算法 之 （直接插入排序）
10.6、堆排序
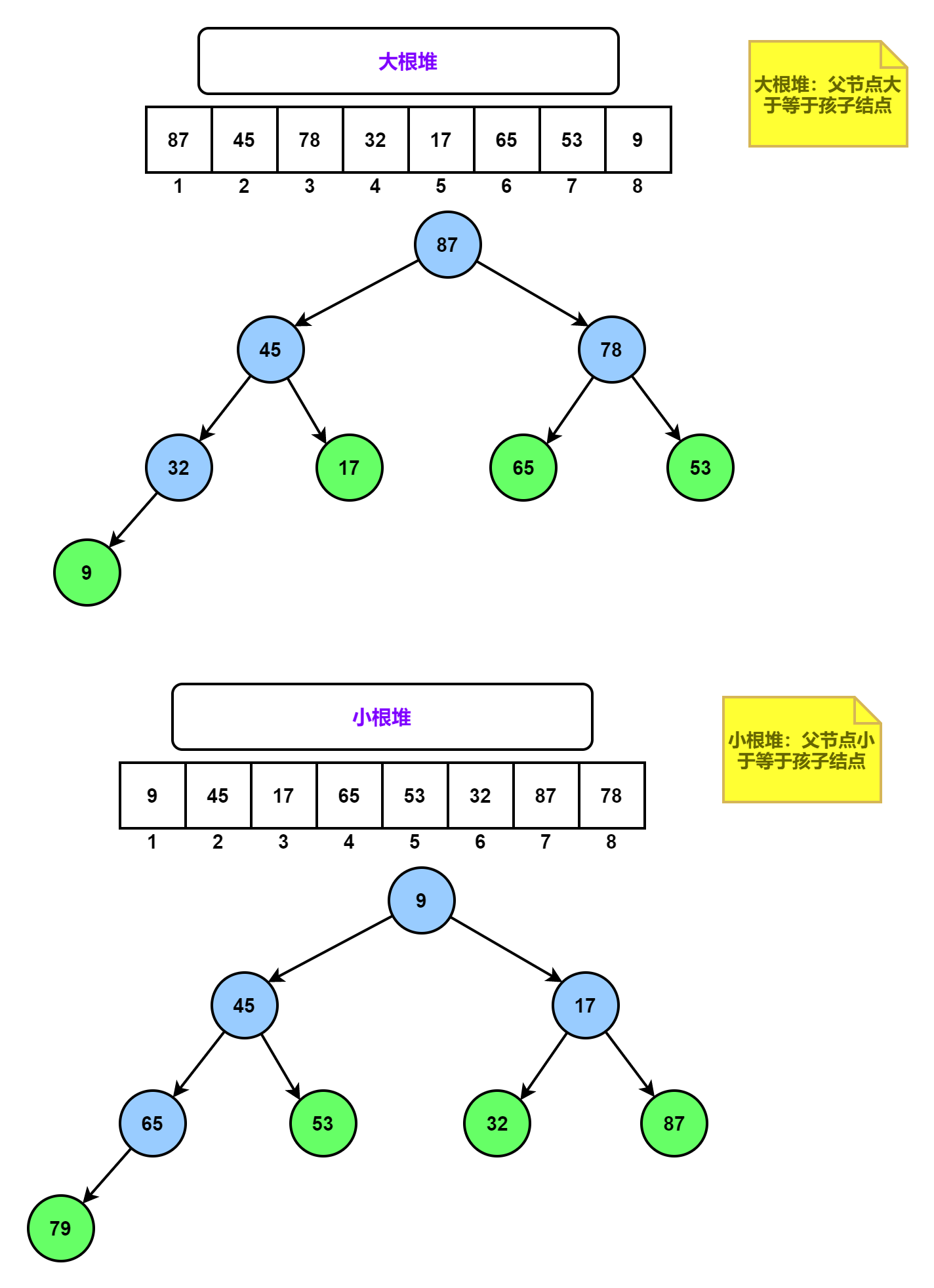
对于n个关键字序列L[1...n]，满足下面某一条性质，则称为堆（Heap）
- 若满足：\(L(2i) \le L(i)\)且\(L(2i+1) \le L(i)\)，\(1 \le i \le n\) ，大根堆(大顶堆)
- 若满足：\(L(i) \le L(2i)\)且\(L(i) \le L(2i+1)\)，\(1 \le i \le n\) ，小根堆(小顶堆)
这里需要了解二叉树的顺序存储，对于n个结点的关键字来说
\(\left \lfloor \frac{n}{2} \right \rfloor < i\)这里\(i\)就是叶子结点，
$ i \le \left \lfloor \frac{n}{2} \right \rfloor$ 这里\(i\)就是分支结点（非叶子结点）；
分支结点的\(i\)，左孩子：\(2i\)，右孩子：\(2i + 1\)
大根堆： 左孩子、右孩子 \(\le\) 父节点
小根堆：父节点 \(\le\) 左孩子、右孩子
堆排序是不稳定的
图解大根堆、小根堆
那么应该如何建立大根堆（小根堆）了；
思路：看非叶子结点是否满足大根堆（小根堆）要求，如果不满足进行调整
图解过程
小根堆的建立也差不多；
大根堆的排序过程图解
首先，就是交换大根堆堆顶元素和最后一个为排序的元素，交换后最后一个就是该元素的排序的位置，现在需要堆顶元素进行大根堆化；然后重复操作直到全部排序完成
大（小）根堆排序的代码实现
#include <stdio.h>
#include <stdlib.h>
#define boolean int
#define false 0;
#define true 1;
//大根堆排序，将以k为根的子树调整为大根堆
void HeadAdjust(int nums[],int k,int len){
int temp = nums[k];//暂存子树的根结点
for(int i=2*(k+1)-1;i <= len;i = i*2 + 1){//沿着k较大的结点，向下筛选
if(i < len && nums[i] < nums[i+1]){//看左孩子和右孩子那个大，取那个
i++;
}
if(temp >= nums[i]) break;//根结点大，就不需要交换，返回
else{
nums[k] = nums[i]; //否则交换
k = i; //修改k值，继续向下筛选
}
}
nums[k] = temp; //被筛选的结点放入最终位置
}
//建立大根堆
void BuildMaxHeap(int nums[] ,int length){
for(int i = length/2-1;i>=0;i--){ //从后往前非叶子结点进行大根堆初始化
HeadAdjust(nums,i,length-1);
}
}
//堆排序（大根堆）
void MaxHeapSort(int nums[],int length){
BuildMaxHeap(nums,length);//建立大根堆
for(int i = length-1;i > 0;i--){
//交换堆顶和堆堆尾
int temp = nums[i];
nums[i] = nums[0];
nums[0] = temp;
HeadAdjust(nums,0,i-1);//把新的堆变成大根堆
}
}
//小根堆排序，将以k为根的子树调整为小根堆
void HeadAdjust1(int nums[],int k,int len){
int temp = nums[k];//暂存子树的根结点
for(int i=2*(k+1)-1;i <= len;i = i*2 + 1){//沿着k较大的结点，向下筛选
if(i < len && nums[i] > nums[i+1]){//看左孩子和右孩子那个大，取那个
i++;
}
if(temp <= nums[i]) break;//根结点大，就不需要交换，返回
else{
nums[k] = nums[i]; //否则交换
k = i; //修改k值，继续向下筛选
}
}
nums[k] = temp; //被筛选的结点放入最终位置
}
//建立小根堆
void BuildMinHeap(int nums[] ,int length){
for(int i = length/2 - 1;i>=0;i--){ //从后往前非叶子结点进行大根堆初始化
HeadAdjust1(nums,i,length-1);
}
}
//堆排序（小根堆）
void MinHeapSort(int nums[],int length){
BuildMinHeap(nums,length);//建立大根堆
for(int i = length-1;i > 0;i--){
//交换堆顶和堆堆尾
int temp = nums[i];
nums[i] = nums[0];
nums[0] = temp;
HeadAdjust1(nums,0,i-1);//把新的堆变成大根堆
}
}
int main(){
int nums[] = {53,17,78,9,45,65,87,32};
int length = 8;
printf("堆（大根堆）排序前：");
for(int i = 0; i < length ;i++){
printf("%d ",nums[i]);
}
MaxHeapSort(nums,length);
printf("\n");
printf("堆（大根堆）排序后：");
for(int i = 0; i < length ;i++){
printf("%d ",nums[i]);
}
printf("\n");
int nums1[] = {49,38,65,97,76,13,27,47,89,13,48,76,88,88,99};
int length1 = 15;
printf("堆（小根堆）排序前：");
for(int i = 0; i < length1 ;i++){
printf("%d ",nums1[i]);
}
MinHeapSort(nums1,length1);
printf("\n");
printf("堆（小根堆）排序后：");
for(int i = 0; i < length1 ;i++){
printf("%d ",nums1[i]);
}
return 0;
}
//结果：
堆（大根堆）排序前：53 17 78 9 45 65 87 32
堆（大根堆）排序后：9 17 32 45 53 65 78 87
堆（小根堆）排序前：49 38 65 97 76 13 27 47 89 13 48 76 88 88 99
堆（小根堆）排序后：99 97 89 88 88 76 76 65 49 48 47 38 27 13 13
堆中插入一个新的元素
对于小根堆而言，新元素放到表尾，与父节点$\left \lfloor \frac{i} {2} \right \rfloor $ 这个结点进行对比，如果比父结点小就交换，交换后，继续与交换后的父结点对比，直到比它小或者到根了就结束
堆中插入一个元素图解
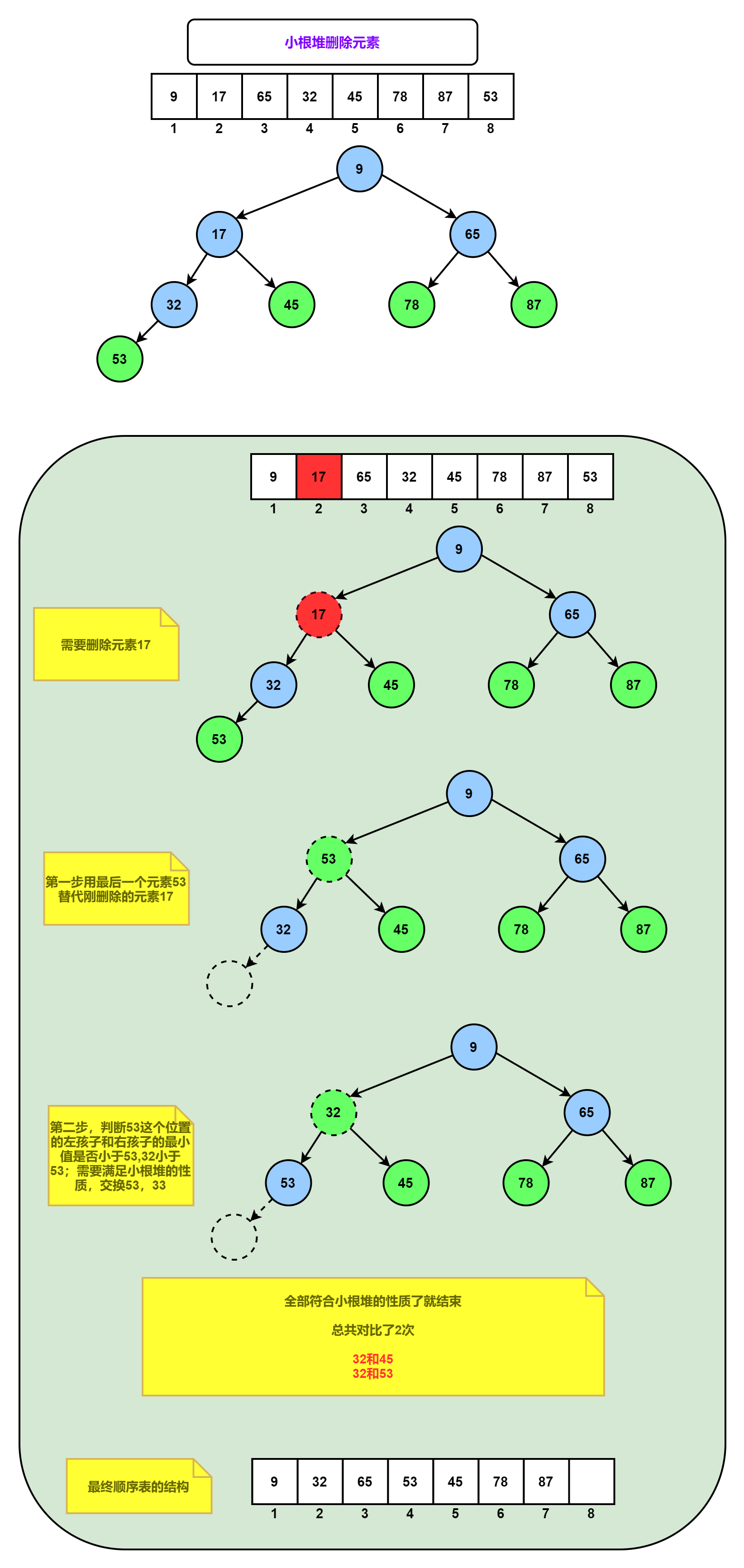
堆中删除一个元素
删除的元素如果不是最后一个，就使用最后一个代替它，然后对它进行小根堆化
堆中删除元素的图解
