yolov5数据增强引发的思考——透视变换矩阵的创建
yolov5的数据增强中，透视、仿射变换统一使用了random_perspective一个函数进行处理，包含了旋转、缩放、平移、剪切变换(shear,实际是按坐标轴方向变换，具体可看下文)、透视。其中下面这段代码的这个参数有点疑惑，因此寻找了不少透视变换的资料，这里记录我自己的思考。
仿射变换
仿射变换主要包括旋转、缩放、平移、shear等，仿射变换矩阵可以由旋转矩阵、平移矩阵等组合得到，仿射变换矩阵可以用如下矩阵表示。参考来源
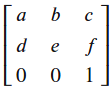
旋转、平移等基础变换矩阵如下图所示，random_perspective函数内部也是根据相应旋转角度等参数构建相应的矩阵并组合起来。
透视变换
回到开始说的，yolov5源码说的透视参数对应矩阵M[2,0],M[2,1]，random_perspective函数也只是建议参数范围0~0.001，前面的旋转、平移、缩放、shear参数都有具体含义并得到相应的矩阵，透视变换相关的参数却只是给出了数值范围，因此困惑于这个参数具体代表什么含义？
查找很多资料，基本都是opencv怎么使用透视变换、或者怎么实现求解透视变换矩阵的问题（可参考链接）。我想知道的是，透视变换矩阵是怎样由旋转、平移等基本操作矩阵组合而来的，即矩阵M[2,0],M[2,1]参数是怎样的操作得到的。
于是想到透视变换是把图像投影到新的视平面，如上图所示，新平面如果与原图像平面平行那就是简单的仿射变换，不平行那就是绕x/y轴发生了旋转，即空间点的旋转变换。空间坐标系转换。
因此perspective参数应该是绕x，y轴旋转矩阵产生。
测试程序如下
def __mylearn():
colors = [(0, 0, 255), (255, 0, 0)]#红色绘制原始框，蓝色绘制变换后的框
lw = 1
#voc数据集的一张图片数据
img = cv2.imread('../examples/2008_000109.jpg')
src = img.copy()
h, w, c = img.shape
cx, cy = w / 2, h / 2
bboxs = np.loadtxt('../examples/2008_000109.txt')
cw, ch = 0.5 * bboxs[:, 3], 0.5 * bboxs[:, 4]
bboxs[:, 3] = bboxs[:, 1] + cw
bboxs[:, 4] = bboxs[:, 2] + ch
bboxs[:, 1] -= cw
bboxs[:, 2] -= ch
bboxs[:, [1, 3]] *= w
bboxs[:, [2, 4]] *= h
srcboxs = bboxs.round().astype(np.int)
#原始图像绘制bbox框
for box in srcboxs:
s = f'c{box[0]}'
cv2.rectangle(src, (box[1], box[2]), (box[3], box[4]), color=colors[0], thickness=lw)
cv2.putText(src, s, (box[1], box[2] - 2), cv2.FONT_HERSHEY_COMPLEX, 1.0, color=colors[0], thickness=lw)
rotate = 10
shear = 5
scale = 0.8
R, T1, T2, S, SH = np.eye(3), np.eye(3), np.eye(3), np.eye(3), np.eye(3)
cos = math.cos(-rotate / 180 * np.pi) # 图片坐标原点在左上角，该坐标系的逆时针与肉眼看照片方向相反
sin = math.sin(-rotate / 180 * np.pi)
R[0, 0] = R[1, 1] = cos # 旋转矩阵
R[0, 1] = -sin
R[1, 0] = sin
T1[0, 2] = -cx # 平移矩阵
T1[1, 2] = -cy
T2[0, 2] = cx # 平移矩阵
T2[1, 2] = cy
S[0, 0] = S[1, 1] = scale # 缩放矩阵
M = (T2 @ S @ R @ T1) # 注意左乘顺序，对应，平移-》旋转-》缩放-》平移
# M[:2]等价于cv2.getRotationMatrix2D(center=(cx, cy), angle=rotate, scale=scale)
img = cv2.warpAffine(src, M[:2], (w, h), borderValue=(114, 114, 114))
img=np.concatenate((src,img),axis=1)
cv2.imwrite('affine.jpg', img)
#再加上shear
SH[0, 1] = SH[1, 0] = math.tan(shear / 180 * np.pi) # 两个方向
M = (T2 @ S @ SH @ T1)
img = cv2.warpAffine(src, M[:2], (w, h), borderValue=(114, 114, 114))
#bboxs坐标转换
#srcboxs [n,5]
# M矩阵用于列向量相乘，这里需要用转置处理所有坐标
n=srcboxs.shape[0]
xy = np.ones((n * 4, 3))#齐次坐标
xy[:,:2]=srcboxs[:,[1,2,3,2,3,4,1,4]].reshape((n*4,2)) #顺时针xy,xy,xy,xy坐标
transbox=(xy@M.T)[:,:2].reshape((n,8)).round().astype(np.int)
for idx,box in enumerate(transbox):
s = f'c{srcboxs[idx,0]}'
cv2.line(img,(box[0], box[1]),(box[2], box[3]),color=colors[1],thickness=lw)
cv2.line(img, (box[2], box[3]), (box[4], box[5]), color=colors[1], thickness=lw)
cv2.line(img, (box[4], box[5]), (box[6], box[7]), color=colors[1], thickness=lw)
cv2.line(img, (box[6], box[7]), (box[0], box[1]), color=colors[1], thickness=lw)
cv2.putText(img, s, (box[0], box[1] - 2), cv2.FONT_HERSHEY_COMPLEX, 1.0, color=colors[1], thickness=lw)
img = np.concatenate((src, img), axis=1)
cv2.imwrite('shrear.jpg',img)
#透视变换
#src=cv2.imread('../examples/test.png')
P,RX,RY=np.eye(3),np.eye(3),np.eye(3)
k=0.9
def get_one_z(a,b,c):#z1,z2 get z (0~1)
z1 = (-b + math.sqrt(b ** 2 - 4 * a * c)) / (2 * a)
z2 = (-b - math.sqrt(b ** 2 - 4 * a * c)) / (2 * a)
if z1>0 and z1<1:
return z1
else:
return z2
# 绕x轴旋转
zx=get_one_z(1+w**2,-2,1-(k*w)**2)#一元二次方程求解
#ax=math.atan((1-zx)/(w*zx))
ax=math.asin((1-zx)/(k*w))
cosx, sinx= math.cos(ax), math.sin(ax)
RX[1, 1] = RX[2, 2] = cosx
RX[1, 2] = -sinx
RX[2, 1] = sinx
img=cv2.warpPerspective(src,RX,(w,h))
cv2.imwrite('perspective_rx.jpg', img)
# 图像中心双轴旋转
zy = get_one_z(1 + h ** 2, -2, 1 - (k * h) ** 2) # 一元二次方程求解
ay = math.atan((1 - zy) / (h * zy))
cosy, siny = math.cos(ay), math.sin(ay)
RY[0, 0] = RX[2, 2] = cosy
RY[0, 2] = siny
RY[2, 0] = -siny
P=RX@RY
print(P)
M=T2@P@T1
img = cv2.warpPerspective(src, M, (w, h))
xy=xy @ M.T
transbox = (xy[:, :2] / xy[:, 2:3]).reshape(n, 8).round().astype(np.int)
for idx, box in enumerate(transbox):
s = f'c{srcboxs[idx, 0]}'
cv2.line(img, (box[0], box[1]), (box[2], box[3]), color=colors[1], thickness=lw)
cv2.line(img, (box[2], box[3]), (box[4], box[5]), color=colors[1], thickness=lw)
cv2.line(img, (box[4], box[5]), (box[6], box[7]), color=colors[1], thickness=lw)
cv2.line(img, (box[6], box[7]), (box[0], box[1]), color=colors[1], thickness=lw)
cv2.putText(img, s, (box[0], box[1] - 2), cv2.FONT_HERSHEY_COMPLEX, 1.0, color=colors[1], thickness=lw)
img = np.concatenate((src, img), axis=1)
cv2.imwrite('perspective.jpg',img)
其中绕x,y轴的角度范围确定方式如下图，假设黑色垂直实线为视平面，绕x轴旋转alpha角度，空间点（0，y，z）透视后在视平面位置（0，y/z,1）处，即（0，0，1）~（0，y, z）段透视到视平面（0，0，1）~（0，y/z,1）段。我期望图像透视后整个y方向还占k比率范围。则有(1-z)**2+(hz)**2=(kh)**2,解得z后就可以求alpha大小
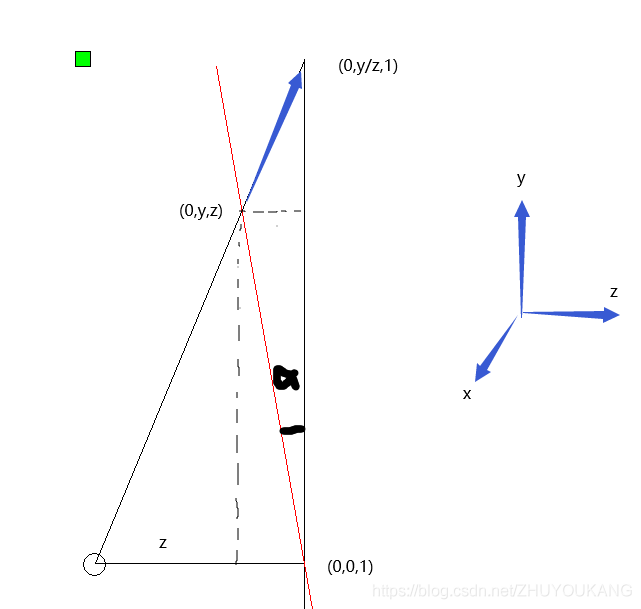
透视变换前后
这样就可以用基本操作设计透视矩阵。
k比较大时，如0.8，0.9，P矩阵如下。
与直接设置M[2,0],M[2,1]数量级接近了，设置k比直接设置random_perspective的perspective参数更容易调节透视变换效果。
不过实际图像增强中不会去使用旋转、透视等，因为若这样做原始的box变换后是倾斜的不规则的，无法获取用于训练的外接矩形框。
