PAT A1146 Topological Order (25分)
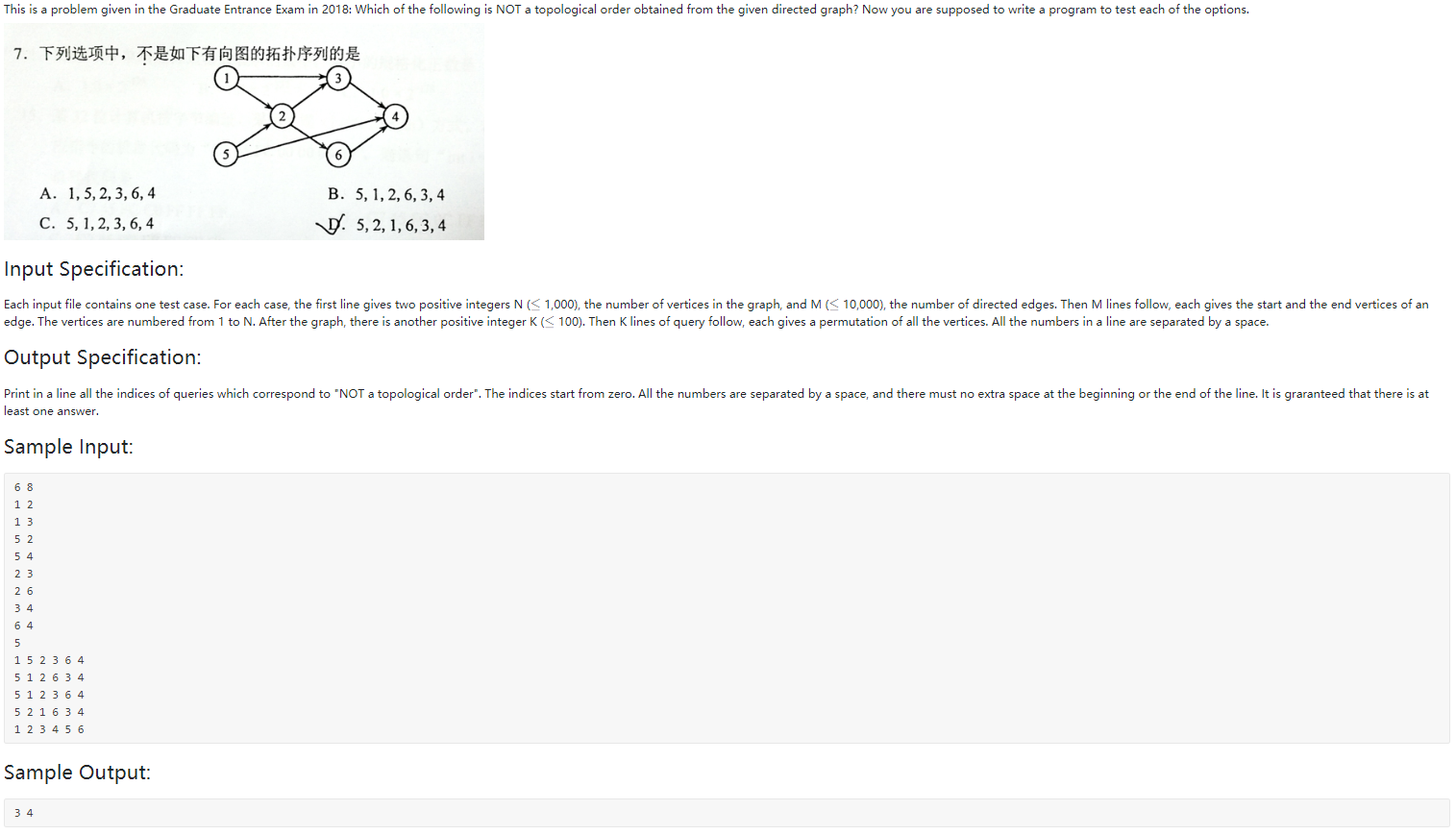
这是PAT图论中很少见拓扑排序问题,基本上不考,思路也偏向与验证排序正确与否,验证思路为:
在输入边的时候,记录所有顶点的单向邻接点,并且记录所有点的入度。查询时,每输入一个点,就判断其入度是否为0,不为0,则不是拓扑排序,然后将此点指向的所有点的入度减一,查询至结束,输出即可
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
const int N = 1010;
const int M = 10010;
const int K = 110;
vector<int>G[N];
int inDegree[N];
bool istopol[K];
int main(){
int n,m;
scanf("%d%d",&n,&m);
for(int i = 0 ; i < m ; i++){
int v,u;
scanf("%d%d",&v,&u);
G[v].push_back(u);//从v到u
inDegree[u]++;//u的入度+1
}
int k;
scanf("%d",&k);
fill(istopol,istopol+k,true);//先设置为全对
int tempinDegree[n+1];//0不用
int order[n];
for(int i = 0;i<k;i++){//k次验证
for(int j = 1;j<=n;j++){
tempinDegree[j] = inDegree[j];//复制入度
}
for(int j = 0;j < n;j++){
scanf("%d",order+j);
}
for(int j = 0;j< n;j++){
int v = order[j];
if(tempinDegree[v]!=0){
istopol[i] =false;
break;
}else{
for(int gt = 0;gt<G[v].size();gt++){
tempinDegree[G[v][gt]]--;//所有连接点入度-1
}
}
}
}
//print
bool flag = true;
for(int i = 0;i<k;i++){
if(istopol[i]==false){
if(flag==false) printf(" ");
printf("%d",i);
flag = false;
}
}
}


