PID算法的简单了解
什么是PID?
- PID是Proportional(比例)、Integral(积分)、Differential(微分)的缩写。
- PID控制算法是结合比例、积分和微分三种环节于一体的控制算法,它是连续系统中技术最为成熟、应用最为广泛的一种控制算法。
- PID Control,即PID控制器是以PID为原理制造的,在实际生产生活中,为了提高自动化能力,而最常见的控制器。
比如四轴飞行器,再比如平衡小车......还有汽车的定速巡航、3D打印机上的温度控制器....用“开关量”来控制一个物理量,就显得比较简单粗暴了。有时候,是无法保持稳定的。因为单片机、传感器不是无限快的,采集、控制需要时间。
这时,就需要一种『算法』:
它可以将需要控制的物理量带到目标附近
它可以“预见”这个量的变化趋势
它也可以消除因为散热、阻力等因素造成的静态误差
它就是PID算法
开环控制系统与闭环控制系统
在了解什么PID的各部分作用之前需要先了解什么是开环控制系统与闭环控制系统。
开环控制系统
定义:
- 开环控制系统是指无被控量反馈的控制系统,即需要控制的是被控对象的某一量(被控量),而测量的只是给定信号,被控量对于控制作用没有任何影响的系统。
- 可以不用直接测量扰动就组织起一个控制,只要监视由扰动对被控系统造成的偏差就行了。
- 简单来讲就是输出只受系统输入控制的没有反馈回路的系统,因此,开环控制系统又称为无反馈控制系统。
结构如图所示:
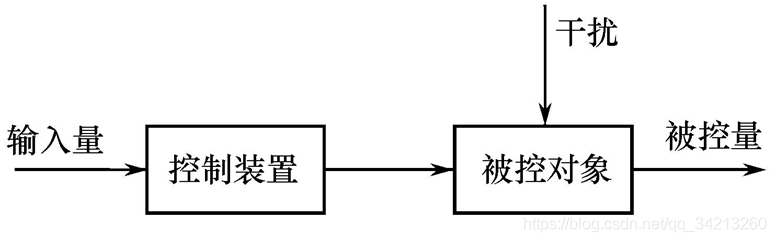
应用:开环控制系统主要是用于增强型的系统。
例如:指令输入计算机控制系统、驱动步进电机运动、电风扇(不能根据环境温度自动调节)、灯的开关、洗衣机、步进电机控制装置以及水位调节系统等。
闭环控制系统
定义:闭环控制系统是指有被控制量反馈的控制,其原理框如图所示。从系统中信号流向看,系统的输出信号沿反馈通道又回到系统的输入端,构成闭合通道,故称闭环控制系统,或反馈控制系统。
结构如图所示:
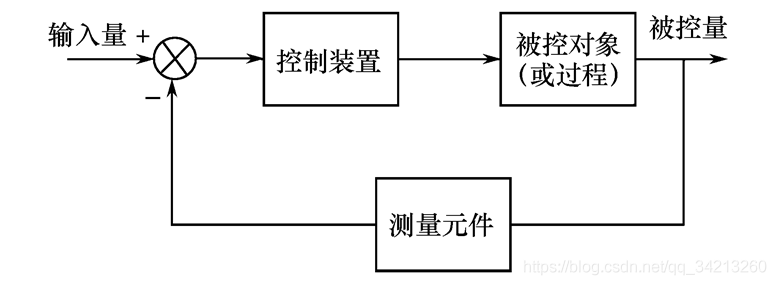
把控制系统输出量的一部分或全部,通过一定方法和装置反送回系统的输入端,然后将反馈信息与原输入信息进行比较,再将比较的结果施加于系统进行控制,避免系统偏离预定目标。闭环控制系统利用的是负反馈。
在反馈控制系统中,不管出于什么原因(外部扰动或系统内部变化),只要被控制量偏离规定值,就会产生相应的控制作用去消除偏差。
应用:
自动调温空调(当环境温度高于设定温度时,空调制冷系统自动开启,调定室温到设定值)、电饭锅自动保温、电冰箱温度控制系统、抽水马桶等。
PID控制原理
PID,它是闭环控制算法中最简单的一种。它通过三种简单的控制算法(即比例,积分,微分)的组合可有效地纠正被控制对象的偏差,从而使其达到一个稳定的状态。
P 比例调节
当距离目标越大时,调节作用越激进,当比较接近目标时,P的控制作用就比较小。越接近目标,P的作用越温柔。
特点:
简单、快速。
比例系数:
增大可以加快响应速度,减小系统稳态误差,提高控制精度。但是 过大会产生较大超调,甚至导致不稳定;若 取得过小,能使系统减少超调量,稳定裕度增大,但会降低系统的调节精度,使过渡过程时间延长。
比例响应:
比例模块仅仅取决于设定值和过程变量之间的差值。这个差值被称为“误差”。比例增益 (Kc)决定了输出响应对误差信号的比例。例如,如错误项的幅值为10,则比例增益为5将产生比例响应为50。一般情况下,增加比例增益将提高控制系统响应的速度。但是,如果比例增益太大,过程变量会出现振荡。如果继续增加Kc,系统振荡会越来越大,使得系统变得不稳定,以至于超出控制。
调节原理:
通常在控制的初始阶段,取较大的 ,以加快系统的响应速度,减小上升时间;在控制过程中期,适当减小 ,以减小系统超调;而到过渡过程的后期,为了保证系统的快速响应性能和稳态精度,应适当增大 。
I 积分调节
前辈科学家们想到的方法是真的巧妙,设置一个积分量,只要偏差存在,就不断地对偏差进行积分(累加),并反应在调节力度上。
作用:
主要用于消除静差提高系统的无差度,适用于有自平衡性的系统。
积分系数:
加大积分系数 有利于减小系统静差,但过强的积分作用会使超调量加剧,甚至引起振荡;减小积分系数 虽然有利于系统稳定,避免振荡,减小超调量,但又对系统消除静态误差不利。
积分响应:
积分模块将一段时间内的误差相加。即使是一个很小的误差,也会让积分响应缓慢增加。积分响应会根据时间持续增加,除非误差为0。因此,积分响应的目的在于将稳定状态的误差保持在0。稳定状态误差是过程变量和设定值之间的差值。当积分操作满足了控制器的条件,而控制器还未将误差保持在0时,会产生一种称为积分饱和的现象。
调节原理:
通常在调节过程初期阶段,为防止由于某些因素引起的饱和非线性等影响而造成积分饱和现象,从而引起响应过程的较大超调量,积分作用应弱些,而取较小的 ;在响应过程中期,为避免对动态稳定造成影响,积分作用应适中;在过程后期,应取较大的 值以减小系统静差,提高调节精度。
D 微分调节
我们需要一个控制作用,让被控制的物理量的“变化速度”趋于0,即类似于“阻尼”的作用。
作用:
主要是针对被控对象的惯性改善动态特性,它能给出响应过程提前制动的减速信号。它有助于减小超调,克服振荡,使系统趋于稳定;同时加快系统的响应速度,减小调节时间,从而改善了系统的动态特性。
微分响应:
如果过程变量快速增加,微分分量会导致输出减少。微分响应与过程变量的变化率之间成比例关系。增加微分时间(Td)会使控制系统对误差的反应更加剧烈,也会增加整个控制系统的响应时间。大多数实用控制系统使用非常小的微分时间(Td),因为微分响应对过程变量的噪声特别敏感。如传感器反馈信号中有噪声或控制循环速率太低,微分响应会使控制系统变得不稳定
调节原理:
若增加微分作用 ,有利于加快系统响应,使超调量减小,增加稳定性,但也会带来扰动敏感,抑制干扰能力减弱,若 过大则会使响应过程过分提前制动从而延长调节时间;反之,若 过小,调节过程的减速就会滞后,超调量增加,系统响应变慢,稳定性变差。
因此,对于时变且不确定系统, 不应取定值,应适应被控对象时间常数而随即改变。对于这类系统,在响应过程初期,适当加大微分作用可以减小甚至避免超调,在响应过程中期,由于对 的变化很敏感,因此 应小些,且保持不变;在调节过程后期, 要再小些,从而减弱过程的制动作用,增加对扰动的抑制能力,使调节过程的初期因 较大而导致的调节时间增长得到补偿。
PID控制器的参数整定
PID控制器的参数整定是控制系统设计的核心内容。它是根据被控过程的特性确定PID控制器的比例系数、积分时间和微分时间的大小。PID控制器参数整定的方法很多,概括起来有两大类:
- 理论计算整定法
它主要是依据系统的数学模型,经过理论计算确定控制器参数。这种方法所得到的计算数据未必可以直接用,还必须通过工程实际进行调整和修改。 - 工程整定方法
它主要依赖工程经验,直接在控制系统的试验中进行,且方法简单、易于掌握,在工程实际中被广泛采用。PID控制器参数的工程整定方法,主要有临界比例法、反应曲线法和衰减法。三种方法各有其特点,其共同点都是通过试验,然后按照工程经验公式对控制器参数进行整定。但无论采用哪一种方法所得到的控制器参数,都需要在实际运行中进行最后调整与完善。现在一般采用的是临界比例法。
PID调试一般原则
- 在输出不振荡时,增大比例增益P。
- 在输出不振荡时,减小积分时间常数Ti。
- 在输出不振荡时,增大微分时间常数Td。
总结
PID控制算法是可靠且简便的控制算法,在业内广泛使用。该算法灵活度高,在各种应用中表现优异,这也是多年来继续使用该算法的主要原因之一。
参考资料:
[PID算法](https://baike.baidu.com/item/PID算法/4660106 )
[PID理论详解](https://www.ni.com/zh-cn/innovations/white-papers/06/pid-theory-explained.html )
[一文搞懂PID控制算法](https://zhuanlan.zhihu.com/p/347372624 )


