王树森Attention与Self-Attention学习笔记
Seq2Seq + Attention
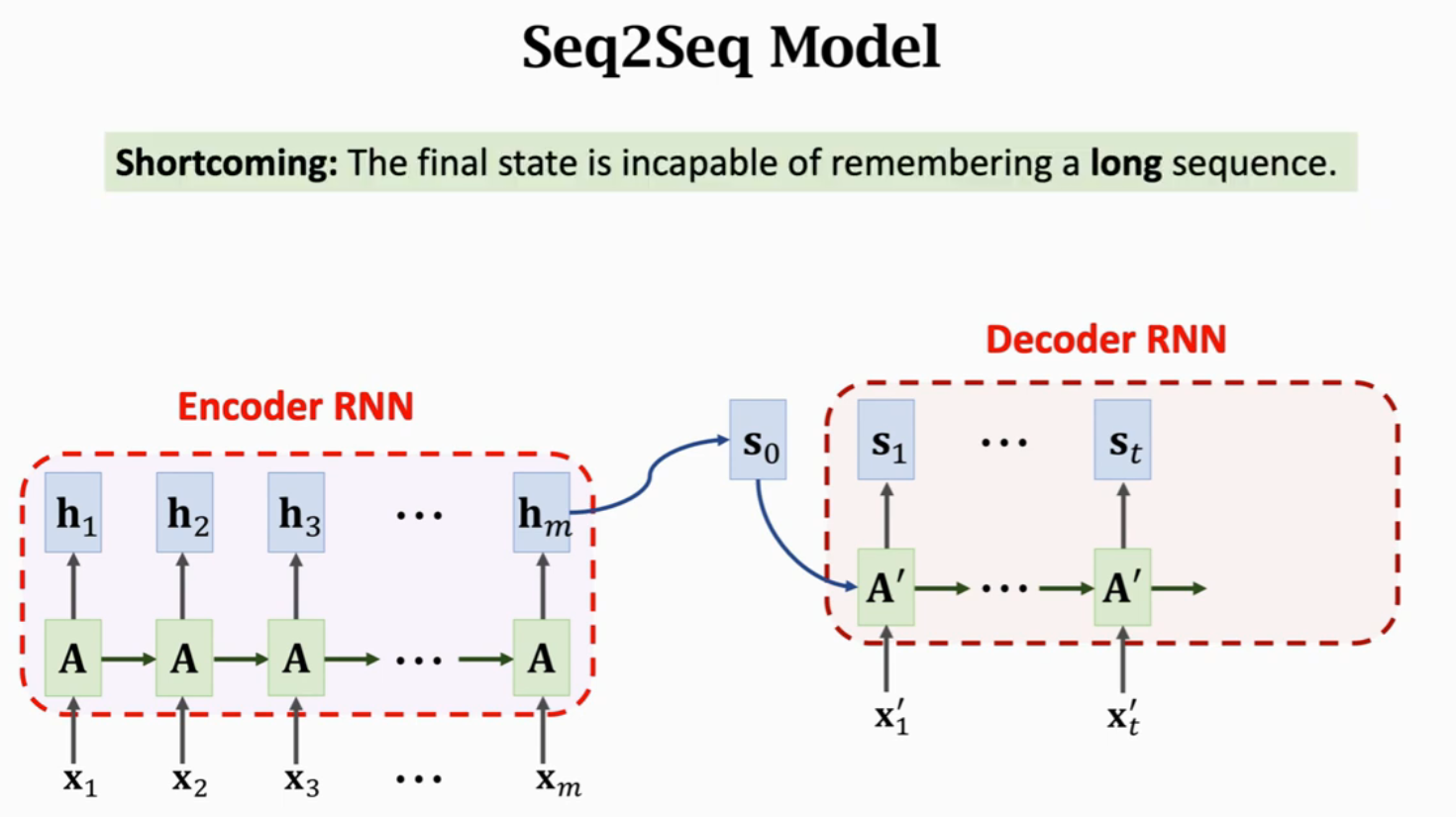
Seq2Seq模型,有一个Encoder和一个Decoder,默认认为Encoder的输出状态h_m包含整个句子的信息,作为Decoder的输入状态s_0完成整个文本生成过程。这有一个严重的问题就是,最后的状态不能记住长序列,也就是会遗忘信息,那么Decoder也就无法获得此信息。
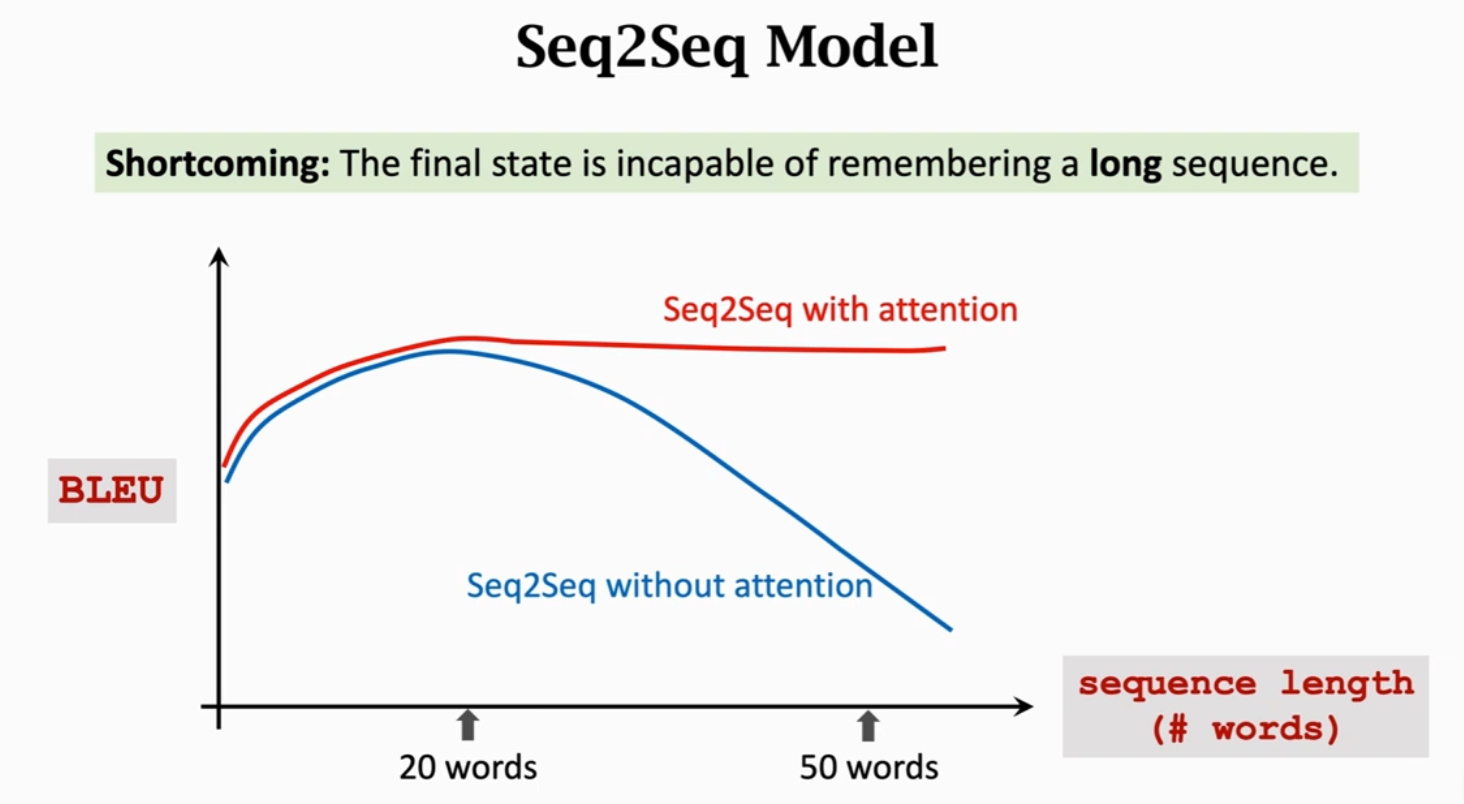
用传统的Seq2Seq模型,当句子长度超过20个单词是,BLEU Score(机器翻译评价指标)就会下降;但是如果用上Attention,就会如下图红色曲线一样,即使输入序列很长也能保持较高的准确率。
使用Attention解决机器翻译的原文为:Bahdanau, Cho, & Bengio, Neural machine translation by jointly learning to align and translate. In ICLR, 2015.
Attention能够极大提升Seq2Seq模型的准确率;用了Attention,Decoder每次更新状态的时候都会看一下Encoder的所有状态,这样子就不会遗忘了;Attention还可以告诉Decoder应该关注Encoder的哪个状态,这就是Attention名字的由来。Attention有一个极大的缺点是,计算量很大。
- Attention tremendously improves Seq2Seq model
- With attention, Seq2Seq model does not forget source input
- With attention, the decoder knows where to focus
- Downside: much more computation
Attention的原理
Attention使用\(c_i\)整合\(h_1, h_2, ..., h_m\)的信息,因此Attention机制可以解决LSTM遗忘的问题。
\(c_0 = \alpha_1h_1 + \alpha_2h_2 + ... + \alpha_mh_m\),其中,\(\alpha_i\)表示\(h_i\)和\(s_0\)的相关性,称为权重。

相关性的计算方法有两种:
-
方法一(Used in the original paper)
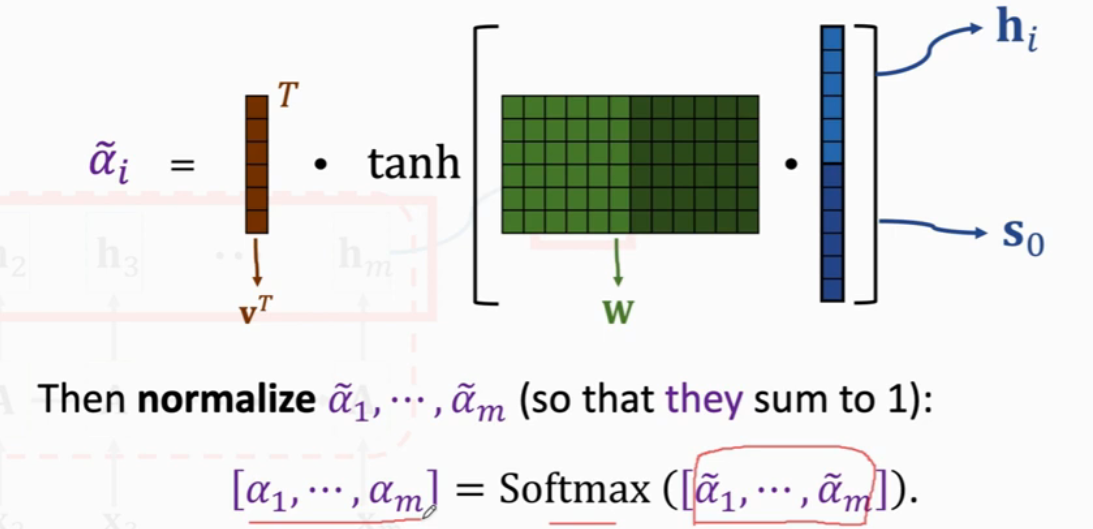
求\(h_i\)和\(s_0\)的相关性,将\(h_i\)和\(s_0\)进行Concatenate,然后乘一个参数矩阵\(W\),结果进行\(tanh\)约束到(-1, 1)之间,然后再乘以一个\(v^T\),并对得到的结果进行Softmax处理。
-
方法二(more popular,the same to Transformer)
求\(h_i\)和\(s_0\)的相关性,分为三步进行计算:
- Linear maps
- \(k_i = W_K · h_i\)
- \(q_0 = W_Q · s_0\)
- Inner product
- \(\widetilde{\alpha_i} = k^T_{i}q_0\)
- Normalization
- \([\alpha_1, ..., \alpha_m] = Softmax([\widetilde{\alpha_1}, ... \widetilde{\alpha_m}])\)
计算得到\(c_0\)后,将\(A'\)的三个输入进行concatenate,作为输入得到状态\(s_1\)。每一个状态\(s_i\)对应一个Context向量\(c_i\)来表示\(s_i\)与\(H\)的相关性。
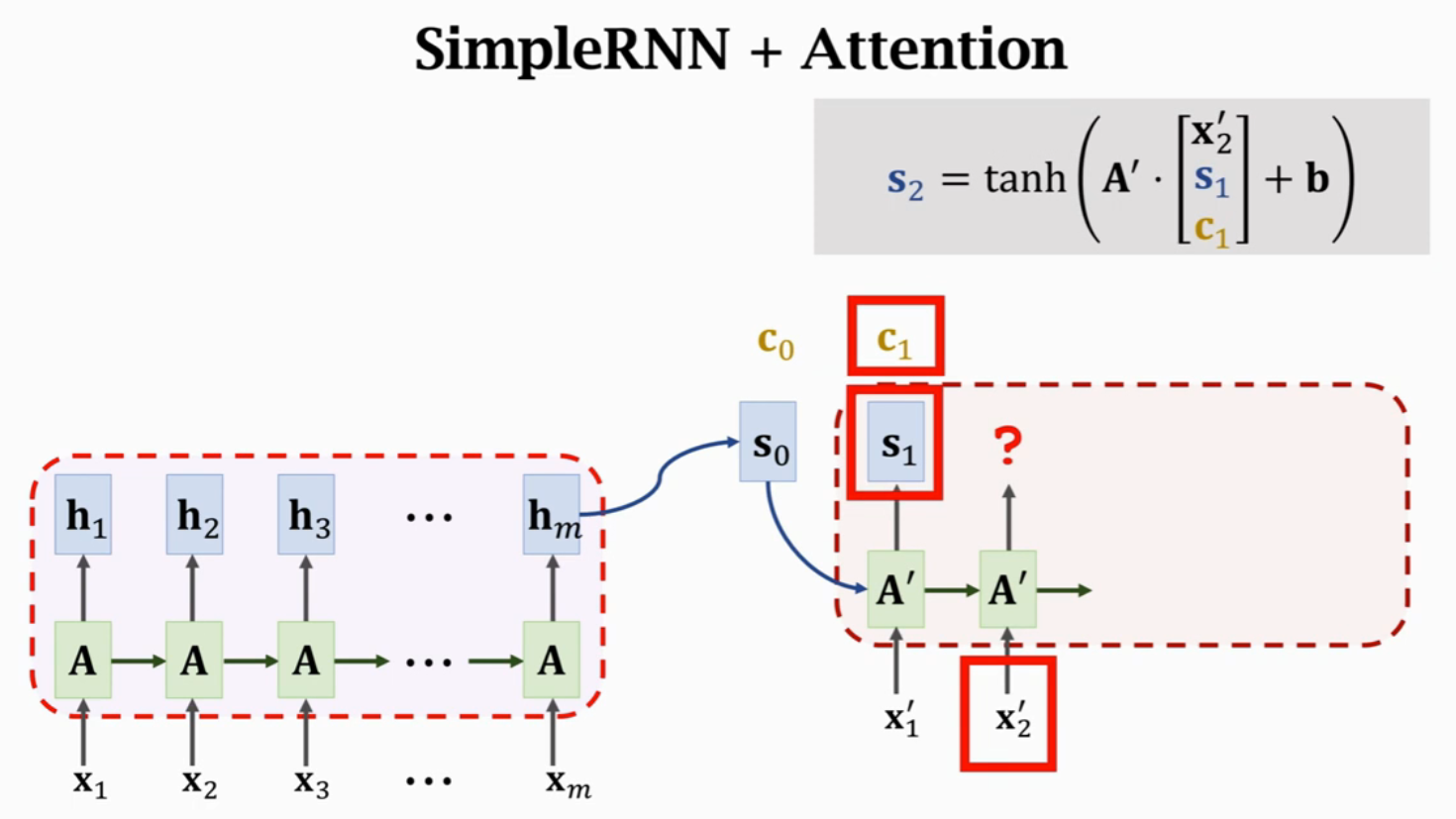
假设Encoder有m步,Decoder有t步,就需要计算mt次权重,每次权重计算都要计算m个\(\alpha\)的值。所以,Attention的时间复杂度是mt,也就是Encoder和Decoder状态数量的乘积。
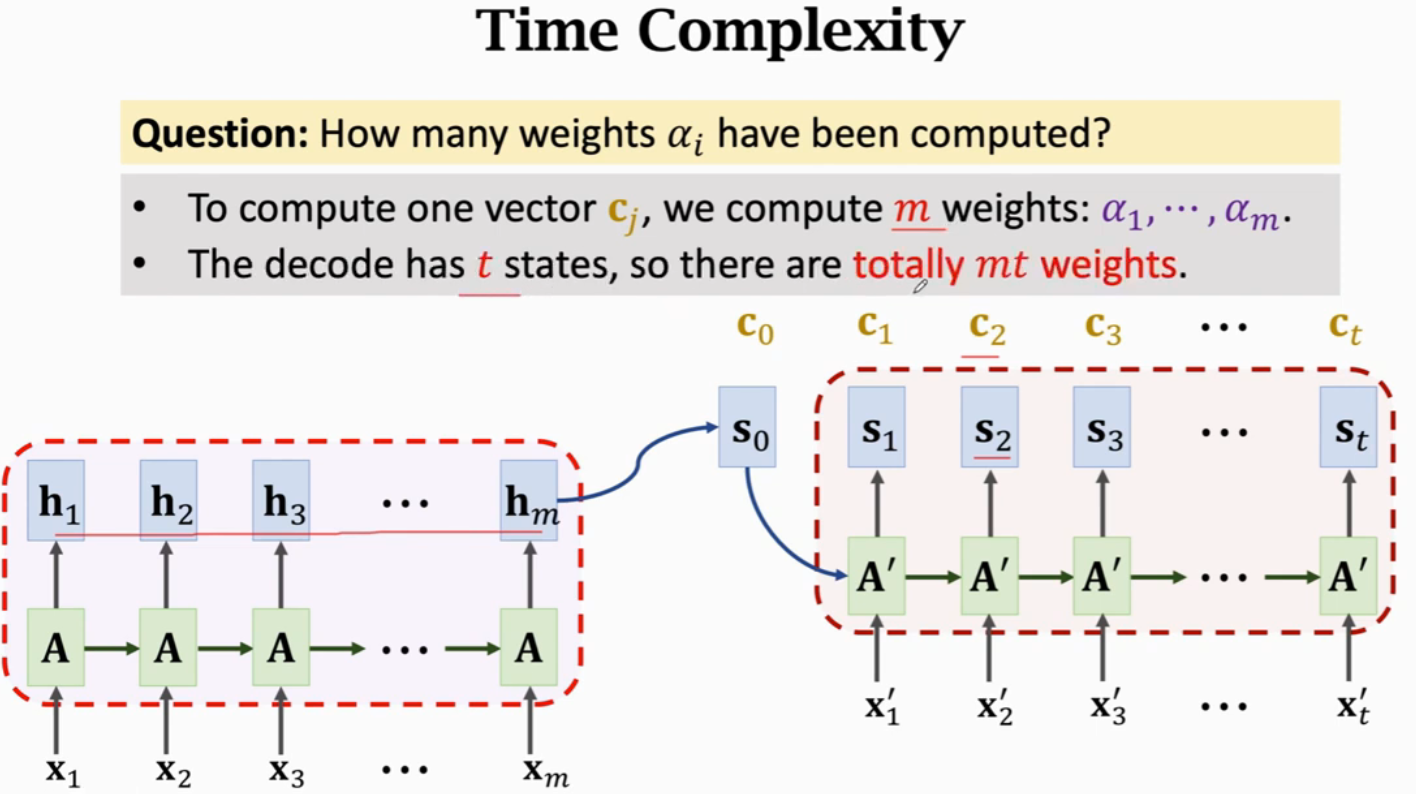
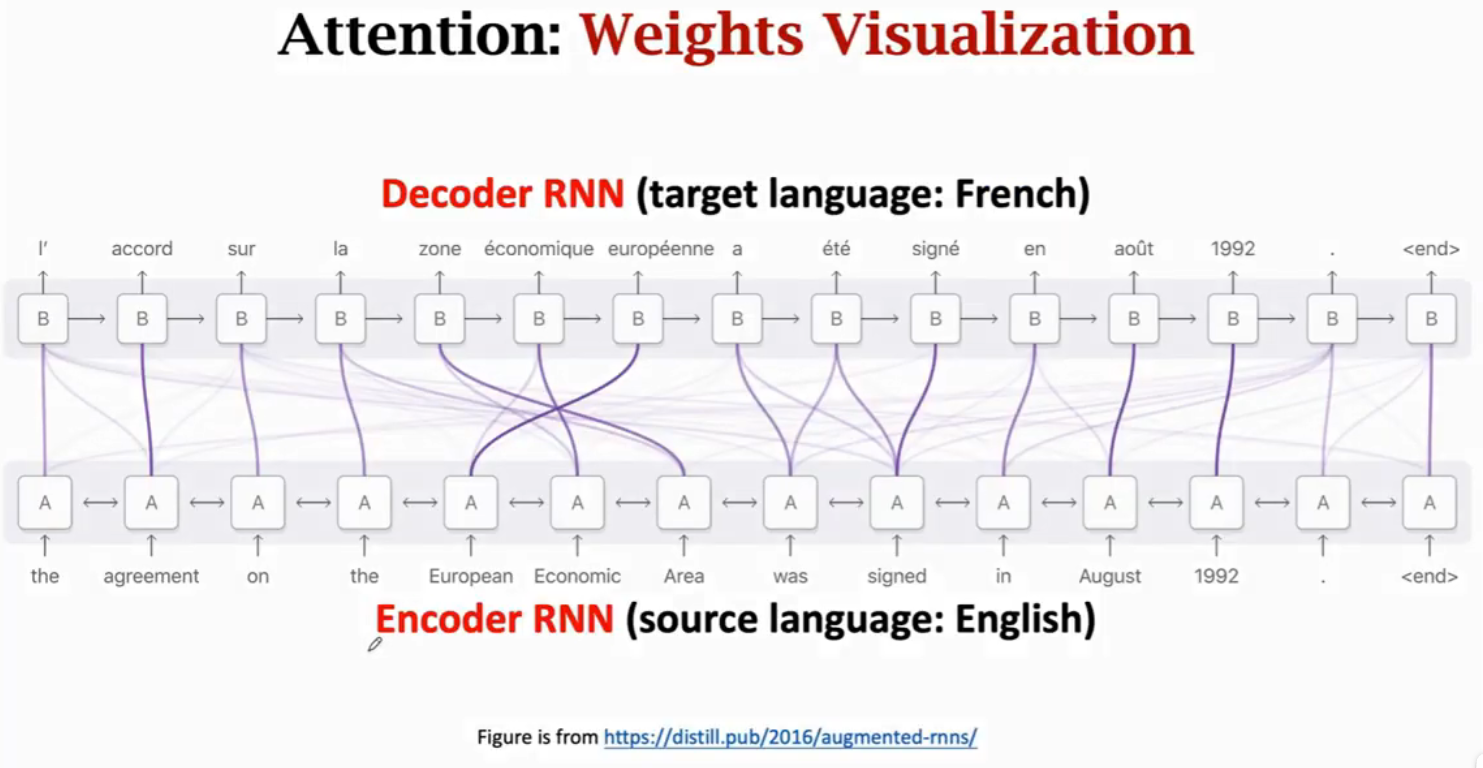
Attention在机器翻译任务的可视化,可以看到Decoder与Encoder的每个状态都相关,但是会重点关注某个或某些状态。
Summary
优点:
- Standard Seq2Seq model:decoder只关注其当前状态
- Attention:decoder还会关注encoders的所有状态解决遗忘问题并且告诉decoder哪里需要重点关注
缺点:高时间复杂度(假设源序列的长度为m,目标序列的长度是t)
- Standard Seq2Seq:\(O(m + t)\)
- Seq2Seq + attention:\(O(mt)\)
Self Attention
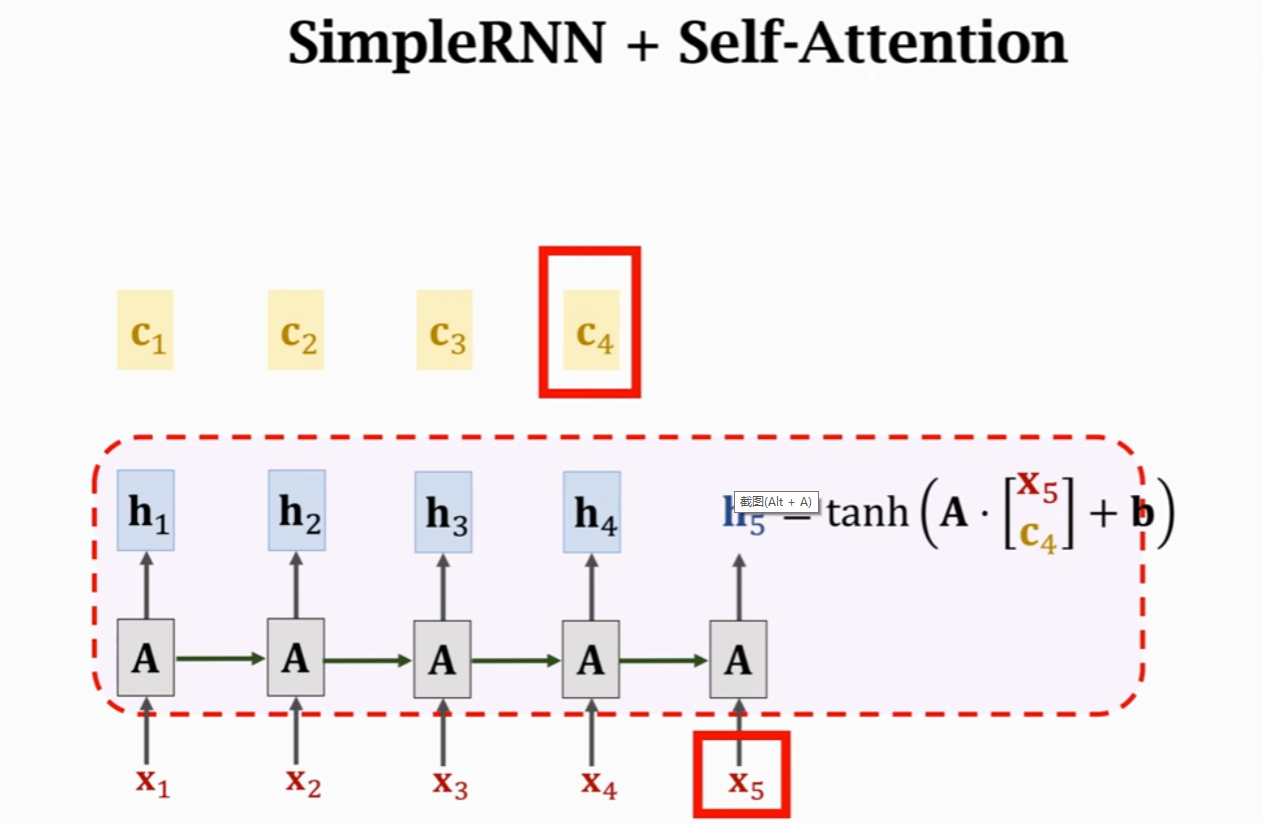
之前RNN里面,使用\(h_4\)和\(x_5\)计算得到\(h_5\),使用self-attention机制,当前状态\(h_5\)的计算依赖由\(h_4\)变为\(c_4\)。\(c_4 = \alpha_1h_1 + \alpha_2h_2 + \alpha_3h_3 + \alpha_4h_4\),其中,\(\alpha_i\)计算的是\(h_4\)与\(h_i\)之间的相关性,计算方式前面已经讲过。因为这里会计算自己与自己的相关性,因此称为self-attention。
-
SimpleRNN与Attention当前状态计算对比
SimpleRNN状态\(h_5\)的计算:
\(h_5 = tanh(A·{x_5\brack h_4} + b)\)
Self-Attention状态\(h_5\)的计算:
\(h_5 = tanh(A·{x_5\brack c_4} + b)\)
Reference

关注我的公众号 不定期推送资讯,接受私信许愿


