算法笔记:一文解决数组类型算法题(1)
本文主要介绍数据结构中的数组,以及LeetCode题库下面相关题型的分类和解法套路。
数组理论概述
定义
数组是存储在一块连续内存上的,由相同元素集合组成的数据结构。利用索引来计划其中具体元素的存储位置$^1$。
如图所示,该图代表一个连续数组,其实的具体的元素存储位置通过数组首地址加上索引的得出。
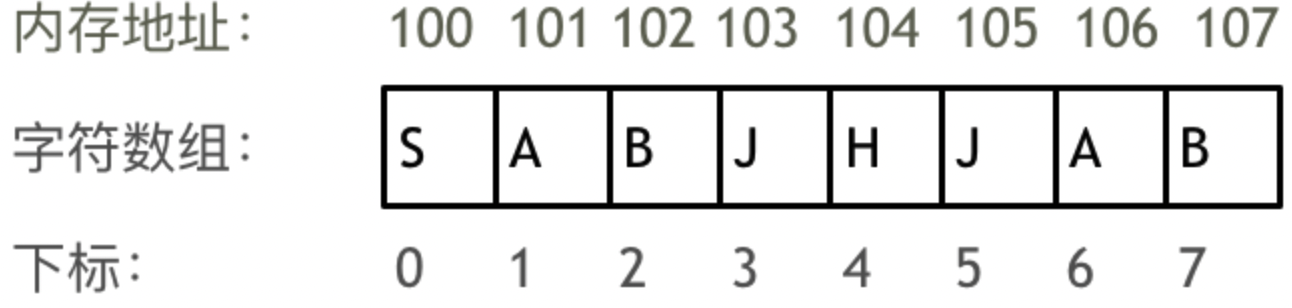
总的来讲,数组属于数据结构与算法的三要素里面的**线性结构**,使用连续内存空间存储元素,数组元素之间的也有一对一的逻辑关系。
数据结构与算法的三要素
数据结构与算法的三要素,分别为逻辑结构、存储结构与运算。
- 逻辑结构
- 概述:指的是数据元素之间的逻辑关系(eg:一对一、一对多、多对多)
- 特点:与数据存储结构无关,是独立于计算机的
- 分类:
- 线性结构(一对一)
- 线性表
- 栈
- 队列
- 数组
- 非线性结构(一对多、多对多)
- 集合
- 树 (1 vs n)
- 图 (n vs n)
- 线性结构(一对一)
- 存储结构
- 概述:数据结构在计算机中的表示(映像),又称物理结构
- 特点:
- 是数据元素的表示和元素之间关系的表示
- 存储结构用计算机语言实现逻辑结构,它依赖于计算机语言
- 分类:
- 顺序存储
- 概述:把逻辑上相邻的元素存储在物理位置上也相邻的存储单元中,元素之间的关系由存储单元的邻接关系来体现
- 优点:可以实现随机存取,每个元素占用最少的存储空间
- 缺点:智能使用相邻的一整块存储单元,因此可能产生较多的外部碎片$^2$
- 链式存储
- 概述:不要求逻辑上相邻的元素在物理位置上也相邻,借助指示元素存储地址的指针来表示元素之间的逻辑关系
- 优点:不会出现碎片现象,能够充分利用所有存储单元
- 缺点:每个元素因存储指针而占用额外存储空间,且智能实现顺序存储
- 索引存储
- 概述:在存储元素信息的同时,还建立附加的索引表
- 优点:检索速度快
- 缺点:
- 附加的索引表占用额外存储空间
- 增加和删除数据时也要修改索引表,会花费更多的时间
- 散列存储
- 概述:根据元素的关键字直接计算出该元素的存储地址,又称哈希(Hash)存储
- 优点:检索、增加和删除结构操作都很快
- 缺点:若散列函数不好,责可能出现元素存储单元冲突,而解决散列冲突会增加时间和空间开销
- 顺序存储
- 运算
- 指的是施加在数据上的原酸包括运算的定义和实现
- 运算的定义是针对逻辑结构提出的,指出运算的功能
- 运算的实现是针对存储结构提出的,指出运算的具体操作步骤
数组的使用
通过上面的介绍,我们大致了解了数组在数据结构与算法的定义和位置。
接下来本小节主要介绍数组在最常用的c++和Java语言中的使用方法。
Java中的数组使用
在Java语言中创建一个数组需要三步:
- 声明数组的名字和类型;
- 创建数组;
- 初始化数组。
声明并初始化一个数组示例:
double[] a; // 声明数组
a = new double[N]; // 创建数组
for(int i = 0; i < N; i++){
a[i] = 0.0; // 初始化数组
}
// 声明并初始化(简化写法)
double[] a = new double[N];
// 二维数组定义并初始化
double[][] a = new double[M][N];
⚠️注意: 在Java中,整数类型(byte、short、int、long)默认初始化值为0,浮点类型(float、double)初始化默认值为0.0,字符类型(char)初始化默认值为/u0000,布尔类型默认初始化值为false。
C++中的数组使用
在C++语言中创建一个数组步骤同Java一致,这里就不再赘述。
这里主要介绍C++中的两种数组定义和使用方法。
数组
在C++里面,既可以通过最普通的方式定义数组,也可以利用C++具备的指针可操作性定义和操作数组。
// 声明数组
int a[N];
// 声明并初始化;
int a[] = {1,2,3,4,5};
// 多维数组的创建并初始化
char daytab[2][13] = {{0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31}, {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31}};
⚠️注意:在C++中数组定义和Java中定义的区别,前者是在变量后面加中括号,后者是在类型关键字后面加中括号。
向量
向量这里主要指的是来自于stl库<vector>里面的用法$^3$;
// 声明向量
vector<int> a;
// 声明并初始化向量 arg1:向量长度, arg2:自定义初始化值(可选)
vector<int> a(arg1, arg2);
// 通过一个迭代器数组元素进行元素初始化
vector<int> a(it.begin(), it.end());
// 直接复制另一个相同元素类型的向量初始化
vector (const vector& x);
⚠️注意:使用第一种默认声明向量的方法时,不能一开始就通过下标索引操作向量,例如
a[1],这样会报错。要想直接使用索引操作,需要对向量进行初始化,或者声明长度,也就是说要使用下面的三种声明方式。
数组经典题型分类
本小节主要对于数组类型下面的LeetCode算法题型进行一个分类和具体的套路总结。
二分查找
说明
该类题一般呈现几个特点,要么是要求O(logn)时间复杂度在数组中查找目标位置,要么就是利用二分查找解决平方根问题。
方法
二分查找模版
int binarySearch(vector<int>& nums, int target) {
int low = 0, high = nums.size() - 1;
int mid;
while(low <= high){
mid = low + ((high - low) >> 1);
if(nums[mid] < target) low = mid + 1;
else if(nums[mid] > target) high = mid - 1;
else return mid;
}
return -1;
查找大于等于大于target的下标
int binarySearch(vector<int>& nums, int target){
int low = 0;
int high = nums.size() - 1;
while(low <= high){
int mid = low + ((high - low) >> 1);
if(nums[mid] >= target){
high = mid - 1;
}else{
low = mid + 1;
}
}
return low;
}
相关题型
| 编号 | 标题 | 难度 | 通过率 |
|---|---|---|---|
| 704 | 二分查找 | 简单 | 54.50% |
| 35 | 搜索插入位置 | 简单 | 45.10% |
| 34 | 在排序数组中查找元素的第一个和最后一个位置 | 中等 | 42.30% |
| 69 | x 的平方根 | 简单 | 38.80% |
| 367 | 有效的完全平方数 | 简单 | 44.90% |
双指针
说明
该类题型主要是对于数组的要求在O(n)时间下面的元素移动和删除操作。
方法
常见定义1
int i = 0, j = nums.size() - 1;
while(i <= j){
if(nums[i] == val){
nums[i] = nums[j--];
}else{
i++;
}
}
常见定义2
int i = 0, j = 1, n = nums.size();
while(j < n){
if(nums[i] != nums[j]){
nums[++i] = nums[j];
}
j++;
}
相关题型
| 编号 | 标题 | 难度 | 通过率 |
|---|---|---|---|
| 27 | 移除元素 | 简单 | 59.50% |
| 26 | 删除有序数组中的重复项 | 简单 | 54.40% |
| 283 | 移动零 | 简单 | 64.10% |
| 844 | 比较含退格的字符串 | 简单 | 48.90% |
| 977 | 有序数组的平方 | 简单 | 68.90% |
滑动窗口
说明
该类题的特点就是求的都是基于数组连续子序列的求值或长度最大最小,或者就是判断子字符串排列比较。
方法
for(int i = 0, j = 0; j < fruits.size(); j++){ // 【1】定义滑口的窗口起始和结束索引
basket[fruits[j]] ++; //【2】进入窗口操作
len++;
while(basket.size() > 2){ //【3】明确滑动窗口起始索引的变化条件
basket[fruits[i]]--;
if(basket[fruits[i]] == 0) basket.erase(fruits[i]);
i++;
len--;
}
if(res < len) res = len; //【4】
}
滑动窗口的三个重点
- 定义滑口的窗口起始索引和结束索引,这里的目的就是通过指针
j来遍历水果数组; - 进入窗口的元素操作,在这里就是将水果放入篮子里面;
- 明确起始索引变化的条件,在这里就是满足篮子元素大于2之后,就需要对最先进来的元素进行移除操作;
- 在求得滑动窗口后,比较每操作完成之后篮子内收集水果的最大数目
相关题型
| 编号 | 标题 | 难度 | 通过率 |
|---|---|---|---|
| 209 | 长度最小的子数组 | 中等 | 48.40% |
| 904 | 水果成篮 | 中等 | 43.60% |
| 76 | 最小覆盖子串 | 困难 | 44.70% |
| 567 | 字符串的排列 | 中等 | 44.20% |
| 438 | 找到字符串中所有字母异位词 | 中等 | 54.80% |
螺旋矩阵
说明
该类题,就是对一个二维矩阵进行顺时针遍历操作。
方法
int l = 0, r = n - 1, t = 0, b = n - 1; // 定义左右上下四个边界变量
int num = 1, tar = n * n;
while(num <= tar){
// 从左到右
for(int i = l; i <= r; i++) mat[t][i] = num++;
t++;
// 从上到下
for(int i = t; i <= b; i++) mat[i][r] = num++;
r--;
// 从右到左
for(int i = r; i >= l; i--) mat[b][i] = num++;
b--;
// 从下到上
for(int i = b; i >= t; i--) mat[i][l] = num++;
l++;
}
相关题型
| 编号 | 标题 | 难度 | 通过率 |
|---|---|---|---|
| 59 | 螺旋矩阵 II | 中等 | 75.60% |
| 54 | 螺旋矩阵 | 中等 | 49.10% |


 浙公网安备 33010602011771号
浙公网安备 33010602011771号