机器学习概述

本文主要是对于阅读周志明《智慧的疆界》的章节笔记总结

机器学习是什么？有什么价值？

要谈机器学习是什么？这里直接给出比较代表定义不断发展的机器学习定义。

1）司马贺：“机器学习就是让机器能够从历史经验中不断改善自身的过程”

2）汤姆·米切尔：“假设某项评价指标可作为系统性能的度量（Performance，简称P），而这个指标可以在某类任务（Task，简称T）的执行过程中随着经验（Experience，简称E）增加而不断自我改进的话，那么我们就称该过程‘Process＜P, T, E＞’是一种学习行为”。

3）李航：“机器学习 = 模型 + 策略 + 算法”

• 模型是指机器学习所要产出的内容，它一般会以一个可被计算的决策函数或者条件概率分布函数的形式存在。
• 策略是指要按照什么样的准则进行学习，具体一点是按照什么样的准则选择出最优的模型。
• 算法是指如何依靠历史数据，把正确的模型中涉及的未知参数都找出来。

它有什么价值呢？

• 让计算机参与任务思考和设计成为可能。
• 编写出可以“自发能够产生‘解决问题程序‘的程序“。

它能解决哪些问题？

人类认知世界的两种最基本手段是“演绎”和“归纳”，有什么样的工具、手段，就能解决什么样的问题，人类能够认知的知识的范围，是由这两种手段划定的。

人类的认识的知识可以划分为以下四个象限的知识。基于规则就是人类通过演绎（符号、规则）可以认识的知识，基于数据就是人类可以通过归纳（大数据、统计）可以认识的知识。

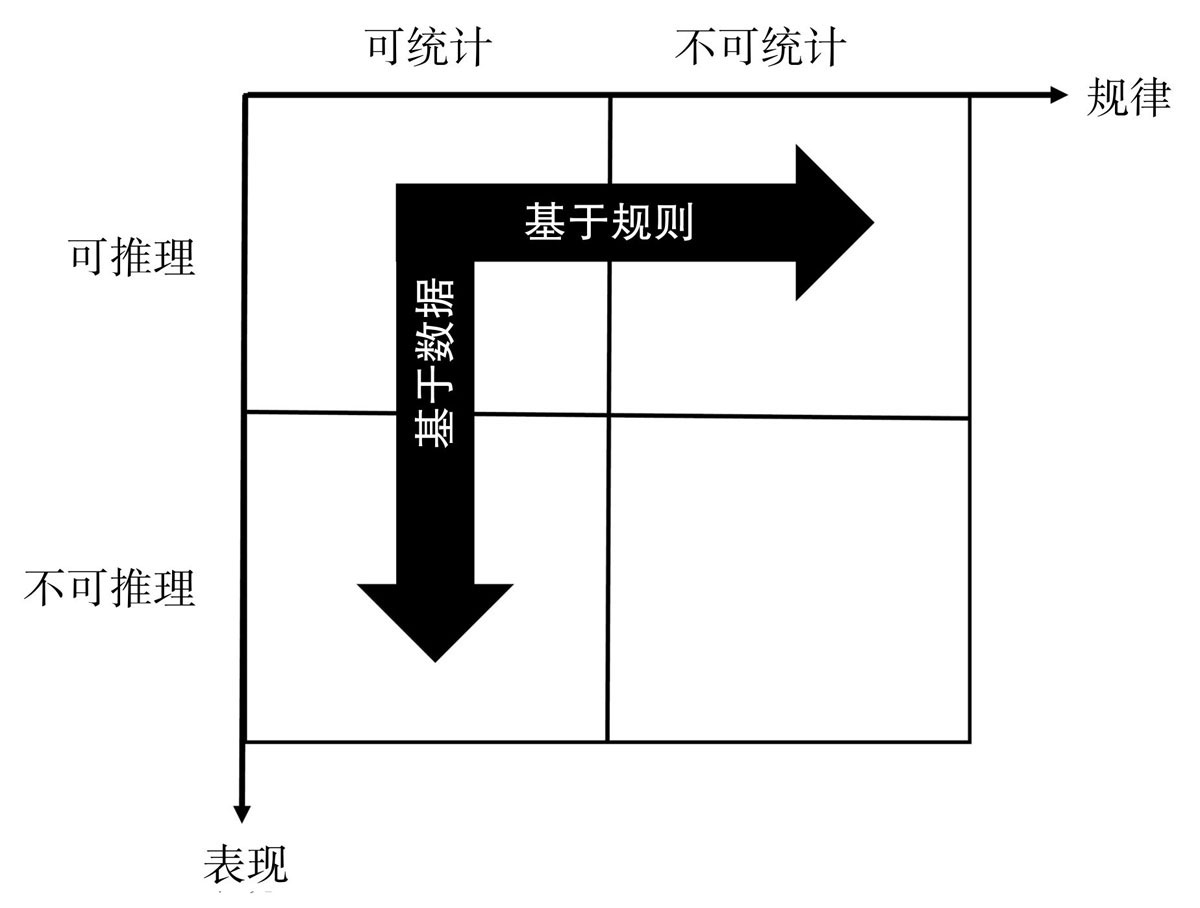
因此，机器学习可以解决的问题主要划分为以下四种：

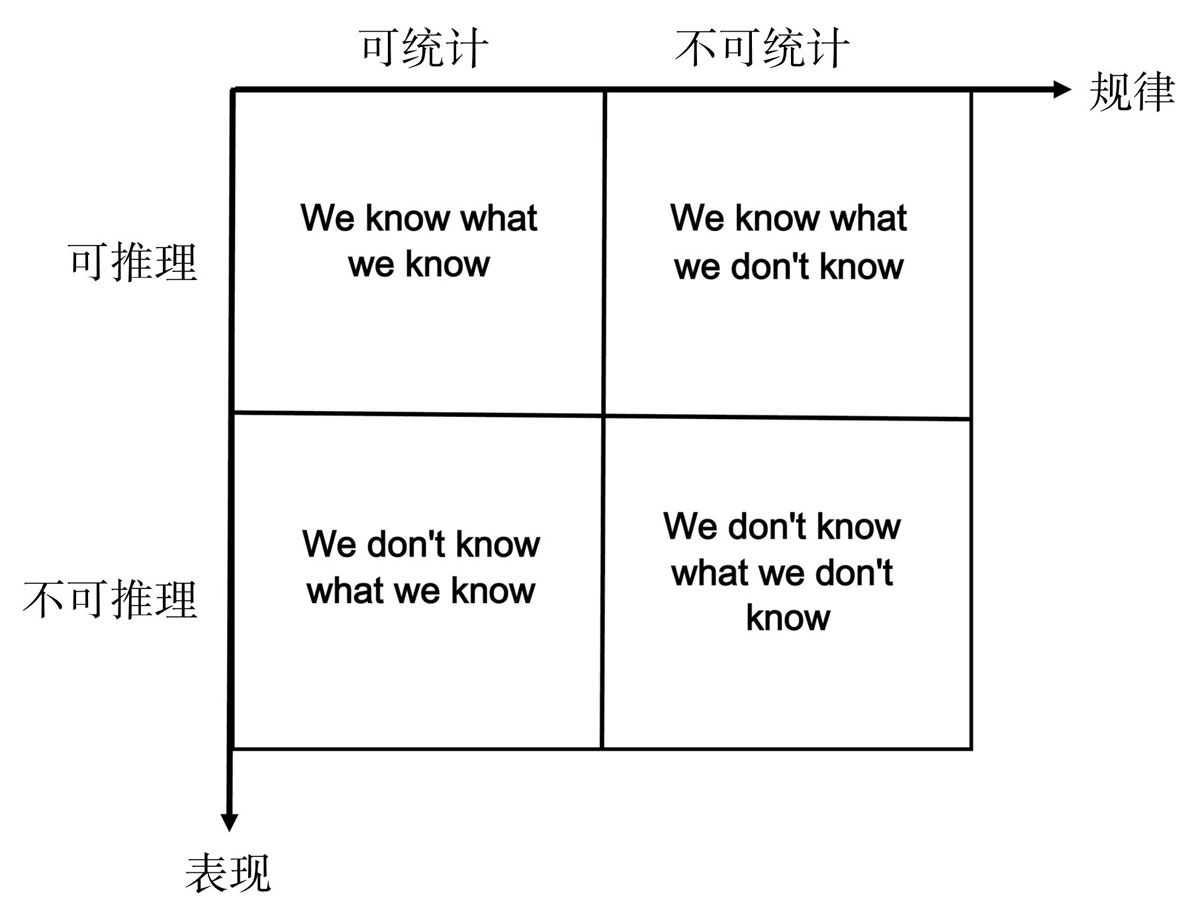
• 第一类问题（We know what we know）：对这种可推理可统计的问题，无论用何种方法，原则上我们都可以寻找到答案。
• 第二类问题（We know what we don't know）：对于能够通过已知规律推理得到未知现象的问题，例如我们身边的各种数学定理、宏观的物理定律都是依靠严格的逻辑推理得出的，我们知道了今天地球的位置、角度、速度、质量等，完全可以准确无误地预测出1000年之后地球的精确位置，这个预测依赖的就是根据人们已掌握的天体运行规律来推理得到的。
• 第三类（We don't know what we know）：即不知道规律，但可以根据已知现象的统计结果去推测未知现象的问题。
• 第四类（We don't know what we don't know）：这类问题我们既不知道它蕴含的规律，也没有办法统计出任何有规律的特征。

准确来讲，第四种是目前的机器还无法真正解决的问题，这对于人来讲都是需要“顿悟”才能明白的问题。因此，有学者感慨“每当一个问题被计算机解决了之后，大家就不再认为这个是人工智能了。”因此，这样也更加深刻理解人工智能，其实是一种具备人一样拥有“顿悟”能力的才算是真正的人工智能。

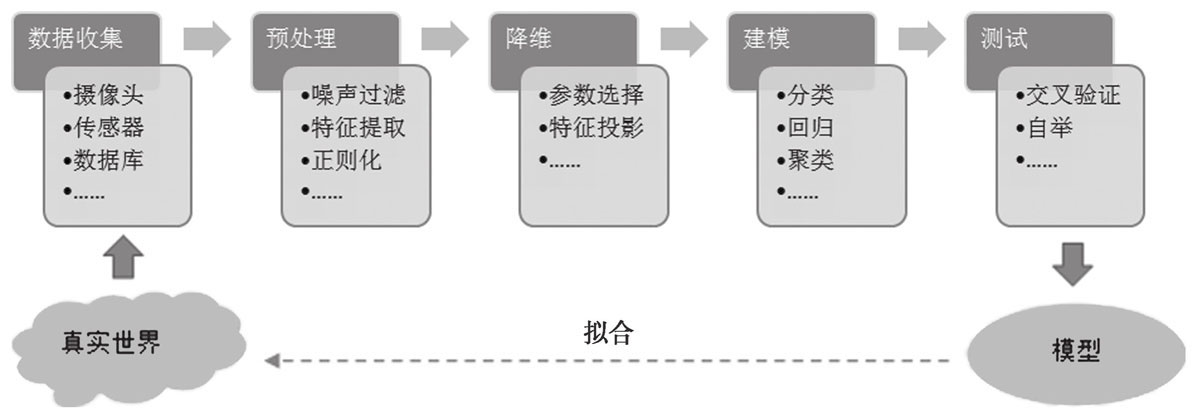
它会经过哪些步骤来解决这些问题？

机器学习就是从数据采集、预处理、选取特征、确定损失函数、解决欠拟合和过拟合，到最后通过优化算法获得模型的过程。

一些基本名词

• 模型：从形式上说，模型就是一个可被计算的、有输出结果的方法或函数，这个函数可能是有科学含义的，也可能没有任何含义，可能用于决策，也可能用于预测。
• 模型训练：是指从真实世界的一系列历史经验中获得一个可以拟合真实世界的决策模型。
• 样本：是一种包含了若干关于某些事实或者对象的描述的数据结构

机器学习三类任务类型

• 聚类：
  • 定义：是指机器通过训练集中获得的特征，自动把输入集合中的样本分为若干个分组（Cluster，簇，此处读者将其理解为“分组”即可），使得每个分组中存放具有相同或相近特征的样本。
  • 目的：聚类通常是为了发现数据的内在规律，将它们同类的数据放到一起，为进一步深入分析和处理建立基础。
• 分类和回归的异同
  • 都是根据样例训练集中得出的历史经验来推断新输入给模型的样本是否属于某一类。
  • 主要差别是，回归做的是定量分析，输出的是连续变量的预测，而分类做的是定性分析，输出的是离散变量的预测。
  • 分类的目的一般是用于寻找决策边界，用于做出决策支持，而回归的目标大多是希望找到与事实相符的最优化拟合，用于做事实模拟。

数据处理的两种手段

保证数据是正确的部分，称为“数据清洗”（Data Cleansing），而保证数据是合适的这部分，就称为“特征选择”（Feature Selection）。

数据清洗的常见操作：

• 数据集成，将多个数据源中获得的数据结合起来，形成一致的结构，存放在一个一致的数据存储中。
• 基础清洗操作，典型如对数据进行基本的去重过滤。
• 分层采样，对于样本数据较多，各样本之间差异较大的情况，会通过不同的办法保证采样平衡，抽出具有代表性的调查样本，增大各类型样本间的共同性。
• 数据分配，将数据集按照一定比例，分割为训练集、验证集、测试集等几部分，后续我们讲测试验证的时候会再介绍这些内容。
• 数据规范化，譬如将量纲表达式转化为纯量表达式（可简单理解成把数据“去掉单位”，譬如10厘米和1分米，归一化之后是一样的），然后缩放到同一数量级（典型的如0到1之间），提升指标之间的可比较性。
• 平滑化，缩小数据在统计下的噪声差异，典型的一种平滑化操作是分箱。分箱实际上就是按照属性值把样本划分到不同的子区间，如果一个属性值处于某个子区间范围内，就把该属性值放进这个子区间所代表的“箱子”内。在处理数据时采用特定方法分别对各个箱子中的数据进行处理。
• 数据填补，典型的如ID值生成、使用统计算法替换缺失的观察值等。

特征选择的两个纬度：

• 考虑特征的离散度：如果一个特征不发散，譬如说方差趋近于0，也就是各个样本在这个特征上基本上没有差异，这个特征对于样本的区分就没有什么意义。
• 考虑特征与目标的相关性：与目标相关性高的特征，更能作为分类决策的依据，肯定就应当优先选择，这里的关键是解决如何能判断出特征与目标的相关性。

泛化、误差及拟合

• “泛化能力”（Generalization Ability），就是机器学习算法对新鲜样本的适应能力，作为衡量机器学习模型的最关键的性能指标，性能良好的模型，就意味着对满足相同分布规律的、训练集以外的数据也会具有良好的适应能力。
• 误差（Error）＝偏差（Bias）+方差（Variance）+噪声（Noise）
  • 偏差的含义是指根据训练集数据拟合出来的模型输出结果与样本真实标记的差距。
  • 方差的含义是指给出同样数量，但内容发生了变动后的样本数据所导致的模型性能变化。方差大小的本质是描述数据扰动对模型输出结果所造成的影响。

一些定理原则

• “奥卡姆剃刀”法则（Occam's Razor，拉丁文为“lex parsimoniae”，含义为“简约法则”）：作指导决策的行之有效的经验法则。通俗地说，这条法则应用在机器学习领域中的含义是指：“如果有两个模型可以产生相同性能的预测结果，那选择较简单的那个会是更好的。”
• “没有免费的午餐定理”（No Free Lunch Theorem, NLFT）：如果一个算法对于某类型的问题比另外的算法效率高，那么它一定不具有普适性，一定存在另外某一类问题使得这个算法的性能低于随机选择的结果。具体问题具体分析。