决策树学习笔记
决策树
学习笔记
一. 基本流程
决策树(判定树)是一种常见的机器学习分类算法。(其中CART决策树也可以做回归)
直观的理解:决策树顾名思义是一种树结构的模型,所谓的决策是从根结点开始一步步走到叶子结点的这样一个过程,每进行一次划分(就是每个样本根据自己的某个属性选择走了哪条路)的过程。划分的目的是希望:越分越纯。
结构:一般包含一个根结点、若干个内部结点和若干个叶结点;判定测试序列:从根结点到某一叶结点的路径
- 根结点包含样本全集
- 叶结点对应于决策结果(好瓜)
- 其他每个结点对应于一个属性测试,每个结点包含的样本集合根据属性测试的结果被划分到子结点中
一个例子:
每个测试结果或是导出最终结论,或是导出进一步的判定问题,其考虑范围是在
上次决策结果的限定范围之内。(比如上面的例子中,在第二层最左面对样本根据根蒂进行划分时,划分的样本是第一次判断后判断色泽是青绿的这个范围内)
生成决策树的基本算法(分而治之):
(一个递归过程)首先生成node节点,先看下样本类别是不是相同,如果D中样本都是一类(比如说C类)的,那肯定就不用再细分了嘛,所以直接给它标签为类别C;
再看样本属性取值上能否区别开来,如果属性集为空或者样本在属性集上取值没有区别,也就是说没法根据属性进行分类了,那么就给它标签为D中样本数最多的类,这种情况利用了当前结点的后验分布;
样本类别也不同,也能在属性取值上区别开来,那就规规矩矩开始进行划分,选择一个最优化分属性,对于属性上的各种取值给一个分支。如果某一个分支的样本子集为空那么标记叶结点,标记为父结点中样本最多的类,这种情况把父结点的样本分布作为当前结点的先验分布。否则的话就调用自身接着往下生成。
决策树的训练与测试:
- 训练:生成决策树的过程
- 测试:抛给决策树一个例子,根据构造好的决策树从上到下走一遍对例子进行测试
测试是比较简单的,就根据模型往下走着预测就行,这一块主要讨论的是How to generate?在上面基本算法第8行提到选择最优划分属性,我们自然会想到,决策树划分属性的顺序可以变化吗?如何选择最优呢?
其实我们希望前面的一些结点可以产生较强的效果,进行大致的判断,后面的结点可以进行进一步的细化。
那么该选哪个特征呢?如何切分呢?哪个结点效果更强呢?
二.划分选择
我们用“熵”对纯度进行衡量,熵:表示随机变量不确定性的度量。
2.1 信息增益
选择最优划分属性时,希望随着划分过程不断进行,“纯度”越来越高。
这里用熵来作为衡量标准(熵越大意味着越混乱,越混乱意味着纯度越低)
信息熵:度量样本集合纯度最常用的一种指标。 当前样本集合D中第k类样本所占比例为,则D的信息熵定义为:
Ent(D)越小,D纯度越高。
从信息熵公式数学角度看待这个问题:
熵之所以用了log函数,是因为它不是说想看想样本的label本身存在的不确定性,而是想看多少个bit的玩意儿的不确定性带来了样本的不同个label的可能。举个投硬币的例子(用比特作为熵的单位),如果我们说硬币的结果组合有8种可能,正正正、负负负...,那么这个问题的熵是,不确定性是3,3个硬币的不确定性带来了这8种不同的结果。
但上面这个是等可能性下的,可能性不相等时,就拓展成了信息熵公式。
关于具体熵值和混乱程度的关系自己的想法:对于某两类样本(假设其比例和为a,即其中一类比例是x,另一类是(a-x)),可以通过简单的求导证明:当x=a或者0时,可以取得一个最小值,等于,当x=0.5a时,该式子取得最大值。也就是说对于任意两类,假设它俩所占比例和一定,它俩可以算为一类时(或者说一类存在样本中,一类不存在样本中对Ent(D)的贡献最少,而两者比例各自占一半对Ent(D)贡献最多)
最大值与最小值的情况:(纯度最大对应信息熵最小)
信息增益:表示特征X使得类Y的不确定性减少的程度。(分类后的专一性,希望分类后结果尽可能是同类在一块)
用属性a对样本集D进行划分后获得:
(ID3决策树学习算法使用的) 这里假设a有V个不同的取值,是D中所有在a上取值为的样本。一般而言,信息增益越大,意味着使用属性a来进行划分所获得的 “纯度提升” 越大,因此可以用它来进行划分属性选择。
多个属性均取得最大的信息增益,可任选其中之一作为划分属性。
基于信息增益生成的决策树:
局限性:对可取值数目较多的属性有偏好(每一类数目较少,更容易“纯”,例如将样本ID号作为一个属性加进去考虑)
2.2 增益率
增益率:可减少上述偏好可能带来的不利影响,定义如下:
IV(a)是属性a的“固有值”,a的可能取值数目越大,固有值通常也越大。(有的网课里称之为自身熵)
局限性:对可取数目较少的属性有所偏好。
C4.5算法采取策略:先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的。
2.3 基尼指数
CART:是一种决策树学习算法,分类和回归任务都可用。(使用基尼指数来选择划分属性)它的特点是一定生成的是二叉树,(左是右否)
基尼值(反映了从数据集D中随机抽取两个样本,其类别标记不一致的概率,值越小、数据集纯度越高):
基尼指数定义:
选择使得划分后基尼指数最小的属性作为最有划分属性。
三. 剪枝处理
(决策树学习算法通过主动去掉一些分支来对付“过拟合”的主要手段)
判断决策树泛化性能是否提升:使用性能评估方法
基本策略:
- 预剪枝
对结点划分前进行估计,边建立决策树边进行剪枝。
西瓜书中预剪枝例子(样本集和未剪枝决策树在西瓜书里,采用了留出法):
局限性:有些分支可能当前不能提升泛化性能,但是基于它的后续划分可能提高性能,所以存在”欠拟合“风险。 - 后剪枝
生成决策树后自底向上对非叶结点进行考察。
当剪枝不会带来验证集精度提高时,理论上可以不剪枝。但是根据奥卡姆剃刀准则,剪枝后的模型更好。
西瓜书中后剪枝例子:
优点:泛化性能往往由于预剪枝决策树
局限性:训练时间开销较大
四. 连续与缺失值
4.1 连续值处理
C4.5决策树算法采用二分法对连续属性进行处理(离散化)
给定样本集D和连续属性a,假定a在D上出现了n个不同的取值,将这些值从小到大排序,记为:{},考察包含n-1个元素的候选划分点集合:
选取最优划分点。(进行切分尝试,看哪个点切分使效果比较好)
也可将划分点设为该属性在训练集中出现的不大于中位点的最大值。
样本集D基于划分点t二分后的信息增益:
区别于离散属性:若当前结点划分属性为连续属性,该属性还可作为其后代结点的划分属性。
4.2 缺失值处理
需要解决的问题:
- 如何进行划分属性选择
- 丢与该属性上值缺失的样本,如何将其划分
核心就是引入权重
注意上面的公式是基于给定的样本集D和给定的属性a的。
:无缺失样本所占比例
:无缺失值样本中第k类所占的比例
:无缺失值样本中在属性a上取值的样本所占的比例
=1, =1
将信息增益计算式推广为:
若样本x在划分属性a上的取值已知,则划入对应子结点,样本权值保持为,否则将x划入所有子结点,且样本权值在与属性值对应的子结点中调整为.
(C4.5算法使用了上述方案)
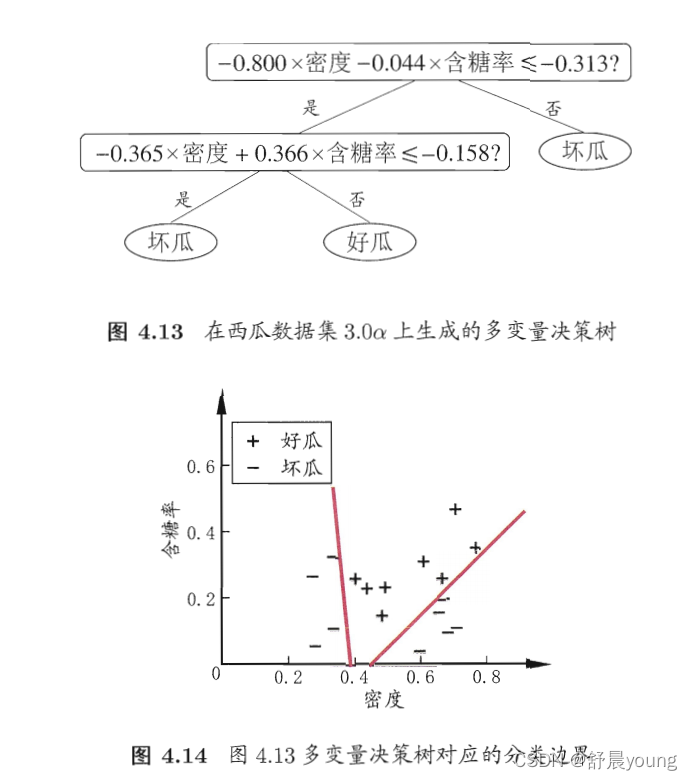
多变量决策树
对样本分类意味着在这个坐标空间寻找不同类样本之间的分类边界。
决策树形成的分类边界特点:轴平行(分类边界由若干个与坐标轴平行的分段组成)
多变量决策树:能实现“斜划分”甚至更复杂划分的决策树。非叶结点不再是仅对某个属性,而是对属性的线性组合进行测试,每个叶结点是形如的线性分类器。
补:
决策树除了应用于分类任务,还可以应用于回归任务。只不过后者不用熵值去考虑,用的是方差。



















【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 微软正式发布.NET 10 Preview 1:开启下一代开发框架新篇章
· 没有源码,如何修改代码逻辑?
· PowerShell开发游戏 · 打蜜蜂
· 在鹅厂做java开发是什么体验
· WPF到Web的无缝过渡:英雄联盟客户端的OpenSilver迁移实战