第四次实验

项目一

项目分析

-通过 邻接矩阵 实现无向图并保存边和顶点，实现添加以及删除结点的方法，添加和删除边的方法

• 方法包括实现size()和isEmpty()，广度优先迭代器，深度优先迭代器

• 广度优先迭代器以及深度优先迭代器在书本的417页给出了算法示例。

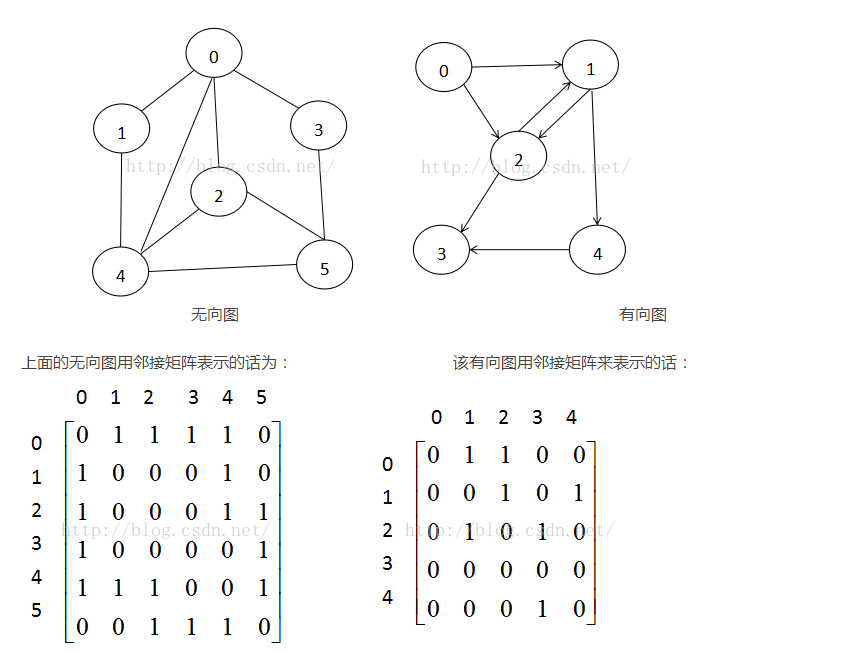
• 那么，什么是邻接矩阵呢？----邻接矩阵是表示图形中顶点之间相邻关系的矩阵，对于n个顶点的图而言，矩阵是的row和col表示的是1....n个点。对于无向图 如果顶点b1和b2是连接的，那么在二维矩阵中matrix[b1,b2]和matrix[b2,b1]位置的值置为1，如果是有向图b1指向b2，那么 matrix[b1,b2]=1,matrix[b2,b1]=0；下面用一个例子表示无向图和有向图的邻接矩阵；

• 这里有优秀博客的解释范例
  

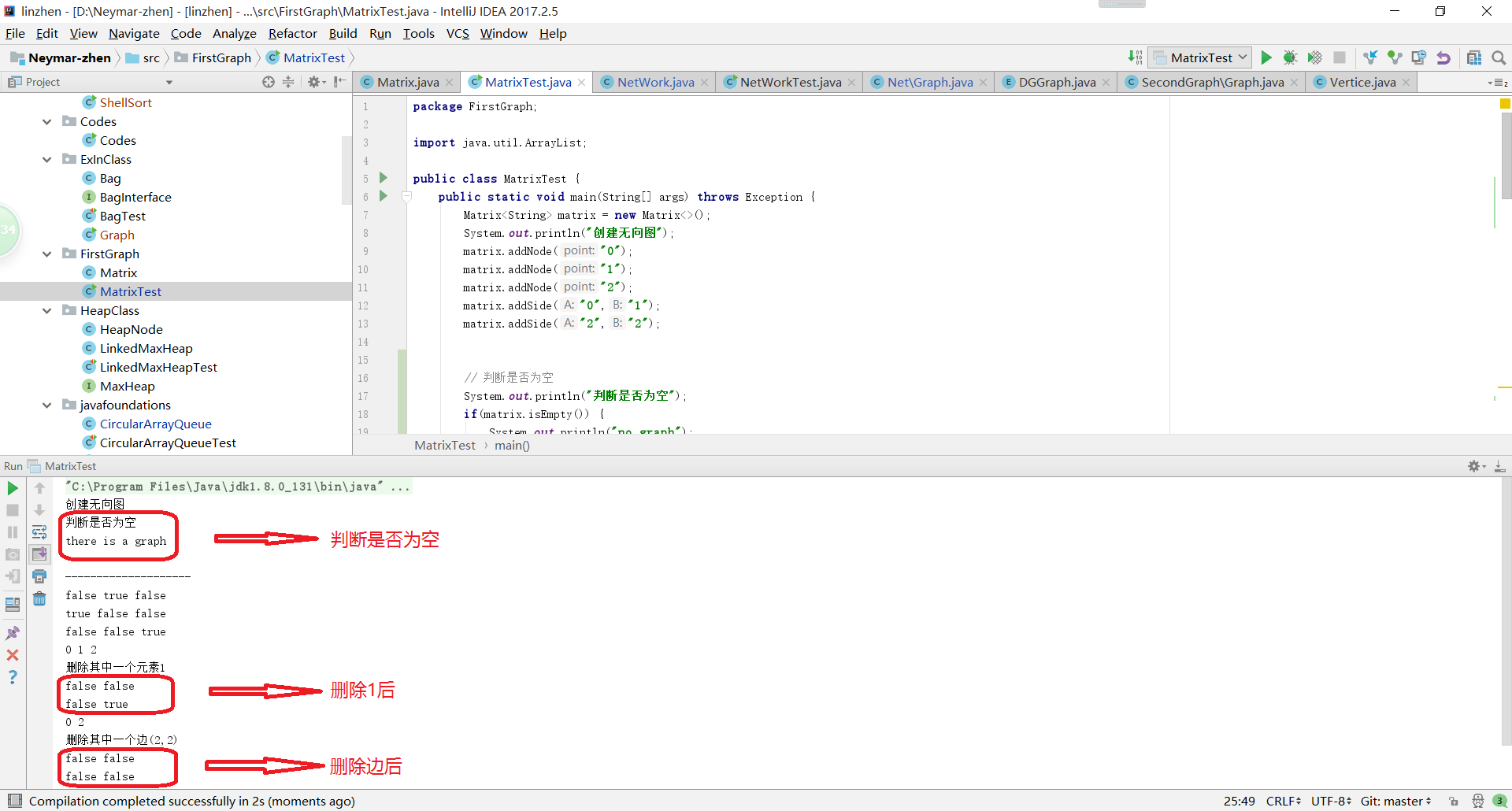
• 代码运行结果
  

项目二

项目分析

• 通过 十字链表 实现无向图，并将边和顶点保存，实现在添加和删除结点的方法，添加和删除边的方法

• 方法包括实现size()和isEmpty()，广度优先迭代器，深度优先迭代器

• 十字链表又是什么呢？-----十字链表（Orthogonal List)是有向图的另一种链式存储结构。该结构可以看成是将有向图的邻接表和逆邻接表结合起来得到的。用十字链表来存储有向图，可以达到高效的存取效果。

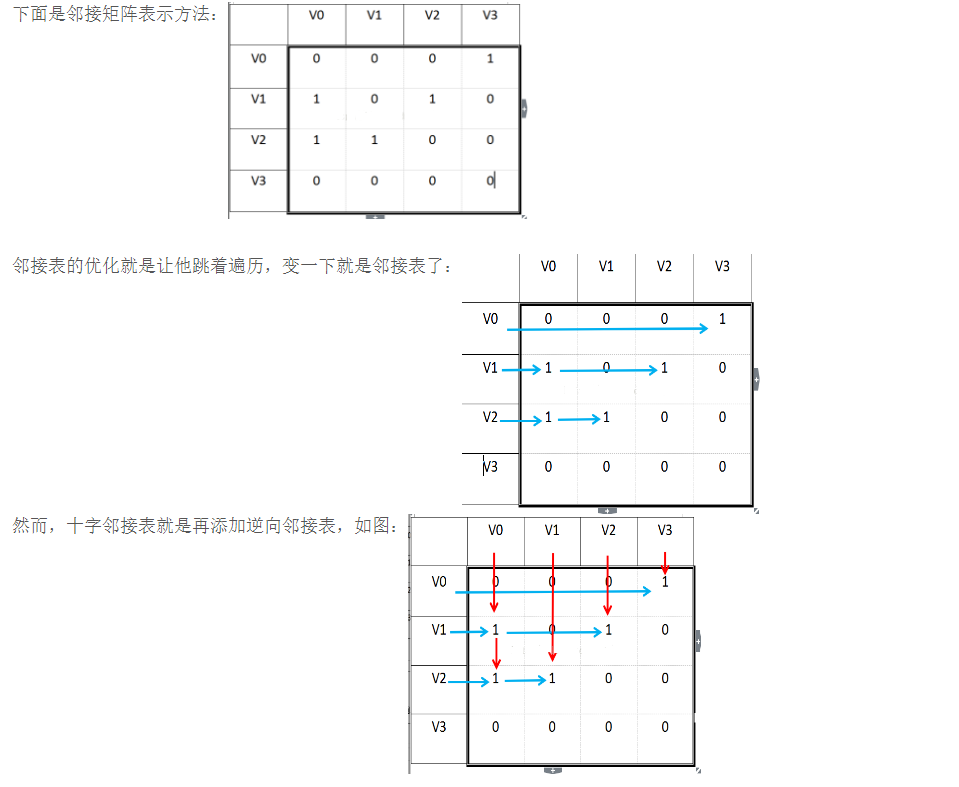
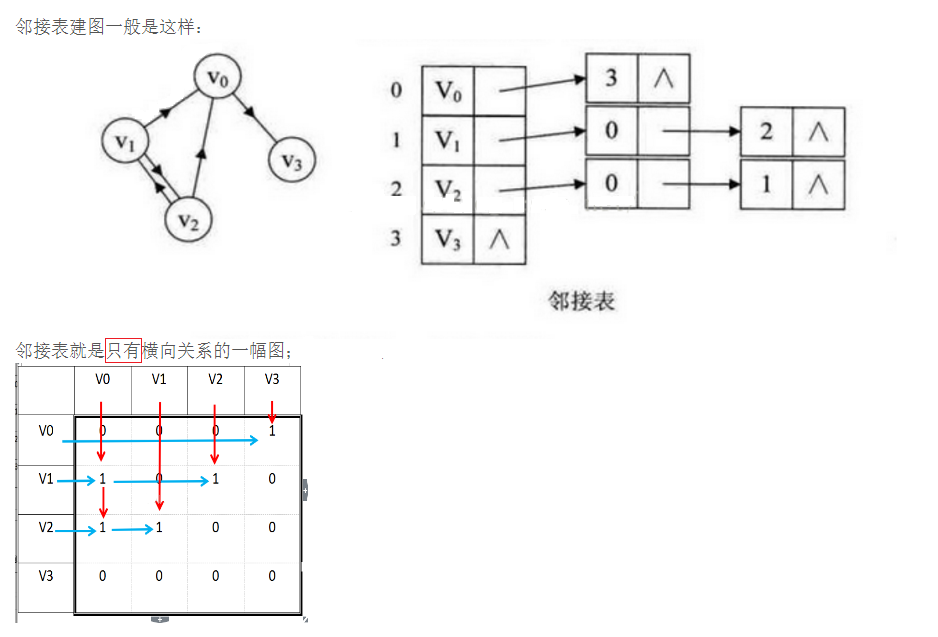
• 下面是邻接表和十字链表的关系
  
  

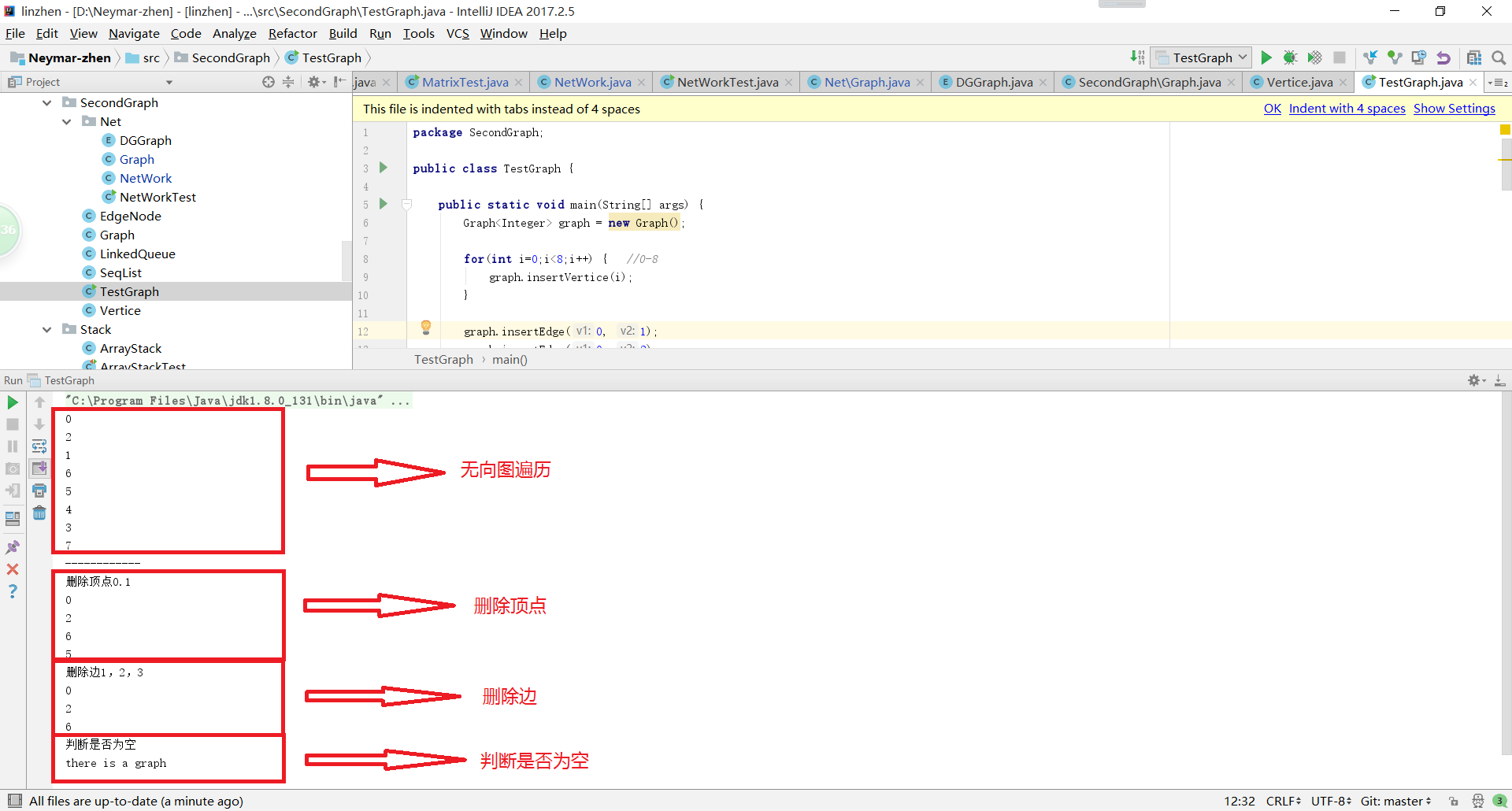
• 代码运行结果
  

项目三

项目分析

• pp19.9 的题目是：创建计算机网络路由系统，输入网络中点到点的线路，以及每条线路使用的费用，系统输出网络中各点之间最便宜的路径，指出不相通的所有位置

• 娄老师给的PPT给出了计算机网络中传输的问题讲解

• 本项目的核心在于求得顶点到任意点的最短路径，提供的常用算法有戴克斯特拉，及Dijikstra算法。该算法中需要引入一个辅助向量D，它的每个分量D[i]存放当前所找到的从源点到各个终点的最短路径长度。

• Dijkstra算法求最短路径的过程：

• 1. 令 S={v}，其中v为源点，并设定D[i]的初始值为
     D[i] = |v,vi|
• 2. 选择顶点vj使得
     D[j] = min

• 并将顶点vj并入到集合S中。

• 3. 对集合V-S中所有顶点vk，若D[j]+|vj,vk| < D[k],则修改D[k]的值为
     D[k]=D[j]+|vj,vk|

• 4)重复操作2)3)共n-1次，由此求得从源点到所有其他顶点的最短路径
  

• 代码运行结果