Leetcode刷题指南
1. 数据结构
1.1 数组
- 循环数组问题:把数组扩大为两倍即可,但不是真的扩大两倍,而是通过索引取模的方式
1.2 链表
链表可以通过引入虚拟头节点 ListNode *dummy = new ListNode{-1, nullptr} 来极大简化
-
递归:要区分基础情况和跳出情况,即可以有两种 return,比如:如果链表为空,那么返回。这时候的 return 并非是用来跳出递归的,而是一个 base 情况的判断,只有最基本的(最后一层递归)会用到。一系列操作,比如反转链表之后,再 return,则时候是退出递归的 return,即后面每一层递归想出栈都是走的这一条 return。
-
反转链表【递归】:反转从
head->next开始的链表,然后拼接上第一个节点。base:单节点链表 -
反转前 n 个元素:反转从
head->next开始的n-1个元素,然后拼接。base:n = 1 -
反转 [m, n] 的元素:反转从
head->next开始的[m-1, n - 1]的元素,然后拼接。base:m = 1,同上 -
倒序输出链表:对链表进行后序遍历,(递归的 base 是,head==nil)
1.3 栈与队列
单调队列
有这样一类问题:如何得到一个队列中的最值?遍历,然后维护一个最值就好了。但这会有一个问题:当最值出队之后,次最值无从得知,需要再次遍历。可以参考例题:
【剑指 Offer:队列最大值】,【leetcode-1438. 绝对差不超过限制的最长连续子数组(解法二)】
如何快速得到一个队列中,当前所有元素的最值呢?维护一个单调队列 queueMax,对入队元素 Value,如果 queueMax.back() > value,则直接入队,否则一直 queueMax.pop_back(),直至满足该条件。这样便可以保证:对原队列中所有元素,单调队列的队首,总是其最大值。如果原队列出队,使得最值出队,则单调队列中的下一个,仍是原队列中剩余元素的最值。
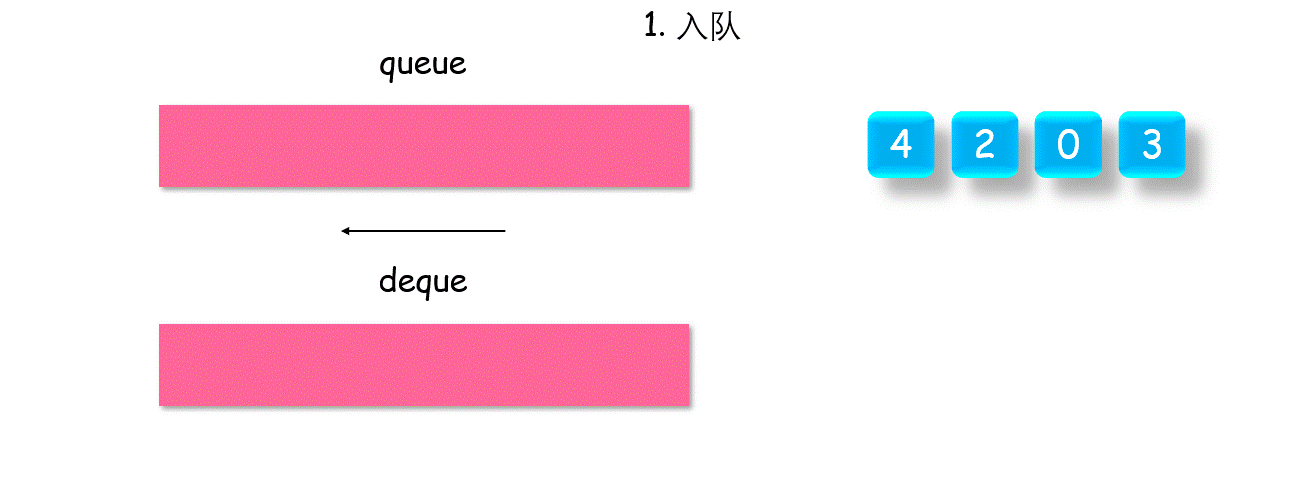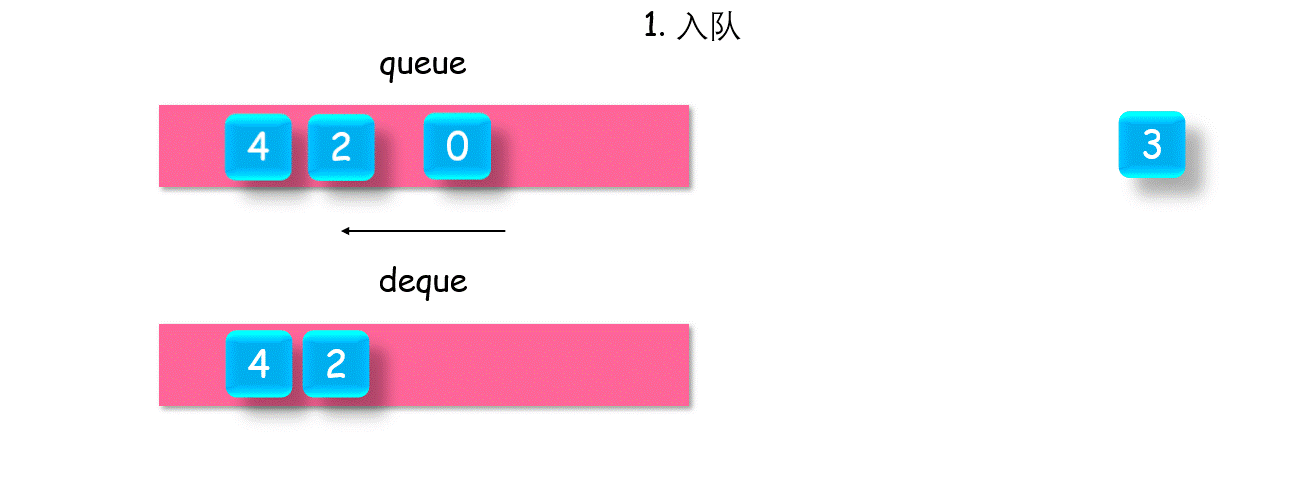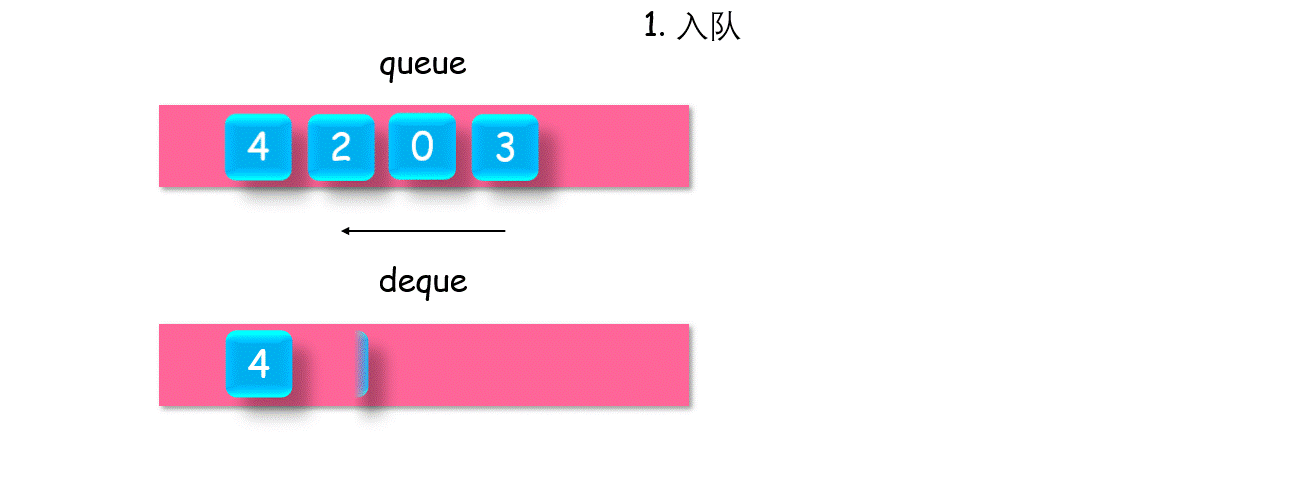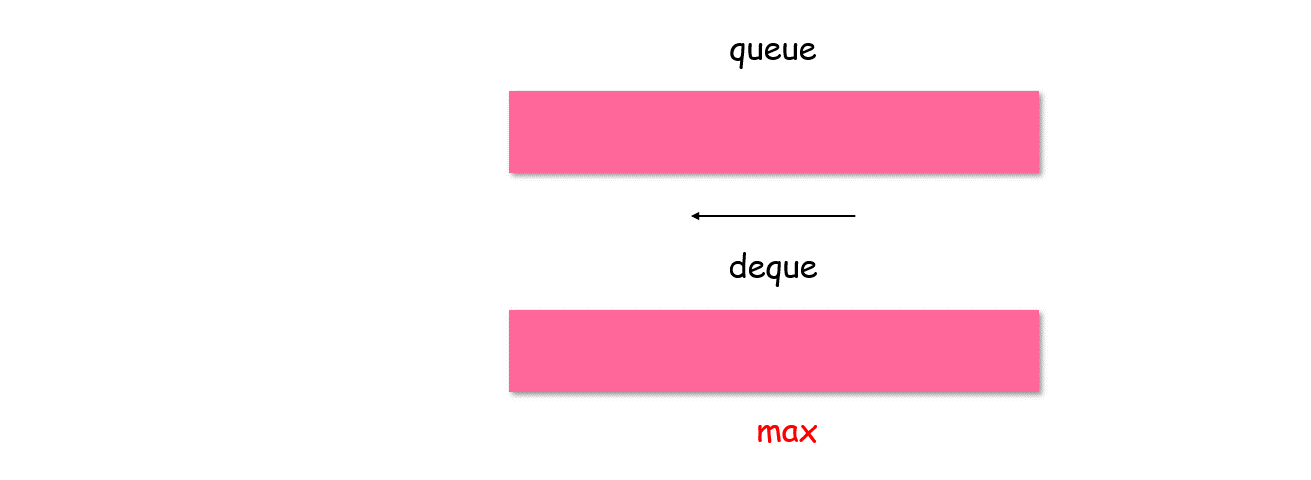
单调栈
类似的还有单调栈的问题 503. 下一个更大元素 II - 力扣(LeetCode):给你一个数组,有什么办法返回一个数组 res,使得 res 中存放原数组元素,其后面第一个比自己大的元素。也即利用单调栈寻找第一个大于自己的元素:
(1)数组从后往前入栈(出栈时即是顺序),如果栈顶元素小于自己,则一直出栈,直至栈顶大于自己,此时即有 ,再把当前元素入栈。
(2)从前入栈也可以(看题解写法)。从栈里的元素的角度看:元素先入栈,如果后面碰到比它大的元素,那它就会出栈;从要入栈的元素角度看,如果我比栈顶大,那就出栈,直到栈顶比我大我再入栈。这样一来,出栈就意味着,碰到了后面第一个比自己大的元素,而留在栈里的说明目前还没有比它大的。
下面是示意图:
而我们仍需一个数组来记忆元素的下一个大哥,所以如果直接是元素入栈的话,你只是知道了 2 的下一个大哥是 5,但是找不到 2 的索引,就没办法设置结果 stack2.pop();数组。因此可以采取:索引入栈、pair 入栈、哈希数组
索引入栈的话,即 ,如果大于栈顶,那就一直出栈(出的是索引),并且把出栈元素的邻近大哥(即 ret)标记为待入栈元素
2. 双指针
双指针一般用于数组字串和链表,尤其是二者还有序的情况。有三种双指针:
- 两指针:字面意义上的双指针,就是说有两个表需要遍历,你整俩指针出来
- 左右指针:左右分为,从两端往中间同时跑,和从中间往两边(最长回文子串)
- 快慢指针:又分为,同时出发一快一满,和速度相同,但其中一个先走(维持 k 间距)
- 滑动窗口:[left, right) 这么个区间,不断扩大 right,直至这是一个满足要求的窗口,然后缩小 left,使得此窗口为一个紧确的窗口,然后再扩大 right 搜索新的窗口,满足了再紧确,直至抵达边界。
注意滑动窗口,要分清何为"valid window",有时候这是一个大小不固定的,有时候又是固定大小的。
下面是一些应用:
(1)链表
- 求链表中点:二倍速指针走到末尾,一倍速走到中点
- 求链表倒数第 k 个节点:先走 k 步的离开末尾时,后面那个距离它为 k,即倒数第 k 个
- 判断链表有无环:地球是圆的的话,快慢指针终有相遇的一天
- 求出环的入口:快慢指针相遇之时,让一个重回起点再走,再次相遇即是在入口(列一下式子就出来了)
- 求两链表的交点:
① 两个指针各自遍历链表。在走到链表结尾的时候(p==nullptr),进入另一个链表。这样它们会走过相同的路程,即,该处即为交点。如果不相交,则走过 后会有: p==q==nullptr,也是相等
② 把其中一个链表的尾巴和另一个的头相连,就成了判断有无环,有就找到环入口的问题
③ 先求出两表的长度,让长的指针先走(long - short)步,这样链表就对齐了,对齐了就好办了
(2)数组
- 数组原地删除相同元素:(有序数组)快指针在前面探路,遇到不同的赋值给 slow++,这样前面的都不同
- 数组原地删除某一值:快指针在前面探路,只要不碰到 target,就赋值给 slow++
- 数组二分查找:(有序)最常见的双指针 low 和 high,或者叫 left 和 right
- 两数之和:(有序)两端开始,和大了就把大的缩点,和小了就把小的加点
- 原地反转数组:从两头开始互相交换【原地反转链表呢?>> 递归】
- 回文串判断:两头开始比较是否相等
- 求最大回文子串:从某一点或两点开始,往两边扩散求最长回文串;如此对全部元素都扩一遍,求最大值
盛水最多容器 11
题目:
如下图,给你一个数组 height,找出能“盛水”的最大值
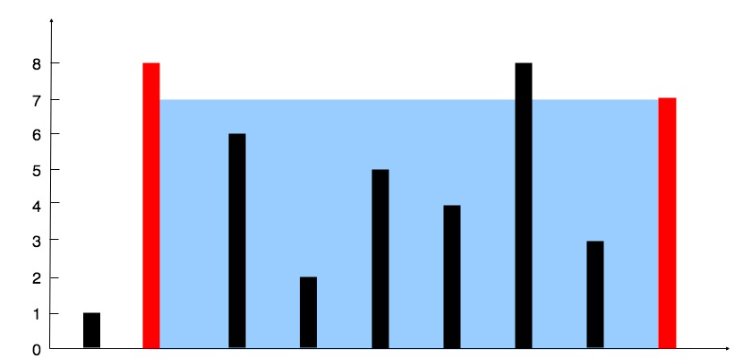
分析:
从两端扫一遍数组,则盛水量为:
现在考虑怎么个扫描法。反正只要移动,容器的“底”必然会变小,如果移动长板,那么容器的边最多不会超过原来的短板,因为边去的是最小值,移动后小于原来的短板,则变小,移动后大于,边也不会变大,因此移动长板,必然会使容量减小。那么就移动短边。
题解:
int maxArea(vector<int>& height) {
int l = 0, r = height.size() - 1;
int max_contain = 0;
while (l < r) {
int area = min(height[l], height[r]) * (r - l);
ans = max(max_contain, area);
if (height[l] <= height[r])
++l;
else
--r;
}
return max_contain;
}
3 二分法
对有序数组进行二分查找,有三种情况:只查找目标、查找目标元素序列左边界、右边界。
二分查找思想很简单,关键在一些细节:比如 right 是等于 size 还是 size-1, while 循环 还是 ,找着目标之后 right 是等于 mid 还是 mid-1。其实很好理解,只需要分清你的搜索区间是什么:
如果 ,那搜索区间就是闭区间 ,while 循环如果写,则退出条件就是,此时闭区间 里面还有一个元素,有元素还退出,那肯定是要漏了,所以应该选,如果搜索区间为左闭右开则同理。
搜索目标的左右边界,与直接搜索目标区别在于:找到目标后不是直接返回,而是继续缩小区间。搜元素是命中时退出,搜边界一定是 left > right 退出。那么:
- 如果存在目标元素,则到最后一定是 ,只需
return nums[left]; - 如果目标不存在,则
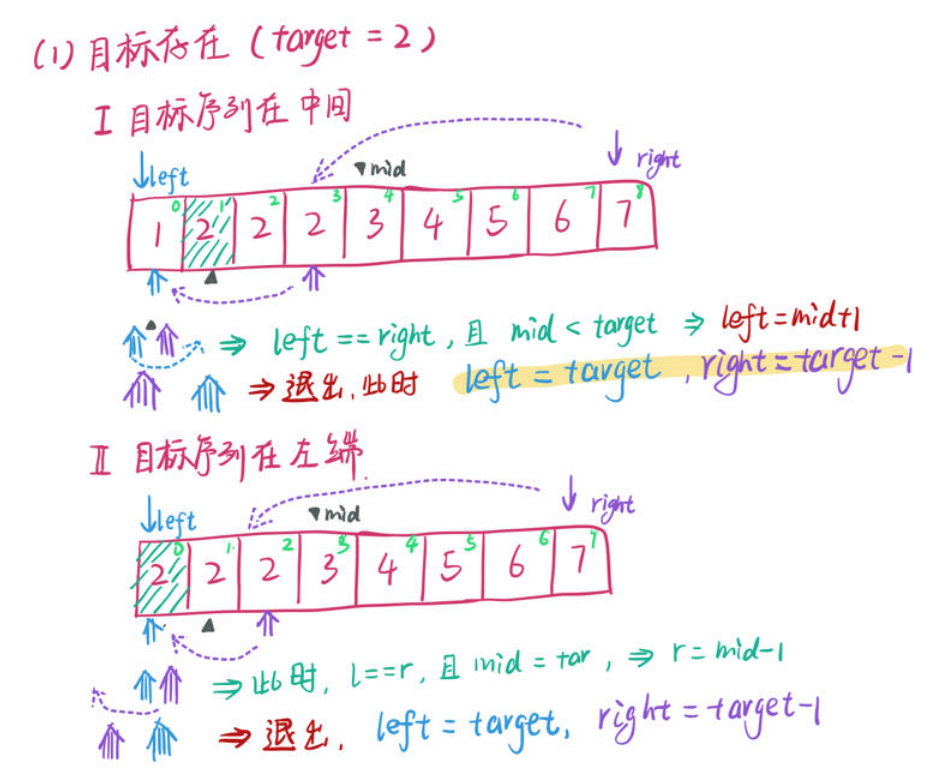 |
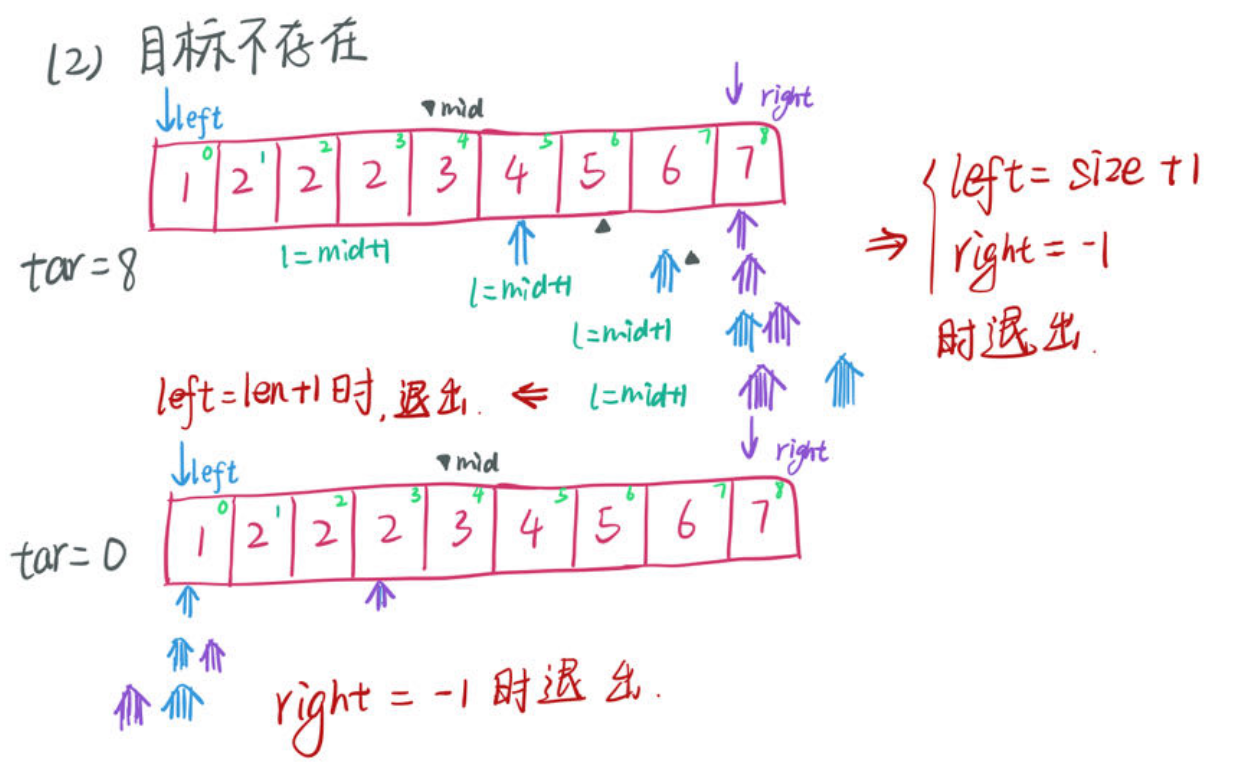 |
模板如下
int left_bound(int nums[], int target) {
int left = 0, right = nums.length - 1; //(0)
while (left <= right) { //(1)
// 防止加法溢出
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 别返回,锁定左侧边界
right = mid - 1; //(2)
}
}
// 判断 target 是否存在于 nums 中
// 此时 target ⽐所有数都大/小,返回 -1
if (left == nums.length || right == -1) //(3)
return -1;
return left;
}
下面是一些应用:
- 查找峰值:【无序】也可以二分,即先比较 mid 和两边的元素大小,如果 mid 在上坡,则说明峰值在前方,left = mid + 1,如果在下坡,说明在后方,right = mid - 1,如果直接命中,则返回
4 贪心 & 动态规划
4.1 线性 DP
1 斐波那契数列
矩阵快速幂
其实斐波那契数列还有一个O(log n) 复杂度的做法:用矩阵快速幂,转换成求这么个矩阵的 n 次幂
而矩阵快速幂,跟一般的快速幂都是类似的,都是将幂分解为二进制表示,,然后运用累乘的思想。
typedef vector<vector<double>> Matrix;
Matrix MatrixMultiply(const Matrix& A, const Matrix& B); // 自行实现矩阵相乘
Matrix MatrixPower(const Matrix& A, const int n){
// A^13 = A^8 * A^4 * A^1
int size = A.size();
// 创建一个结果矩阵,先初始化为 单位矩阵
Matrix result(size, vector<int>(size, 0));
for (int i = 0; i < size; i++) {
result[i][i] = 1;
}
Matrix base = A;
while (n > 0) {
// 如果该位上为 1,说明有 2^i 这一项,则乘上
if (n & 1) {
result = multiply(result, base);
}
// 将base自乘,用于下一位的计算
base = MatrixMultiply(base, base);
// 右移一位
n >>= 1;
}
return result;
}
O(log n) 的时间复杂度就是在base = MatrixMultiply(base, base); 这一步来的。因为将矩阵的幂换成了如干个 个幂相乘,最高不会超过 次,而且每个更高级的幂都是用低级的平方上去的,不会有额外复杂度
2 BST 种类
求由 n 个节点构成的 二叉搜索树 有多少种?
🤔两种方向:
动态规划应当有两种思考方向:
(1)从 1 到 n(自下而上):
一个节点:有一种;
两个节点:有两种,以小的为根,和以大的为根
三个节点:有三种情况:最小的作为根,中间的作为根,最大的作为根。
更多节点:同上了,俺顺序,依次选取不同的根,元素就会被分成两部分。
可得递推式:
这里用到了乘法原理。这里的 0,要说空树也是树嘛,为了公式的整齐性,也应将其置为 1
(2)从 n 到 1(自上而下):
n 个节点的树,肯定是要分为左右子树的,则自然有:。而左右子树具体有多少个节点,那肯定也不一样嘛,因此:
殊途同归。具体问题的时候,可以往下想想,往上想想,就能把问题拆解清楚了。线性 DP,还是比较简单的
3 最大子数组和
连续最大 和
给你一个数组有正有负,求连续的子数组,使得其和最大
把握核心:核心是什么?求最大子数组,核心当然是子数组。你只有分析子数组,才能找到最大的子数组
子数组怎么分呢?要动态规划,你肯定得从 0 做起,而且还要朝着一个方向坚定不移前进(往前推进),不能一会前一会后(前后可以考虑滑动窗口)。所以,要找一个朝着某一方向的,变化的子数组。所以:
以当前元素结尾的子数组的最大值,是 dp[i]
线性的,能不能优化为原地的呢?可以看到,只用到了 dp[i-1],完全可以用一个变量保存起来就好了
连续最大 积
思考一下,积,跟和的区别,在哪里呢?
积,会存在负负得正的情况。因此,当前结尾的最大子数组积,
要么是前面的最大的正数,乘了一个大于 1 的正数,变大了;要么是前面最大的乘了一个正真分数,变小了;要么,是前面的负的最小值,乘了一个负数,变大了。
因此最大值有三种来历:正正,负负,当前元素
显然,也是可以优化为原地 dp 的
连续最大 乘积为正
乘积为正的子数组:要么负负得正,负数加一;要么正正,正的加一;要么归 0
环形数组 最大和
环形数组,都可以转换成数组二倍。是环形数组,则遍历一遍 就相当于遍历了环
因此照着这个遍历一遍就好了(不用真的扩充数组,到末尾的时候再回到开始就好了)。相当于得到了 dp 数组之后,又回过头来更新一遍
4 字符串
最长编辑距离
将一个字符串变成(增加、删除字符)另一个字符串,最少需要多少次操作?
用 表示字符串 和 的编辑的最少次数。则 都是可“预知”的。 然后,添加一个或两个元素
如图,共有一下三种对齐方式:最后一位补上,和最后一位不一样
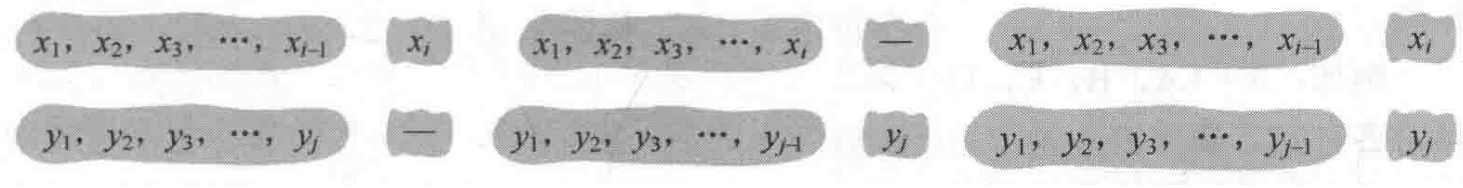
股票最佳时机
股票最佳时机 Ⅰ 121
题目:
给一个 prices 数组表示每天股票的价格,只能某天买入,后面一天卖出,求能赚的最大利润。
分析:
今天的最大利润,等于昨天的最大利润,与之前最低时买入并在今天卖出所得利润,的最大值。即
类比后面几种,也可以写成,
题解:
int maxProfit(vector<int>& prices) {
int inf = 1e9;
int minprice = inf, maxprofit = 0;
for (int price: prices) {
maxprofit = max(maxprofit, price - minprice);
minprice = min(price, minprice);
}
return maxprofit;
}
股票最佳时机 Ⅱ 122
题目:
仍然是 prices 数组表示每日价格,区别是,可以进行多次买卖,但是每一天手里最多只能有一只股票。即买了就得卖,不卖不能再买。求最大利润。
与 Ⅰ 的区别在于,能多次买卖,只不过必须是一买一卖,不能同时持有多支。
分析:
由于最多持有一只股票,因此第 i 天只有两种情况:持有一支和 0 支,分别用和表示。每天的最大利润等于,要么卖了更赚,要么前一天就最赚。则有状态转移方程如下:
初值,也即第一天时,,最后卖了肯定比不卖赚,因此最大值即为。
同样的,类比一下,这里也可以不用二维数组。
题解:
int maxProfit(vector<int>& prices) {
int dp0 = 0, dp1 = -prices[0];
int len = prices.size();
for(int i = 1; i < len; i++) {
// 这里可以直接操作dp0即可
dp0 = max(dp0, dp1 + prices[i]);
dp1 = max(dp1, dp0 - prices[i]);
// int new_dp0 = max(dp0, dp1 + prices[i]);
// int new_dp1 = max(dp1, dp0 - prices[i]);
// dp0 = new_dp0;
// dp1 = new_dp1;
}
return dp0;
}
股票最佳时机 Ⅲ 123
题目:
还是 prices 数组,但是最多只能进行两次买卖,且最多同时持有一支股票。
与 Ⅱ 的区别在于,限制了交易次数,最多两次。
分析:
某一天,最多有五种操作:不买,买了一支,卖了一支,买了第二支,卖了第二支。对应的状态转移方程为:
加上'表示前一天的值。buy0,不买肯定是 0,不用考虑。最后最赚的,如果卖了两支那就两支最赚,返回 sell2,如果买了一支,那么,买了没卖一定比卖了赚的少。因此最后返回值为 sell2
另外,这里直接对
题解:
int maxProfit(vector<int>& prices) {
int buy1 = -prices[0], sell1 = 0;
int buy2 = -prices[0], sell2 = 0;
for(int i = 1; i < prices.size(); i++) {
buy1 = max(buy1, 0 - prices[i]);
sell1 = max(sell1, buy1 + prices[i]);
buy2 = max(buy2, sell1 - prices[i]);
sell2 = max(sell2, buy2 + prices[i]);
}
return sell2;
}
股票最佳时机 Ⅳ 188
题目:
还还还是那个 prices 数组,你可以进行k次交易,仍然是最多同时持有一支股票。
与 Ⅲ 的区别在于,从 2 次改成了 k 次
分析:
解法同上,区别在于,限制买两次,每天是 5 种状态,限制买 k 次,每天还是那么分析状态,用一个 for 循环表示出来即可。要注意初始化时,buy 要全部初始化为-p0,因为一天可以连续买卖。
题解:
int maxProfit(int k, vector<int>& prices) {
vector<int> buy(k+1, -prices[0]);
vector<int> sell(k+1, 0);
buy[0] = 0;
for(int i = 1; i < prices.size(); ++i) {
for(int j = 1; j <= k; ++j) {
buy[j] = max(buy[j], sell[j - 1] - prices[i]);
sell[j] = max(sell[j], buy[j] + prices[i]);
}
}
return sell[k];
}
停下思考 1
上面这几个股票问题,采用了动态规划方法解决。那么他们的最优子结构是什么呢?
可以举几个最优子结构的例子进行类比学习:
最佳游艇租赁,假设最优路径有中间停靠站 k,那左右两边的租赁价格都得是最小
矩阵链乘,假设要从中间 k 处分割,那么左右的链乘代价都得是最小的
最长公共子序列,假设Z 是 X 和 Y 的最长公共子序列,那么,如果三者末位元素相等,那么去掉一个,Zk-1还的是 Xm-1、Yn-1的最长子序列。如果末尾元素不同,那么去掉那个不同的(假设是 X 的末位),Zk还得是 Xm-1与 Yn的最长子序列
基因编辑(字符串变为另一字符串所需的最小代价),假设X 和 Y 的最短编辑距离是
d[i][j],那么对于 X 和 Y 的右侧,要么放得对齐:相同了不编辑,不同则编辑;要么不对齐:去掉长的,或给短的插入一个。反正均可以用 d 表示出来:
0-1 背包,
20230303:都是先假设最优解存在,将最优解设出来,然后去表示子问题的最优解(即递推)。我认为股票的最优子结构是,每一天买卖股票所能获得的最大利润。知道了前面每一天的,就能知道最后一天的答案。分析 dp 解题步骤:找状态转移方程分析初值,然后就可以写循环了


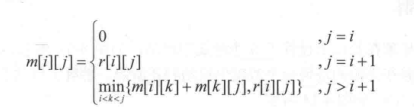
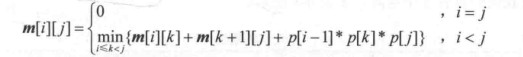
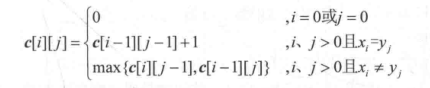
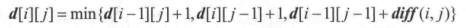


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 全程不用写代码,我用AI程序员写了一个飞机大战
· MongoDB 8.0这个新功能碉堡了,比商业数据库还牛
· 记一次.NET内存居高不下排查解决与启示
· DeepSeek 开源周回顾「GitHub 热点速览」
· 白话解读 Dapr 1.15:你的「微服务管家」又秀新绝活了