ACM-ICPC 2018 南京赛区网络预赛 B. The writing on the wall (暴力）

题意:一个n*m的方格矩阵,有的格子被涂成了黑色,问该矩阵中有多少个子矩阵,子矩阵不包含黑色格子;

思路:对于一个长为L, 高为H的无黑点矩阵中包含的高为H的子矩阵个数为L+(L-1)+(L-2)+...+1个；这是直接算的一种方法；如何程序表示该计算呢？

for(int i=1; i<=L; i++){
    for(int j=i; j>0; j--){
        count+=1;
    }
}

这样的一个双层循环就表示了上式；那么所有子矩阵个数就是三层循环，高由1->H：

for(int h=1; h<=H; h++){
    for(int i=1; i<=L; i++){
        for(int j=i; j>0; j--){
            count+=h;
        }
    }
}
 
​

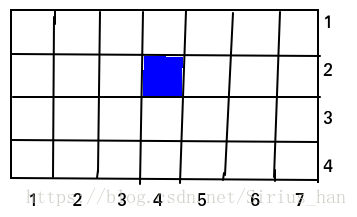
这是其中没有黑点的；如果在某处加了个黑点又如何计算呢？如下图：

先看高为H(4)的子矩阵个数：以(4, 7)为右下角的高为H的子矩阵个数为3个，由L=4处在向左，就只能构成高为2的子矩阵了；

那么怎么该上边的代码才能得出答案呢？如下：

for(int i=1; i<=H; i++){
    for(int j=1; j<=L; j++){
        h=i;
        for(int k=j; k>0; k--){
            h=min(h, i-p[k]);
            count+=h;
        }
    }
}
//p[k]表示第k列中在i行上边的第一个黑点的位置，

上边代码就是本题的核心代码了；然后H用n代替，L用m代替，这样复杂度为O(n*m*m)；然后标记黑点的位置每次维护h就可以了

#include<stdio.h>
#include<algorithm>
using namespace std;
int  a[100001][101],b[101];
int main( )
{
    int t , cas = 0;

    scanf("%d",&t) ;

    while(t--)
    {
        cas++;
        int n , m , id ;
        scanf("%d%d%d",&n,&m,&id);
        for(int i=0 ; i<=n ; i++)
        for(int j=0 ; j<=m ; j++)
        {
            a[i][j]=0;
            b[j]=0;
        }
        for(int i=0 ; i<id ; i++)
        {
            int x,y;
            scanf("%d%d",&x,&y);
            a[x][y]=1;
        }
        long long ans = 0 ;
        for(int i=1 ; i<=n ; i++)
        {
            for(int j=1 ; j<=m ; j++)
            {
                if(a[i][j])
                b[j]=i;
            }

            for(int j=1 ; j<=m ; j++)
            {
                int MINX = 0x3f3f3f3f ;
                for(int k=j ; k>0 ; k--)
                {
                    MINX = min(MINX,(i-b[k]));
                    ans+=MINX;
                }
            }
        }
        printf("Case #%d: %lld\n",cas , ans);

    }
}

感谢