codeforces C. Vasya And The Mushrooms (思维+模拟）

题意：给定一个2*n的矩形方格，每个格子有一个权值，从（0,0）开始出发，要求遍历完整个网格（不能重复走一个格子），求最大权值和，（权值和是按照step*w累加，step步数从0开始）。

转载：

题解:思维题,如果正向考虑的话很容易把自己绕晕,我们需要反过来想,你会发现其实对于一个2*N的矩阵,你一共只有N个终点(如下图1),如果在认真推敲,你会发现对于这n个终点,从起点到终点的路线都是很有规律的,只有下图2和3两种情况)那么问题就简单了,只需要考虑各种前缀的预处理,之后直接O(n)判断这N个终点得到的最大贡献即可~

图一

图二

图三

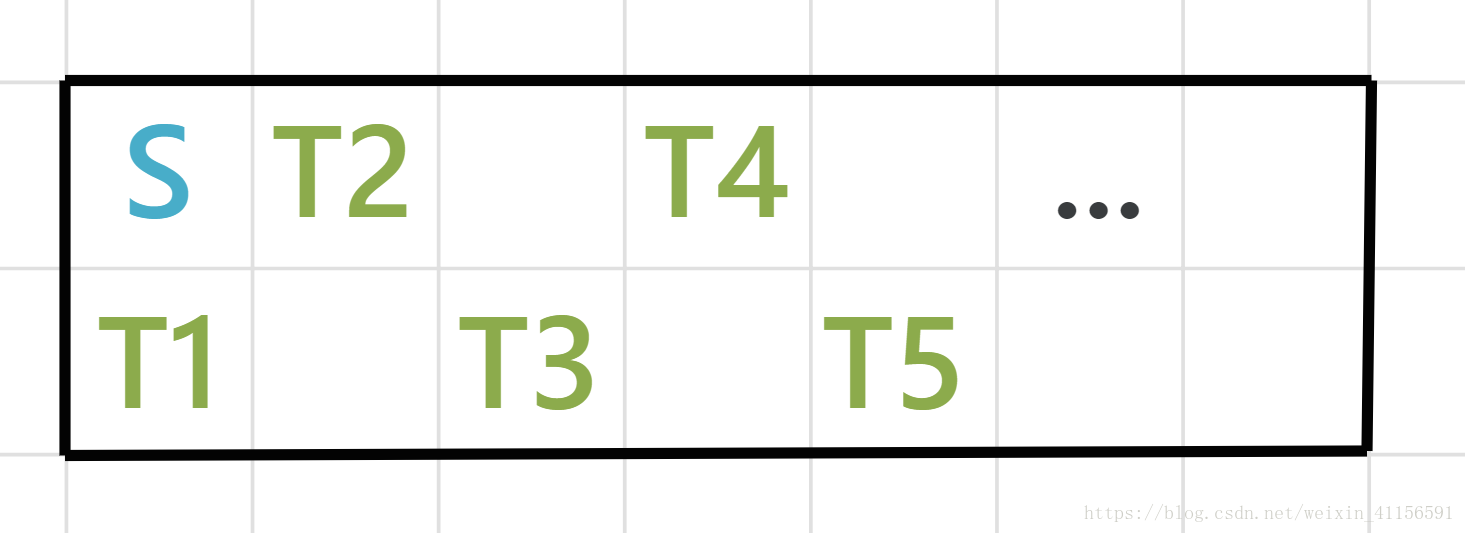
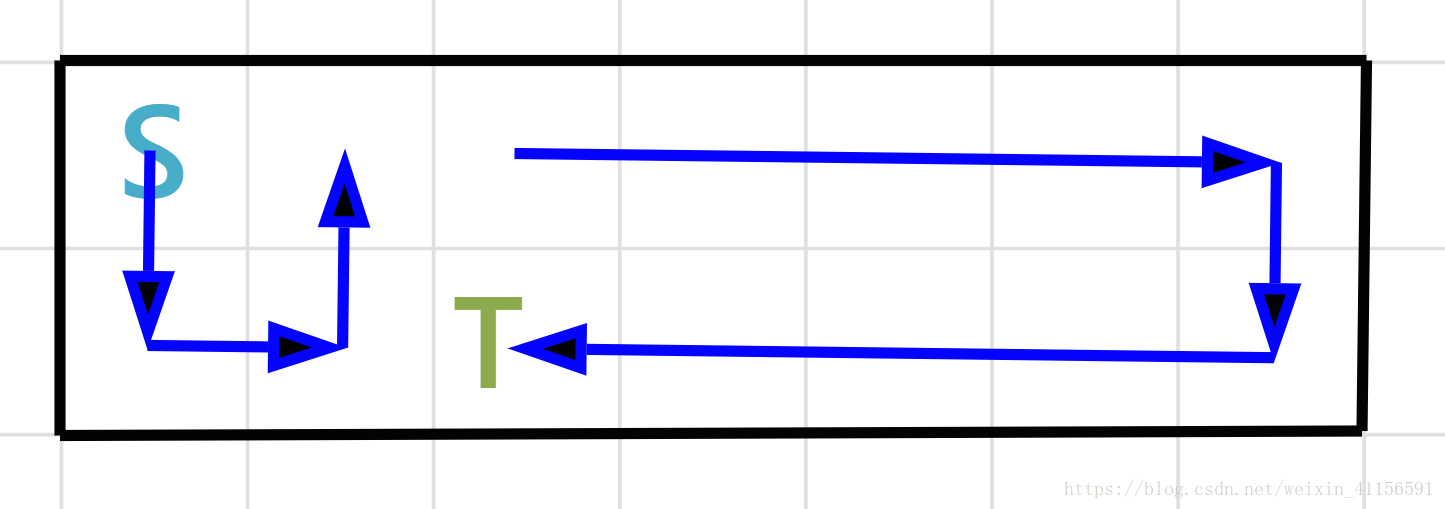
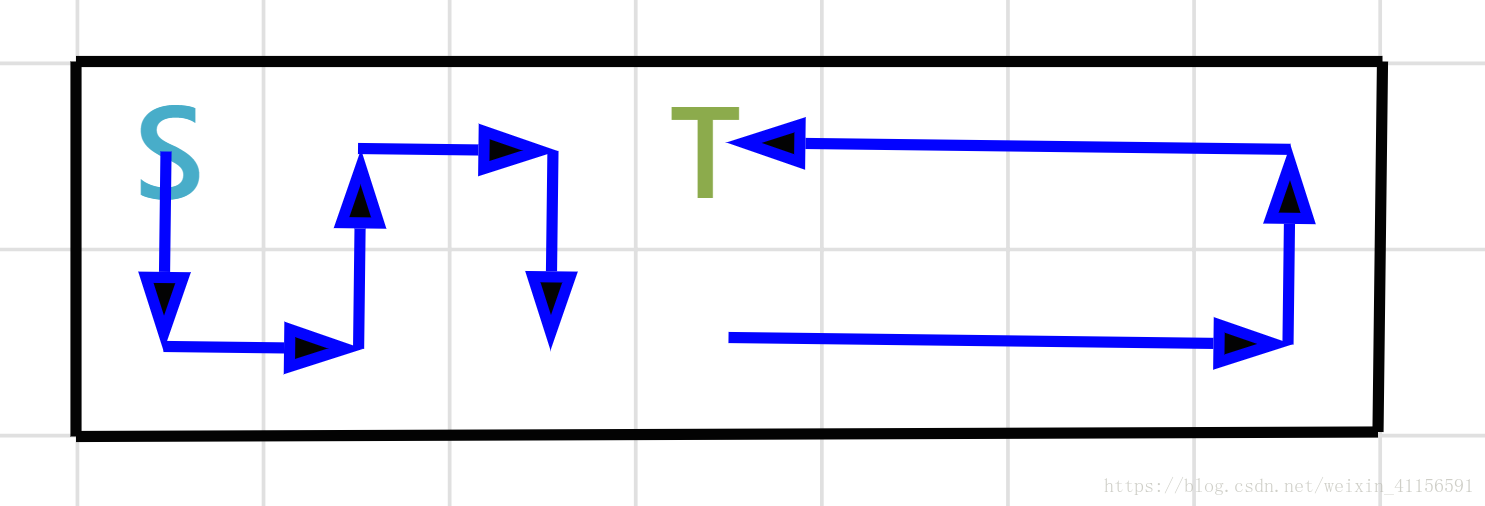
可以发现需要得到的是每个终点左边的贡献和右边的贡献,左边的贡献都是蛇形的,只用处理一个数组保存,右边由于有顺时针和逆时针,所有需要处理2个数组维护前缀和等~

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include <vector>
#include<queue>
#include <stack>
#include <map>
#define maxn 605005
#define INF 0x3f3f3f3f
#define LL long long
using namespace std;
LL n;
LL a[maxn];
LL b[maxn];
LL sum_s[maxn];//顺时针的从1~2n的前缀和
LL sum_n[maxn];//逆时针的从1~2n的前缀和
LL sumpre[maxn];//取i~n列的a[i]+b[i]和
LL suml[maxn];//对于一种路线中的左边部分
LL sumr[maxn];//同理，右边部分
LL ans;
void init( )
{
    for(int i=n ; i>=1 ; i--)
    sumpre[i]=sumpre[i+1]+a[i]+b[i];
    for(int i=1 ; i<=n ; i++)
    {
        sum_s[i]=sum_s[i-1]+(i-1)*a[i];
        sum_n[i]=sum_n[i-1]+(i-1)*b[i];
    }
    for(int i=n ; i>=1 ; i--)
    {
        sum_s[2*n-i+1]=sum_s[2*n-i]+(2*n-i)*b[i];
        sum_n[2*n-i+1]=sum_n[2*n-i]+(2*n-i)*a[i];
    }
    for(int i=1 ; i<=n ; i++)
    {
        if(i%2==1)
        {
            suml[i] = suml[i-1] + (2*i-3)*a[i-1] + (2*i-4)*b[i-1];
            sumr[i] = sum_s[2*n-i+1]-sum_s[i-1]+(i-1)*sumpre[i];
        }
        else
        {
            suml[i]=suml[i-1]+(2*i-4)*a[i-1]+(2*i-3)*b[i-1];
            sumr[i]=sum_n[2*n-i+1]-sum_n[i-1]+(i-1)*sumpre[i];
        }

    }
}
int main( )
{
    scanf("%d",&n);
    for(int i=1 ; i<=n ; i++)
    scanf("%d",&a[i]);
    for(int i=1 ; i<=n ; i++)
    scanf("%d",&b[i]);
    init();
    ans=0;
    for(int i=1 ; i<=n ; i++)
    {
        ans=max(ans,suml[i]+sumr[i]);
    }
    printf("%I64d\n",ans);
    return 0;
}

 

给自己的一点忠告，分析问题不能太过的片面，要打开思维走向未来