匈牙利算法
匈牙利算法是由匈牙利数学家Edmonds于1965年提出,因而得名。匈牙利算法是基于Hall定理中充分性证明的思想,它是部图匹配最常见的算法,该算法的核心就是寻找增广路径,它是一种用增广路径求二分图最大匹配的算法。
-------等等,看得头大?那么请看下面的版本:
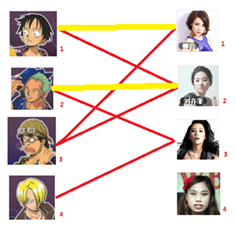
通过数代人的努力,你终于赶上了剩男剩女的大潮,假设你是一位光荣的新世纪媒人,在你的手上有N个剩男,M个剩女,每个人都可能对多名异性有好感( -_-||暂时不考虑特殊的性取向),如果一对男女互有好感,那么你就可以把这一对撮合在一起,现在让我们无视掉所有的单相思(好忧伤的感觉
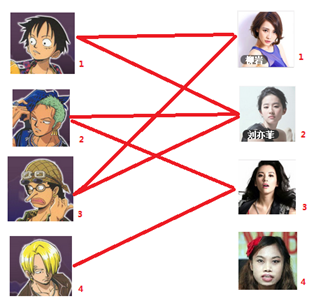
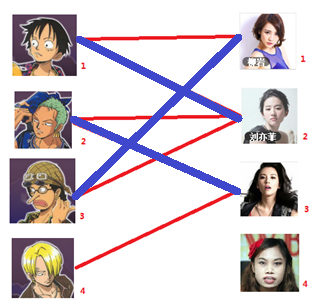
-_-||暂时不考虑特殊的性取向),如果一对男女互有好感,那么你就可以把这一对撮合在一起,现在让我们无视掉所有的单相思(好忧伤的感觉 ),你拥有的大概就是下面这样一张关系图,每一条连线都表示互有好感。
),你拥有的大概就是下面这样一张关系图,每一条连线都表示互有好感。
本着救人一命,胜造七级浮屠的原则,你想要尽可能地撮合更多的情侣,匈牙利算法的工作模式会教你这样做:
===============================================================================
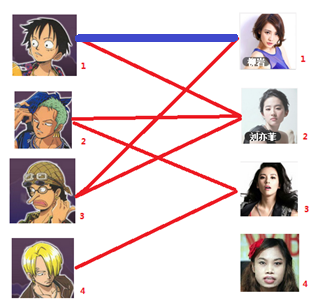
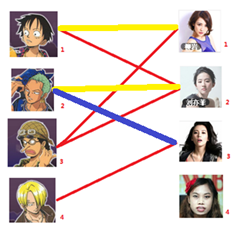
一: 先试着给1号男生找妹子,发现第一个和他相连的1号女生还名花无主,got it,连上一条蓝线
===============================================================================
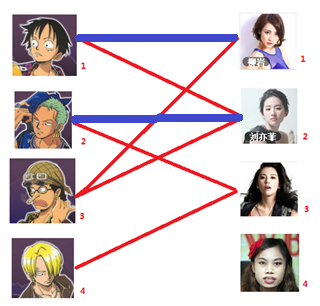
二:接着给2号男生找妹子,发现第一个和他相连的2号女生名花无主,got it
===============================================================================
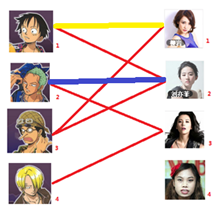
三:接下来是3号男生,很遗憾1号女生已经有主了,怎么办呢?
我们试着给之前1号女生匹配的男生(也就是1号男生)另外分配一个妹子。
(黄色表示这条边被临时拆掉)
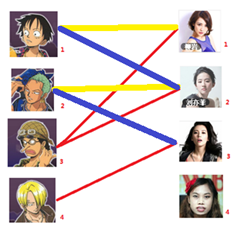
与1号男生相连的第二个女生是2号女生,但是2号女生也有主了,怎么办呢?我们再试着给2号女生的原配(
 )重新找个妹子(注意这个步骤和上面是一样的,这是一个递归的过程)
)重新找个妹子(注意这个步骤和上面是一样的,这是一个递归的过程)
此时发现2号男生还能找到3号女生,那么之前的问题迎刃而解了,回溯回去
2号男生可以找3号妹子~~~ 1号男生可以找2号妹子了~~~ 3号男生可以找1号妹子
所以第三步最后的结果就是:
===============================================================================
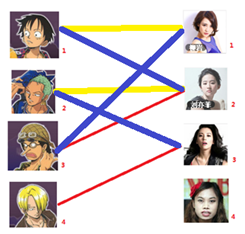
四: 接下来是4号男生,很遗憾,按照第三步的节奏我们没法给4号男生腾出来一个妹子,我们实在是无能为力了……香吉士同学走好。
===============================================================================
其原则大概是:有机会上,没机会创造机会也要上
bool find(int x){ int i,j; for (j=1;j<=m;j++){ //扫描每个妹子 if (line[x][j]==true && used[j]==false) //如果有暧昧并且还没有标记过(这里标记的意思是这次查找曾试图改变过该妹子的归属问题,但是没有成功,所以就不用瞎费工夫了) { used[j]=1; if (girl[j]==0 || find(girl[j])) { //名花无主或者能腾出个位置来,这里使用递归 girl[j]=x; return true; } } } return false; }
题意是说有n头cows和m个stalls。每头cows都有自己向往的stalls,但是每个stall只能容纳一头cow,每头cow也只能进一个stall。现在给你每头cow所向往的stall,让你求最多有多少头cows可以到自己向往的stall。

#include<stdio.h> #include<string.h> #define M 207 using namespace std; int g[M][M],link[M]; bool vis[M]; int n,m; bool find(int i) { for(int j=1 ; j<=n ; j++) if(g[i][j]&&!vis[j]) { vis[j]=true; if(link[j]==0||find(link[j])) { link[j]=i; return true; } } return false; } int main() { while(scanf("%d%d",&n,&m)!=EOF) { memset(link,0,sizeof(link)); memset(g,0,sizeof(g)); int num,a,count=0; for(int i=1 ; i<=n ; i++) { scanf("%d",&num); while(num--) { scanf("%d",&a); g[i][a]=1; } } for(int i=1 ; i<=n ; i++) { memset(vis,false,sizeof(vis)); if(find(i)) count++; } printf("%d\n",count); } return 0; }
POJ 1486 :
题意:
一些幻灯片,有一些数字在幻灯片里面,看能不能使得一个数字只能对应一张幻灯片.第一行代表有几张幻灯片.
给出这几张幻灯片的坐标,接着n行代表1-n个数字对应的坐标,然后要求你打印一个确定的使一个数字对应一张幻灯片.
如果不能对应输出none.
存在某些幻灯片只能由某个数字代表的话就按字典序打印出这些幻灯片和对应的数字.
分析:
这题很容易就可以想到用匈牙利算法,但是如何确定是必要点呢,这是个问题,我们可以尝试依此删除一条边然后在二分匹配,看看匹配数是否为N,如果还是那可以说明这是不必要的。
其实就是二分图最大匹配问题.左边点集用幻灯片编号表示,右边点集用数字表示. 如果某个幻灯片i包含了数字j,那么从左边i到右边j就存在一条边.
首先我们求出这个图的最大匹配数x, 根据题意这x值一定是等于n(幻灯片数的). 然后我们记录目前求到的最大匹配的各个边.
我们每次判断最大匹配边集的某条边是否是必需边. 我们只要先删除这条边,如果之后求最大匹配数依然==n,那么这条边不是必需边.如果之后求最大匹配数依然<n,那么这条边是必需边.(做好标记)
最终我们只需要输出所有的必须边即可.

#include<iostream> #include<cstdio> #include<cstring> #include<cstdlib> using namespace std; #define MAX 1000 int map[MAX][MAX],path[MAX]; int visit[MAX],result[MAX]; struct cam { int x1,x2,y1,y2; }list[MAX]; int n; int find(int a) { int i; for(i=0;i<n;i++) if(!visit[i]&&map[a][i]) { visit[i]=1; if(result[i]==-1||find(result[i])) { result[i]=a; return 1; } } return 0; } int solve() { int i,ans; ans=0; memset(result,-1,sizeof(result)); for(i=0;i<n;i++) { memset(visit,0,sizeof(visit)); if(find(i)) ans++; } return ans; } int main() { int x1,x2,y1,y2,i,j,flag; int x,y; int cas=1,ans; while(scanf("%d",&n),n) { for(i=0;i<n;i++) scanf("%d%d%d%d",&list[i].x1,&list[i].x2,&list[i].y1,&list[i].y2); memset(map,0,sizeof(map)); for(i=0;i<n;i++) { scanf("%d%d",&x,&y); for(j=0;j<n;j++) { if(x>list[j].x1&&x<list[j].x2&&y>list[j].y1&&y<list[j].y2) map[i][j]=1; } } ans=solve(); flag=0; printf("Heap %d\n", cas++); if(ans==n) { for(i=0;i<n;i++) path[i]=result[i]; for(i=0;i<n;i++) { map[path[i]][i]=0; //删边 if(solve()==n) //再做一次二分匹配 continue; else { /*if(flag) printf(" ");*/ printf("(%c,%d) ",'A'+i,path[i]+1); flag=1; } map[path[i]][i]=1; } } if(!flag) printf("none"); printf("\n\n"); } return 0; }
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
一道使用静态邻接表的代码:

#include<cstdio> #include<cstring> const int MAXN=500+10; int res[MAXN],head[MAXN],len; bool vis[MAXN]; struct edge { int to,next; }e[MAXN*MAXN]; void add(int from,int to) { e[len].to=to; e[len].next=head[from]; head[from]=len++; } bool find(int a) { for(int i=head[a];i!=-1;i=e[i].next) { int id=e[i].to; if(!vis[id]) { vis[id]=true; if(res[id]==0 || find(res[id]) ) { res[id]=a; return true; } } } return false; } int main() { int n; while(~scanf("%d",&n)) { memset(res,0,sizeof(res)); memset(head,-1,sizeof(head)); len=0; for(int i=0;i<n;i++) { int x,cnt; scanf("%d: (%d)",&x,&cnt); for(int j=0;j<cnt;j++) { int to; scanf("%d",&to); add(x,to); } } int ans=0; for(int i=0;i<n;i++) { memset(vis,0,sizeof(vis)); if(find(i)) ans++; } printf("%d\n",n-ans/2); } }