tarjan算法,一个关于 图的联通性的神奇算法
一.算法简介
Tarjan 算法一种由Robert Tarjan提出的求解有向图强连通分量的算法,它能做到线性时间的复杂度。
我们定义:
如果两个顶点可以相互通达,则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通,称G是一个强连通图。有向图的极大强连通子图,称为强连通分量(strongly connected components)。
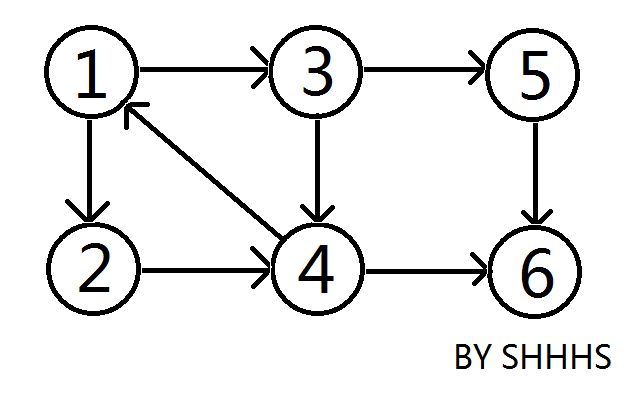
例如:在上图中,{1 , 2 , 3 , 4 } , { 5 } , { 6 } 三个区域可以相互连通,称为这个图的强连通分量。
Tarjan算法是基于对图深度优先搜索的算法,每个强连通分量为搜索树中的一棵子树。搜索时,把当前搜索树中未处理的节点加入一个堆栈,回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。
再Tarjan算法中,有如下定义。
DFN[ i ] : 在DFS中该节点被搜索的次序(时间戳)
LOW[ i ] : 为i或i的子树能够追溯到的最早的栈中节点的次序号
当DFN[ i ]==LOW[ i ]时,为i或i的子树可以构成一个强连通分量。
二.算法图示
以1为Tarjan 算法的起始点,如图
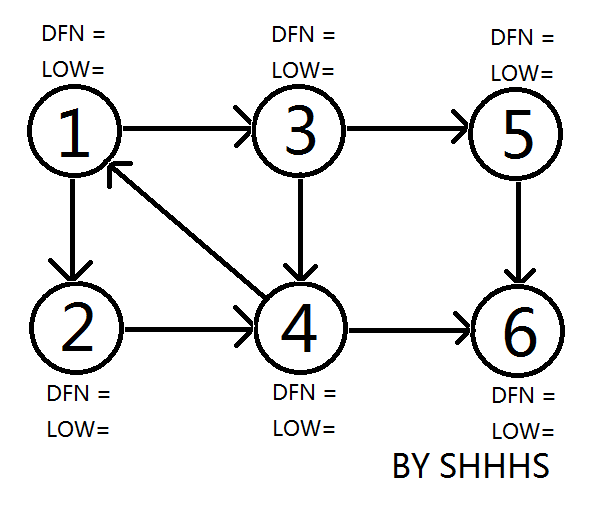
顺次DFS搜到节点6
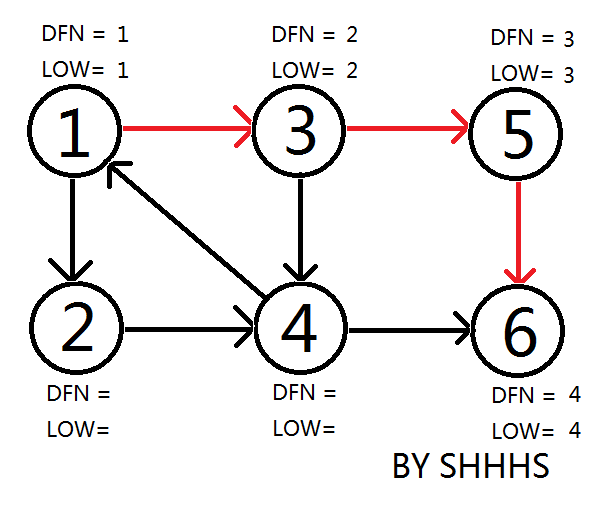
回溯时发现LOW[ 5 ]==DFN[ 5 ] , LOW[ 6 ]==DFN[ 6 ] ,则{ 5 } , { 6 } 为两个强连通分量。回溯至3节点,拓展节点4.
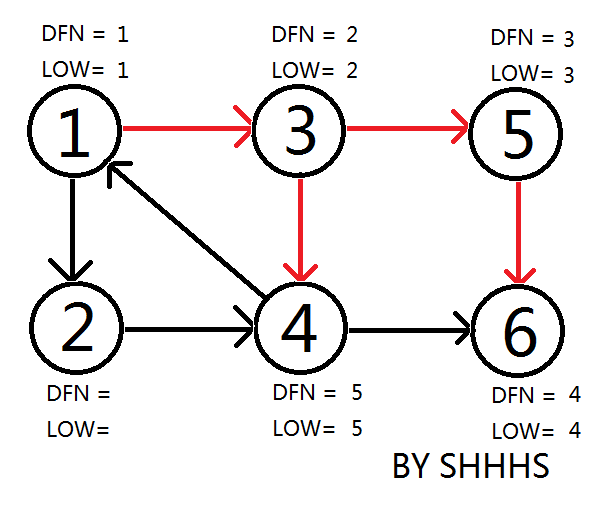
拓展节点1 , 发现1再栈中更新LOW[ 4 ],LOW[ 3 ] 的值为1
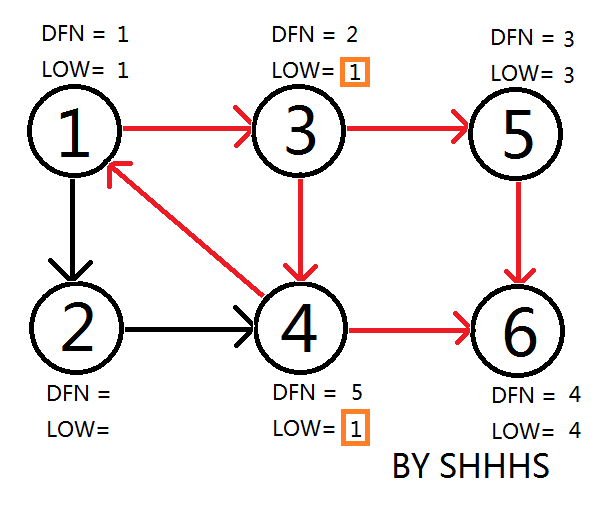
回溯节点1,拓展节点2
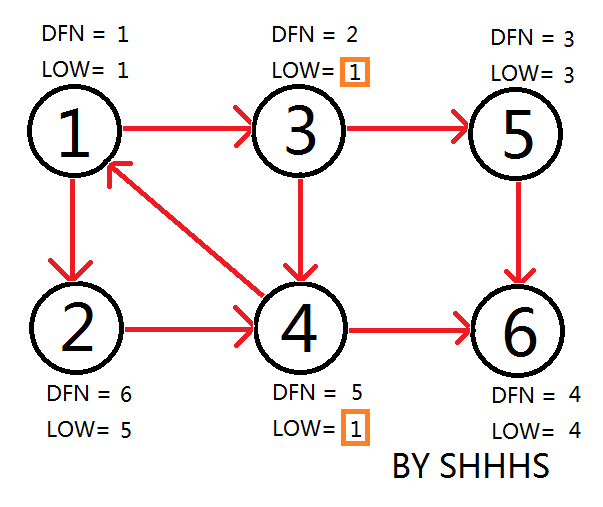
自此,Tarjan Algorithm 结束,{1 , 2 , 3 , 4 } , { 5 } , { 6 } 为图中的三个强连通分量。
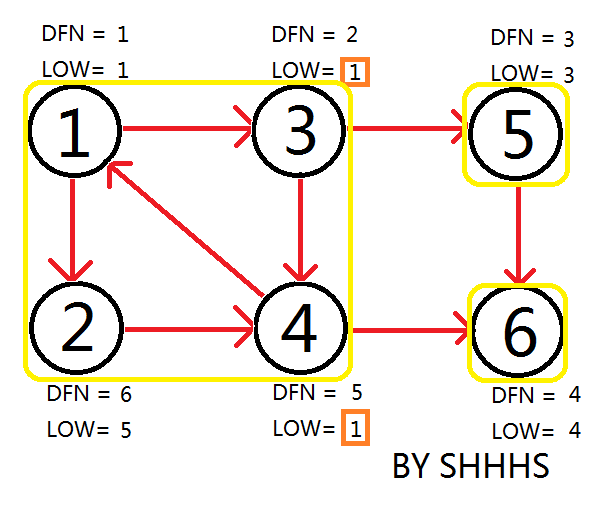
不难发现,Tarjan Algorithm 的时间复杂度为O(E+V).
模板:

1 void dfs(int u) 2 { 3 times++;//记录dfn顺序 4 dfn[u]=times;//赋值 5 low[u]=times;//先赋初值 6 vis[u]=true;//vis[i]用来判断i是否搜索过; 7 insta[u]=true;//表示是否在栈中,true为在栈中; 8 stack[top]=u;//栈顶 9 top++; 10 for(int i=head[u];i!=-1;i=edge[i].next)// 以建图顺序枚举此点所连的边 11 { 12 int v=edge[i].to;//搜索到的点 13 if(!vis[v])//如果未搜索过即未入栈 14 { 15 dfs(v);//继续以此点进行深搜 16 low[u]=min(low[u],low[v]);//更新low值,此边为树枝边所以比较u此时的 17 } // low值(未更新时就是其dfn值)和v的low值 18 else 19 if(insta[v]==true)//如果搜索过且在栈中,说明此边为后向边或栈中横叉边 20 { 21 low[u]=min(low[u],dfn[v]);//更新low值,比较u此时的low值和v的dfn值 22 } 23 } 24 25 if(low[u]==dfn[u])//相等说明找到一个强连通分量 26 { 27 while(top>0&&stack[top]!=u)//开始退栈一直退到 u为止 28 { 29 top--; 30 insta[stack[top]]=false; 31 } 32 } 33 }
例题:
poj2186 - Popular Cows
题目大意:题目大意是:在一个牧群中,有N个奶牛,给定M对关系(A,B)表示A仰慕B,而且仰慕关系有传递性,问被所有奶牛(除了自己)仰慕的奶牛个数
解题思路:找出所有的连通分量,如果只有一个连通分量的出度为0,那么输出那个连通分量的点的个数即可,如果不唯一就输出0
因为连通分量的出度有两个的话,那么肯定至少存在一头牛不仰慕另外一头牛,所以我们至少保证要出度为0的连通分量唯一
解题思路:
1、用Tarjan求双连通分量然后缩成点。这些点会形成一棵树。
2、求树上的节点有多少个出度为零,如果有一个就输出那个点里包含的所有点(因为是缩点出来的树)。
注意:
1、给出的图会有不连通的可能,如果那样肯定输出零。因为不连通肯定不会有所有其他牛认为某只牛很牛的情况出现。
2、如果缩点后有多个出度为零的点,那么输出零。因为这样图虽然联通了,但是还是不会出现所有其他牛认为某只牛很牛的情况(自己画一下就知道啦)。
求强连通分量主要是为了简化图的构造,如果分量外的一个点能到达分量内的其中一个点,那么它必定能到达分量内的所有点,所以某种程度上,强连通分量可以简化成一个点。

#include <stdio.h> #include <string.h> const int MAXN = 10005; const int MAXM = 100005; struct node { int to,next; } edge[MAXM]; int n,m,head[MAXN],dfn[MAXN],low[MAXN],stack1[MAXN],num[MAXN],du[MAXN],vis[MAXN],cnt,time,top,cut; void init() { memset(dfn,0,sizeof(dfn)); memset(low,0,sizeof(low)); memset(head,-1,sizeof(head)); memset(vis,0,sizeof(vis)); memset(num,0,sizeof(num)); memset(du,0,sizeof(du)); cnt=0; time=1; top=0; cut=0; } void addedge(int u,int v) { edge[cnt].to=v; edge[cnt].next=head[u]; head[u]=cnt; cnt++; } int min(int a,int b) { if(a>b)a=b; return a; } void dfs(int u,int fa) { dfn[u]=time; low[u]=time; time++; vis[u]=1; stack1[top]=u; top++; for(int i=head[u]; i!=-1; i=edge[i].next) { int v=edge[i].to; if(!vis[v]) { dfs(v,u); low[u]=min(low[u],low[v]); } else if(vis[v]) { low[u]=min(low[u],dfn[v]); } } if(low[u]==dfn[u]) { cut++; while(top>0&&stack1[top]!=u) { top--; vis[stack1[top]]=2; num[stack1[top]]=cut; } } } int main() { int i,u,v; while(scanf("%d%d",&n,&m)!=EOF) { init(); for(i=0; i<m; i++) { scanf("%d%d",&u,&v); addedge(u,v); } for(int i=1; i<=n; i++) { if(!vis[i]) { dfs(i,0); } } for(i=1; i<=n; i++) { for(int j=head[i]; j!=-1; j=edge[j].next) { if(num[i]!=num[edge[j].to]) { du[num[i]]++; } } } int sum=0,x; for(i=1; i<=cut; i++) { if(!du[i]) { sum++; x=i; } } if(sum==1) { sum=0; for(i=1; i<=n; i++) { if(num[i]==x) { sum++; } } printf("%d\n",sum); } else { puts("0"); } } return 0; }






