网络流——最小割求最大权闭合子图

定义

有一个有向图，每一个点都有一个权值（可以为正或负或0），选择一个权值和最大的子图，使得每个点的后继都在子图里面，这个子图就叫最大权闭合子图。 
如下图：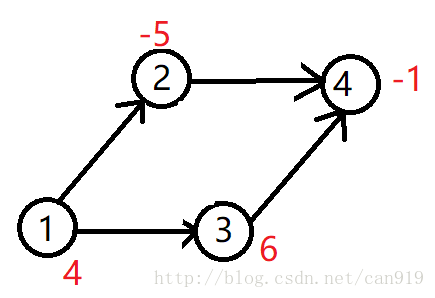 
 
能选的子图有Ø,{4},{3,4},{2,4},{1,2,3,4},它们的权值分别为0,-1,5,-6,4. 
所以最大权闭合子图为{3,4}，权值为5.

解法

这个问题可以转化为最小割问题，用网络流解决。 
从源点s向每个正权点连一条容量为权值的边，每个负权点向汇点t连一条容量为权值的绝对值的边，有向图原来的边容量全部为无限大。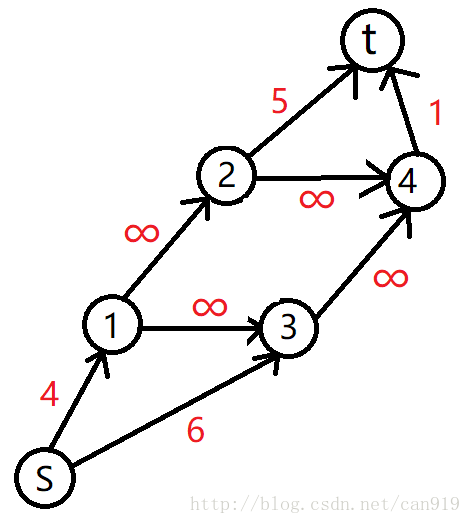 
 
求它的最小割，割掉后，与源点s连通的点构成最大权闭合子图，权值为（正权值之和-最小割）。

如何理解

割掉一条边的含义

由于原图的边都是无穷大，那么割边一定是与源点s或汇点t相连的。

割掉s与i的边，表示不选择i点作为子图的点； 
割掉i与t的边，表示选择i点为子图的点。

如果s与i有边，表示i存在子图中； 
如果i与t有边，表示i不存在于子图中。

合法性

只有s与t不连通时，才能得到闭合子图。

如果s与t连通，则存在点i,j，使得s到i有边，i到j连通，j到t有边，所以j一定是i的后继，但选择了i，没有选择j，不是闭合子图。

如果s与t不连通，选择了正权点i，一定选择了i后继中的所有负权点。设j是i的后继中的正权点，则割掉s到j的边是没有意义的，最小割不会割掉它，则j一点被选中，所以i的所有后继都被选中，符合闭合图的定义。

最优性

最小割=(不选的正权之和+要选的负权绝对值之和） 
最大权闭合子图=（正权之和-不选的正权之和-要选的负权绝对值之和）=正权值和-最小割 
因为正权值和，是定值，而最小割保证值最小，所以最大权闭合子图一定最优。

例题

POJ2987_Firing

AC代码

#include <iostream>
#include <vector>
#include <queue>
using namespace std;
 
typedef long long LL;
#define MAX_V 5000 + 16
 
// 用于表示边的结构体（终点、容量、反向边）
struct edge
{
    int to, rev;
    LL cap;
    edge(int to, LL cap, int rev) :to(to), cap(cap), rev(rev){}
};
 
vector<edge> G[MAX_V];    // 图的邻接表表示
int level[MAX_V];        // 顶点到源点的距离标号
int iter[MAX_V];        // 当前弧，在其之前的边已经没有用了
 
// 向图中加入一条从from到to的容量为cap的边
void add_edge(int from, int to, int cap)
{
    G[from].push_back(edge(to, cap, G[to].size() ));
    G[to].push_back(edge(from, 0, G[from].size() - 1));
}
 
// 通过BFS计算从源点出发的距离标号
void bfs(int s)
{
    memset(level, -1, sizeof(level));
    queue<int> que;
    level[s] = 0;
    que.push(s);
    while (!que.empty())
    {
        int v = que.front(); que.pop();
        for (int i = 0; i < G[v].size(); ++i)
        {
            edge& e = G[v][i];
            if (e.cap > 0 && level[e.to] < 0)
            {
                level[e.to] = level[v] + 1;
                que.push(e.to);
            }
        }
    }
}
 
// 通过DFS寻找增广路
LL dfs(int v, int t, LL f)
{
    if (v == t)
    {
        return f;
    }
    for (int& i = iter[v]; i < G[v].size(); ++i)
    {
        edge& e = G[v][i];
        if (e.cap > 0 && level[v] < level[e.to])
        {
            LL d = dfs(e.to, t, min(f, e.cap));
            if (d > 0)
            {
                e.cap -= d;
                G[e.to][e.rev].cap += d;
                return d;
            }
        }
    }
 
    return 0;
}
 
// 求解从s到t的最大流
LL max_flow(int s, int t)
{
    LL flow = 0;
    for (;;)
    {
        bfs(s);
        if (level[t] < 0) 
        {
            return flow;
        }
        memset(iter, 0, sizeof(iter));
        LL f;
        while ((f = dfs(s, t, 0x3f3f3f3f3f3f3f3f)) > 0)
        {
            flow += f;
        }
    }
}
 
int vertex_count, visited[MAX_V];
// 遍历残余网络
void solve(int v)
{
    ++vertex_count;
    visited[v] = true;
    for (int i = 0; i < int(G[v].size()); ++i) 
    {
        const edge &e = G[v][i];
        if (e.cap > 0 && !visited[e.to]) 
        {
            solve(e.to);
        }
    }
}
///////////////////////////SubMain//////////////////////////////////
int main(int argc, char *argv[])
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
    freopen("out.txt", "w", stdout);
#endif
    int n, m, w;
    LL W = 0;
    scanf("%d%d", &n, &m);
    const int s = 0, t = n + 1;
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &w);
        if (w > 0)
        {
            W += w;
            add_edge(s, i, w);
        }
        if (w < 0)
        {
            add_edge(i, t, -w);
        }
    }
 
    int u, v;
    for (int i = 0; i < m; ++i)
    {
        scanf("%d%d", &u, &v);
        add_edge(u, v, 0x3f3f3f3f3f3f3f3f);
    }
 
    LL max_profit = W - max_flow(s, t);
    solve(s);
    printf("%d %I64d\n", --vertex_count, max_profit);
#ifndef ONLINE_JUDGE
    fclose(stdin);
    fclose(stdout);
    system("out.txt");
#endif
    return 0;
}