坐标离散化

问题： 
在w*h的格子上画了n条垂直或者水平的宽度为1的直线。求出这些直线将格子划分为了多少个区域？ 
限制条件： 
1<= w,h <= 1000000 
1<= n <= 500 
输入：首先输入w,h,n;然后输入对应的x1,x2,y1,y2.输出区域的个数。 
输入： 
10 10 5 
x1:1 1 4 9 10 
x2:6 10 4 9 10 
y1:4 8 1 1 6 
y2:4 8 10 5 10 
输出： 
6

分析： 
我们可以用一个数组表示所有的格子，然后将格子分为直线上的和不在直线上的，然后进行BFS搜索。但是由于w,h很大，没办法开那么大的数组。所以我们要利用坐标离散化得技巧。 
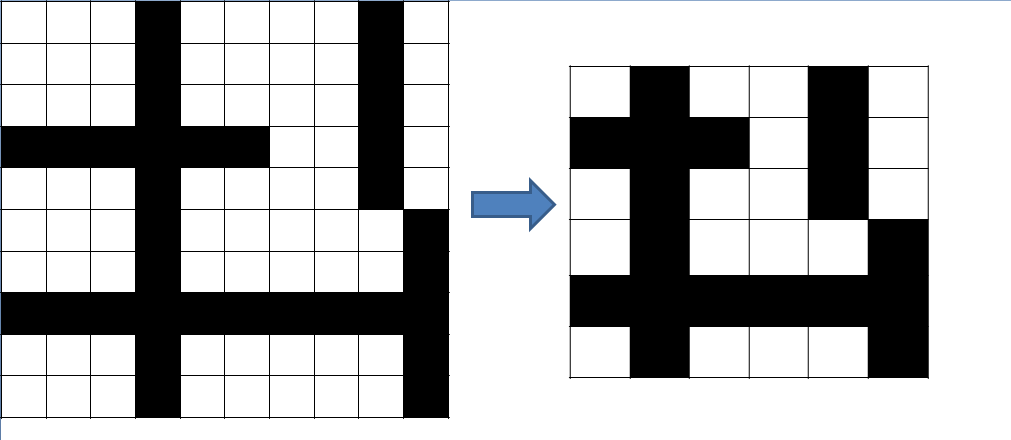
如输入样例所示： 

坐标离散化的主要思想是：将前后没有变化的行列消除后并不影响区域的个数 
数组里只需要存储有直线的行列和前后的行列就足够了，这样的话大小最多为6n*6n了。 
然后在利用BFS搜索即可。

现在我们来考虑个细节，如果我们原本是不相邻的，可我们离散化后就变的相邻了，怎么办？这样的话，我们就要做偏移处理，

下来的代码中for(int d=-1 ; d<=1 ; d++)  这个就是偏移处理，是为了防止这种情况的发生，为什么呢？

下面举个例子,5与8  如果没有偏移处理那5对应的是1，8对应的是2，那这两个是相邻的，但他们并不相邻，也就是x...x变成了xx，这是错误的，

那偏移后就是4,5,6,7,8,9; 5记录的是2，8记录的是5，那他们离散后表示的就没有相邻 

代码及其解析：

#include<bits/stdc++.h>
#define MAX 510
using namespace std;
int n,w,h;
int x1[MAX],x2[MAX],y2[MAX];
int Y1[MAX];
bool fld[MAX*6][MAX*6];
///对x1和x2进行坐标离散化，并返回离散化之后的宽度
///对x1,x2更新为离散后的x1,x2，y不变在x方向上缩小
int net[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
int compress( int *x1,int *x2,int w)
{
   vector<int> xs;
   ///确定离散后x轴上哪些值还有
   for(int i=0 ; i<n ; i++)
   {
       for(int d=-1 ; d<=1 ; d++)///偏移量，防止原本不相邻的离散后便相邻了；
       {
           int tx1=x1[i]+d,tx2=x2[i]+d;
           if(tx1>=1&&tx1<=w)
            xs.push_back(tx1);
           if(tx2>=1&&tx2<=w)
            xs.push_back(tx2);
       }
   }
   ///离散化两部曲
   sort(xs.begin(),xs.end());///排序
   xs.erase(unique(xs.begin(),xs.end()),xs.end());///去重
   ///转化为新的x1,x2
   for(int i=0 ; i<n ; i++)
   {
       x1[i]=find(xs.begin(),xs.end(),x1[i])-xs.begin();
       x2[i]=find(xs.begin(),xs.end(),x2[i])-xs.begin();
   }
   return xs.size( );
}
void so ( )
{
    ///坐标离散化
    w = compress(x1,x2,w);
    h = compress(Y1,y2,h);
    memset(fld,0,sizeof(fld));
    ///填充有直线的部分
    for(int i=0 ; i<n ; i++)
    {
        for(int y=Y1[i] ; y<=y2[i] ; y++)
        {
            for(int x=x1[i] ; x<=x2[i] ; x++)
                fld[y][x]=true;
        }
    }
    ///求区域的个数
    int ans=0;
    for(int y=0 ; y<h ; y++)
    {
        for(int x=0 ; x<w ; x++)
        {


            if(fld[y][x])
            continue;
        ans++;

    ///宽度优先搜索
    queue<pair<int,int> >que;
    que.push(make_pair(x,y));
    while(!que.empty())
    {
        int sx=que.front().first,sy=que.front().second;
        que.pop( );
        for(int i=0 ; i<4 ; i++)
        {
            int tx=sx+net[i][0],ty=sy+net[i][1];
            if(tx<0||ty<0||tx>=w||ty>=h)
            continue;
            if(fld[ty][tx])
            continue;
            que.push(make_pair(tx,ty));
            fld[ty][tx]=true;
        }
    }

    }
    }
    printf("%d\n",ans);

}
int main( )
{

   while( scanf("%d%d%d",&w,&h,&n)!=EOF)
   {
       for(int i=0 ; i<n ; i++)
        scanf("%d",&x1[i]);
       for(int i=0 ; i<n ; i++)
        scanf("%d",&x2[i]);
       for(int i=0 ; i<n ; i++)
        scanf("%d",&Y1[i]);
       for(int i=0 ; i<n ; i++)
        scanf("%d",&y2[i]);
       so( );
   }
}