对AC自动机+DP题的一些汇总与一丝总结 (2)
POJ 2778 DNA Sequence
(1)题意 : 给出m个病毒串,问你由ATGC构成的长度为 n 且不包含这些病毒串的个数有多少个
关键字眼:不包含,个数,长度
DP[i][j] : 表示长度为i,在trie图中j节点,不包含病毒串的个数
状态转移: DP[i+1][k]+=DP[i][j]*G[j][k] (G[j][k] 表示 在trie图的安全图中j 到 k是否有边)
但是!这题给出n长度特别大,故无法进行正常的DP; 我们在转换下思路
这题无非就是在全图中的0节点到其他节点刚好经过K步的方案数->(求从A点到B点刚好经过K步的方案数)
最后的结论就是将整幅图转化为邻接矩阵,然后对矩阵求 k 次幂,最后矩阵的(A, B)点数值就是答案

#include<queue> #include<stdio.h> #include<string.h> using namespace std; const int Max_Tot = 1e2 + 10; const int Letter = 4; const int MOD = 1e5; int maxn; int mp[128]; struct mat{ int m[111][111]; }unit, M; mat operator * (mat a, mat b) { mat ret; long long x; for(int i=0; i<maxn; i++){ for(int j=0; j<maxn; j++){ x = 0; for(int k=0; k<maxn; k++){ x += (long long)a.m[i][k]*b.m[k][j]; } ret.m[i][j] = x % MOD; } } return ret; } inline void init_unit() { for(int i=0; i<maxn; i++) unit.m[i][i] = 1; } mat pow_mat(mat a, int n) { mat ret = unit; while(n){ if(n&1) ret = ret * a; a = a*a; n >>= 1; } return ret; } struct Aho{ struct StateTable{ int Next[Letter]; int fail, flag; }Node[Max_Tot]; int Size; queue<int> que; inline void init(){ while(!que.empty()) que.pop(); memset(Node[0].Next, 0, sizeof(Node[0].Next)); Node[0].fail = Node[0].flag = 0; Size = 1; } inline void insert(char *s){ int now = 0; for(int i=0; s[i]; i++){ int idx = mp[s[i]]; if(!Node[now].Next[idx]){ memset(Node[Size].Next, 0, sizeof(Node[Size].Next)); Node[Size].fail = Node[Size].flag = 0; Node[now].Next[idx] = Size++; } now = Node[now].Next[idx]; } Node[now].flag = 1; } inline void BuildFail(){ Node[0].fail = 0; for(int i=0; i<Letter; i++){ if(Node[0].Next[i]){ Node[Node[0].Next[i]].fail = 0; que.push(Node[0].Next[i]); }else Node[0].Next[i] = 0;///必定指向根节点 } while(!que.empty()){ int top = que.front(); que.pop(); if(Node[Node[top].fail].flag) Node[top].flag = 1; for(int i=0; i<Letter; i++){ int &v = Node[top].Next[i]; if(v){ que.push(v); Node[v].fail = Node[Node[top].fail].Next[i]; }else v = Node[Node[top].fail].Next[i]; } } } inline void BuildMatrix(){ for(int i=0; i<Size; i++) for(int j=0; j<Size; j++) M.m[i][j] = 0; for(int i=0; i<Size; i++){ for(int j=0; j<Letter; j++){ if(!Node[i].flag && !Node[ Node[i].Next[j] ].flag) M.m[i][Node[i].Next[j]]++; } } maxn = Size; } }ac; char S[11]; int main(void) { mp['A']=0, mp['T']=1, mp['G']=2, mp['C']=3; int n, m; while(~scanf("%d %d", &m, &n)){ ac.init(); for(int i=0; i<m; i++){ scanf("%s", S); ac.insert(S); } ac.BuildFail(); ac.BuildMatrix(); init_unit(); M = pow_mat(M, n); int ans = 0; for(int i=0; i<ac.Size; i++) ans += M.m[0][i]; ans %= MOD; printf("%d\n", ans); } return 0; }
POJ 1625 Censored
(2)题意 : 给出 n 个单词组成的字符集 以及 p 个非法串,问你用字符集里面的单词构造长度为 m 的单词的方案数有多少种?
关键字眼:不包含(非法),个数,长度
定眼一看,不就是(1)的原题吗,啊对对对,那确实。
DP[i][j] : 表示长度为i,在trie图中j节点,不包含病毒串的个数
状态转移: DP[i+1][k]+=DP[i][j]*G[j][k] (G[j][k] 表示 在trie图的安全图中j 到 k是否有边)
这个还是不变的。 不过这题的长度不打,故不用矩阵快速幂,但是结果很多,需要高精度

#include<string.h> #include<stdio.h> #include<iostream> #include<queue> #include<map> using namespace std; const int Max_Tot = 111; const int Letter = 256; int G[111][111], n; map<int, int> mp; struct bign{ #define MAX_B (100) #define MOD (10000) int a[MAX_B], n; bign() { a[0] = 0, n = 1; } bign(int num) { n = 0; do { a[n++] = num % MOD; num /= MOD; } while(num); } bign& operator= (int num) { return *this = bign(num); } bign operator+ (const bign& b) const { bign c = bign(); int cn = max(n, b.n), d = 0; for(int i = 0, x, y; i < cn; i++) { x = (n > i) ? a[i] : 0; y = (b.n > i) ? b.a[i] : 0; c.a[i] = (x + y + d) % MOD; d = (x + y + d) / MOD; } if(d) c.a[cn++] = d; c.n = cn; return c; } bign& operator+= (const bign& b) { *this = *this + b; return *this; } bign operator* (const bign& b) const { bign c = bign(); int cn = n + b.n, d = 0; for(int i = 0; i <= cn; i++) c.a[i] = 0; for(int i = 0; i < n; i++) for(int j = 0; j < b.n; j++) { c.a[i + j] += a[i] * b.a[j]; c.a[i + j + 1] += c.a[i + j] / MOD; c.a[i + j] %= MOD; } while(cn > 0 && !c.a[cn-1]) cn--; if(!cn) cn++; c.n = cn; return c; } friend ostream& operator<< (ostream& _cout, const bign& num) { printf("%d", num.a[num.n - 1]); for(int i = num.n - 2; i >= 0; i--) printf("%04d", num.a[i]); return _cout; } }; struct Aho{ struct StateTable{ int Next[Letter]; int fail, flag; }Node[Max_Tot]; int Size; queue<int> que; inline void init(){ while(!que.empty()) que.pop(); memset(Node[0].Next, 0, sizeof(Node[0].Next)); Node[0].fail = Node[0].flag = 0; Size = 1; } inline void insert(char *s){ int now = 0; for(int i=0; s[i]; i++){ int idx = mp[s[i]]; if(!Node[now].Next[idx]){ memset(Node[Size].Next, 0, sizeof(Node[Size].Next)); Node[Size].fail = Node[Size].flag = 0; Node[now].Next[idx] = Size++; } now = Node[now].Next[idx]; } Node[now].flag = 1; } inline void BuildFail(){ Node[0].fail = 0; for(int i=0; i<n; i++){ if(Node[0].Next[i]){ Node[Node[0].Next[i]].fail = 0; que.push(Node[0].Next[i]); }else Node[0].Next[i] = 0;///必定指向根节点 } while(!que.empty()){ int top = que.front(); que.pop(); if(Node[Node[top].fail].flag) Node[top].flag = 1; for(int i=0; i<n; i++){ int &v = Node[top].Next[i]; if(v){ que.push(v); Node[v].fail = Node[Node[top].fail].Next[i]; }else v = Node[Node[top].fail].Next[i]; } } } inline void BuildMap(){ for(int i=0; i<Size; i++) for(int j=0; j<Size; j++) G[i][j] = 0; for(int i=0; i<Size; i++){ for(int j=0; j<n; j++){ if(!Node[ Node[i].Next[j] ].flag) G[i][Node[i].Next[j]]++; } } } }ac; #define MAX_M (55) bign dp[MAX_M][Max_Tot]; char s[51]; int main(void) { int m, p; while(~scanf("%d %d %d\n", &n, &m, &p)){ mp.clear(); gets(s); int len = strlen(s); for(int i=0; i<len; i++) mp[s[i]] = i; ac.init(); for(int i=0; i<p; i++){ gets(s); ac.insert(s); } ac.BuildFail(); ac.BuildMap(); for(int i=0; i<=m; i++) for(int j=0; j<ac.Size; j++) dp[i][j] = bign(); dp[0][0] = 1; for(int i=0; i<m; i++) for(int j=0; j<ac.Size; j++){ for(int k=0; k<ac.Size; k++){ dp[i+1][k] += dp[i][j] * G[j][k]; } } bign ans = bign(); for(int i=0; i<ac.Size; i++) ans += dp[m][i]; cout<<ans<<endl; } return 0; }
HDU 2243
(3)题意 : 长度不超过L,只由小写字母组成的,至少包含一个词根的单词,一共可能有多少个呢?这里就不考虑单词是否有实际意义。
关键字眼:至少包含一个,个数,长度不超过
对于至少包含一个词根的单词,浅显的想到求对立面(总方案-不包含一个词根) (因为都好算啊)
那问题就是变成:
长度为0 :all_0 - A^0
长度为1 : all_1 - A^1
............
长度为L : all_L - A^L
全部相加:(all_0+all_1+...all_L)-(A^0+A^1+..+A^L) -> (26^0+26^1+...+26^L) -(A^0+A^1+..+A^L)
幂和可以由矩阵快速幂来求:
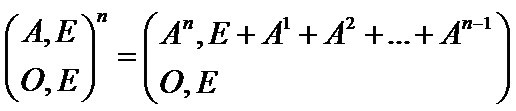

#include<string.h> #include<stdio.h> #include<iostream> #include<queue> #define ULL unsigned long long using namespace std; const int Max_Tot = 1e2 + 10; const int Letter = 26; int maxn;///矩阵的大小 char S[11]; struct mat{ ULL m[111][111]; }unit, M; mat operator * (mat a, mat b){ mat ret; for(int i=0; i<maxn; i++){ for(int j=0; j<maxn; j++){ ret.m[i][j] = (ULL)0; for(int k=0; k<maxn; k++){ ret.m[i][j] += a.m[i][k]*b.m[k][j]; } } } return ret; } inline void init_unit() { for(int i=0; i<maxn; i++) unit.m[i][i] = 1; } mat pow_mat(mat a, long long n){ mat ret = unit; while(n){ if(n&1) ret = ret * a; a = a*a; n >>= 1; } return ret; } struct Aho{ struct StateTable{ int Next[Letter]; int fail, flag; }Node[Max_Tot]; int Size; queue<int> que; inline void init(){ while(!que.empty()) que.pop(); memset(Node[0].Next, 0, sizeof(Node[0].Next)); Node[0].fail = Node[0].flag = 0; Size = 1; } inline void insert(char *s){ int now = 0; for(int i=0; s[i]; i++){ int idx = s[i] - 'a'; if(!Node[now].Next[idx]){ memset(Node[Size].Next, 0, sizeof(Node[Size].Next)); Node[Size].fail = Node[Size].flag = 0; Node[now].Next[idx] = Size++; } now = Node[now].Next[idx]; } Node[now].flag = 1; } inline void BuildFail(){ Node[0].fail = -1; for(int i=0; i<Letter; i++){ if(Node[0].Next[i]){ Node[Node[0].Next[i]].fail = 0; que.push(Node[0].Next[i]); }else Node[0].Next[i] = 0;///必定指向根节点 } while(!que.empty()){ int top = que.front(); que.pop(); if(Node[Node[top].fail].flag) Node[top].flag = 1; for(int i=0; i<Letter; i++){ int &v = Node[top].Next[i]; if(v){ que.push(v); Node[v].fail = Node[Node[top].fail].Next[i]; }else v = Node[Node[top].fail].Next[i]; } } } inline void BuildMatrix(){ for(int i=0; i<Size; i++) for(int j=0; j<Size; j++) M.m[i][j] = 0; for(int i=0; i<Size; i++){ for(int j=0; j<Letter; j++){ if(!Node[i].flag && !Node[ Node[i].Next[j] ].flag) M.m[i][Node[i].Next[j]]++; } } maxn = Size; } }ac; ULL GetSum(long long num){ mat ret; ret.m[0][0] = 26; ret.m[0][1] = 1; ret.m[1][0] = 0; ret.m[1][1] = 1; int tmp = maxn; maxn = 2; ret = pow_mat(ret, ++num); maxn = tmp; return ret.m[0][1]-1; } ULL GetElimination(long long num){ mat tmp; for(int i=0; i<maxn; i++)///左上角 为 原矩阵 for(int j=0; j<maxn; j++) tmp.m[i][j] = M.m[i][j]; for(int i=0; i<maxn; i++)///右上角 为 单位矩阵 for(int j=maxn; j<(maxn<<1); j++) tmp.m[i][j] = (i+maxn == j); for(int i=maxn; i<(maxn<<1); i++)///左下角 为 零矩阵 for(int j=0; j<maxn; j++) tmp.m[i][j] = 0; for(int i=maxn; i<(maxn<<1); i++)///右下角 为 单位矩阵 for(int j=maxn; j<(maxn<<1); j++) tmp.m[i][j] = (i==j); int Temp = maxn; maxn <<= 1;///先将原本矩阵的大小放大一倍进行快速幂运算,这个和我快速幂的写法有关 tmp = pow_mat(tmp, ++num); ULL ret = (ULL)0; maxn = Temp;///再回复成原来大小 for(int i=maxn; i<(maxn<<1); i++)///右上角的矩阵就是幂和了 ret += tmp.m[0][i]; return (--ret);///需要 -1 } int main(void) { int n, m; while(~scanf("%d %d", &m, &n)){ ac.init(); for(int i=0; i<m; i++){ scanf("%s", S); ac.insert(S); } ac.BuildFail(); ac.BuildMatrix(); init_unit(); ULL Tot = GetSum((long long)n);///注意是传long long不然会爆int ULL Elimination = GetElimination((long long)n); cout<<Tot-Elimination<<endl; } return 0; }
HDU 4511 小明系列故事——女友的考验 ( Trie图 && DP )
(4)题意 : 给出编号从1 ~ n 的 n 个平面直角坐标系上的点,求从给出的第一个点出发到达最后一个点的最短路径,其中有两种限制,其一就是只能从编号小的点到达编号大的点,再者不能走接下来给出的 m 个限制路径,也就是其中有些路线无法走。
把问题抽象一下就是用编号 1 ~ n 构造一个字符串,使得字符串不包含 m 个给出的子串,且构造的代价是最小的 ( 两点间距就是代价,也就是路长 )。 (这TM也可以转,NB)
关键词: 不包含
后定义 DP[i][j] = 在编号为 i 的点 且 在 Trie 图上编号为 j 的节点状态下,最短的路径长度是多少,则可得转移方程
DP[i+1][k] = min( DP[i+1][k], DP[i][j] + GetDis(i, k) ) 且 i+1 <= k <= n (保证编号从小到大)
其中 GetDis(i, k) 是坐标点 i 和 k 的距离、而且 Trie[j].Next[k].flag == 0 即在 Trie 图上 j 状态到 k 状态合法,并不会使其包含非法路径

#include<stdio.h> #include<string.h> #include<algorithm> #include<queue> #include<math.h> using namespace std; const int Max_Tot = 555; const int Letter = 55; const double INF = 1e20;///不能使用 0x3f3f3f3f int n, m; pair<int, int> Point[55]; struct Aho{ struct StateTable{ int Next[Letter]; int fail, flag; }Node[Max_Tot]; int Size; queue<int> que; inline void init(){ while(!que.empty()) que.pop(); memset(Node[0].Next, 0, sizeof(Node[0].Next)); Node[0].fail = Node[0].flag = 0; Size = 1; } inline void insert(int *s, int len){ int now = 0; for(int i=0; i<len; i++){ int idx = s[i]; if(!Node[now].Next[idx]){ memset(Node[Size].Next, 0, sizeof(Node[Size].Next)); Node[Size].fail = Node[Size].flag = 0; Node[now].Next[idx] = Size++; } now = Node[now].Next[idx]; } Node[now].flag = 1; } inline void BuildFail(){ Node[0].fail = 0; for(int i=0; i<n; i++){ if(Node[0].Next[i]){ Node[Node[0].Next[i]].fail = 0; que.push(Node[0].Next[i]); }else Node[0].Next[i] = 0;///必定指向根节点 } while(!que.empty()){ int top = que.front(); que.pop(); Node[top].flag |= Node[Node[top].fail].flag;///注意了!! for(int i=0; i<n; i++){ int &v = Node[top].Next[i]; if(v){ que.push(v); Node[v].fail = Node[Node[top].fail].Next[i]; }else v = Node[Node[top].fail].Next[i]; } } } }ac; double GetDis(pair<int,int> &st, pair<int,int> &en) { double x1 = (double)st.first; double x2 = (double)en.first; double y1 = (double)st.second; double y2 = (double)en.second; return sqrt( (double)(1.0*x1-x2)*(double)(1.0*x1-x2) + (double)(1.0*y1-y2)*(double)(1.0*y1-y2)); } double dp[55][555]; inline void Solve() { for(int i=0; i<n; i++) for(int j=0; j<ac.Size; j++) dp[i][j] = INF; dp[0][ac.Node[0].Next[0]] = 0; for(int i=0; i<n-1; i++){ for(int j=0; j<ac.Size; j++){ if(dp[i][j] < INF){ for(int k=i+1; k<n; k++){ int newi = k; int newj = ac.Node[j].Next[k]; if(!ac.Node[ newj ].flag){ dp[newi][newj] = min(dp[newi][newj], dp[i][j]+GetDis(Point[i], Point[k])); } } } } } double ans = INF; for(int i=0; i<ac.Size; i++) if(dp[n-1][i] < INF) ans = min(ans, dp[n-1][i]); if(ans == INF) puts("Can not be reached!"); else printf("%.2lf\n", ans); } int main(void) { while(~scanf("%d %d", &n, &m)){ if(n==0 && m==0) break; for(int i=0; i<n; i++)///这里我将编号 -1 了,也就是编号从 0 ~ n-1,所以下面操作都是按个编号来 scanf("%d %d", &Point[i].first, &Point[i].second); int tmp[10]; ac.init(); while(m--){ int k; scanf("%d", &k); for(int i=0; i<k; i++){ scanf("%d", &tmp[i]); tmp[i]--;///因为编号是 0 ~ n-1 } ac.insert(tmp, k); }ac.BuildFail(); Solve(); } return 0; }
POJ 3691 DNA repair ( Trie图 && DP )
题意 : 给出 n 个病毒串,最后再给出一个主串,问你最少改变主串中的多少个单词才能使得主串中不包含任何一个病毒串
关键词: 不包含,改变单词
if(Trie[k]不是被标记的病毒节点) DP[i+1][k] = min( DP[i+1][k], DP[i][j] + (mp[S[i]] != k) )
k 为 j 节点的四个下一状态,转到"ATGC"其中一个,而mp[]作用是把"ATGC"转为0、1、2、3
DP的初始状态为 DP[0][0] = 0,DP[0~len][0~节点数] = INF

#include<queue> #include<stdio.h> #include<string.h> using namespace std; const int Max_Tot = 1111; const int Letter = 4; const int INF = 0x3f3f3f3f; int mp[128]; struct Aho{ struct StateTable{ int Next[Letter]; int fail, flag; }Node[Max_Tot]; int Size; queue<int> que; inline void init(){ while(!que.empty()) que.pop(); memset(Node[0].Next, 0, sizeof(Node[0].Next)); Node[0].fail = Node[0].flag = 0; Size = 1; } inline void insert(char *s){ int now = 0; for(int i=0; s[i]; i++){ int idx = mp[s[i]]; if(!Node[now].Next[idx]){ memset(Node[Size].Next, 0, sizeof(Node[Size].Next)); Node[Size].fail = Node[Size].flag = 0; Node[now].Next[idx] = Size++; } now = Node[now].Next[idx]; } Node[now].flag = 1; } inline void BuildFail(){ Node[0].fail = 0; for(int i=0; i<Letter; i++){ if(Node[0].Next[i]){ Node[Node[0].Next[i]].fail = 0; que.push(Node[0].Next[i]); }else Node[0].Next[i] = 0;///必定指向根节点 } while(!que.empty()){ int top = que.front(); que.pop(); if(Node[Node[top].fail].flag) Node[top].flag = 1; for(int i=0; i<Letter; i++){ int &v = Node[top].Next[i]; if(v){ que.push(v); Node[v].fail = Node[Node[top].fail].Next[i]; }else v = Node[Node[top].fail].Next[i]; } } } }ac; char S[1111]; int dp[1111][1111]; int main(void) { mp['A'] = 0, mp['T'] = 1, mp['G'] = 2, mp['C'] = 3; int n, Case = 1; while(~scanf("%d", &n) && n){ ac.init(); for(int i=0; i<n; i++){ scanf("%s", S); ac.insert(S); } ac.BuildFail(); scanf("%s", S); int len = strlen(S); for(int i=0; i<=len; i++) for(int j=0; j<=ac.Size; j++) dp[i][j] = 2333; dp[0][0] = 0; for(int i=0; i<len; i++){ for(int j=0; j<ac.Size; j++){ if(dp[i][j] != 2333){ for(int k=0; k<4; k++){ int newi = i+1; int newj = ac.Node[j].Next[k]; if(!ac.Node[newj].flag){ dp[newi][newj] = min(dp[newi][newj], dp[i][j] + (k != mp[S[i]]) ); } } } } } int ans = 2333; for(int i=0; i<ac.Size; i++) ans = min(ans, dp[len][i]); printf("Case %d: ", Case++); if(ans != 2333) printf("%d\n", ans); else puts("-1"); } return 0; }
HDU 2296 Ring ( Trie图 && DP && DP状态记录)
题意 : 给出 m 个单词,每一个单词有一个权重,如果一个字符串包含了这些单词,那么意味着这个字符串拥有了其权重,问你构成长度为 n 且权重最大的字符串是什么 ( 若有权重相同的,则输出最短且字典序最小的 )
DP[i][j] 为构建了长度为 i 且最后一个字符为 j 的字符串最大权重,由于每一个状态都对应一个字符串,所以再构建一个三维字符数组 s[i][j][k] 表示当前 i、j 状态下具体的字符串为 s[i][j][0~k-1],那么状态转移方程就是
DP[i+1][ Trie[j][k] ] = max( DP[i+1][ Trie[j][k] ] , DP[i][j] + Trie[j][k].val )
( Trie[j][k] 代表 j 状态可以一步转移到 k状态
在状态转移的时候需要时时更新 s[i][j][k] 这个三维数组,当取得更优值的时候需要更新,最后只要在DP的过程当中记录最优的权重、状态i、j下标然后DP结束后输出即可

#include<string.h> #include<stdio.h> #include<queue> using namespace std; const int Max_Tot = 1200; const int Letter = 26; int dp[55][1200]; char s[55][1200][55];///存储每一个状态所代表的具体字符串 struct Aho{ struct StateTable{ int Next[Letter]; int fail, val; }Node[Max_Tot]; int Size; queue<int> que; inline void init(){ while(!que.empty()) que.pop(); memset(Node[0].Next, 0, sizeof(Node[0].Next)); Node[0].fail = Node[0].val = 0; Size = 1; } inline void insert(char *s, int val){ int now = 0; for(int i=0; s[i]; i++){ int idx = s[i] - 'a'; if(!Node[now].Next[idx]){ memset(Node[Size].Next, 0, sizeof(Node[Size].Next)); Node[Size].fail = Node[Size].val = 0; Node[now].Next[idx] = Size++; } now = Node[now].Next[idx]; } Node[now].val = val; } inline void BuildFail(){ Node[0].fail = 0; for(int i=0; i<Letter; i++){ if(Node[0].Next[i]){ Node[Node[0].Next[i]].fail = 0; que.push(Node[0].Next[i]); }else Node[0].Next[i] = 0; } while(!que.empty()){ int top = que.front(); que.pop(); Node[top].val += Node[Node[top].fail].val;///这里需要注意! for(int i=0; i<Letter; i++){ int &v = Node[top].Next[i]; if(v){ que.push(v); Node[v].fail = Node[Node[top].fail].Next[i]; }else v = Node[Node[top].fail].Next[i]; } } } }ac; char tmp[111][55]; int main(void) { int nCase; scanf("%d", &nCase); while(nCase--){ int n, m; scanf("%d %d", &n, &m); for(int i=0; i<m; i++) scanf("%s", tmp[i]); int tmpVal; ac.init(); for(int i=0; i<m; i++){ scanf("%d", &tmpVal); ac.insert(tmp[i], tmpVal); } ac.BuildFail(); for(int i=0; i<=n; i++){///将所有DP的值赋为 -1 for(int j=0; j<ac.Size; j++){ dp[i][j] = -1; s[i][j][0] = '\0'; } } dp[0][0] = 0;///定义初始状态 char str[60]; int ii, jj, MaxSum; ii = jj = MaxSum = 0; for(int i=0; i<n; i++){ for(int j=0; j<ac.Size; j++){ if(dp[i][j] >= 0){///如果当前dp值不是初始状态则进入if,否则其dp值毫无意义,直接跳过 for(int k=25; k>=0; k--){///一开始我是想谋求字典序最小而从后往前,但是WA一发后我发现我错了,实际上顺序不重要 int newi = i+1; int newj = ac.Node[j].Next[k]; int sum = dp[i][j] + ac.Node[ newj ].val; if(sum > dp[newi][newj]){ dp[newi][newj] = sum; strcpy(s[newi][newj], s[i][j]); int len = strlen(s[i][j]); s[newi][newj][len] = k+'a'; s[newi][newj][len+1] = '\0'; }else if(sum == dp[newi][newj]){///谋求字典序最小应该实在dp值相等情况下 strcpy(str, s[i][j]); int len = strlen(str); str[len] = 'a'+k; str[len+1] = '\0'; if(strcmp(str, s[newi][newj]) < 0) strcpy(s[newi][newj], str); } if(dp[newi][newj] >= MaxSum){///更新一下最终的答案 if(dp[newi][newj] == MaxSum){ int L1 = strlen(s[newi][newj]); int L2 = strlen(s[ii][jj]); if(L1<=L2 && strcmp(s[newi][newj], s[ii][jj])<0) ii = newi, jj = newj; }else{ MaxSum = dp[newi][newj]; ii = newi, jj = newj; } } } } } } if(MaxSum <= 0) puts("");///如果最后权值依旧是 0 那么输出空串 else puts(s[ii][jj]); } return 0; }
小心得: 对于AC自动机+dp 的这类题型 dp往往都是 dp[i][j] ,i表示长度,j表示在trie图中的节点 。 但有些题目是需要增加一些条件去维护的,但是也是在dp[i][j] 的基础上面去添加限制的dp[i][j][]
对于只是求 是否包含模式串的这类条件(注意不能具体包含多少个),ac自动机往往是在完全图上面做点东西的




