关于线段树or 树状树状 在二维平面搞事情!Orz
第一式:https://ac.nowcoder.com/acm/contest/143/I
题意:
有 n 个点,一个点集 S 是好的,当且仅当对于他的每个子集 T,存在一个右边无限长的矩形,使得这个矩形包含了 T,但是和 S-T 没有交
求这 n 个点里有几个好的点集
1<=n<=10^5

1):当只选取1个点时,我们可以发现,任何一个点都满足题意。
2):当我们选取2个点时,我们可以发现如果要满足一个无限向右的矩形只框住一个点,当且仅当两个点的纵坐标不相同。因此,对于选2个点的总的方案数等于C(n,2)-C(纵坐标相同的个数,2)
3):当我们选3个点的时候(假设三个点为a,b,c),我们可以发现,当我们选取{a,b}作为子集,倘如第三个点c在{a,b}的右边,则我们发现由{a,b}组成的矩形一定包含{c},故不成立。因此{c}必定在{a,b}的左边,即当且仅当三个点的能够构成一个'<'号的形式才能够符合题意。
4):当选4个点及以上时,我们发现不管怎么样摆,均不可能出现3)的情况,故4个点以上的点是不合理的。
因此现在我们只需要处理的就是3)中的情况。对于3)的情况。我们只要求出在第i个点之前,有多少个点的x坐标比当前点大(记位below),再求出在第i个点之后有多少个点的x坐标比当前点大(记位above),那么对于第i个点而言,该点的方案数即为below*above了。
而对于below和above值的维护,我们需要先将y坐标进行离散化,然后将数组按照x坐标进行排序,然后用树状数组对区间进行维护即可。
现在问题的转化为在平面上有多少个不同的3对点集可以构成 "<" 的形状
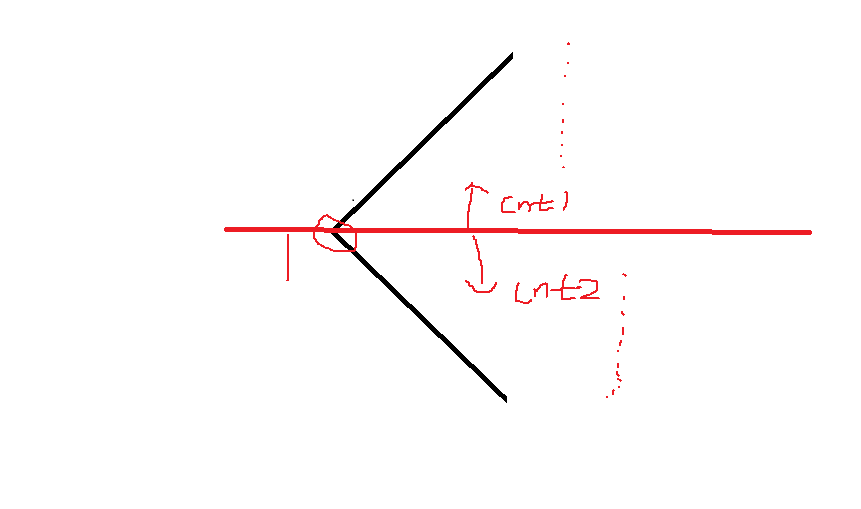
现在观察此图可以发现:
对于包括点1的点集的情况无非就是 在点1上面的点与在点1下面的点来构成,那总的答案就一个组合的问题 cnt1*xcnt2;
所以我们就要只要在点1上面的点的个数与在点一下面点的个数(还要保证是在点1的右边)
所以很自然的想到对x排序,然后从x大开始便利(因为比当前点的 x小的点是没有价值的),用树状树状维护一个y上面的前缀和既可

#include<bits/stdc++.h> using namespace std; #define ll long long const int mod = 998244353; const int maxn=100010; ll n; struct no { int x,y; }a[maxn]; int tree[maxn*4],b[maxn]; ll box[maxn]; void add(int x , int c) { while(x<=n) { tree[x]+=c; x+=(x&(-x)); } } int sum(int x) { int ret=0; while(x) { ret+=tree[x]; x-=(x&(-x)); } return ret; } bool cmp(no a , no b) { return a.x>b.x; } int main() { scanf("%lld",&n); for(int i=1 ; i<=n ; i++) { scanf("%d%d",&a[i].x,&a[i].y); b[i]=a[i].y; } sort(b+1,b+1+n); for(int i=1 ; i<=n ; i++) { a[i].y=lower_bound(b+1,b+1+n,a[i].y)-b; box[a[i].y]++; } ll ans=n+n*(n-1)/2; ///统计一个点和两个点的情况 for(int i=1 ; i<=n ; i++) ans-=box[i]*(box[i]-1)/2; ///减去两个点有相同的y ans=(ans+mod)%mod; ///统计 "<" 的情况 int L=1; sort(a+1,a+1+n,cmp); for(int i=1 ; i<=n ; i++) { ll down=sum(a[i].y-1); ll up=sum(n)-sum(a[i].y); ans=(ans+down*up)%mod; if(a[i].x!=a[i+1].x) { for(;L<=i ; L++) add(a[L].y,1); } } printf("%lld\n",ans); return 0; }
第二式:http://codeforces.com/contest/1191/problem/F
题意: 给出在二维平面上的点,问有多少个上面无限延长的矩阵是不同的 , 不同的定义为矩阵里面的点集是不同的
分析:这需要对x,y进行一个离散化的操作:
注意到其实从上往下一行一行扫过去,每次必须新增的元素才是新的集合,那很容易想到一个不重不漏的办法就是每次计算“以点p[i]为加进去的新点中的结束的集合”,那么假设一开始p[i]的左侧有cntl个点,那么显然有(cntl+1)条线在p[i]的左侧,而p[i]的右侧有cntr个点,也是(cntr+1)条线。
这个cntl显然就是query(1,p[i].x-1),而右侧则是query(p[i].x+1,p[i+1].x-1),因为不能包含同y的下一个点p[i+1],而其中,上面的点选法也会产生区别。
这个线段树的更新操作是赋值而不是加+1 , (因为如果同一条竖线上有多个点那其实排序去选择也只有一个价值而已)
那么每层加入一个正无穷也就是xn+1就可以了。
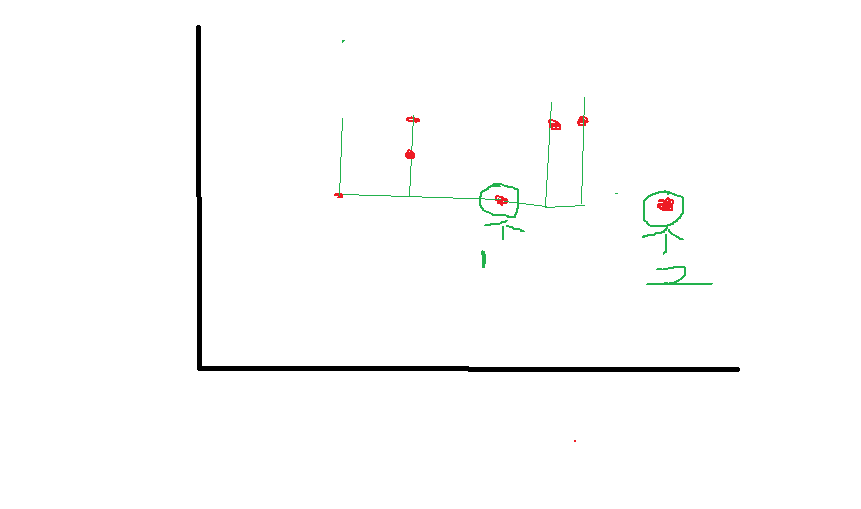
结合这图可以很容易看懂线段树的操作:1点的答案为(3*3) , 同时也可以理解为什么右侧是query(p[i].x+1,p[i+1].x-1),而不是说从当前点到最右面 , 想象一下,如果点1和点2右边的价值都是如此计算,那必然会存在重复计算。

#include<bits/stdc++.h> using namespace std; typedef long long ll; int n; struct Point { int x, y; bool operator<(const Point &p)const { return y == p.y ? x<p.x: y>p.y; //y从上到下,x从左到右 } } p[200005]; int x[200005]; int y[200005]; ll sum; const int MAXM = 200000; int st[(MAXM << 2) + 5]; inline void push_up(int o) { st[o] = st[o << 1] + st[o << 1 | 1]; } void build(int o, int l, int r) { if(l == r) { st[o] = 0; } else { int m = (l + r) >> 1; build(o << 1, l, m); build(o << 1 | 1, m + 1, r); push_up(o); } } void update(int o, int l, int r, int x, int v) { if(l == r) { //不是加,是赋值,同x的点是没有差别的 st[o] = v; return; } else { int m = (l + r) >> 1; if(x <= m) update(o << 1, l, m, x, v); else if(x >= m + 1) update(o << 1 | 1, m + 1, r, x, v); push_up(o); } } int query(int o, int l, int r, int a, int b) { if(b < a) return 0; else if(a <= l && r <= b) { return st[o]; } else { int m = (l + r) >> 1; int ans = 0; if(a <= m) ans = query(o << 1, l, m, a, b); if(b >= m + 1) ans += query(o << 1 | 1, m + 1, r, a, b); return ans; } } int vx[200005], vxtop; int main() { #ifdef Yinku freopen("Yinku.in", "r", stdin); //freopen("Yinku.out", "w", stdout); #endif // Yinku while(~scanf("%d", &n)) { for(int i = 1; i <= n; i++) { scanf("%d%d", &p[i].x, &p[i].y); x[i] = p[i].x; y[i] = p[i].y; } sort(x + 1, x + 1 + n); int xn = unique(x + 1, x + 1 + n) - (x + 1); sort(y + 1, y + 1 + n); int yn = unique(y + 1, y + 1 + n) - (y + 1); for(int i = 1; i <= n; i++) { p[i].x = lower_bound(x + 1, x + 1 + xn, p[i].x) - x; p[i].y = lower_bound(y + 1, y + 1 + yn, p[i].y) - y; //从1开始分配新的坐标 //printf("(%d,%d)\n", p[i].x, p[i].y); } sort(p + 1, p + 1 + n); //扫描线 sum = 0; build(1, 1, xn + 1); int beg = 1, cur = 1; while(beg <= n) { vxtop = 0; while(p[cur].y == p[beg].y) { update(1, 1, xn + 1, p[cur].x, 1); vx[++vxtop] = p[cur].x; /* //点是不会重合的,那包含这个最左侧的点的都是全新集合 int cntl = query(1, 1, xn, 1, p[cur].x - 1); //在这个点的左侧有cntl个x不同的点,那就有cntl+1个位置 //sum += (cntl + 1); X //是以这个点为右侧边界的,所以右侧没得选 X */ //该层y中是以这个x点为右侧边界,但是两个x点之间的上层y也是可选的 cur++; } vx[++vxtop] = xn + 1; for(int i = 1; i <= vxtop - 1; i++) { //该层最右端的新点为vx[i]的数量 int cntl = query(1, 1, xn + 1, 1, vx[i] - 1); ///同层或者上层数量 int cntr = query(1, 1, xn + 1, vx[i] + 1, vx[i + 1] - 1); ///在vx[i] + 1, vx[i + 1] - 1 横坐标范围 上层的数量, sum += 1ll * (cntl + 1) * (cntr + 1); // printf("sum=%lld vx[i]=%d cnt1=%d cnt2=%d\n",sum,vx[i],cntl,cntr,); } beg = cur; } printf("%lld\n", sum); } }
第三式:http://codeforces.com/contest/1194/problem/E
题意:
给N条线段 , 线段只有垂直或者水平 , 问有多少个不同的4个线段集合构成(
h1和h2是水平;
v1和v2是垂直的;
h1段与v1段相交;
h2段与v1段相交;
h1段与v2段相交;
h2段与v2段相交。
) 也就是一个#差不多:
分析:在代码里面有注释了, 觉得看了代码理解起来不难

#include<bits/stdc++.h> using namespace std; #define ll long long const int N=1e6+5; int c[N]; int n; int lowbit(int x) { return x&(-x); } void add(int i , int x) { while(i<N) { c[i]+=x; i+=lowbit(i); } } int sum(int i) { int ans=0; while(i) { ans+=c[i]; i-=lowbit(i); } return ans; } struct svno { int y1,y2,x; bool operator <(const svno& Q) const { return x<Q.x; } }; struct hvno { int x1,x2,y; bool operator <(const hvno& Q) const { return x2<Q.x2; } }; vector<svno> SV; vector<hvno>HV; int main() { while(~scanf("%d",&n)) { memset(c,0,sizeof(c)); HV.clear(); SV.clear(); ll ans=0; for(int i=0 ; i<n ; i++) { int x1,x2,y1,y2; scanf("%d%d%d%d",&x1,&y1,&x2,&y2); x1+=5001 , x2+=5001 , y1+=5001 , y2+=5001; if(x1==x2) { if(y1>y2) swap(y1,y2); SV.push_back({y1,y2,x1}); } else { if(x1>x2) swap(x1,x2); HV.push_back({x1,x2,y1}); } sort(SV.begin(),SV.end()); sort(HV.begin(),HV.end()); } vector<int>temp; int lensv=SV.size(); int lenhv=HV.size(); ///枚举第一条竖线 for(int i=0 ; i<lensv ; i++) { ///加入符合的横线 temp.clear(); for(int j=0 ; j<lenhv ; j++) { if(HV[j].x1<=SV[i].x&&HV[j].x2>=SV[i].x&&HV[j].y>=SV[i].y1&&HV[j].y<=SV[i].y2) { temp.push_back(j); add(HV[j].y,1); } } ///枚举第二条竖线 int lent=temp.size(); int k=0; for(int j=i+1 ; j<lensv ; j++) { ///删除枚举的第二条竖线时不满足条件的横线 ///其实只要考虑横线在枚举的竖线的左边的情况 for( ; k<lent ; k++) { int k_id=temp[k]; if(HV[k_id].x2<SV[j].x) { add(HV[k_id].y,-1); } else break; } ///计算价值 ll cnt=sum(SV[j].y2)-sum(SV[j].y1-1); ans+=cnt*(cnt-1)/2; // cout<<cnt<<endl; } ///删除剩余的横线 for(;k<lent;k++) { add(HV[temp[k]].y,-1); } }printf("%lld\n",ans); } }
总的来说这种题目不难 , 有时间还是可以想到一些东西的 。Orz




