HDU 6189 Law of Commutation(规律)

题意：

给定n,a，求区间 [ 1 , 1<<n ] 的数b 满足 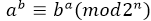的个数

 

分析：打出暴力程序可以发现当a为奇数的时候结果为一；

当a为偶时 ， a^b=2^(k+b)mod 2^n ; 结果肯定为0 ； 

那就有b^a mod 2^n=0 ; 则 b也为偶数 ，在分析：

然后分类讨论 b <= n时暴力搞搞

 b > n时 就需要满足 b^a % (2^n)等于0了

 同理就要满足b^a = 2^a * k^a % (2^n)  = 0 那么假设k有x个2 使得(x + 1) * a >= n就好了

 

#include <stdio.h>
#include <algorithm>
#include <iostream>
using namespace std;
typedef long long ll;

ll m;
ll pow_mod(ll x, ll y)
{
    ll res = 1;
    while(y)
    {
        if(y & 1) res = res * x % m;
        y >>= 1;
        x = x * x % m;
    }
    return res;
}

int main()
{
    ll n, a;
    while(~scanf("%lld%lld", &n, &a))
    {
        m = (1 << n);
        if(a & 1)
        {
            puts("1");
            continue;
        }
        else
        {
            ll ans = 0;
            for(int i = 1; i <= n; i++)
            {
                ll o = pow_mod(a, i);
                ll u = pow_mod(i, a);
                if(o == u) ans++;
            }

            if(a > n) ans += m / 2 - n / 2;
            else
            {
                ll p;
                if(n % a != 0) p = n / a + 1;
                else p = n / a;

                p = (1LL << p);
                ans += m / p - n / p;
            }
            printf("%lld\n", ans);
        }
    }
    return 0;
}