分类算法-1.准确度的问题

分类准确度的问题

假如有一个癌症预测系统，输入体检信息，可以判断是否有癌症，准确度为99.9%，这个系统是好还是坏？
如果癌症产生的概率本来就只有0.1%，那么即使不采用此预测系统，对于任何输入的体检信息，都预测所有人都是健康的，即可达到99.9%的准确率。如果癌症产生的概率本来就只有0.01%，预测所有人都是健康的概率可达99.99%，比预测系统的准确率还要高，这种情况下，准确率99.9%的预测系统是失败的。
由此可以得出结论：对于极度偏斜（Skewed Data）的数据，只使用分类准确度是远远不够的。

混淆矩阵 Confusion Matrix

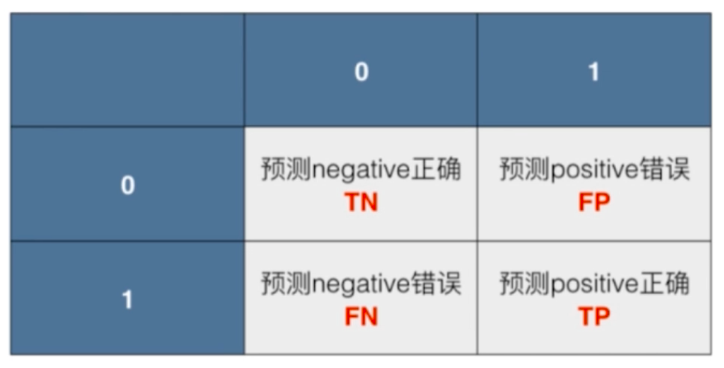
对于二分类问题：

行代表真实值，列代表预测值
0代表阴性(Negative),1代表阳性(Positive)
预测阳性正确TP,预测阳性错误FP,预测阴性正确TN,预测阴性错误FN

精准率：\(Precision = \frac{TP}{TP+FP}\)
召回率：\(Recall = \frac{TP}{TP+FN}\)，

在癌症预测系统中，精准率表示预测得癌症的总人数中预测对的比例,召回率表示实际得癌症的总人数中预测对的比例

假设有10000个人，有10个人患有癌症，我们预测所有的人都是健康的，得到混淆矩阵：

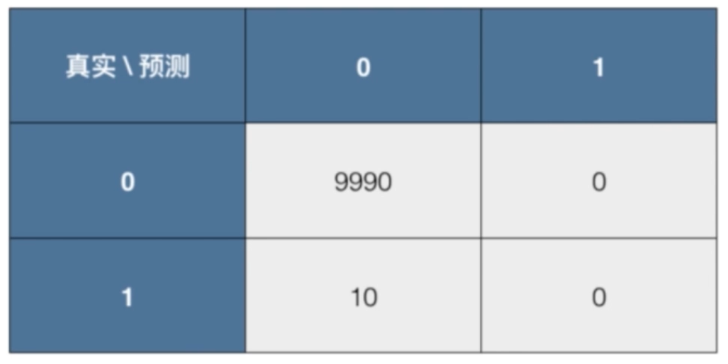
算法各指标计算：

准确率=99.9%
精准率=0/(0+0)无意义
召回率=0/(10+0)=0

手写数据集下实现混淆矩阵、精准率和召回率

加载数据集

import numpy
from sklearn import datasets

digits = datasets.load_digits()
x = digits.data
y = digits.target.copy()

# 处理数据，使数据极度偏斜
y[digits.target==9] = 1
y[digits.target!=9] = 0

# 测试训练数据分离
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(x,y,random_state=666)

# 加载逻辑回归算法
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(x_train,y_train)
y_predict = log_reg.predict(x_test)

混淆矩阵

def TN(y_true,y_predict):
    assert len(y_true)==len(y_predict)
    return numpy.sum((y_true==0)&(y_predict==0))
    
def TP(y_true,y_predict):
    assert len(y_true)==len(y_predict)
    return numpy.sum((y_true==1)&(y_predict==1))

def FN(y_true,y_predict):
    assert len(y_true)==len(y_predict)
    return numpy.sum((y_true==1)&(y_predict==0))

def FP(y_true,y_predict):
    assert len(y_true)==len(y_predict)
    return numpy.sum((y_true==0)&(y_predict==1))

def confusion_matrix(y_true,y_predict):
    assert len(y_true)==len(y_predict)
    return numpy.array([
        [TN(y_true,y_predict),FP(y_true,y_predict)],
        [FN(y_true,y_predict),TP(y_true,y_predict)]
    ])

精准率和召回率

def precision_score(y_true,y_predict):
    tp = TP(y_test,y_predict)
    fp = FP(y_test,y_predict)
    try:
        return tp/(fp+tp)
    except:
        return 0

def recall_score(y_true,y_predict):
    tp = TP(y_test,y_predict)
    fn = FN(y_test,y_predict)
    try:
        return tp/(fn+tp)
    except:
        return 0

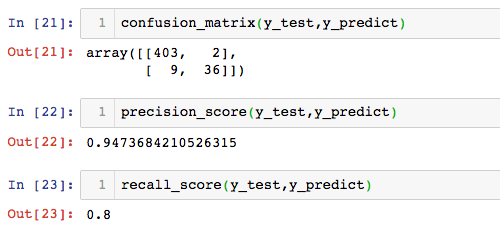
scikit-learn中的混淆矩阵及其精准率和召回率

from sklearn.metrics import confusion_matrix,precision_score,recall_score