逻辑回归-6.解决多分类问题

逻辑回归是使用回归的方式来解决分类问题。之前说过，逻辑回归只能解决二分类问题，为了解决多分类问题，可以使用OVR和OVO方法

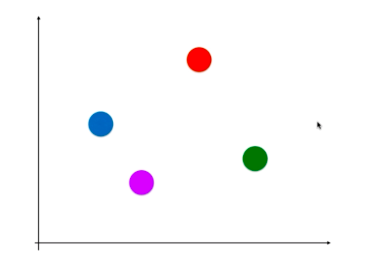
• OVR(One Vs Rest)
  某个分类算法有N类，将某一类和剩余的类比较作为二分类问题，N个类别进行N次分类，得到N个二分类模型，给定一个新的样本点，求出每种二分类对应的概率，概率最高的一类作为新样本的预测结果。
  

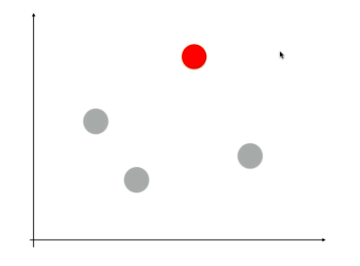
• OVO(One Vs One)
  某个分类算法有N类，将某一类和另一类比较作为二分类问题，总共可分为\(C^2_n\)种不同的二分类模型，给定一个新的样本点，求出每种二分类对应的概率，概率最高的一类作为新样本的预测结果。
  

加载鸢尾花数据集（数据集有三类结果）：

import numpy
from sklearn import datasets
from sklearn.model_selection import train_test_split

iris = datasets.load_iris()
# 为了数据可视化，只取数据集的前两个特征
x = iris.data[:,:2]
y = iris.target
x_train,x_test,y_train,y_test = train_test_split(x,y,random_state=666)

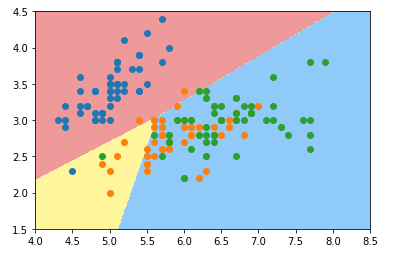
scikit-learn中默认支持多分类，且多分类方法默认为OVR

from sklearn.linear_model import LogisticRegression

log_reg = LogisticRegression()
log_reg.fit(x_train,y_train)

画出决策边界：

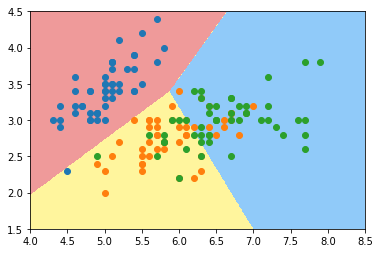
使用OVO多分类方法：

log_reg2 = LogisticRegression(multi_class='multinomial',solver='newton-cg')
log_reg2.fit(x_train,y_train)

scikit-learn中的OVR和OVO类¶

from sklearn.multiclass import OneVsRestClassifier,OneVsOneClassifier

# 使数据所有的特征值参与运算
x = iris.data
y = iris.target
x_train,x_test,y_train,y_test = train_test_split(x,y,random_state=666)

• OVR

log_reg1 = LogisticRegression()
OVR = OneVsRestClassifier(log_reg1)
OVR.fit(x_train,y_train)

准确率：

• OVO

log_reg2 = LogisticRegression()
OVR = OneVsRestClassifier(log_reg2)
OVR.fit(x_train,y_train)

准确率：