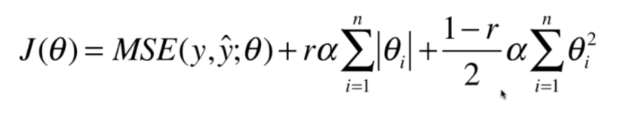多项式回归-4.模型正则化
方差偏差权衡(Bias Variance Trade off)
模型误差 = 偏差(Bias)+方差(Variance)+不可避免的误差

导致偏差的主要原因:对问题本身的假设不正确!如:非线性数据使用线性回归(欠拟合 underfitting)
导致方差的主要原因:数据的一点点扰动都会较大地影响模型,使用的模型太复杂,如:高阶多项式回归(过拟合overfitting)
有一些算法通常是高方差的算法,如k近邻 。有一些算法通常是高偏差算法,如线性回归。非参数学习通常都是高方差算法,因为不对数据进行假设。参数学习通常都是高偏差算法,因为对数据有较强的假设
偏差和方差通常是矛盾的,降低偏差,会提高方差,降低方差,会提高偏差。
机器学习的主要挑战,来自于方差!,解决高方差的通常手段:
- 降低模型复杂度
- 减少数据维度,降噪
- 增加样本数
- 使用验证集
- 模型正则化
模型正则化 Regularization
模型正则化:限制参数的大小
回归之前的线性回归算法,我们的目标是找到一组\(\theta=(\theta_0,\theta_1,\theta_2,\theta _0,...,\theta _n)\) 使得损失函数:
尽可能小。其中 \(\hat y^{(i)} = \theta _0x^{(i)}_0 + \theta _1x^{(i)}_1 + \theta _2x^{(i)}_2 +...+ \theta _{n}x^{(i)}_n,x^{(i)}_0 \equiv 1\)
为了模型和样本无关,我们给式子除于m:
Ridge回归
加入模型正则化项\(\theta ^2\),使得损失函数:
尽可能小,这种模型回归的方式叫做岭回归
LASSO回归
加入模型正则化项\(\left | \theta \right |\),使得损失函数:
尽可能小,这种模型回归的方式叫做LASSO回归
$\alpha $为一个超参数,表示模型正则化在目标函数中的比例
代码实现
加载相应的库,并构造线性数据集
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures,StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.metrics import mean_squared_error
import numpy
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
numpy.random.seed(42)
x = numpy.random.uniform(-3,3,size=100)
X = x.reshape(-1,1)
y = 0.5 * x + 3 + numpy.random.normal(0,1,size=100)
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=666)
定义多项式回归和绘制图形函数:
def PolynomialRegression(degree,lin_reg):
return Pipeline([
("poly",PolynomialFeatures(degree)),
("std_scaler",StandardScaler()),
("line_reg",lin_reg)
])
def plot_model(model):
X_plot = numpy.linspace(-3,3,100).reshape(100,1)
y_plot = model.predict(X_plot)
plt.scatter(x,y)
plt.plot(X_plot[:,0],y_plot,color='r')
plt.axis([-3,3,0,6])
plt.show()
1.用多项式回归拟合,阶次为20(过拟合)
lin_reg = LinearRegression()
poly20_reg = PolynomialRegression(degree=20,lin_reg=lin_reg)
poly20_reg.fit(X_train,y_train)
y20_predict = poly20_reg.predict(X_test)
mean_squared_error(y_test,y20_predict)

均方误差高达167,说明此模型过拟合,对数据的泛化能力很差
绘制此模型
plot_model(poly20_reg)
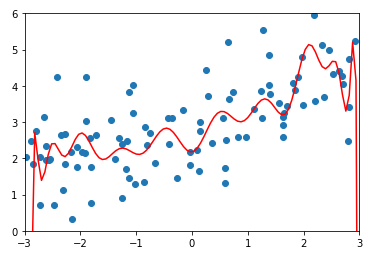
2.使用Ridge回归
from sklearn.linear_model import Ridge
def RidgeRegression(degree,alpha):
return Pipeline([
("poly",PolynomialFeatures(degree)),
("std_scaler",StandardScaler()),
("line_reg",Ridge(alpha=alpha))
])
\(\alpha = 0.0001\)时
ridge1_reg = RidgeRegression(degree=20,alpha=0.0001)
ridge1_reg.fit(X_train,y_train)
y1_predict = ridge1_reg.predict(X_test)
mean_squared_error(y_test,y1_predict)
均方误差:

绘制此模型
plot_model(ridge1_reg)
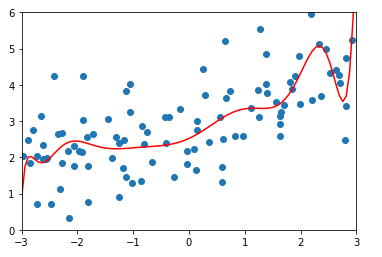
\(\alpha = 100\)时的均方误差及结果:

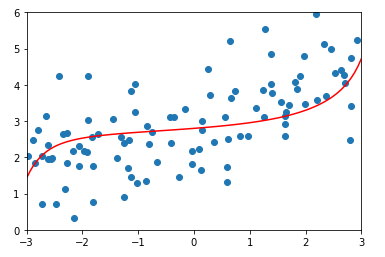
\(\alpha = 1000000\)时的均方误差及结果:

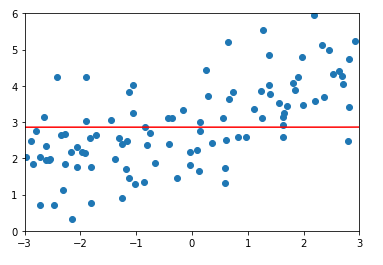
由此可以看出,当\(\alpha\)越来越大时,参数\(\theta\)对模型的影响程度越来越高,当\(\alpha\)无穷大时,为了目标函数尽可能小,\(\theta\)取值为0,此时多项式只有截距,数据为一条平行于X轴的直线。
3.使用LASSO回归
from sklearn.linear_model import Lasso
def LassoRegression(degree,alpha):
return Pipeline([
("poly",PolynomialFeatures(degree)),
("std_scaler",StandardScaler()),
("lasso_reg",Lasso(alpha=alpha))
])
\(\alpha = 0.01\)时
lasso1_reg = LassoRegression(degree=20,alpha=0.01)
lasso1_reg.fit(X_train,y_train)
y1_predict = lasso1_reg.predict(X_test)
均方误差以及结果:

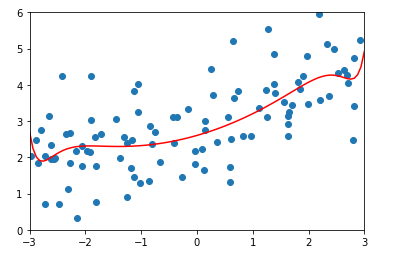
\(\alpha = 0.1\)时,均方误差以及结果:

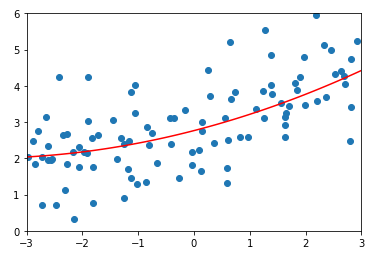
\(\alpha = 1\)时,均方误差以及结果:

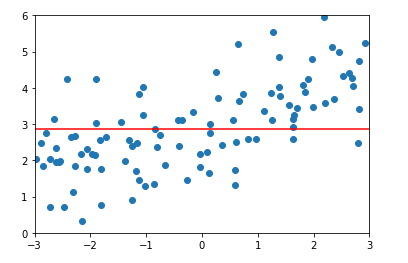
比较Ridge和LASSO
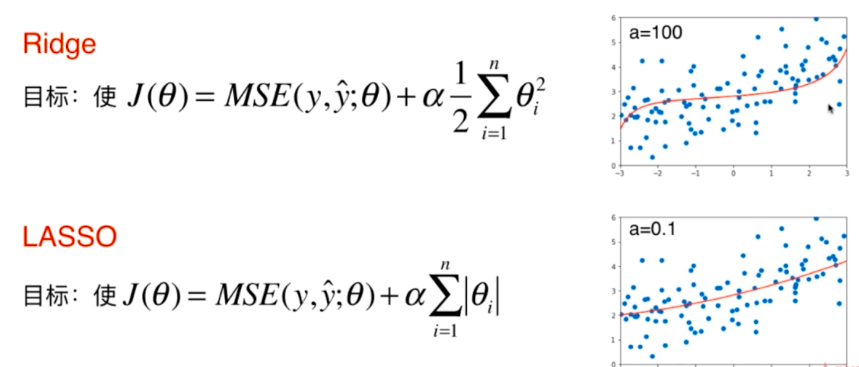
Lasso回归得到的曲线比Ridge回归得到的曲线更倾向于一条直线,通过直线和曲线的思考,可以发现,Ridge回归后的模型依然有很多特征前面是存在系数的,而Lasso回归后许多特征前面的系数\(\theta\)减小到0了,Lasso趋向于使得一部分\(\theta\)的值变为0,这个特性可作为特征选择用。
原理:当\(\theta\)取无穷时,目标函数被模型正则化项所主导,\(\theta^2\)和\(\left | \theta \right |\)在梯度下降的过程中,表现形式不一样。
弹性网
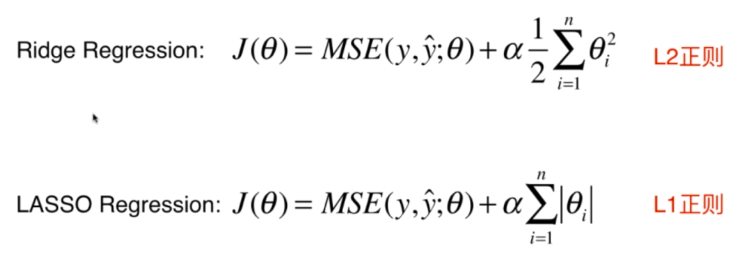
结合L1和L2的弹性网: