PCA-1.降维原理
主成分分析(Principal Component Analysis)
- 一个非监督的机器学习算法
- 主要用于数据的降维
- 通过降维,可以发现更易于人类理解的特征
- 其他应用:可视化,去噪
降维

上图为含有两个特征的样本空间,数据的维度为2,可以忽视一个不明显的特征,保留一个相对差距明显的特征进行降维
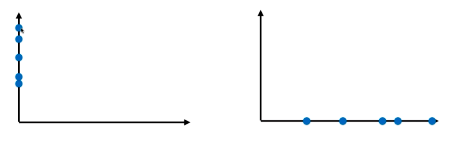
显然选择特征1效果好一点
我们也可以选择一条更适合的直线(方差最大),把所有的点映射到这个直线上,来达到降维的目的
方差定义:\(Var(x) = \frac{1}{m}\sum(x_i - \bar{x})^2\).

第一步:将所有样本的均值归0(demean)
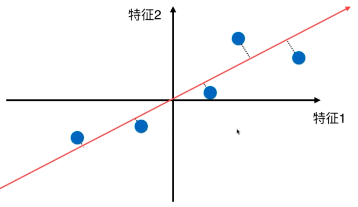
假设某轴\(w = (w1,w2)\),使得所有的样本映射到\(w\)上,有:
\[Var(X_p) = \frac{1}{m}\sum_{i=1}^{m}\left \| X^i_p \right \|^2最大
\]
其中\(X^i_p\)代表映射在此轴的样本
根据向量点乘的定义,又因为\(w\)是方向向量,膜为1 :
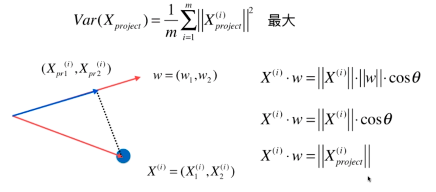
所以: $$\left | X^i_p \right | = X^i \cdot w$$
目标:求\(w\),使得:
\[Var(X_p) = \frac{1}{m}\sum_{i=1}^{m}(X^i \cdot w)^2 最大
\]
一个目标函数的最优问题,采用梯度上升法



