梯度下降法-6.调试梯度下降法

梯度下降法的准确性与调试

对于梯度下降法的使用，一个非常重要的步骤是求解我们定义的损失函数\(J\)在某个点\(\theta\)上的梯度值\(dJ\)，我们也花了很长时间来推导此公式，但是对于一些复杂的函数如非线性函数，求解梯度并不容易，在这种情况下，为了保证求解的梯度表达式正确，发现求解过程中的错误，需要进行梯度下降法的调试

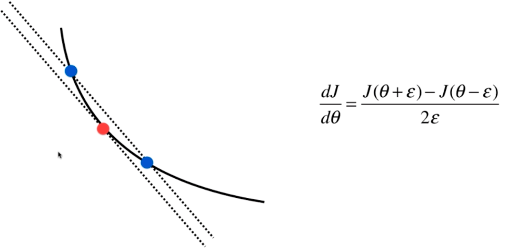
定义\(\theta=(\theta_0,\theta_1,\theta_2,\theta _0,...,\theta _n)\) ，对每一个\(\theta\)求导：

\[\Lambda J = (\frac{\partial J}{\partial \theta _0},\frac{\partial J}{\partial \theta _1},\frac{\partial J}{\partial \theta _2},...,\frac{\partial J}{\partial \theta _n}) \]

而其中：

\[\frac{\partial J}{\partial \theta _i} = \frac{J(\theta_i^+ )-J(\theta_i^-)}{2\varepsilon } =\frac{J(\theta_i +\varepsilon )-J(\theta_i -\varepsilon )}{2\varepsilon } \]

调试的过程：

构造数据集

import numpy
import matplotlib.pyplot as plt

numpy.random.seed(666)
X = numpy.random.random(size=(1000,10))
true_theta = numpy.arange(1,12)

X_b = numpy.hstack([numpy.ones((len(X),1)),X])
y = X_b.dot(true_theta) + numpy.random.normal(size=1000)

定义损失函数和梯度下降方法：

def J(theta,X_b,y):   #损失函数的表达式
    return numpy.sum((y - X_b.dot(theta))**2)/len(X_b)

def dJ_math(theta,X_b,y):
    return X_b.T.dot(X_b.dot(theta)-y)*2/len(X_b)

def dJ_Debug(theta,X_b,y,epsilon=0.01):
    m = len(theta)
    res = numpy.empty(m)
    for i in range(m):
        theta_1 = theta.copy()
        theta_1[i] += epsilon
        theta_2 = theta.copy()
        theta_2[i] -= epsilon
        res[i] = (J(theta_1,X_b,y)-J(theta_2,X_b,y))/(2*epsilon)
    return res

定义梯度下降过程：

def gradient_descent(dJ,X_b,y,init_theta,eta,n_iters=1e4,espilon=1e-8):
    
    theta = init_theta
    i_iters = 0
    
    # n_iters 表示梯度下降的次数，超过这个值，有可能算法不收敛，退出
    while n_iters>i_iters: 
        gradient = dJ(theta,X_b,y)  #偏导数
        last_theta = theta
        theta = theta - eta * gradient  #梯度下降，向极值移动   
        if abs(J(theta,X_b,y) - J(last_theta,X_b,y)) < espilon:
            break
        i_iters += 1 
    # 返回求出的theta值
    return theta
    
init_theta = numpy.zeros(X_b.shape[1])
eta=0.01

使用调试的方法梯度下降，查看\(\theta\)值和计算时间

%time theta = gradient_descent(dJ_Debug,X_b,y,init_theta,eta,n_iters=1e4,espilon=1e-8)

使用数学推导的方法梯度下降，查看\(\theta\)值和计算时间

%time theta = gradient_descent(dJ_math,X_b,y,init_theta,eta,n_iters=1e4,espilon=1e-8)

通过结果比较，我们能确定数学推导的求梯度公式的正确性。