梯度下降法-5.随机梯度下降法
之前所讲解的梯度下降法是批量梯度下降法(Batch Gradient Descent),我们将要优化的损失函数在某一点\(\theta\)的梯度值准确的求出来
\[\Lambda J = \begin{bmatrix}
\frac{\partial J}{\partial \theta _0} \\
\frac{\partial J}{\partial \theta _1} \\
\frac{\partial J}{\partial \theta _2} \\
... \\
\frac{\partial J}{\partial \theta _n}
\end{bmatrix} = \frac{2}{m}\begin{bmatrix}
\sum(X^{(i)}_b\theta - y^{(i)}) \cdot X_0^{(i)}\\
\sum(X^{(i)}_b\theta - y^{(i)}) \cdot X_1^{(i)}\\
\sum(X^{(i)}_b\theta - y^{(i)}) \cdot X_2^{(i)}\\
...\\
\sum(X^{(i)}_b\theta - y^{(i)}) \cdot X_3^{(i)}
\end{bmatrix} = \frac{2}{m}X_b^T \cdot (X_b\theta -y) \]
通过以上公式可以看出,每一项都要将所有的样本进行计算,如果样本非常大,那么计算梯度本身相当耗时,所以引入了随机梯度下降法。
随机梯度下降法(Stochastic Gradient Descent)
假设有m个样本,我们随机挑选出一个样本,进行搜索
\[\Lambda J = \begin{bmatrix}
\frac{\partial J}{\partial \theta _0} \\
\frac{\partial J}{\partial \theta _1} \\
\frac{\partial J}{\partial \theta _2} \\
... \\
\frac{\partial J}{\partial \theta _n}
\end{bmatrix} = 2\begin{bmatrix}
(X^{(i)}_b\theta - y^{(i)}) \cdot X_0^{(i)}\\
(X^{(i)}_b\theta - y^{(i)}) \cdot X_1^{(i)}\\
(X^{(i)}_b\theta - y^{(i)}) \cdot X_2^{(i)}\\
...\\
(X^{(i)}_b\theta - y^{(i)}) \cdot X_3^{(i)}
\end{bmatrix} = 2(X_b^{(i)})^T \cdot (X_b^{(i)}\theta -y_i) \]
其搜索过程如下图所示:
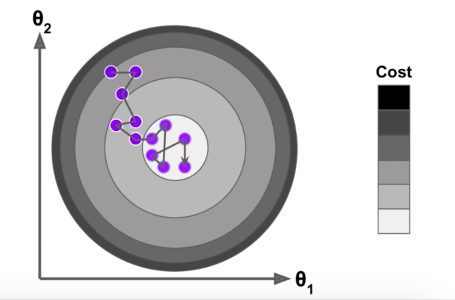
因为随机的不可预知性,搜索过程中,不可能到达最小值这个固定的位置,但是会在附近徘徊,当样本m比较大时,可以用一定的精度来换取时间,而学习率$\eta $ 的选取至关重要,学习率$\eta $应该随着循环次数的增加而逐渐变小:
\[\eta = \frac{a}{iters +b}
\]
iters为循环次数,a,b为两个超参数
验证随机梯度下降
构造数据集
import numpy
import matplotlib.pyplot as plt
m = 100000
x = numpy.random.normal(size=m)
X = x.reshape(-1,1)
y = 4. *x + 3. + numpy.random.normal(0.0,3.0,size=m)
定义梯度下降的过程
# 返回某个样本的梯度值
def dJ_Sgd(theta,X_b_i,y_i):
return X_b_i.T.dot(X_b_i.dot(theta)-y_i)*2
# 梯度下降的过程
def sgd(X_b,y,init_theta,n_iters,espilon=1e-8): #求导
t0 =5
t1=50
def learn_rate(t): # 定义学习率
return t0/(t+t1)
theta = init_theta
m = len(X_b)
# 梯度下降 n_iters 次
for cur_iters in range(n_iters):
# m个样本中随机找出一个样本
rand_i = numpy.random.randint(m)
gradient = dJ_Sgd(theta,X_b[rand_i],y[rand_i])
theta = theta - gradient * learn_rate(n_iters*m +i)
return theta
测试,为了展现随机梯度下降法的威力,梯度下降次数取样本值的1/3时,求得的 \(\theta\) 值
%%time
X_b = numpy.hstack([numpy.ones((len(X),1)),X])
init_theta = numpy.zeros(X_b.shape[1])
theta = sgd(X_b,y,init_theta,n_iters=len(X_b)//3)
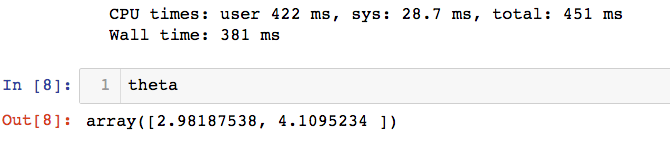
可以看出随机梯度下降法的计算次数少,但是准确率却很高
封装并查看真实的数据集中的效果
加载波士顿房产数据集
import numpy
import matplotlib.pyplot as plt
from sklearn import datasets
boston = datasets.load_boston()
X = boston.data
y = boston.target
X = X[y<50]
y = y[y<50]
对原始数据进行预处理:
# 训练 测试数据分离
from mylib.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,seed=666)
# 数据归一化
from sklearn.preprocessing import StandardScaler
Sd = StandardScaler()
Sd.fit(X_train)
X_train_stand = Sd.transform(X_train)
X_test_stand = Sd.transform(X_test)
加载封装的库,查看计算时间和准确率
from mylib.LineRegression import LineRegression
reg_2 = LineRegression()
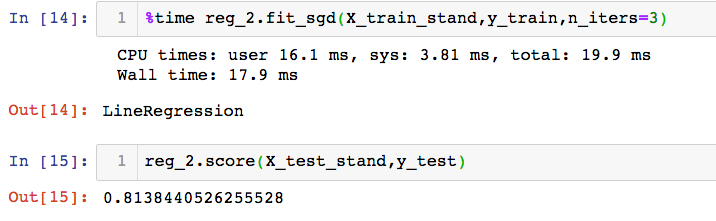
%time reg_2.fit_sgd(X_train_stand,y_train,n_iters=3)
reg_2.score(X_test_stand,y_test)
scikit-learn 中的 SGD
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(n_iters=50)
%time sgd_reg.fit(X_train_stand,y_train)
sgd_reg.score(X_test_stand,y_test)



