梯度下降法-3.实现线性回归中的梯度下降法

实现线性回归中的梯度下降法

构造数据集

import numpy
import matplotlib.pyplot as plt

# 设置随机数种子
numpy.random.seed(666)  
x = 2 * numpy.random.random(size=100)
y = x * 3. + 4. + numpy.random.normal(size=100)  #random.normal 为产生正太分布的噪点

#假设此样本有一个特征值，把100个数转化为100行，1列
X = x.reshape(-1,1)  

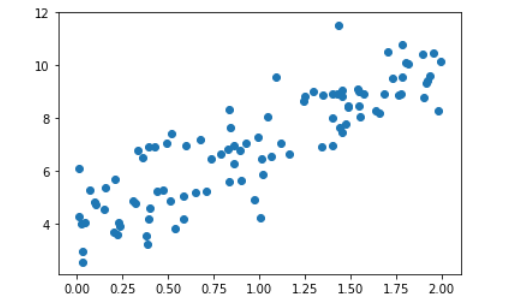
绘制此数据集：

plt.scatter(x,y)
plt.show()

使用梯度下降法训练

目标：使

\[ J = \frac{1}{m}\sum_{i=1}^{m}(y^{(i)} - \hat{y}^{(i)})^2 $$尽可能的小 $$\Lambda J = \begin{bmatrix} \frac{\partial J}{\partial \theta _0} \\ \frac{\partial J}{\partial \theta _1} \\ \frac{\partial J}{\partial \theta _2} \\ ... \\ \frac{\partial J}{\partial \theta _n} \end{bmatrix} = \frac{2}{m}\begin{bmatrix} \sum(X^{(i)}_b\theta - y^{(i)}) \\ \sum(X^{(i)}_b\theta - y^{(i)}) \cdot X_1^{(i)}\\ \sum(X^{(i)}_b\theta - y^{(i)}) \cdot X_2^{(i)}\\ ...\\ \sum(X^{(i)}_b\theta - y^{(i)}) \cdot X_3^{(i)} \end{bmatrix}\]

定义函数和导数的表达式

def J(theta,X_b,y):   #损失函数的表达式
    try:
        return numpy.sum((y - X_b.dot(theta))**2)/len(X_b)
    except:
        return float('inf') #返回float的最大值
   
def dJ(theta,X_b,y):  #求导
    #要返回的导数矩阵
    res = numpy.empty(len(theta))    
    
    res[0] = numpy.sum(X_b.dot(theta)-y)
    for i in range(1,len(theta)):
        res[i] = ((X_b.dot(theta)-y).dot(X_b[:,i]))
        
    return res*2/len(X_b)

定义梯度下降的算法过程

def gradient_descent(X_b,y,init_theta,eta,n_iters=1e4,espilon=1e-8):
    
    theta = init_theta
    i_iters = 0
    
    #n_iters 表示梯度下降的次数，超过这个值，有可能算法不收敛，退出
    while n_iters>i_iters: 
        gradient = dJ(theta,X_b,y)  #偏导数
        last_theta = theta
        theta = theta - eta * gradient  #梯度下降，向极值移动   
        if abs(J(theta,X_b,y) - J(last_theta,X_b,y)) < espilon:
            break
        i_iters += 1 
    # 返回求出的theta值
    return theta

构造初始参数，并进行梯度下降的过程：

X_b = numpy.hstack([numpy.ones((len(X),1)),X])
init_theta = numpy.zeros(X_b.shape[1])
eta = 0.01
theta = gradient_descent(X_b,y,init_theta,eta)

求得的theta值

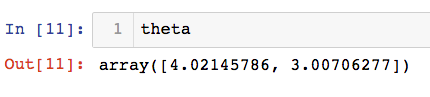
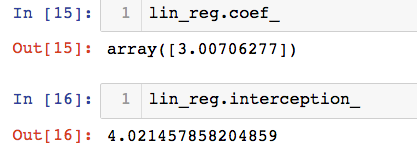
创建数据集时，截距为4，斜率为3，由此可以看出，此梯度下降法成功的训练了此模型

算法的封装

def fit_gd(self,X_train,y_train,eta=0.01,n_iters=1e4):

		assert X_train.shape[0] == y_train.shape[0],\
			"size of x_train must be equal to the size of y_train"

		def J(theta,X_b,y):   
			try:
				return numpy.sum((y - X_b.dot(theta))**2)/len(X_b)
			except:
				return float('inf')  # 返回float的最大值

		def dJ(theta,X_b,y):  
			#要返回的导数矩阵
			res = numpy.empty(len(theta))    
	
			res[0] = numpy.sum(X_b.dot(theta)-y)
			for i in range(1,len(theta)):
				res[i] = ((X_b.dot(theta)-y).dot(X_b[:,i]))
			return res*2/len(X_b)

		def gradient_descent(X_b,y,init_theta,eta,n_iters,espilon=1e-8):
			theta = init_theta
			i_iters = 0
			while n_iters>i_iters:
				gradient = dJ(theta,X_b,y)  #偏导数
				last_theta = theta
				theta = theta - eta * gradient  #梯度下降，向极值移动
	
				if abs(J(theta,X_b,y) - J(last_theta,X_b,y)) < espilon:
					break
				i_iters += 1
			return theta

		X_b = numpy.hstack([numpy.ones((len(X_train),1)),X_train])

		init_theta = numpy.zeros(X_b.shape[1])
		self._theta = gradient_descent(X_b,y_train,init_theta,eta,n_iters)

		self.coef_ = self._theta[1:]    #系数
		self.interception_ = self._theta[0] #截距
		return self

封装后调用：

from mylib.LineRegression import LineRegression
lin_reg = LineRegression()
# 用梯度下降法训练
lin_reg.fit_gd(X,y)