梯度下降法-2.线性回归中的梯度下降法
多元线性回归中使用梯度下降
在多元线性回归中,我们的目标是找到一组\(\theta=(\theta_0,\theta_1,\theta_2,\theta _0,...,\theta _n)\) 使得损失函数:
\[J = \sum_{i=1}^{m}(y^{(i)} - \hat{y}^{(i)})^2
\]
尽可能小。其中 $$\hat y^{(i)} = \theta _0x^{(i)}_0 + \theta _1x^{(i)}_1+ \theta _2x^{(i)}_2+...+\theta _{n}x{(i)}_n,x_0\equiv 1 $$
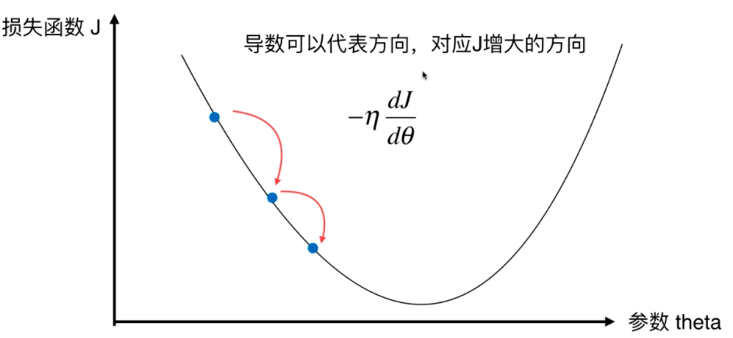
多元线性回归的导数$$\Lambda J = (\frac{\partial J}{\partial \theta _0},\frac{\partial J}{\partial \theta _1},\frac{\partial J}{\partial \theta _2},...,\frac{\partial J}{\partial \theta _n})$$
对各个\(\theta_i\)求偏导数:
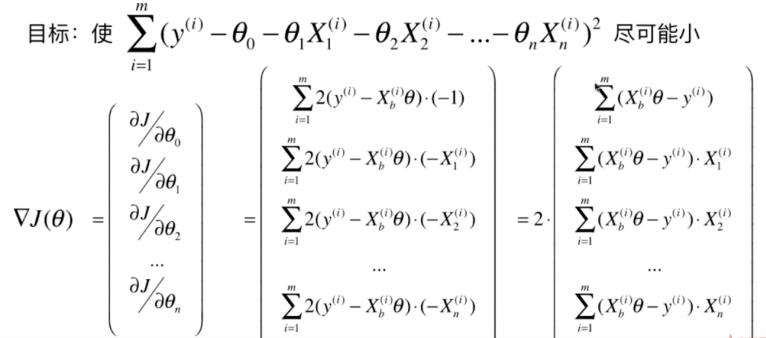
求出的梯度的值应该和样本m无关,所以给整个式子除于m:
\[\Lambda J = \begin{bmatrix}
\frac{\partial J}{\partial \theta _0} \\
\frac{\partial J}{\partial \theta _1} \\
\frac{\partial J}{\partial \theta _2} \\
... \\
\frac{\partial J}{\partial \theta _n}
\end{bmatrix} = \frac{2}{m}\begin{bmatrix}
\sum(X^{(i)}_b\theta - y^{(i)}) \\
\sum(X^{(i)}_b\theta - y^{(i)}) \cdot X_1^{(i)}\\
\sum(X^{(i)}_b\theta - y^{(i)}) \cdot X_2^{(i)}\\
...\\
\sum(X^{(i)}_b\theta - y^{(i)}) \cdot X_n^{(i)}
\end{bmatrix}\]
所以相应的目标函数应该为:
\[J = \frac{1}{m}\sum_{i=1}^{m}(y^{(i)} - \hat{y}^{(i)})^2 = \frac{1}{m}\sum_{i=1}^{m}(y^{(i)} - X_b\cdot \theta)^2
\]
此式子也是真实值和预测值之间的均方误差 $MSE(y,\hat y) $



