线性回归算法-4.多元线性回归算法

多元线性回归算法

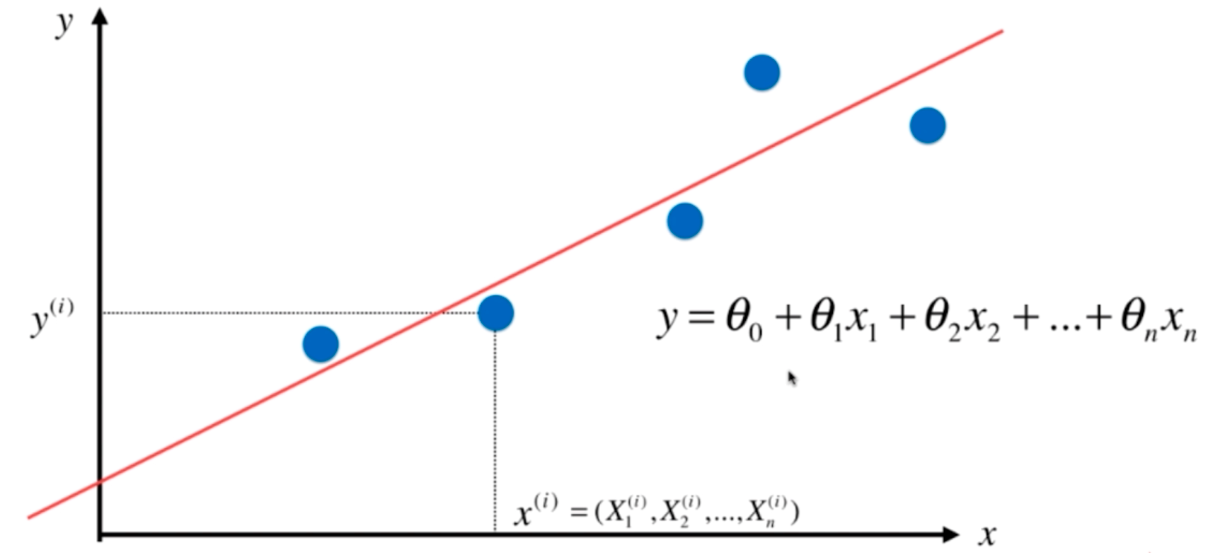
\(x^{(i)}\)由一个特征变为多个特征，此时拟合函数不是简单的\(y^{(i)} = ax^{(i)}+b\), 而是：
**$$\hat y^{(i)} = \theta _0x^{(i)}_0 + \theta _1x^{(i)}_1+ \theta _2x^{(i)}_2+...+\theta _{n}x^{(i)}_n，x_0\equiv 1 $$ **
注：上标i为第i个样本，下标1-n为样本i的多个特征值

由上式可得：

\[\theta = （\theta_0,\theta_1,\theta_2,\theta _0,...,\theta _n）^T \]

\[X^{(i)} = (X^{(i)}_0,X^{(i)}_1,X^{(i)}_2,...,X^{(i)}_n) \]

\[\hat y^{(i)} = X^{(i)}\cdot \theta \]

把上式推广到所有样本中：

\[ X_b = \begin{bmatrix} 1 & x^{(1)}_1 & x^{(1)}_2 & ... & x^{(1)}_n\\ 1 & x^{(2)}_1 & x^{(2)}_2 & ... & x^{(2)}_n\\ ... & & & & ...\\ 1 & x^{(m)}_1 & x^{(m)}_2 & ... & x^{(m)}_n \end{bmatrix}. \theta = \begin{bmatrix} \theta_0\\ \theta_1\\ \theta_2\\ ...\\ \theta_n\\ \end{bmatrix}\]

\[\hat y = X_b\cdot \theta \]

得到\(\theta\)的表达式（此推导过程较为复杂,感兴趣的话在网上找）：

\[\theta = (X^{T}_bX_b)^{-1}X^{T}_by \]

上式为多元线性回归的正规方程解（Normal Equation）
问题：时间复杂度较高，\(O(n^3)\)

多元线性回归的实现

封装LineRegression算法库

import numpy
from .metrics import r2_score

class LineRegression(object):
	"""docstring fos LineRegression"""
	def __init__(self):
		self.coef_ = None
		self.interception_ = None
		self._theta = None

	def fit_normal(self,X_train,y_train):

		assert X_train.shape[0] == y_train.shape[0],\
			"size of x_train must be equal to the size of y_train"

		X_b = numpy.hstack([numpy.ones((len(X_train),1)),X_train])
		self._theta = numpy.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)

		self.coef_ = self._theta[1:]    #系数
		self.interception_ = self._theta[0] #截距
		return self

	def predict(self,X_predict):

		assert self.coef_ is not None and self.interception_ is not None,\
			"must be fit before predict"
		assert X_predict.shape[1] == len(self.coef_),\
			"the feature number of X_predict must be equal X_train"

		X_b = numpy.hstack([numpy.ones((len(X_predict),1)),X_predict])
		y_predict = X_b.dot(self._theta)
		return y_predict

	def score(self,x_test,y_test):
		y_predict = self.predict(x_test)
		return r2_score(y_test,y_predict)


	def __repr__(self):
		return "LineRegression"

算法调用

import numpy
import matplotlib.pyplot as plt
from sklearn import datasets

# 加载波士顿房产数据集
boston = datasets.load_boston()
X = boston.data
y = boston.target

X = X[y<50]
y = y[y<50]

from mylib.model_selection import train_test_split
from mylib.LineRegression import LineRegression

X_train,X_test,y_train,y_test = train_test_split(X,y,seed=666)

reg = LineRegression()
reg.fit_normal(X_train,y_train)
# reg.predict(X_test)
reg.score(X_test,y_test)

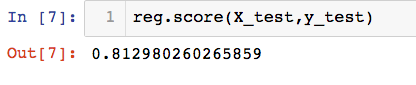
scikit-learn 中的LinearRegression

from sklearn.linear_model import LinearRegression
line_reg = LinearRegression()
line_reg.fit(X,y)