线性回归算法-1.简单线性回归原理
线性回归算法
- 解决回归问题
- 思想简单,实现容易
- 许多强大的非线性模型的基础
- 结果具有很好的解释性
- 蕴含机器学习中很多重要的思想
一类机器学习算法的思路:通过分析问题,找到问题的损失函数或者效用函数,通过最优化损失函数或者效用函数,确定机器学习的算法模型
简单线性回归的推导 - 最小二乘法
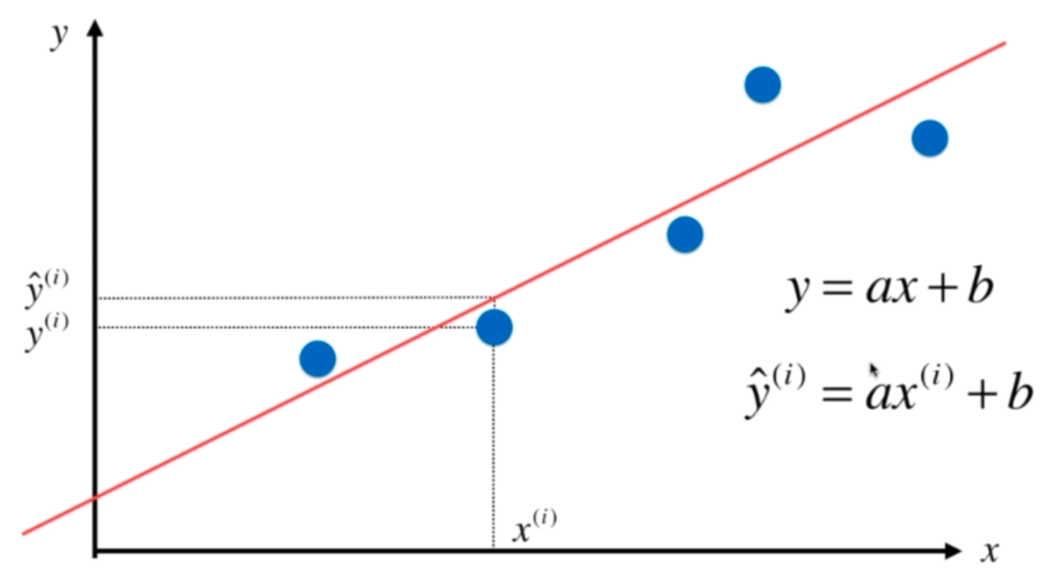
如图所示,对于样本,求一条拟合曲线:\(y=ax+b\)
\(\hat{y}^{(i)}\)为预测的某个样本\(x^{(i)}\)的预测值,而\(y^{(i)}\)为样本的真实值。
我们希望\(\hat{y}^{(i)}\)和\(y^{(i)}\)的差距尽量小:
\[(y^{(i)} - \hat{y}^{(i)})^2
\]
此处使用误差的平方而不使用误差的绝对值是因为绝对值函数不是处处可导的,而误差平方也无形之中放大了最大的误差,有利于更好的衡量算法
考虑所有的样本:
\[\sum_{i=1}^{m}({y}^{(i)} - \hat{y}^{(i)})^2
\]
把 \(\hat{y}^{(i)}=ax^{(i)}+b\) 代入上式:

具体求解过程
\[J(a,b) = \sum_{i=1}^{m}({y}^{(i)} - ax^{(i)}-b)^2
\]
对b求偏导数:
\[\frac{\partial J(a,b)}{\partial b} = \sum_{i=1}^{m}2({y}^{(i)} - ax^{(i)}-b)(-1) = 0
\]
\[\sum_{i=1}^{m}({y}^{(i)} - ax^{(i)}-b) = 0
\]
\[\sum_{i=1}^{m}{y}^{(i)} - a\sum_{i=1}^{m}x^{(i)}-\sum_{i=1}^{m}b = 0
\]
\[\sum_{i=1}^{m}{y}^{(i)} - a\sum_{i=1}^{m}x^{(i)}-mb = 0
\]
\[mb = \sum_{i=1}^{m}{y}^{(i)} - a\sum_{i=1}^{m}x^{(i)}
\]
\[b = \overline{y} -a\overline{x}
\]
对a求偏导数:
\[\frac{\partial J(a,b)}{\partial a} = \sum_{i=1}^{m}2({y}^{(i)} - ax^{(i)}-b)(-x^{(i)}) = 0
\]
\[\sum_{i=1}^{m}({y}^{(i)} - ax^{(i)}-b)(x^{(i)}) = 0
\]
\[\sum_{i=1}^{m}({y}^{(i)} - ax^{(i)}-b)(x^{(i)}) = 0
\]
代入 \(b = \overline{y} -a\overline{x}\)
\[\sum_{i=1}^{m}({y}^{(i)} - ax^{(i)}-\overline{y} +a\overline{x})(x^{(i)}) = 0
\]
\[\sum_{i=1}^{m}(x^{(i)}{y}^{(i)} - a(x^{(i)})^2-x^{(i)}\overline{y} +a\overline{x}x^{(i)}) = 0
\]
\[\sum_{i=1}^{m}(x^{(i)}{y}^{(i)}-x^{(i)}\overline{y}) - \sum_{i=1}^{m}(a(x^{(i)})^2 -a\overline{x}x^{(i)}) = 0
\]
提出a:
\[a = \frac{\sum_{i=1}^{m}(x^{(i)}{y}^{(i)}-x^{(i)}\overline{y})}{\sum_{i=1}^{m}((x^{(i)})^2 -\overline{x}x^{(i)})}
\]
根据:
\[{\sum_{i=1}^{m}x^{(i)}\overline{y}} = \overline{y}{\sum_{i=1}^{m}x^{(i)}} = m\overline{y} \overline{x}= \overline{x}{\sum_{i=1}^{m}y^{(i)}} = {\sum_{i=1}^{m}\overline{x}y^{(i)}}
\]
化简上式,最终得:
\[a =\frac{\sum_{i=1}^{m}(x^{(i)} -\overline{x})(y^{(i)} -\overline{y})}{\sum_{i=1}^{m}(x^{(i)} -\overline{x})^2}
\]



