精准用户画像！商城用户分群2.0！⛵

💡 作者：韩信子@ShowMeAI
📘 数据分析实战系列：https://www.showmeai.tech/tutorials/40
📘 机器学习实战系列：https://www.showmeai.tech/tutorials/41
📘 本文地址：https://www.showmeai.tech/article-detail/334
📢 声明：版权所有，转载请联系平台与作者并注明出处
📢 收藏ShowMeAI查看更多精彩内容

很多公司的技术人员在做用户画像的工作，细分客户/客户分群是一个很有意义的工作，可以确保企业构建更个性化的消费者针对策略，同时优化产品和服务。

在机器学习的角度看，客户分群通常会采用无监督学习的算法完成。应用这些方法，我们会先收集整理客户的基本信息，例如地区、性别、年龄、偏好等，再对其进行分群。

在之前的文章 📘基于机器学习的用户价值数据挖掘与客户分群中，ShowMeAI 已经做了一些用户分群实操介绍，本篇内容中，ShowMeAI 将更深入地介绍聚类分群的方法，使用更丰富的建模方式，并剖析模型评估的方法模式。

💡 数据加载 & 基本处理

我们先使用 pandas 加载 🏆Mall_Customers数据，并做了一些最基本的数据清洗，把字段名称更改为清晰可理解的字符串格式。

🏆 实战数据集下载（百度网盘）：公众号『ShowMeAI研究中心』回复『实战』，或者点击 这里 获取本文 [27]基于多种聚类算法的商城用户分群！绘制精准用户画像 『Mall_Customers数据集』

⭐ ShowMeAI官方GitHub：https://github.com/ShowMeAI-Hub

df= pd.read csv( "Mall Customers.csv")
df.rename (columns={"CustomerID": "id", "Age": "age", "Annual Income (k$)": "annual_income", "Spending Score (1-100)": "spending_score"}, inplace=True)
df.drop(columns=["id"], inplace=True)

💡 探索性数据分析

本文数据操作处理与分析涉及的工具和技能，欢迎大家查阅 ShowMeAI 对应的教程和工具速查表，快学快用。

下面我们对数据做一些探索性数据分析，首先我们的特征字段可以分为数值型和类别型两种类型。后面我们单独对两类特征字段进行分析。

numcol = ["age", "annual_income", "spending_score"]
objcol = ['Gender']

💦 单变量分析

① 类别型特征

我们对性别（女性和男性）做计数统计和绘图，代码如下：

sns.set_style("ticks")
my_pal = {"Male": "slateblue", "Female": "lightsalmon"}
ax = sns.countplot(data=df, x="Gender", palette=-my_pal)
ax.grid(True, axis='both' )
for p in ax.patches:
        ax.annotate( '{:.Of}'. format(p.get _height()), (p.get _x()+0.25, p.get_height()+0.3))
        percentage = "{:.If}%'. format(100 * p.get height )/lendf[ "Gender" ]))
        ax.annotate(percentage, (p.get x()+0.25, p.get height ( )/2))
olt.title( "Gender Countolot")

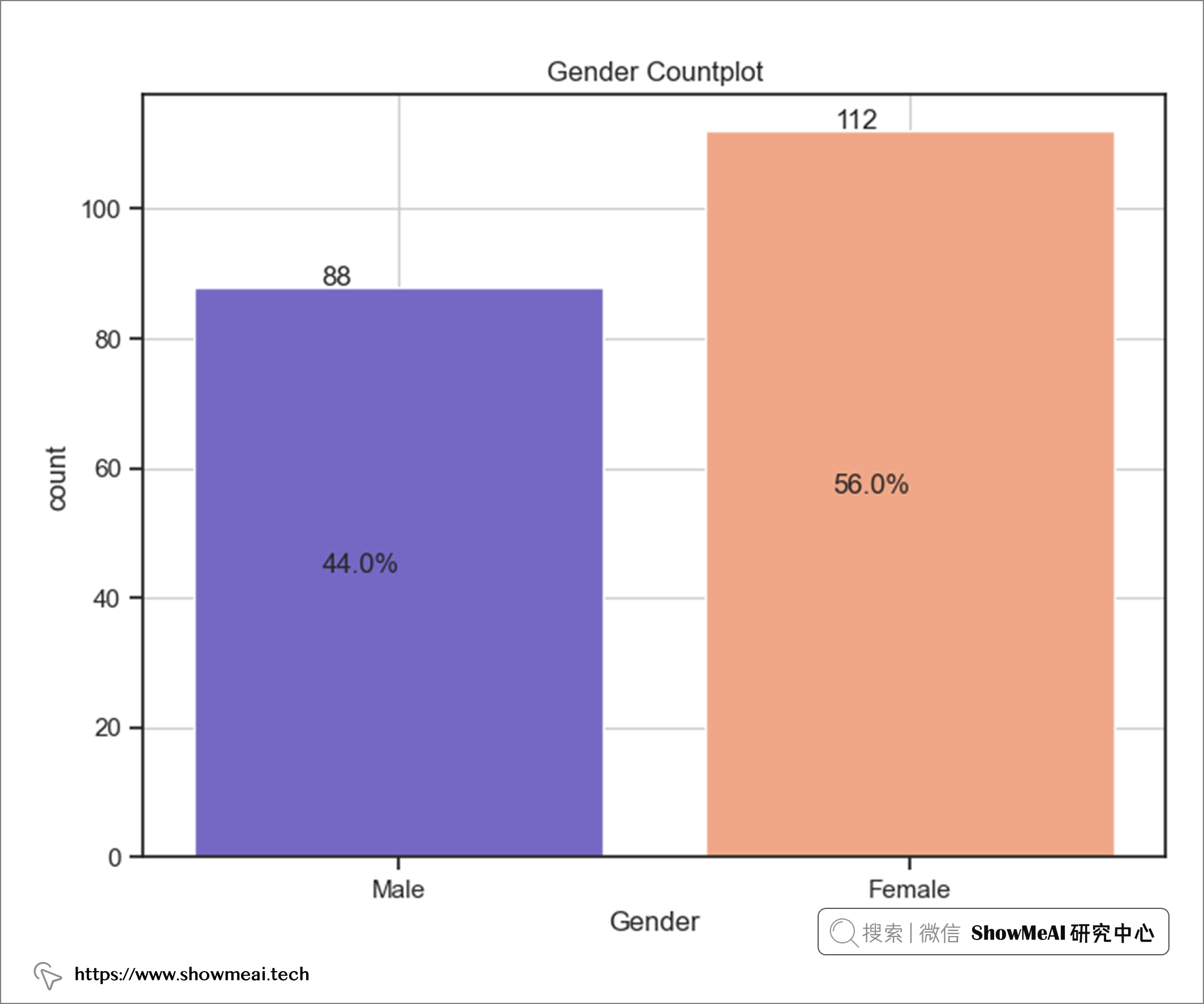
② 数值特征

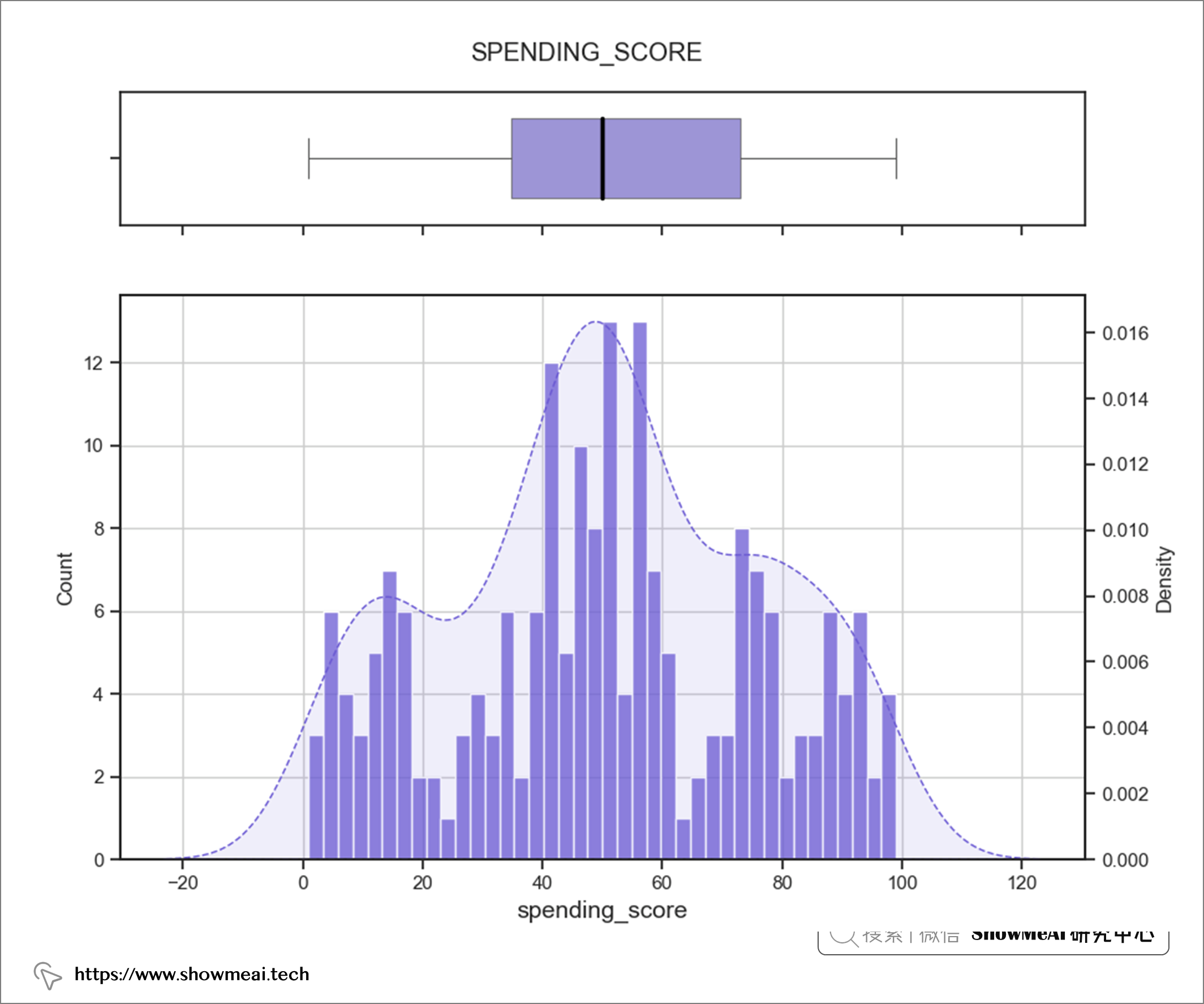
后续的用户分群会使用到聚类算法，为了确保聚类算法可以正常工作，我们会查看连续值数据分布并检查异常值。如果不加这个步骤，严重倾斜的数据和异常值可能会导致很多问题。

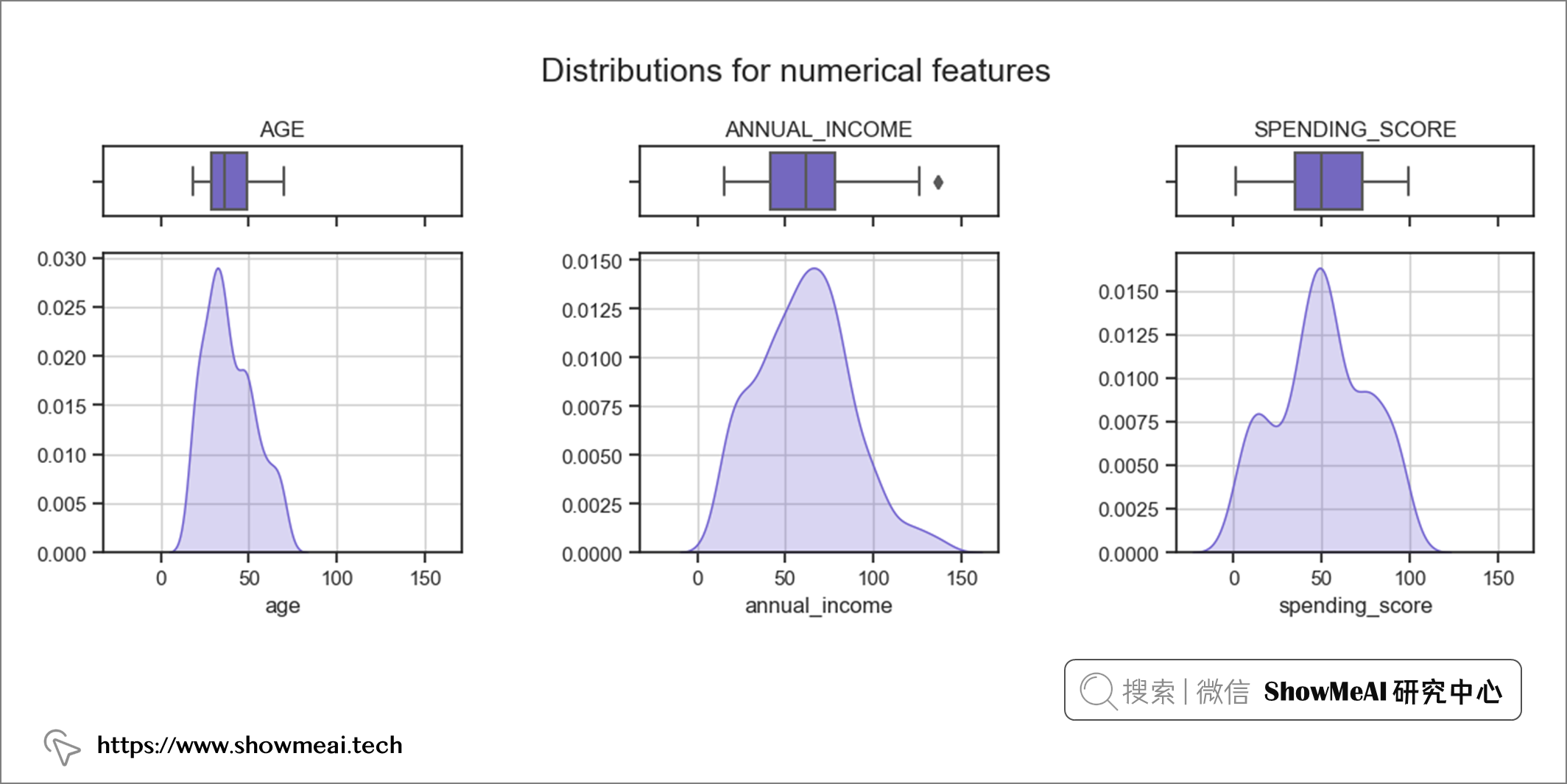
如上图所示，除了annual_income特征有一个异常值之外，大多数数值特征已经很规整了。

sns.set_style("ticks", {'axes.grid' : False})
for idx, col in enumerate (numcol):
        plt.figure()
        f, ax = plt.subplots(nrows=2, sharex=True, gridspec_kw={"height_ratios": (0.2,0.85)}, figsize=(10,8));
        plt.suptitle(f"{col.upper()}",y=0.93);
        sns.boxplot(data=df,x=col,ax=ax[0],color="slateblue",boxprops=dict(alpha=.7),
                                linewidth=0.8, width=0.6, fliersize=10,
                                flierprops={ "marker" :"O", "markerfacecolor": "slateblue"},
                                medianprops={ "color": "black", "linewidth":2.5})

        sns.histplot(data=df, ×=col, ax=ax[1],multiple="layer", fill=True, color= "slateblue", bins=40)
        ax2 =ax[1].twinx()
        sns.kdeplot(data=df, x=col, ax=ax2,
                                multiple="layer",
                                fill=True,
                                color="slateblue",
                                bw_adjust=0.9,
                                alpha=0.1,
                                linestyles="--")

        ax[1].grid(False)
        ax[0].set(xlabel="");

        ax[1].set _xlabel(col, fontsize=14)
        ax[1].grid(True)

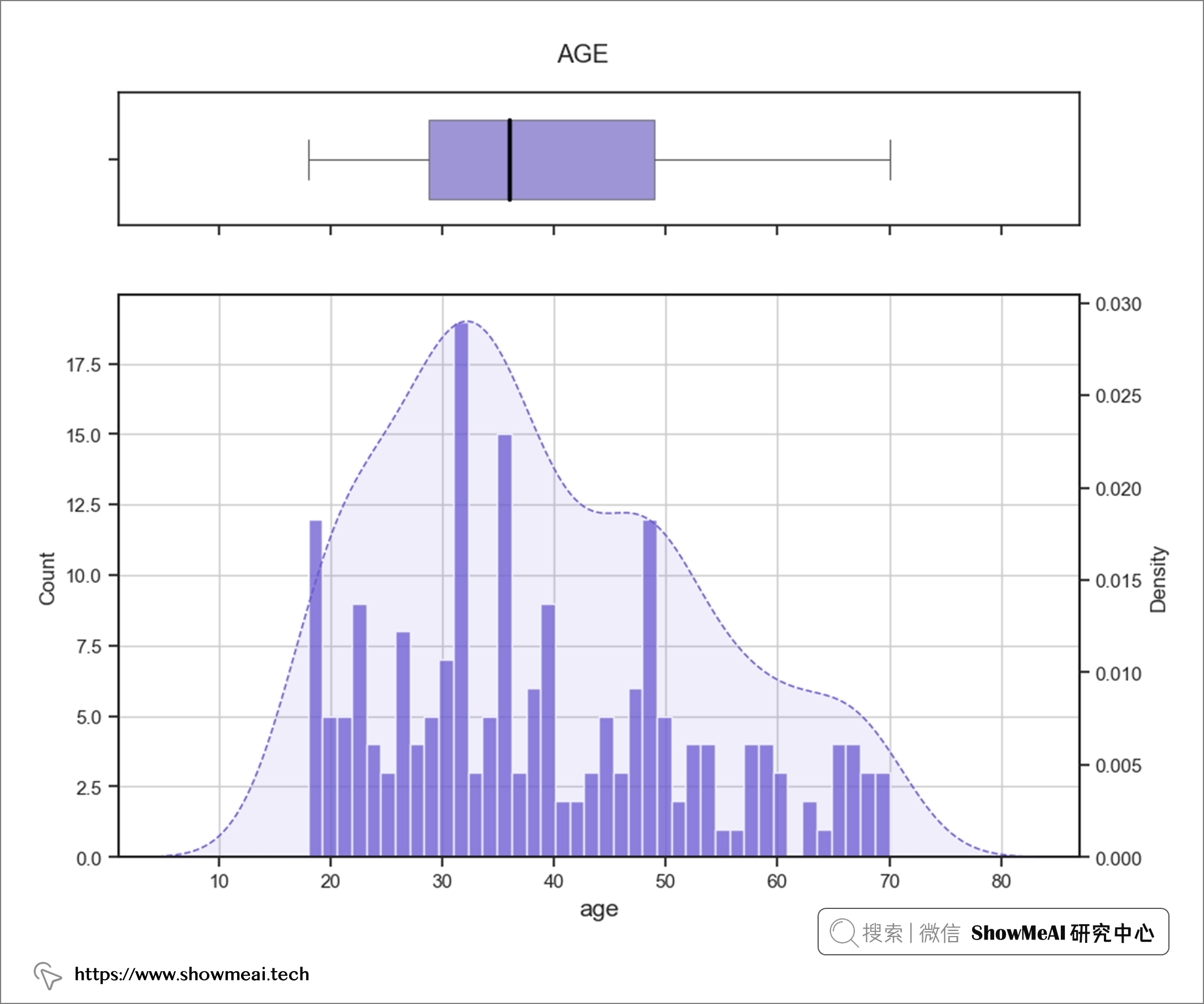
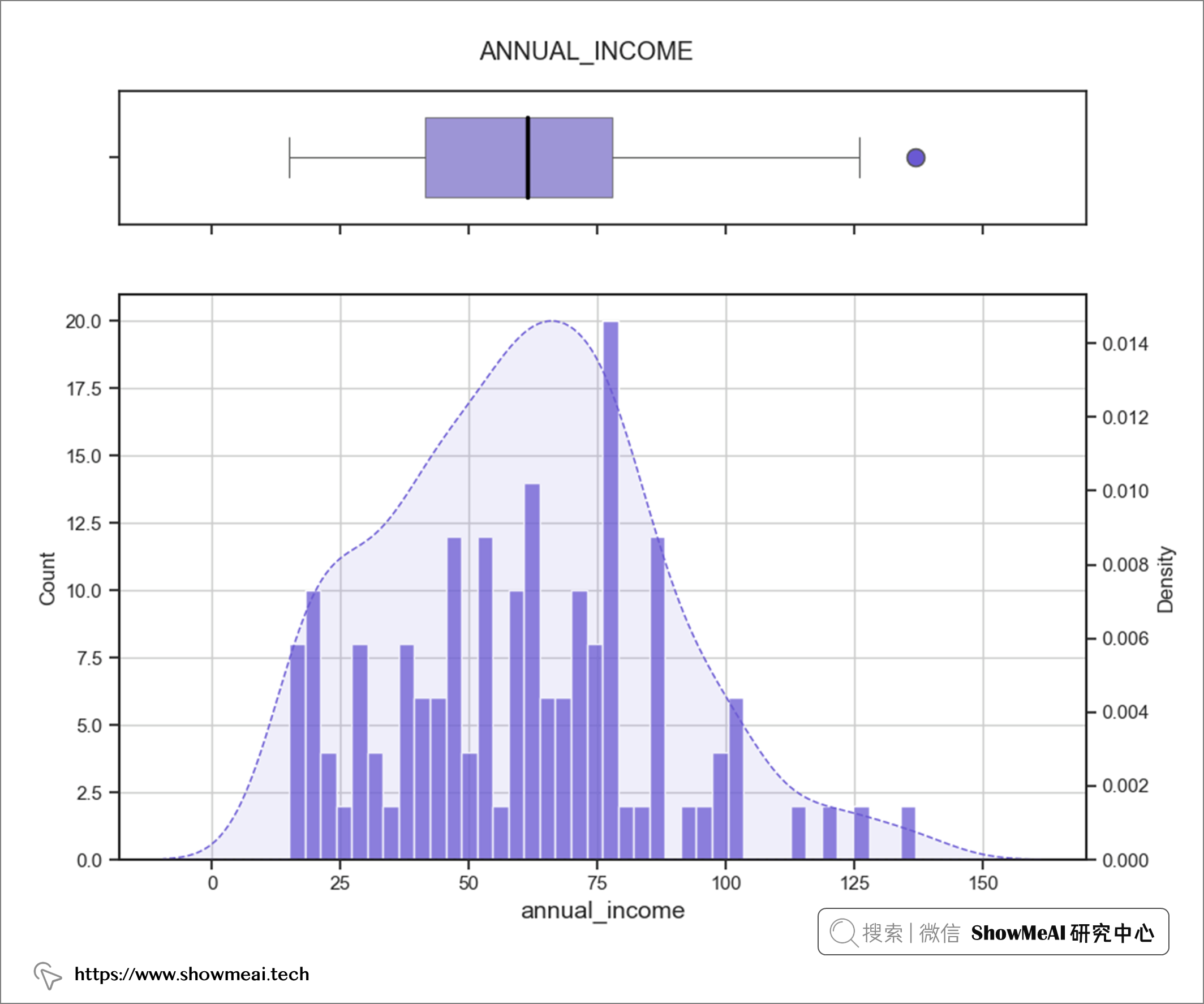
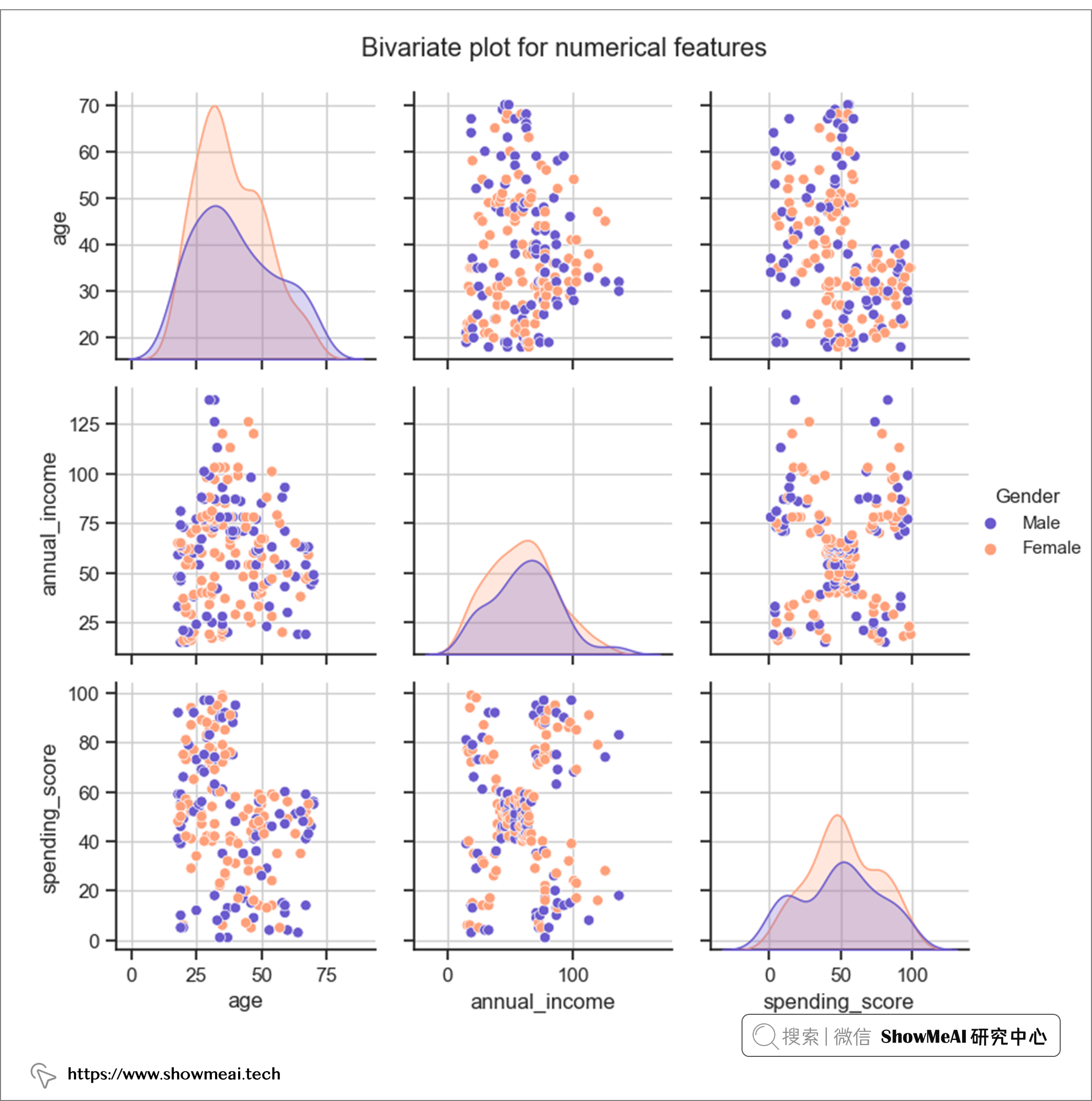
💦 双变量分析

我们再对两两的特征做联合分析，代码和绘制结果如下：

sns.set_style("ticks", {'axes.grid' : False})

def pairplot_hue(df, hue, **kwargs):
    g = sns.pairplot(df, hue=hue, **kwargs)
    g.fig.subplots_adjust(top=0.9)
    g.fig.suptitle(hue)
    return g

pairplot_hue(df[numcol+objcol], hue='Gender')

💡 建模

💦 数据缩放

为了保证后续聚类算法的性能效果，数值特征在送入模型之前需要做缩放处理。我们直接使用 sklearn 中的 MinMaxScaler 缩放方法来完成这项工作，将数值型字段数据范围转换为 [0,1]。

scaler = MinMaxScaler()
df_scaled = df.copy()
for col in numcol:
        df scaled[col] = pd.DataFrame(scaler.fit_transform(df_scaled[col].values.reshape(-1,1) ))

💦 模型选择

本篇内容涉及的聚类无监督学习算法，欢迎大家查看ShowMeAI的教程文章：

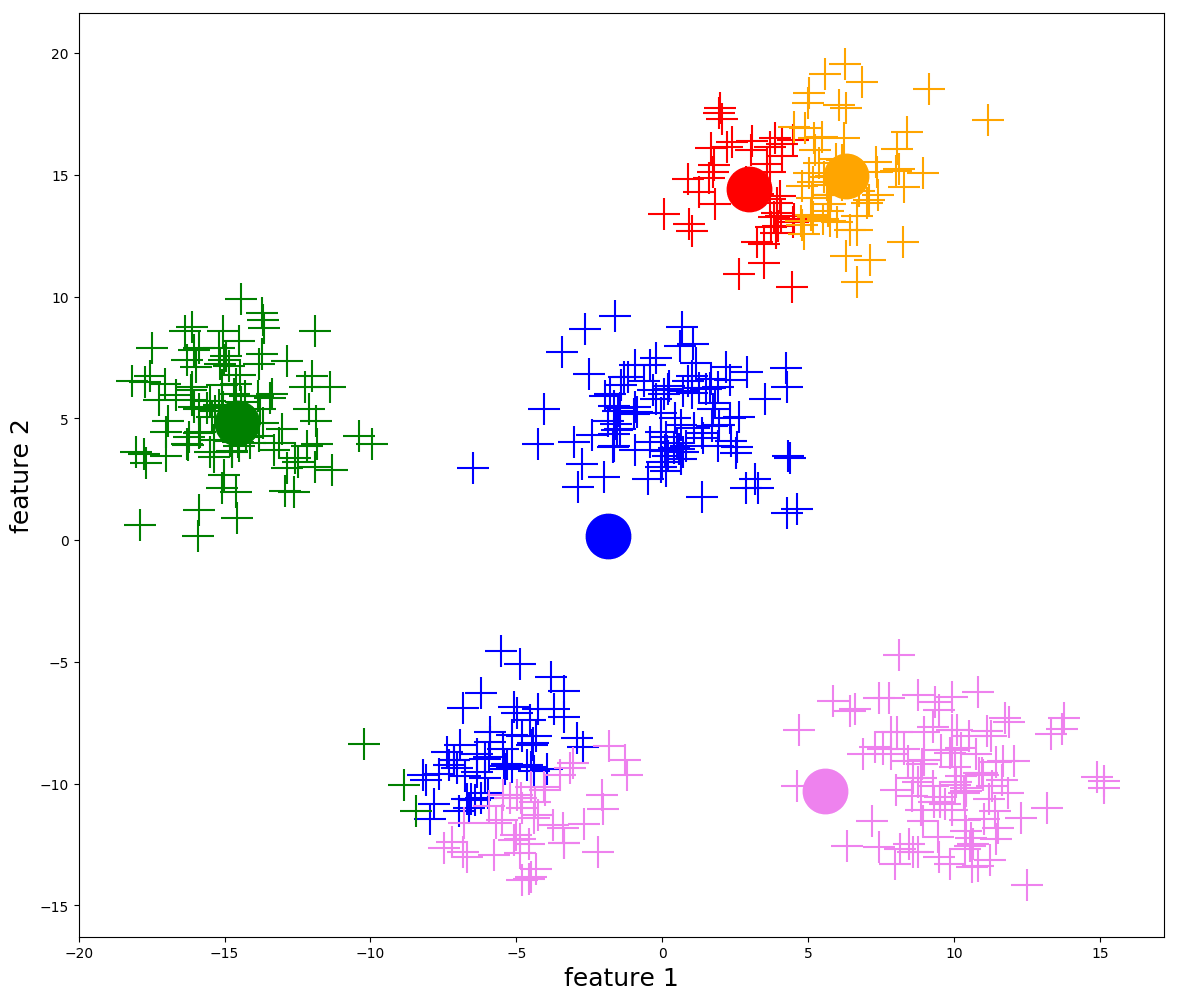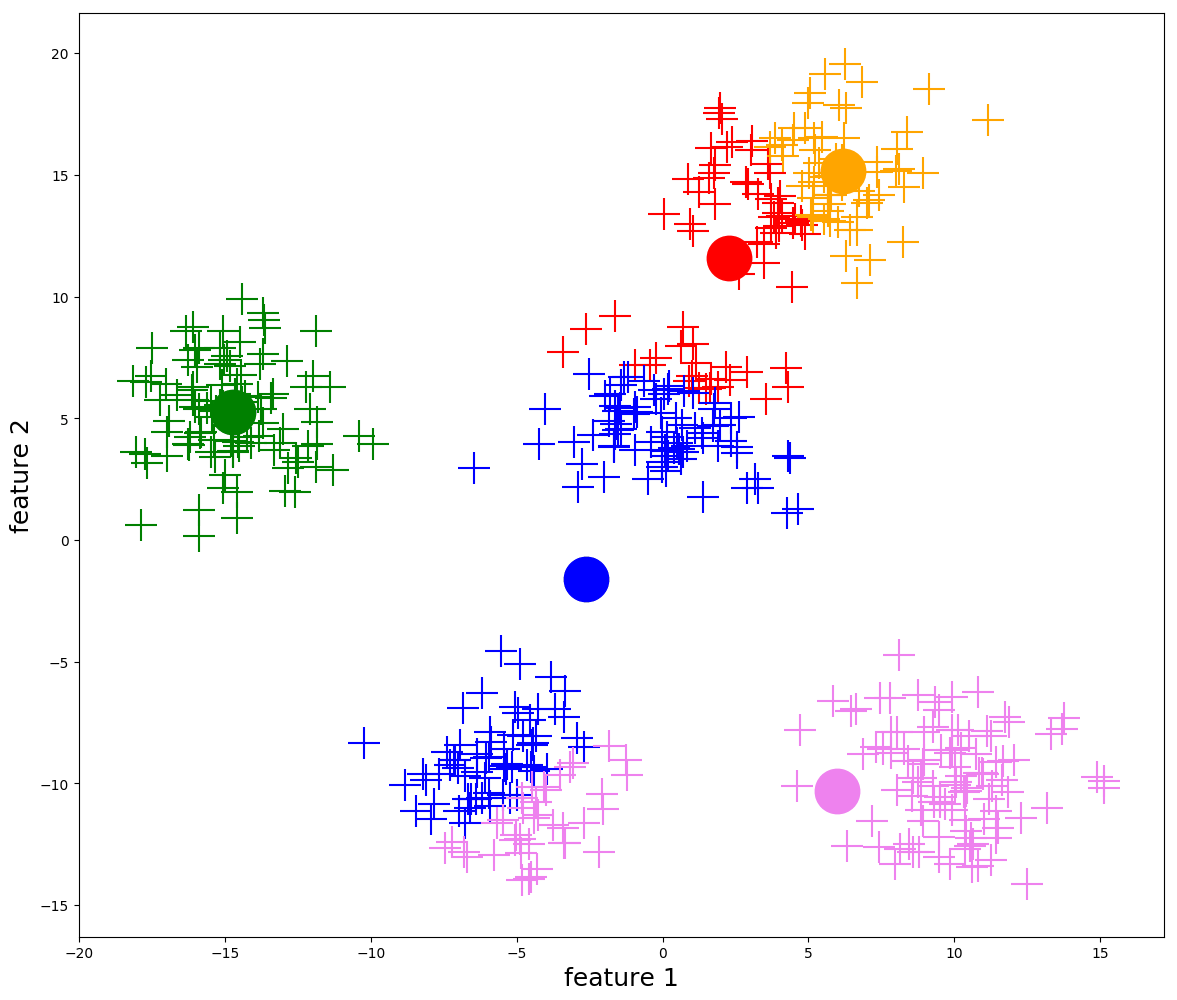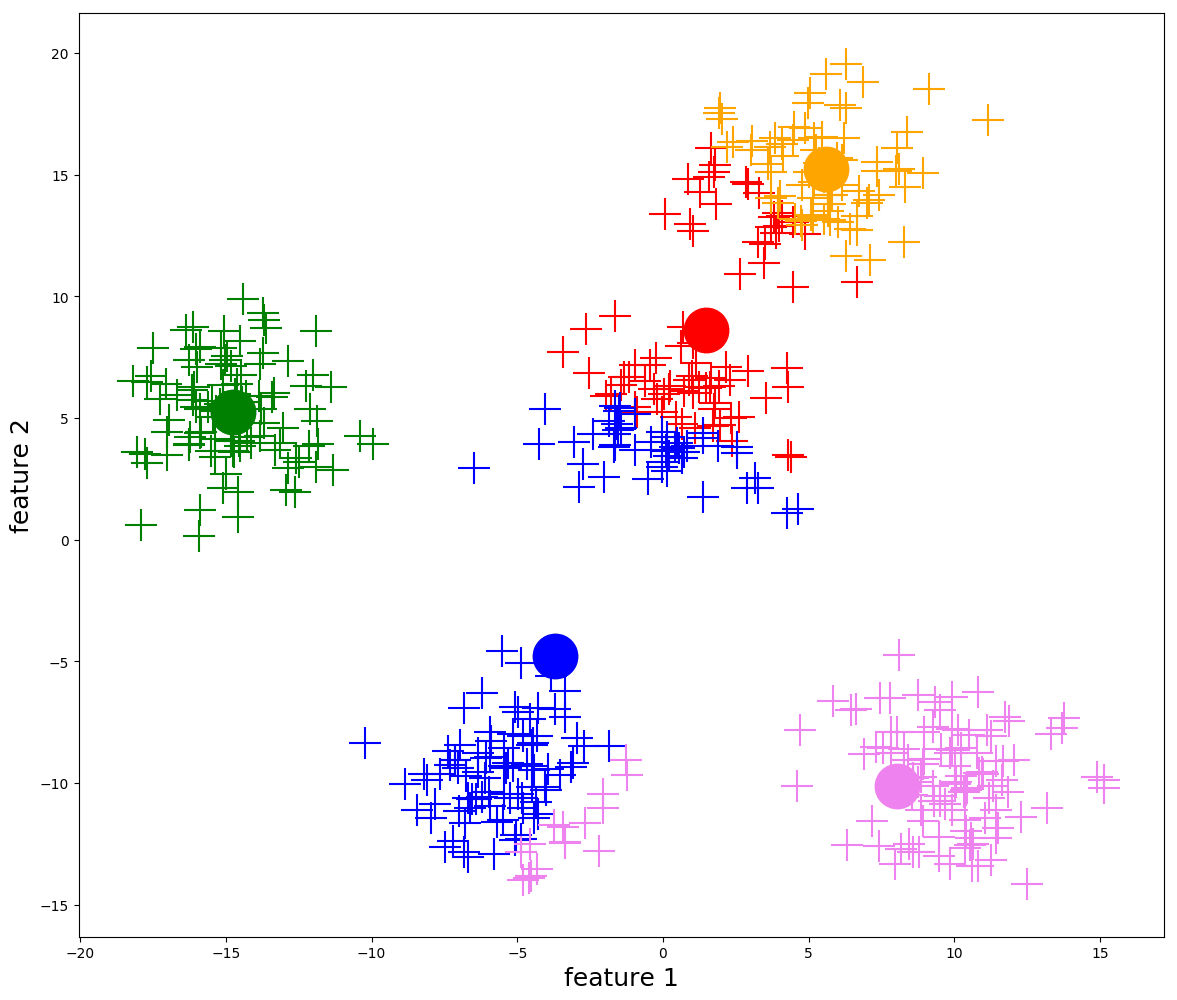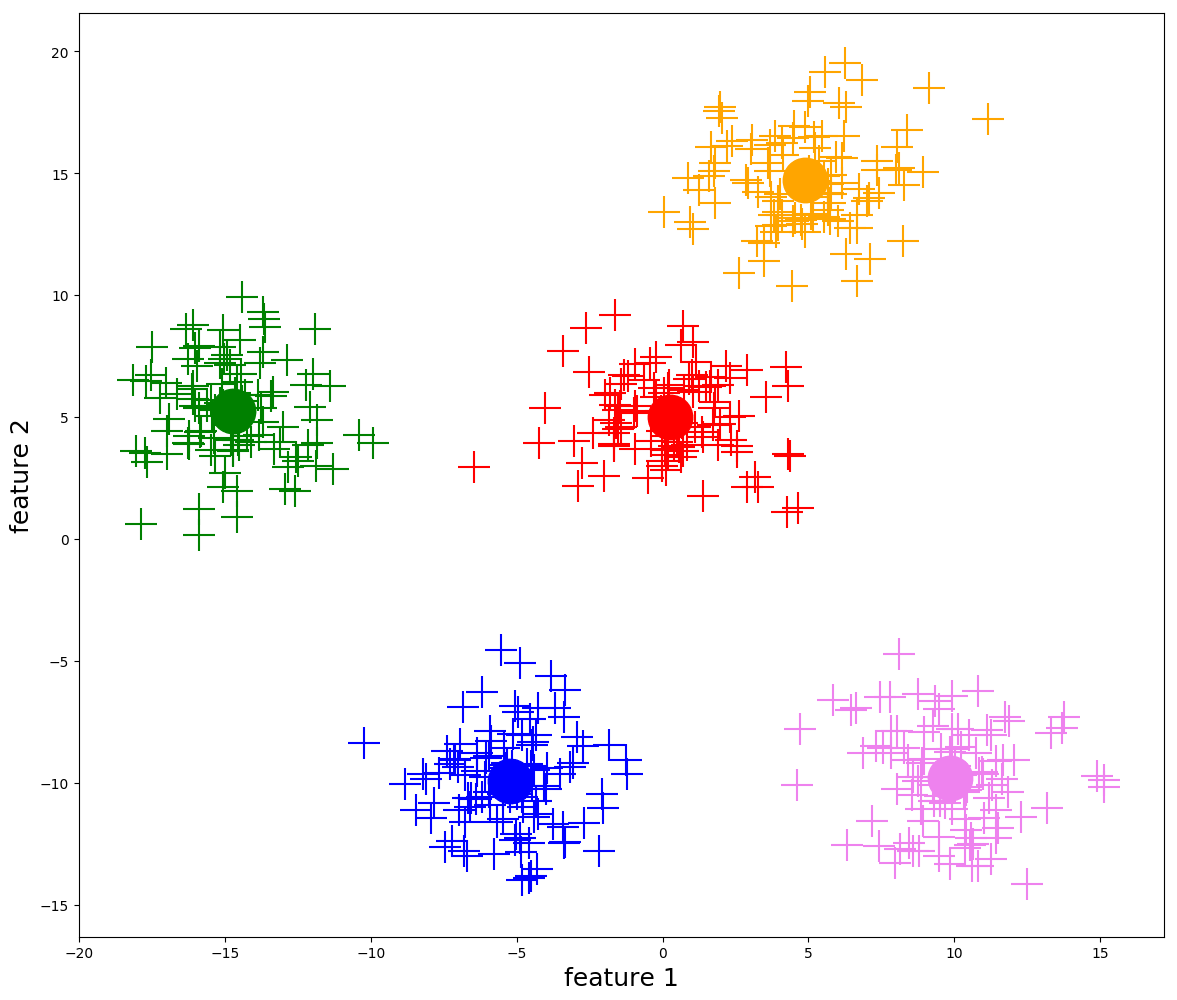
① K-Means 聚类

K-Means 算法是一种无监督学习算法，它通过迭代和聚合来根据数据分布确定数据属于哪个簇。

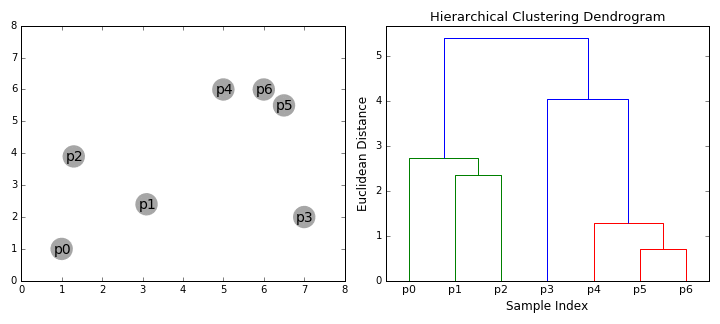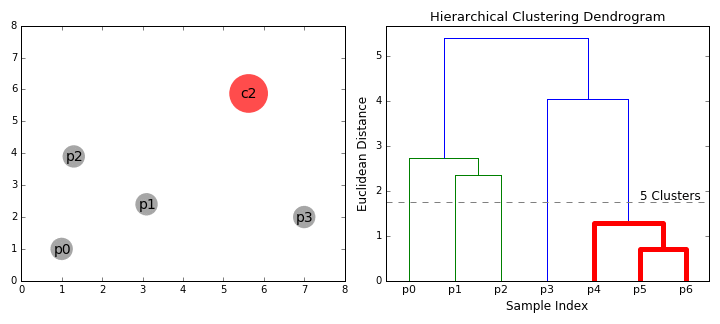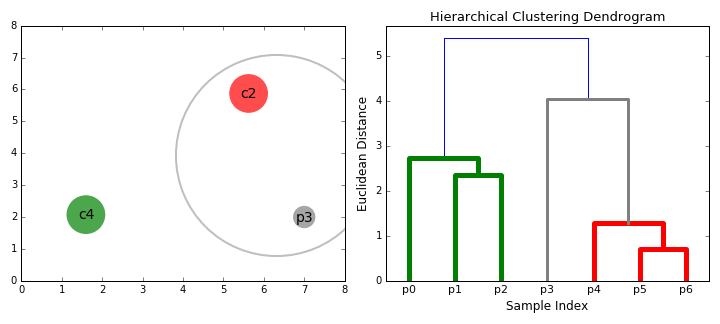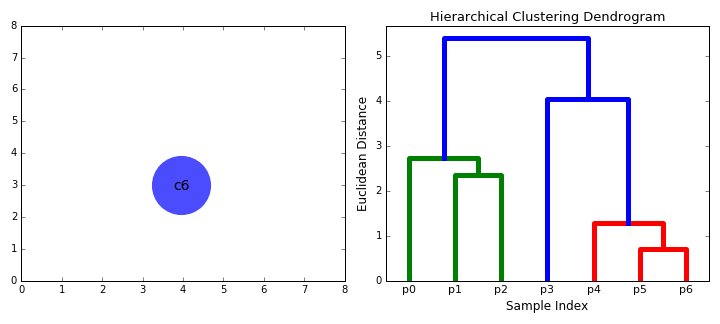
② 层次聚类(BIRCH) 算法

BIRCH（Balanced Iterative Reducing and Clustering Using Hierarchies）翻译为中文就是『利用层次方法的平衡迭代规约和聚类』，全称非常复杂。简单来说，BIRCH 算法利用了一个树结构来帮助我们快速的聚类，这个特殊的树结构，就是我们后面要详细介绍的聚类特征树（CF-tree）。简单地说算法可以分为两步：

  • 1）扫描数据库，建立一棵存放于内存的 CF-Tree，它可以被看作数据的多层压缩，试图保留数据的内在聚类结构；

  • 2）采用某个选定的聚类算法，如 K-Means 或者凝聚算法，对 CF 树的叶节点进行聚类，把稀疏的簇当作离群点删除，而把更稠密的簇合并为更大的簇。

💦 模型评估

① 聚类算法评估

虽然说聚类是一个无监督学习算法，但我们也有一些方法可以对其最终聚类效果进行评估，对我们的建模和聚合有一些指导作用。

◉ 轮廓分数（Silhouette score）

轮廓分数（ Silhouette score）是一种常用的聚类评估方式。对于单个样本，设 a 是与它同类别中其他样本的平均距离，b 是与它距离最近不同类别中样本的平均距离，轮廓系数为：

对于一个数据集，它的轮廓系数是所有样本轮廓系数的平均值。轮廓系数取值范围是 [-1,1]，同类别样本越距离相近且不同类别样本距离越远，分数越高。

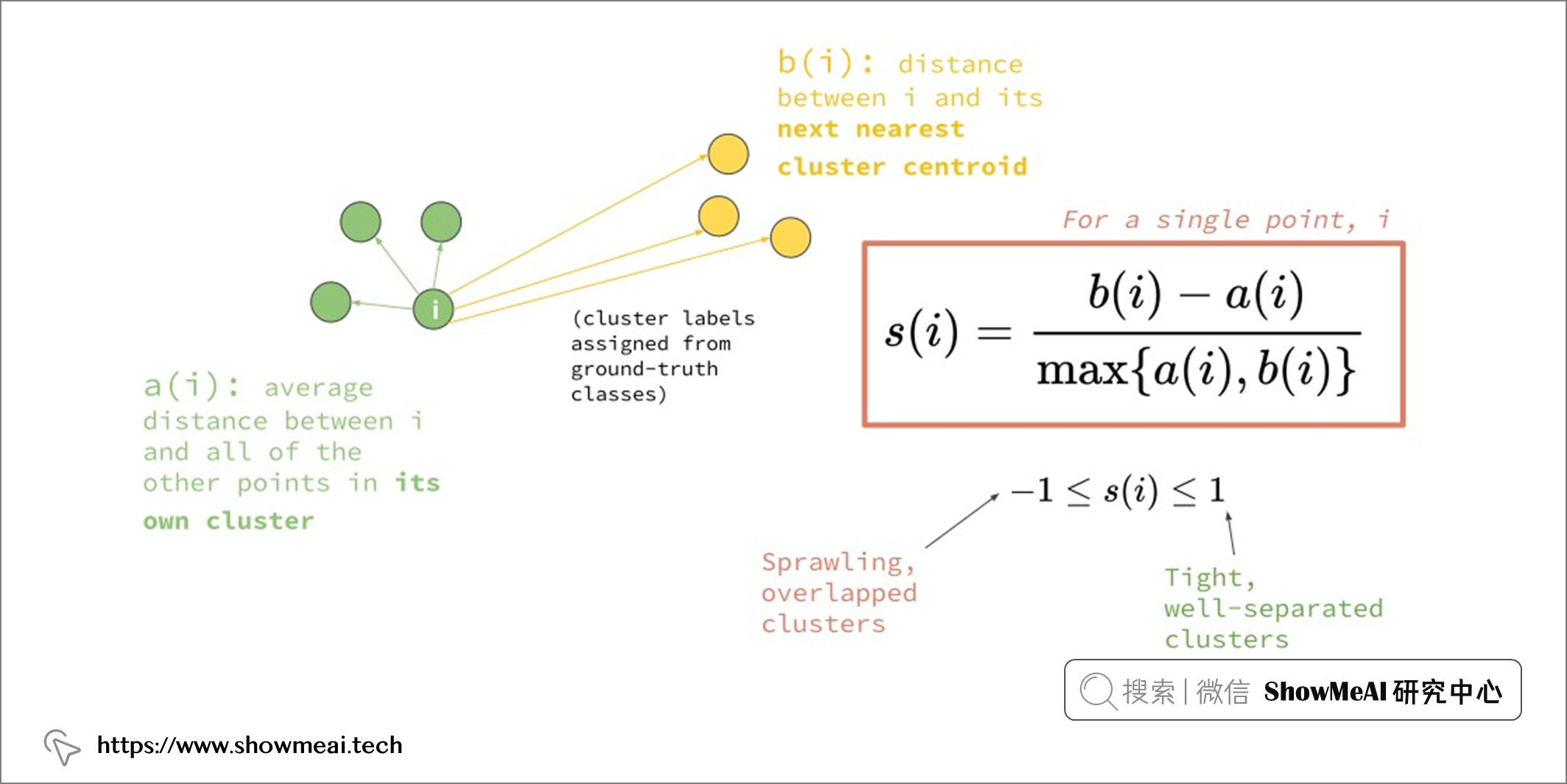
◉ 卡林斯基哈拉巴斯得分（Calinski Harabasz score）

卡林斯基哈拉巴斯得分（Calinski Harabasz score）也称为方差比标准，由所有簇的簇间离散度（Between Group Sum of Squares, BGSS）之和与簇内离散度（Within Group Sum of Squares, WGSS）之和的比值计算得出。较高的 Calinski Harabasz 分数意味着更好的聚类（每个聚类中更密集）。以下给出计算过程：

第一步：计算簇间离散度（Between Group Sum of Squares, BGSS）

第二部：计算簇内离散度（Within Group Sum of Squares, WGSS）

第三步：计算卡林斯基哈拉巴斯得分（Calinski Harabasz score）

◉ 戴维斯布尔丹得分（Davies Bouldin score）

戴维斯布尔丹得分（Davies Bouldin score）表示每个集群与与其最相似的集群或每个集群的内部模式的平均相似度。最低可能或最接近零表示更好的聚类。

② 应用 K-Means 聚类

我们先应用 K-Means 聚类对数据进行建模，聚合得到不同的用户簇，代码如下：

k_range = range(2,10)
for x in k range:
        model = KMeans(n_clusters=x, random_state=42)
  X = df_scaled[[ "annual_ income", "spending_score"]]
  model.fit(x)

评估 K-Means 算法的一种非常有效的方法是肘点法，它会可视化具有不同数量的簇的平方距离之和（失真分数）的加速变化（递减收益）的过程。

我们结合上述提到的3个得分，以及肘点法进行计算和绘图如下：

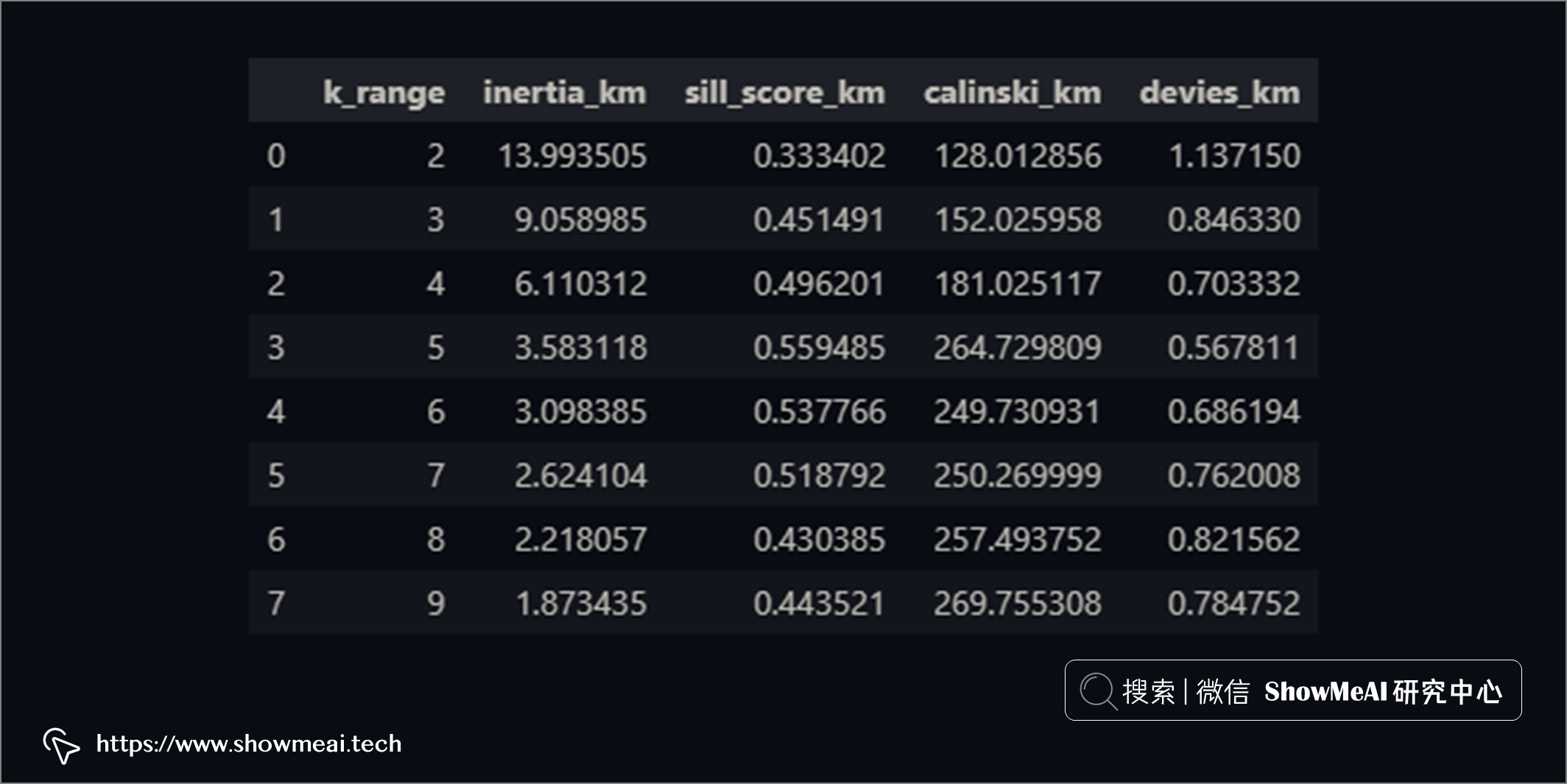
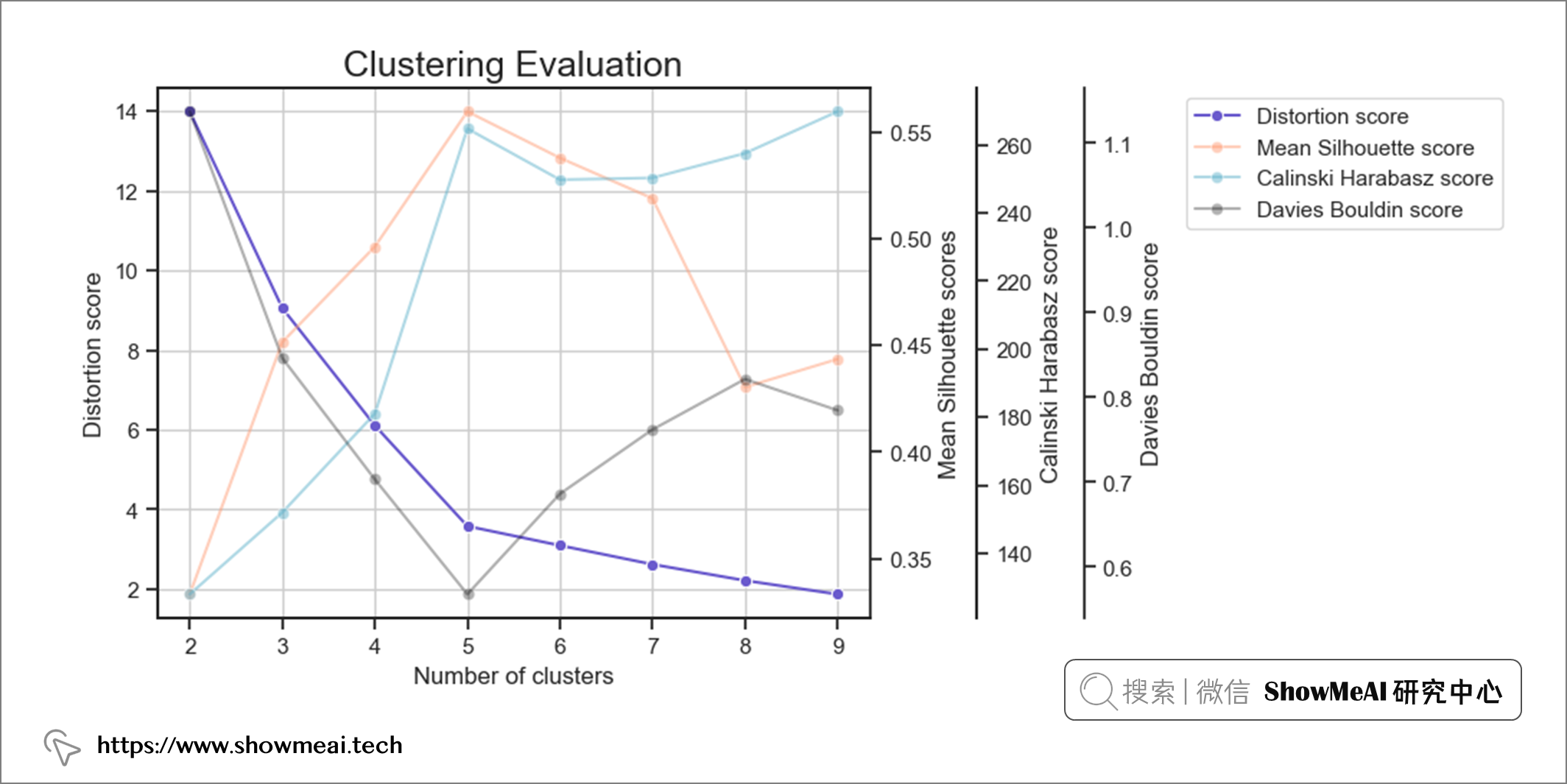
如上图所示，簇数 = 5 是适用于该数据集的适当簇数，因为它有着这些特性：

  • 开始递减收益（肘法）
  • 最高平均轮廓分数
  • 相对较高的 Calinski Harabarsz 评分（局部最大值）
  • Davies Bouldin 最低分数

我们以5为聚类个数，对数据重新聚类，并分发聚类 id，然后再对数据进行分布分析绘图，不同的用户簇的数据分布如下（我们可以比较清晰看到不同用户群的分布差异）。

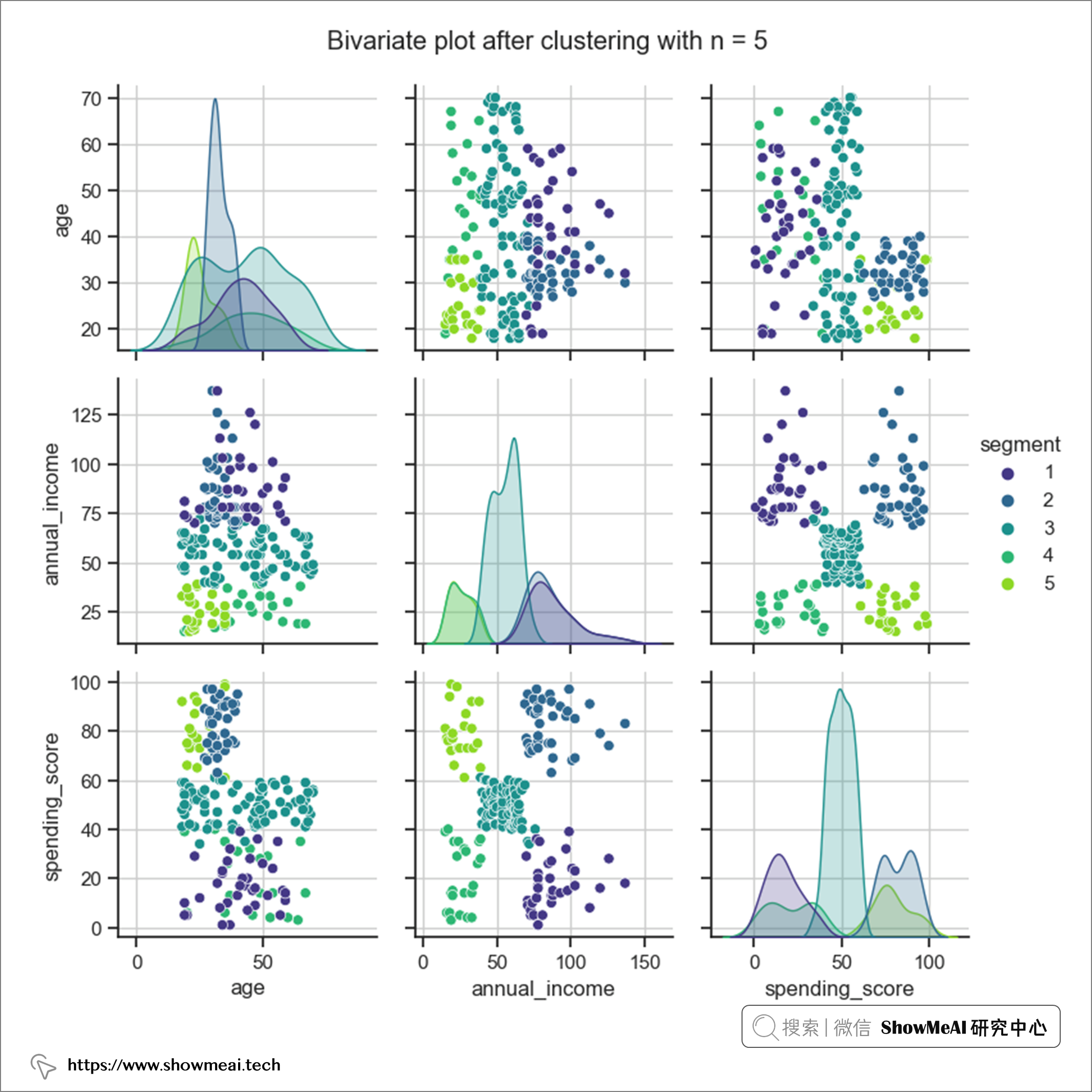
③ 应用 BIRCH 聚类

我们再使用 BIRCH 进行聚类，代码如下：

n = range(2,10)
for x in n:
  model = Birch(n_clusters=x, threshold=0.17)
  X = df_scaledI[ "annual income", "spending_score"]]
  model.fit(X)

与 K-Means 聚类不同，BIRCH 聚类没有失真分数。其他3 个评分指标（Silhouette、CH、DBI）仍然相同。

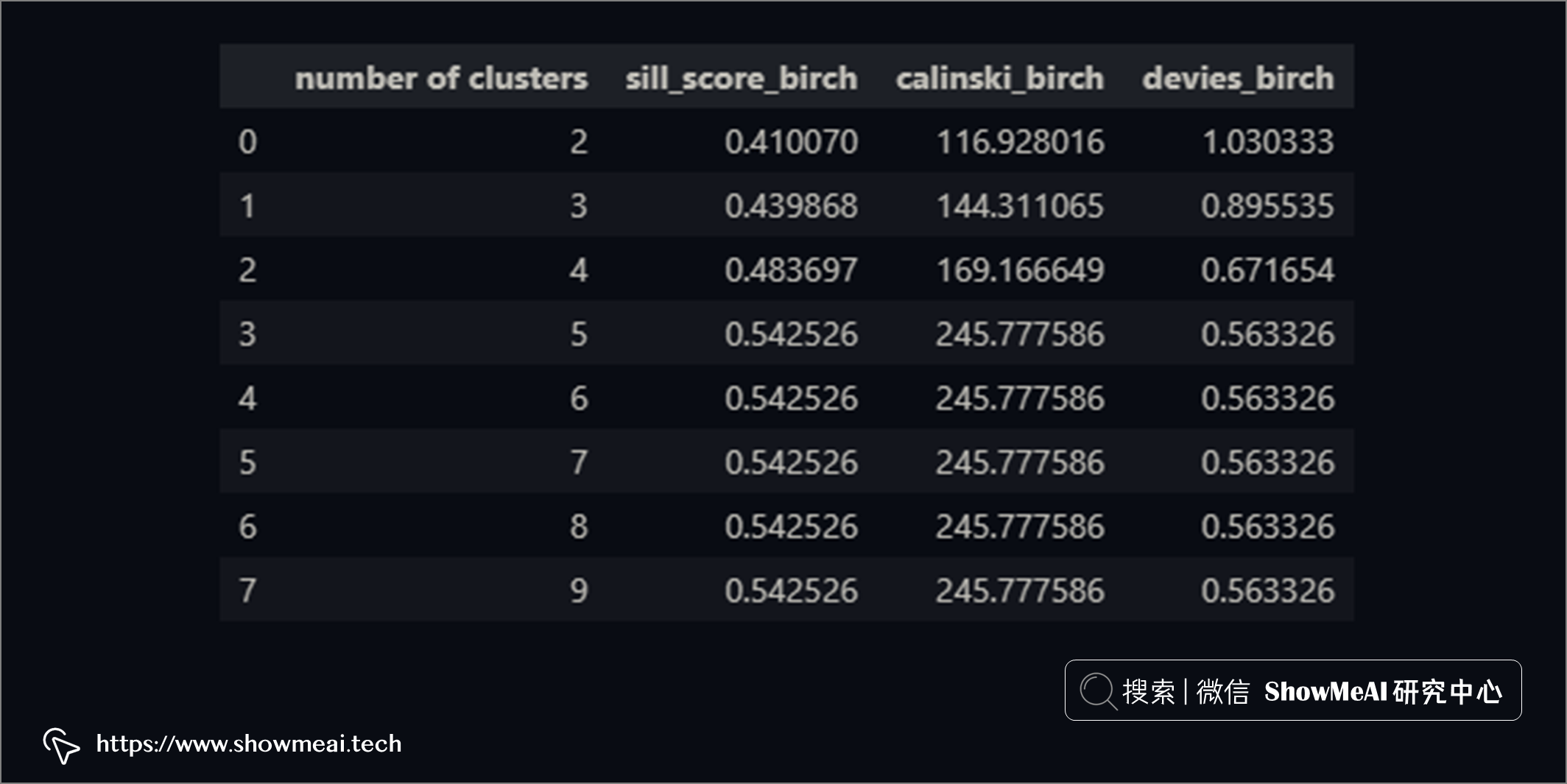
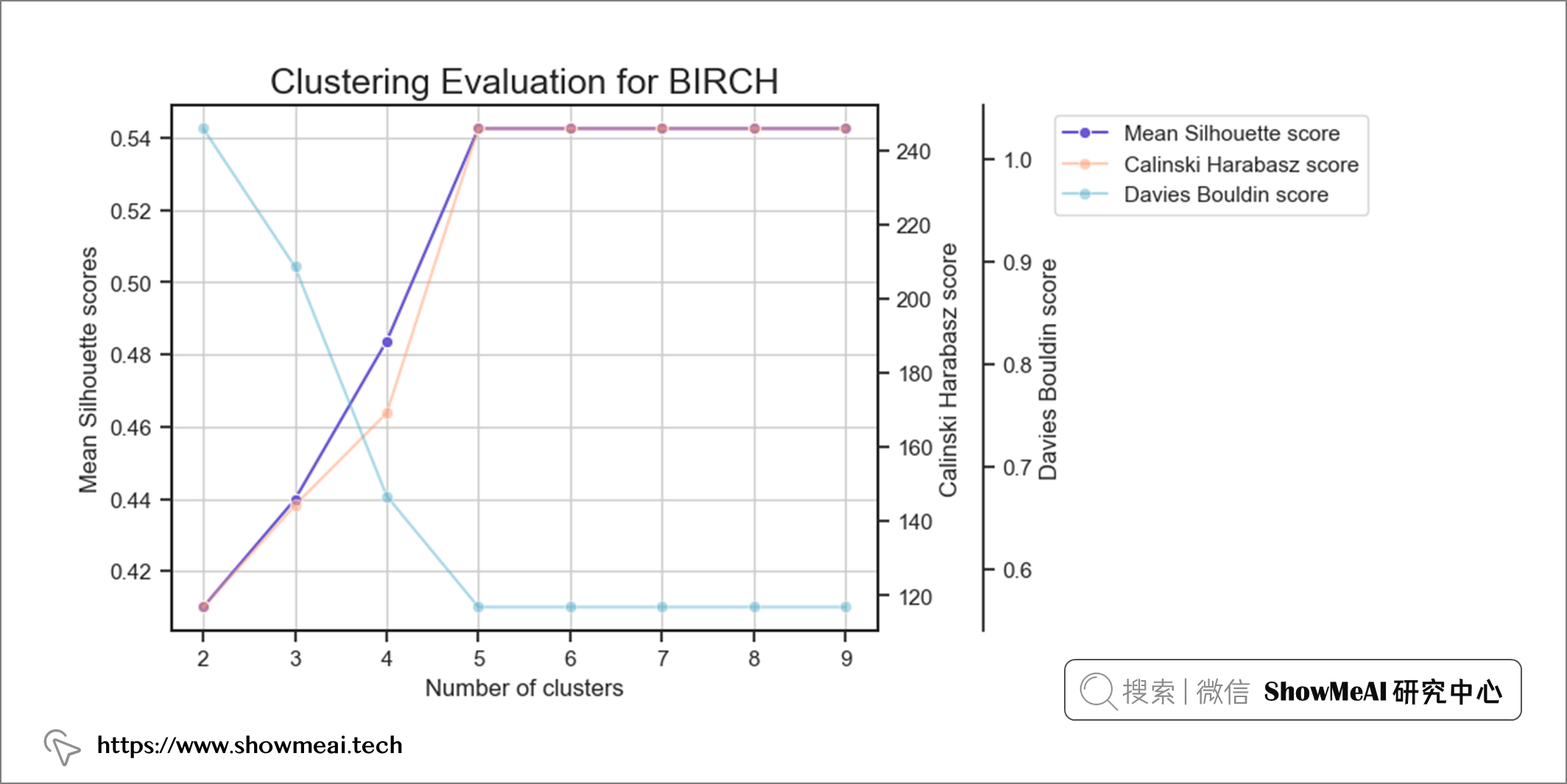
BIRCH 的计算也给出了簇数等于5这样的一个结论。我们同样对数据进行分布分析绘图，不同的用户簇的数据分布如下（依旧可以比较清晰看到不同用户群的分布差异）。

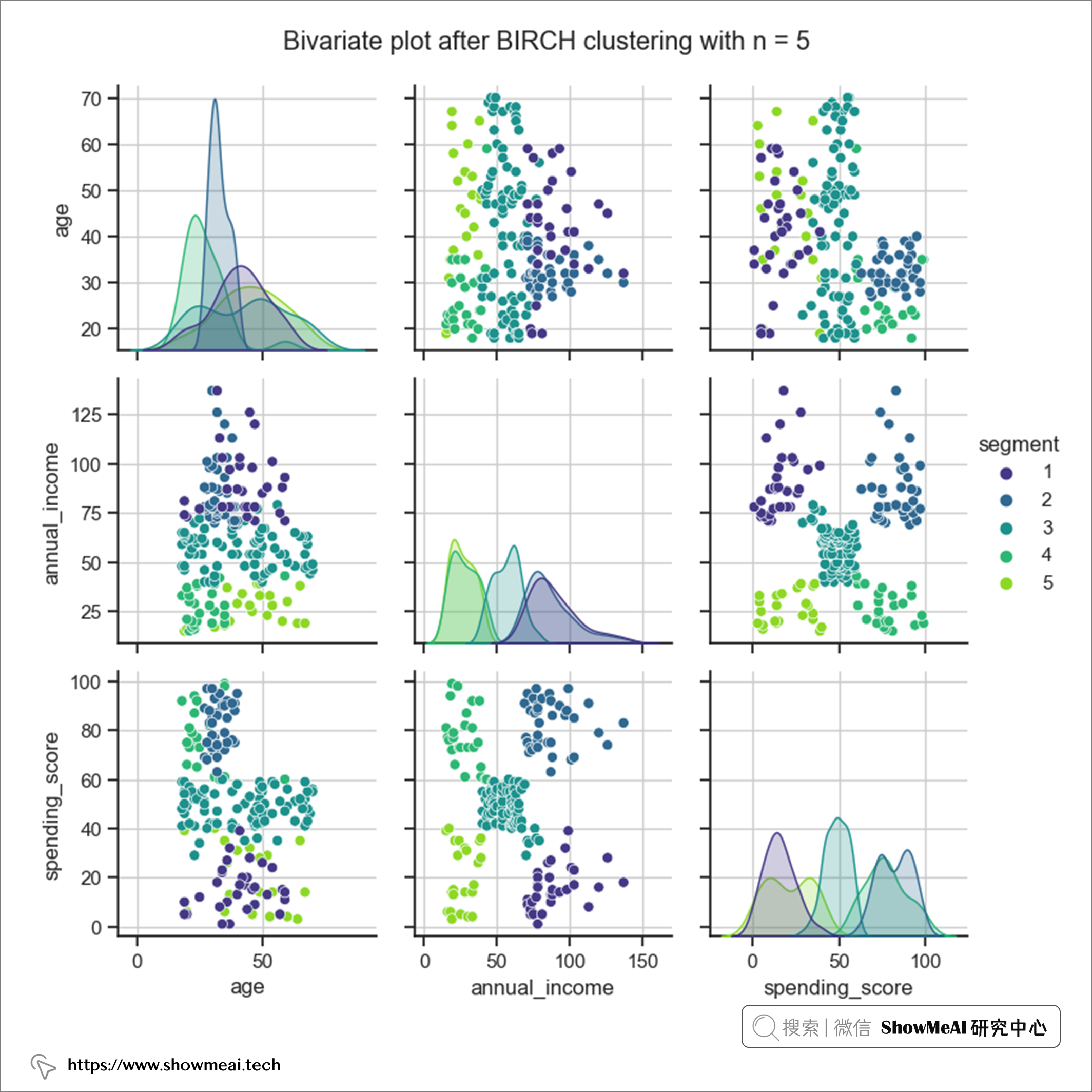
两种算法都得出相似的结果（不完全相同）。

④ 建模结果解释

我们来对聚类后的结果做一些解释分析，如下：

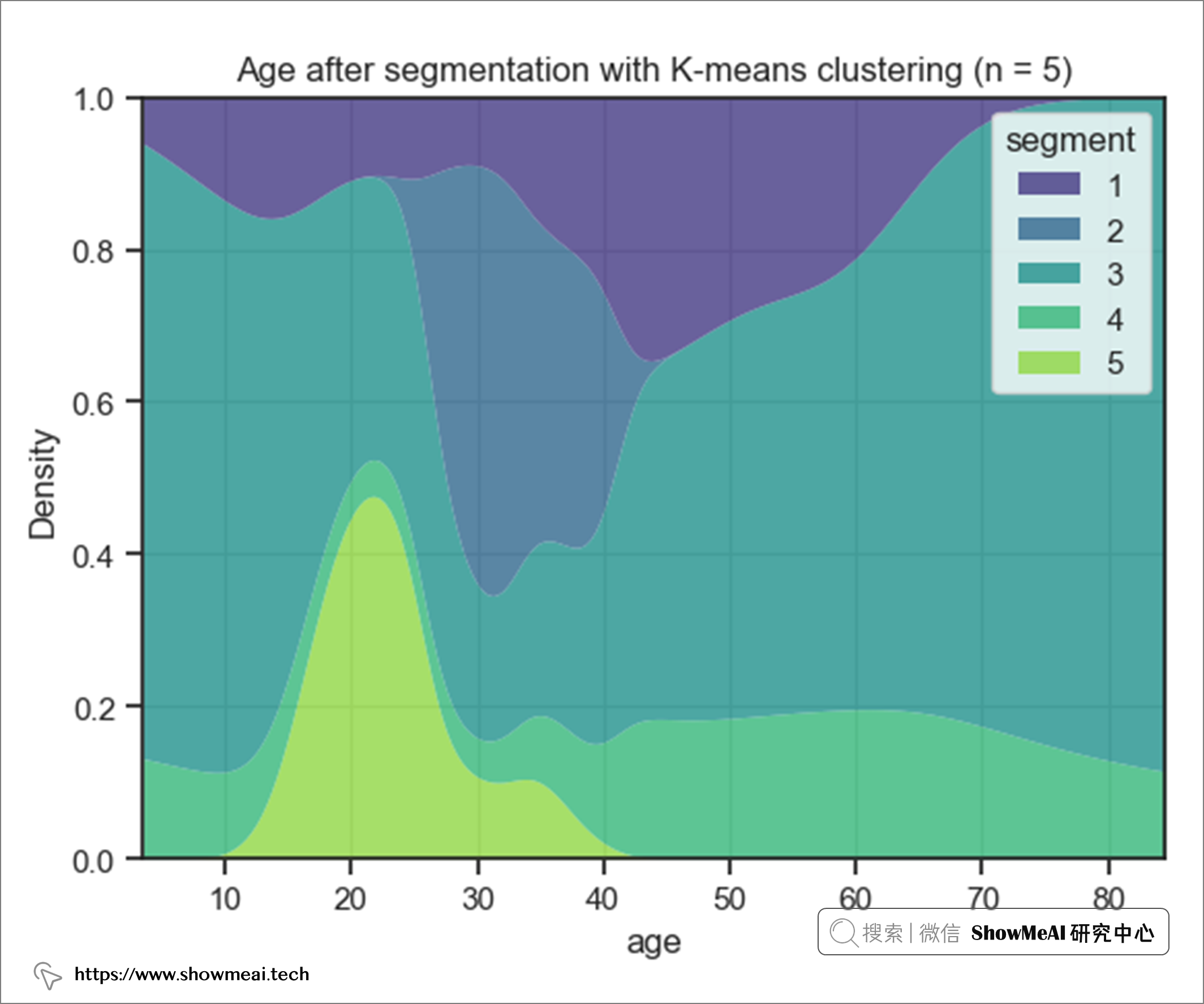
如上图所示，从年龄的角度来看，不同的用户簇有各自的一些分布特点：

  • 第 2 个用户簇 => 年龄在 27 到 40 岁之间 ，平均值为 33 岁。
  • 第 5 个用户簇 => 年龄在 18 到 35 岁之间 ，平均为 25 岁。

从收入维度来看：

  • 用户群4和5的年收入大致相等，大约为 26,000 美元。 → 低收入群体
  • 用户群1和2的年收入大致相等，这意味着大约 87,000 美元。 → 高收入群体
  • 用户群3是独立组，平均年收入为 55,000 美元。 → 中等收入群体

综合年龄和年收入得出以下结果。

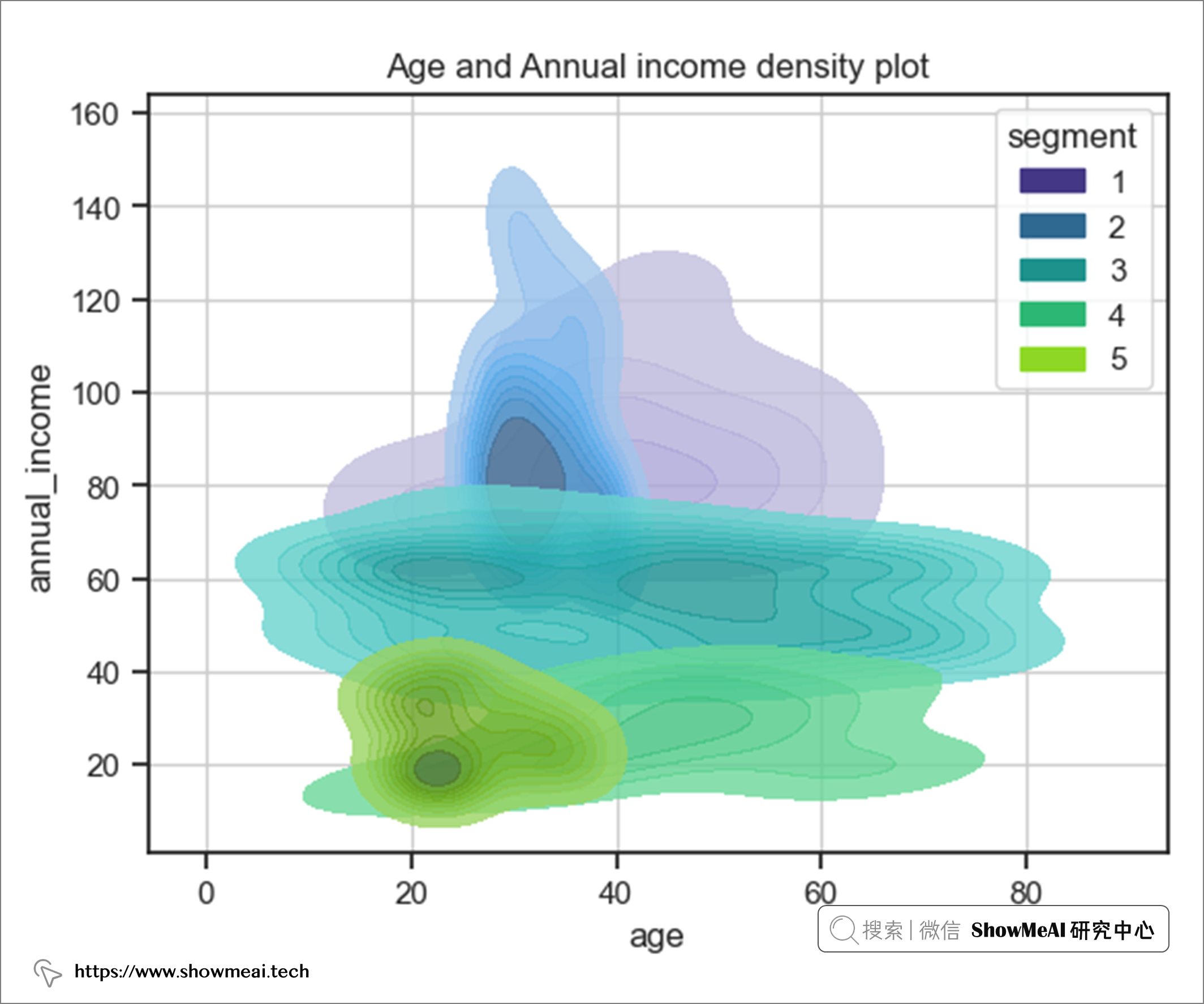
结果表明

  • 用户群2和5的年龄范围相同，但年收入有显着差异
  • 用户群4和5的年收入范围相同，但第 5 段属于青少年组（20-40 岁）

从花费的角度来看分组的用户群：

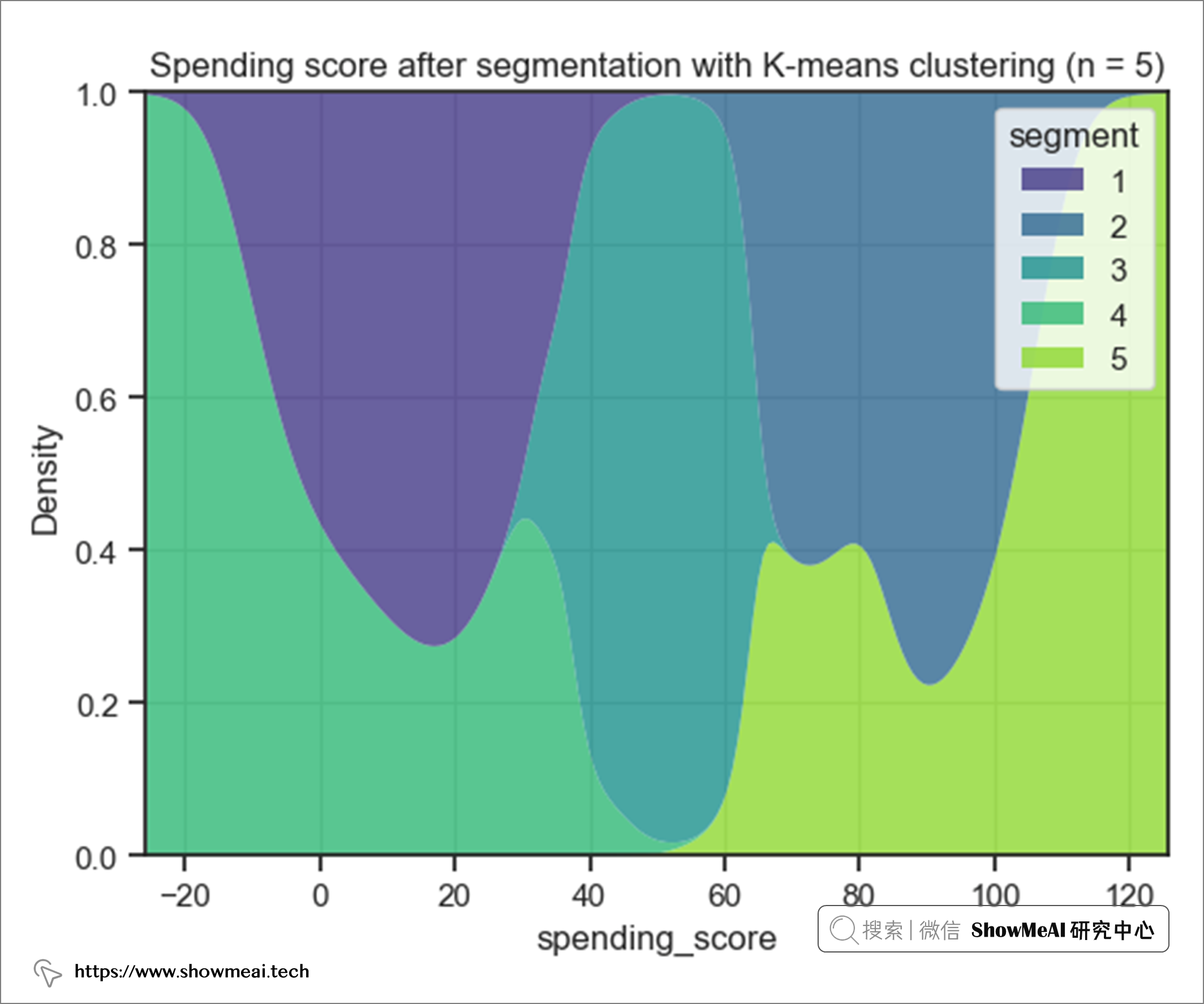
结果表明

  • 用户群5的 支出得分最高。
  • 用户群4的 支出得分最低。

综合支出分和年收入来看。

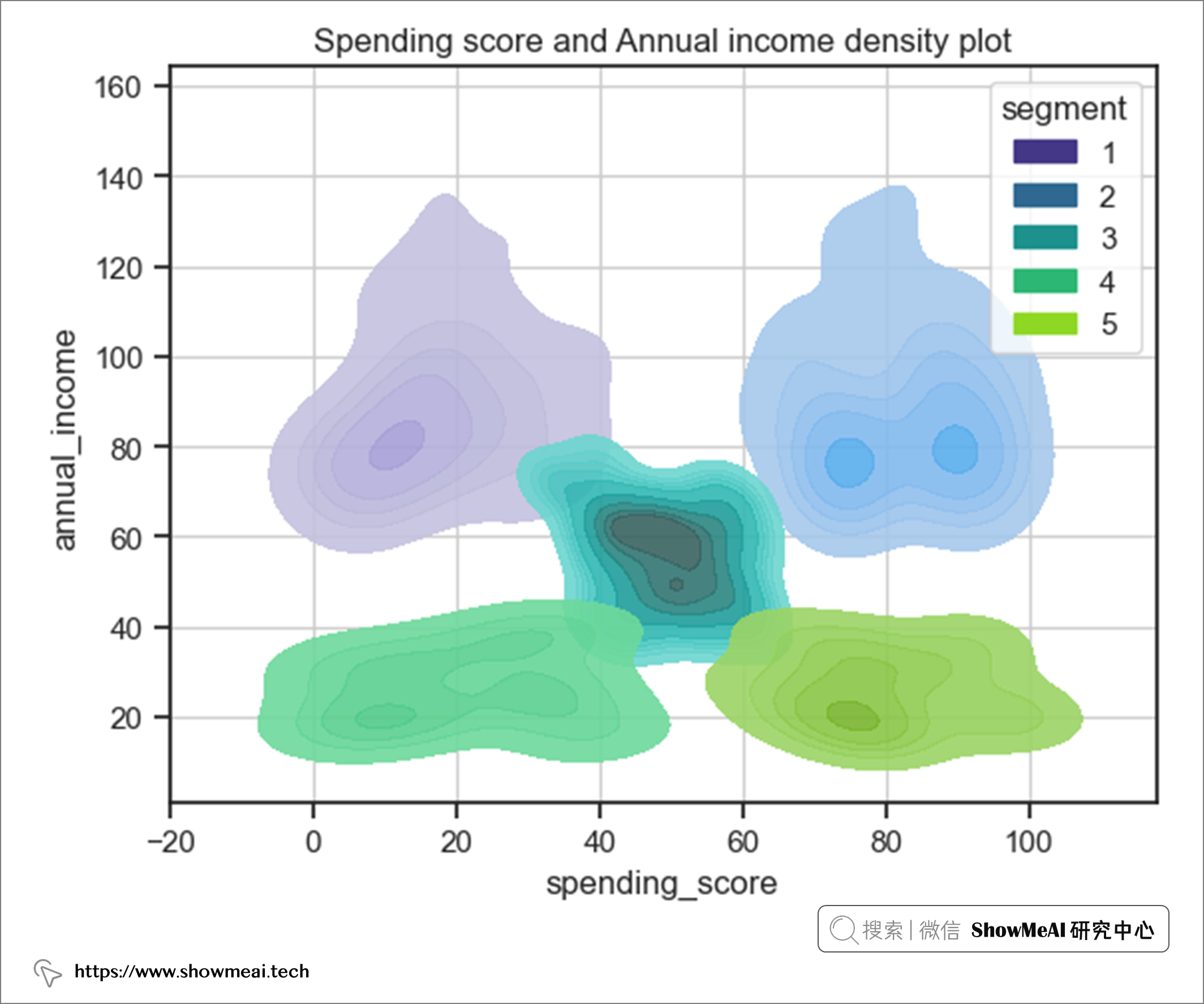
结果表明：

  • 用户群1和2的年收入范围相同，但支出分范围完全不同。
  • 用户群4和5的年收入范围相同，但支出分范围完全不同。

💡 结论

我们对各个用户群进行平均汇总，并绘制图表如下：

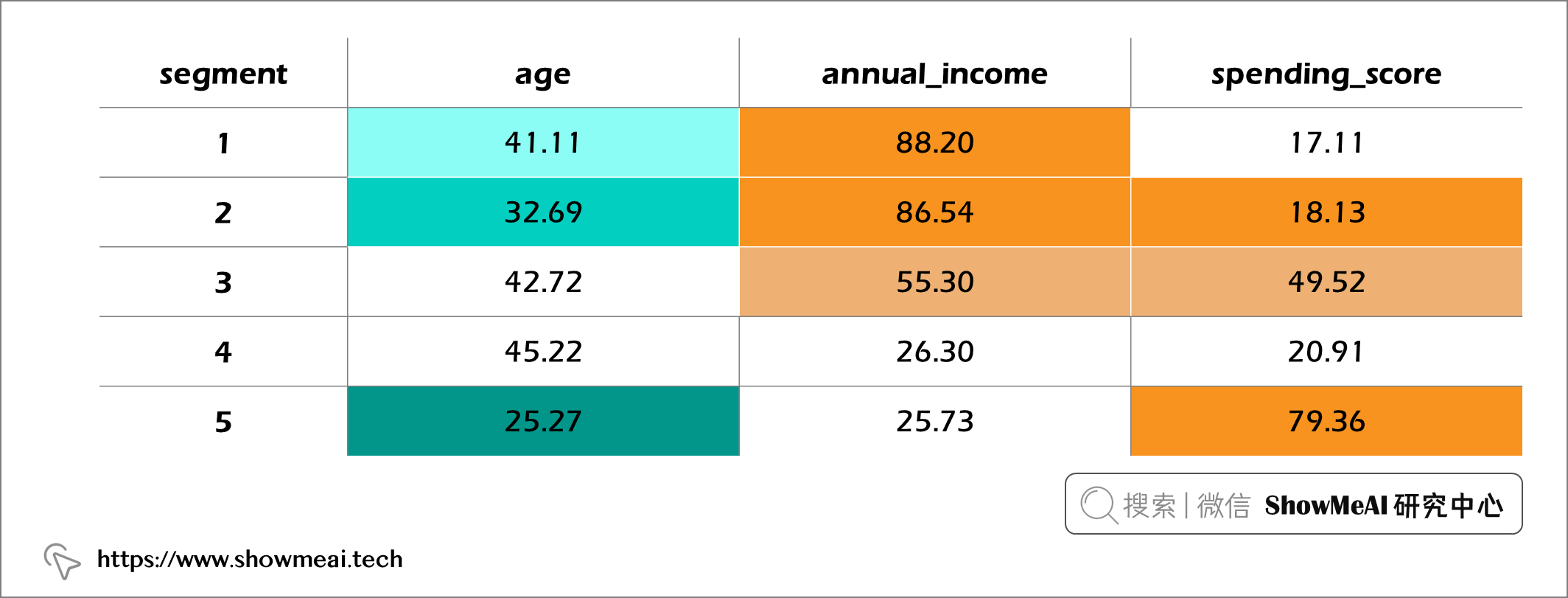
  • 用户群1是最高年收入组，但有最差的支出消费。 → 目前商城的产品并不是这部分客户的消费首选（非目标客户）。
  • 用户群2的平均年龄比第 1 段低 10 倍，但在相同年收入范围内的平均支出分数是 4 倍。
  • 用户群5是最高支出分数但是最低年收入组。 → 客户购买欲望强，但消费能力有限。

参考资料

posted @ 2022-11-20 14:37  ShowMeAI  阅读(620)  评论(0)  编辑  收藏  举报