深度学习与CV教程(4) | 神经网络与反向传播

ShowMeAI研究中心

作者：韩信子@ShowMeAI
教程地址：https://www.showmeai.tech/tutorials/37
本文地址：https://www.showmeai.tech/article-detail/263
声明：版权所有，转载请联系平台与作者并注明出处
收藏ShowMeAI查看更多精彩内容

Backpropagation and Neural Networks

本系列为 斯坦福CS231n 《深度学习与计算机视觉(Deep Learning for Computer Vision)》的全套学习笔记，对应的课程视频可以在这里查看。更多资料获取方式见文末。

引言

在上一篇 深度学习与CV教程(3) | 损失函数与最优化 内容中，我们给大家介绍了线性模型的损失函数构建与梯度下降等优化算法，【本篇内容】ShowMeAI给大家切入到神经网络，讲解神经网络计算图与反向传播以及神经网络结构等相关知识。

本篇重点

神经网络计算图
反向传播
神经网络结构

1.反向传播算法

神经网络的训练，应用到的梯度下降等方法，需要计算损失函数的梯度，而其中最核心的知识之一是反向传播，它是利用数学中链式法则递归求解复杂函数梯度的方法。而像tensorflow、pytorch等主流AI工具库最核心的智能之处也是能够自动微分，在本节内容中ShowMeAI就结合cs231n的第4讲内容展开讲解一下神经网络的计算图和反向传播。

关于神经网络反向传播的解释也可以参考ShowMeAI的 深度学习教程 | 吴恩达专项课程 · 全套笔记解读 中的文章 神经网络基础、浅层神经网络、深层神经网络 里对于不同深度的网络前向计算和反向传播的讲解

1.1 标量形式反向传播

1) 引例

我们来看一个简单的例子，函数为 $f(x,y,z) = (x + y) z$。初值 $x = -2$，$y = 5$，$z = -4$。这是一个可以直接微分的表达式，但是我们使用一种有助于直观理解反向传播的方法来辅助理解。

下图是整个计算的线路图，绿字部分是函数值，红字是梯度。（梯度是一个向量，但通常将对 $x$ 的偏导数称为 $x$ 上的梯度。）

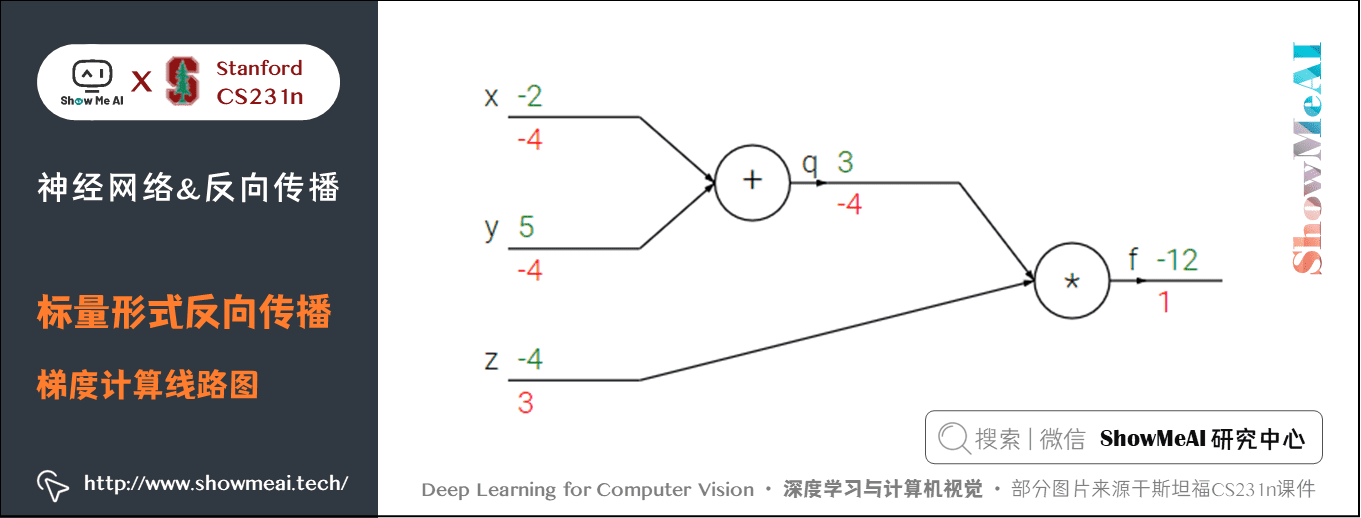
标量形式反向传播; 梯度计算线路图

上述公式可以分为2部分， $q = x + y$ 和 $f = q z$。它们都很简单可以直接写出梯度表达式：

$f$ 是 $q$ 和 $z$ 的乘积，所以 $\frac{\partial f}{\partial q} = z=-4$，$\frac{\partial f}{\partial z} = q=3$
$q$ 是 $x$ 和 $y$ 相加，所以 $\frac{\partial q}{\partial x} = 1$，$\frac{\partial q}{\partial y} = 1$

我们对 $q$ 上的梯度不关心（ $\frac{\partial f}{\partial q}$ 没有用处）。我们关心 $f$ 对于 $x,y,z$ 的梯度。链式法则告诉我们可以用「乘法」将这些梯度表达式链接起来，比如

\[\frac{\partial f}{\partial x} = \frac{\partial f}{\partial q} \frac{\partial q}{\partial x} =-4 \]

同理， $\frac{\partial f}{\partial y} =-4$，还有一点是 $\frac{\partial f}{\partial f}=1$

前向传播从输入计算到输出（绿色），反向传播从尾部开始，根据链式法则递归地向前计算梯度（显示为红色），一直到网络的输入端。可以认为，梯度是从计算链路中回流。

上述计算的参考 python 实现代码如下：

# 设置输入值
x = -2; y = 5; z = -4

# 进行前向传播
q = x + y # q 是 3
f = q * z # f 是 -12

# 进行反向传播:
# 首先回传到 f = q * z
dfdz = q # df/dz = q, 所以关于z的梯度是3
dfdq = z # df/dq = z, 所以关于q的梯度是-4
# 现在回传到q = x + y
dfdx = 1.0 * dfdq # dq/dx = 1. 这里的乘法是因为链式法则。所以df/dx是-4
dfdy = 1.0 * dfdq # dq/dy = 1.所以df/dy是-4

'''一般可以省略df'''

2) 直观理解反向传播

反向传播是一个优美的局部过程。

以下图为例，在整个计算线路图中，会给每个门单元（也就是 $f$ 结点）一些输入值 $x$ , $y$ 并立即计算这个门单元的输出值 $z$ ，和当前节点输出值关于输入值的局部梯度（local gradient） $\frac{\partial z}{\partial x}$ 和 $\frac{\partial z}{\partial y}$ 。

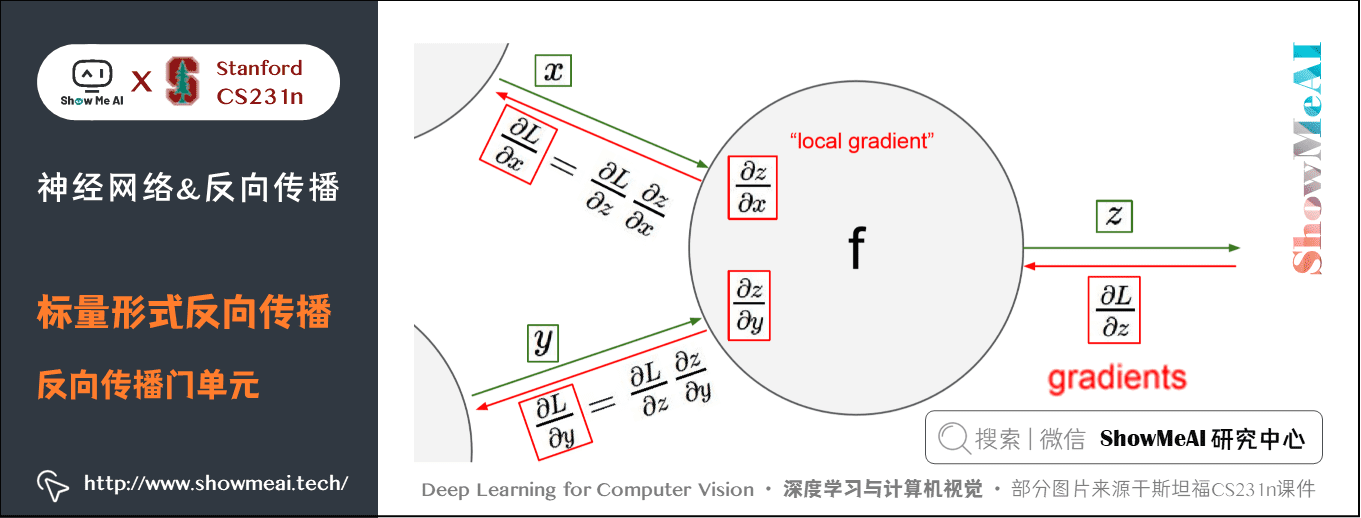
标量形式反向传播; 反向传播门单元

门单元的这两个计算在前向传播中是完全独立的，它无需知道计算线路中的其他单元的计算细节。但在反向传播的过程中，门单元将获得整个网络的最终输出值在自己的输出值上的梯度 $\frac{\partial L}{\partial z}$ 。

根据链式法则，整个网络的输出对该门单元的每个输入值的梯度，要用回传梯度乘以它的输出对输入的局部梯度，得到 $\frac{\partial L}{\partial x}$ 和 $\frac{\partial L}{\partial y}$ 。这两个值又可以作为前面门单元的回传梯度。

因此，反向传播可以看做是门单元之间在通过梯度信号相互通信，只要让它们的输入沿着梯度方向变化，无论它们自己的输出值在何种程度上升或降低，都是为了让整个网络的输出值更高。

比如引例中 $x,y$ 梯度都是 $-4$，所以让 $x,y$ 减小后，$q$ 的值虽然也会减小，但最终的输出值 $f$ 会增大（当然损失函数要的是最小）。

3) 加法门、乘法门和max门

引例中用到了两种门单元：加法和乘法。

加法求偏导： $f(x,y) = x + y \rightarrow \frac{\partial f}{\partial x} = 1 \frac{\partial f}{\partial y} = 1$
乘法求偏导： $f(x,y) = x y \rightarrow \frac{\partial f}{\partial x} = y \frac{\partial f}{\partial y} = x$

除此之外，常用的操作还包括取最大值：

\[\begin{aligned} f(x,y) &= \max(x, y) \\ \rightarrow \frac{\partial f}{\partial x} &= \mathbb{1}(x \ge y)\\ \frac{\partial f}{\partial y} &\mathbb{1}(y \ge x) \end{aligned} \]

上式含义为：若该变量比另一个变量大，那么梯度是 $1$，反之为 $0$。

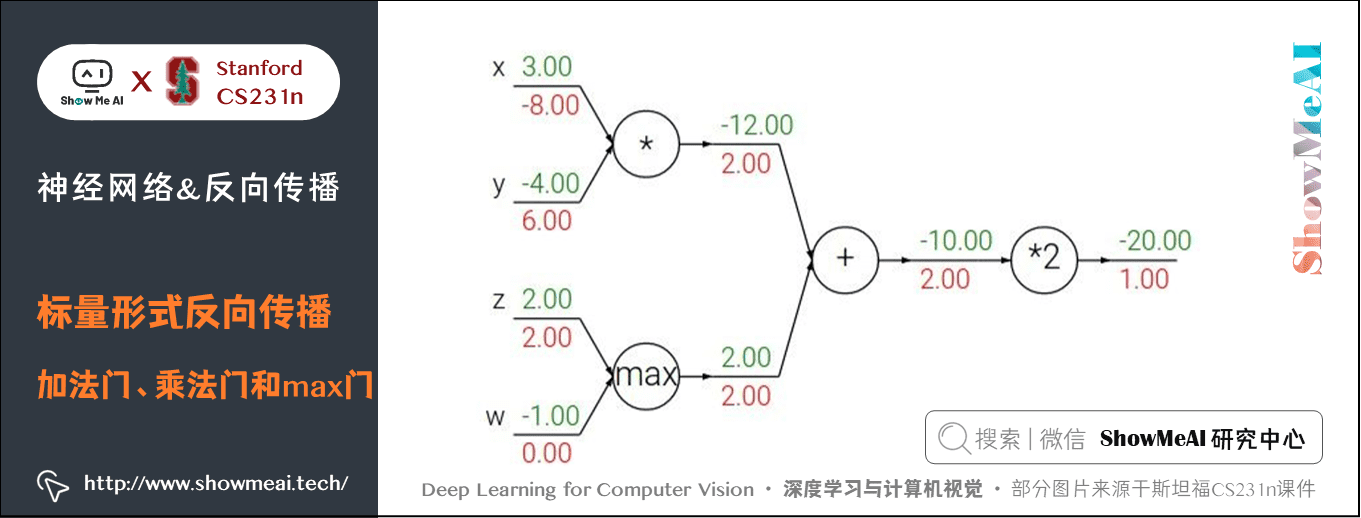
标量形式反向传播; 加法门、乘法门和max门

加法门单元是梯度分配器，输入的梯度都等于输出的梯度，这一行为与输入值在前向传播时的值无关；
乘法门单元是梯度转换器，输入的梯度等于输出梯度乘以另一个输入的值，或者乘以倍数 $a$（$ax$ 的形式乘法门单元）；max 门单元是梯度路由器，输入值大的梯度等于输出梯度，小的为 $0$。

乘法门单元的局部梯度就是输入值，但是是相互交换之后的，然后根据链式法则乘以输出值的梯度。基于此，如果乘法门单元的其中一个输入非常小，而另一个输入非常大，那么乘法门会把大的梯度分配给小的输入，把小的梯度分配给大的输入。

以我们之前讲到的线性分类器为例，权重和输入进行点积 $w^Tx_i$ ，这说明输入数据的大小对于权重梯度的大小有影响。具体的，如在计算过程中对所有输入数据样本 $x_i$ 乘以 100，那么权重的梯度将会增大 100 倍，这样就必须降低学习率来弥补。

也说明了数据预处理有很重要的作用，它即使只是有微小变化，也会产生巨大影响。

对于梯度在计算线路中是如何流动的有一个直观的理解，可以帮助调试神经网络。

4) 复杂示例

我们来看一个复杂一点的例子：

\[f(w,x) = \frac{1}{1+e^{-(w_0x_0 + w_1x_1 + w_2)}} \]

这个表达式需要使用新的门单元：

\[\begin{aligned} f(x) &= \frac{1}{x} \\ \rightarrow \frac{df}{dx} &=- \frac{1}{x^2}\ f_c(x) = c + x \\ \rightarrow \frac{df}{dx} &= 1 \ f(x) = e^x \\ \rightarrow \frac{df}{dx} &= e^x \ f_a(x) = ax \\ \rightarrow \frac{df}{dx} &= a \end{aligned} \]

计算过程如下：

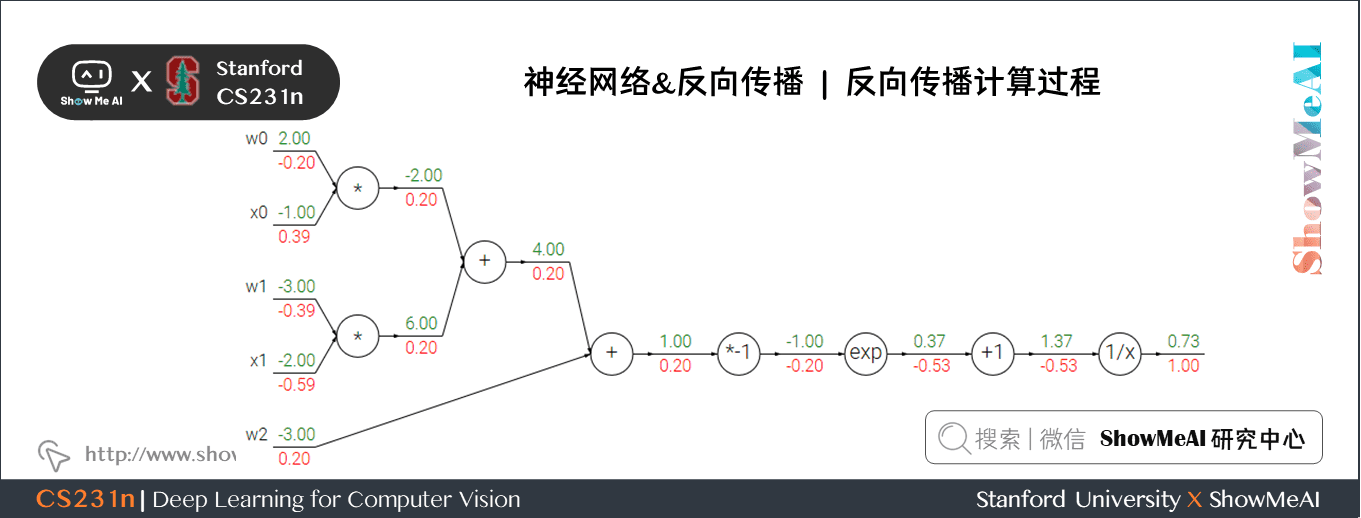
神经网络&反向传播; 反向传播计算过程

对于 $1/x$ 门单元，回传梯度是 $1$，局部梯度是 $-1/x^2=-1/1.37^2=-0.53$ ，所以输入梯度为 $1 \times -0.53 = -0.53$；$+1$ 门单元不改变梯度还是 $-0.53$
exp门单元局部梯度是 $e^x=e^{-1}$ ，然后乘回传梯度 $-0.53$ 结果约为 $-0.2$
乘 $-1$ 门单元会将梯度加负号变为 $0.2$
加法门单元会分配梯度，所以从上到下三个加法分支都是 $0.2$
最后两个乘法单元会转换梯度，把回传梯度乘另一个输入值作为自己的梯度，得到 $-0.2$、$0.4$、$-0.4$、$-0.6$

5) Sigmoid门单元

我们可以将任何可微分的函数视作「门」。可以将多个门组合成一个门，也可以根据需要将一个函数拆成多个门。我们观察可以发现，最右侧四个门单元可以合成一个门单元，$\sigma(x) = \frac{1}{1+e^{-x}}$ ，这个函数称为 sigmoid 函数。

sigmoid 函数可以微分：

\[\frac{d\sigma(x)}{dx} = \frac{e^{-x}}{(1+e^{-x})^2} = \left( \frac{1 + e^{-x} - 1}{1 + e^{-x}} \right) \left( \frac{1}{1+e^{-x}} \right) = \left( 1 - \sigma(x) \right) \sigma(x) \]

所以上面的例子中已经计算出 $\sigma(x)=0.73$ ，可以直接计算出乘 $-1$ 门单元输入值的梯度为：$1 \ast (1-0.73) \ast0.73~=0.2$，计算简化很多。

上面这个例子的反向传播的参考 python 实现代码如下：

# 假设一些随机数据和权重
w = [2,-3,-3] 
x = [-1, -2]

# 前向传播，计算输出值
dot = w[0]*x[0] + w[1]*x[1] + w[2]
f = 1.0 / (1 + math.exp(-dot)) # sigmoid函数

# 反向传播，计算梯度
ddot = (1 - f) * f # 点积变量的梯度, 使用sigmoid函数求导
dx = [w[0] * ddot, w[1] * ddot] # 回传到x
dw = [x[0] * ddot, x[1] * ddot, 1.0 * ddot] # 回传到w
# 最终得到输入的梯度

在实际操作中，有时候我们会把前向传播分成不同的阶段，这样可以让反向传播过程更加简洁。比如创建一个中间变量 $dot$，存放 $w$ 和 $x$ 的点乘结果。在反向传播时，可以很快计算出装着 $w$ 和 $x$ 等的梯度的对应的变量（比如 $ddot$，$dx$ 和 $dw$）。

本篇内容列了很多例子，我们希望通过这些例子讲解「前向传播」与「反向传播」过程，哪些函数可以被组合成门，如何简化，这样他们可以“链”在一起，让代码量更少，效率更高。

6) 分段计算示例

\[f(x,y) = \frac{x + \sigma(y)}{\sigma(x) + (x+y)^2} \]

这个表达式只是为了实践反向传播，如果直接对 $x,y$ 求导，运算量将会很大。下面先代码实现前向传播：

x = 3  # 例子数值
y = -4

# 前向传播
sigy = 1.0 / (1 + math.exp(-y)) # 分子中的sigmoid         #(1)
num = x + sigy # 分子                                    #(2)
sigx = 1.0 / (1 + math.exp(-x)) # 分母中的sigmoid         #(3)
xpy = x + y                                              #(4)
xpysqr = xpy**2                                          #(5)
den = sigx + xpysqr # 分母                                #(6)
invden = 1.0 / den                                       #(7)
f = num * invden

代码创建了多个中间变量，每个都是比较简单的表达式，它们计算局部梯度的方法是已知的。可以给我们计算反向传播带来很多便利：

我们对前向传播时产生的每个变量 $ (sigy, num, sigx, xpy, xpysqr, den, invden)$ 进行回传。
我们用同样数量的变量（以 d 开头），存储对应变量的梯度。
注意：反向传播的每一小块中都将包含了表达式的局部梯度，然后根据使用链式法则乘以上游梯度。对于每行代码，我们将指明其对应的是前向传播的哪部分，序号对应。

# 回传 f = num * invden
dnum = invden # 分子的梯度                                         #(8)
dinvden = num # 分母的梯度                                         #(8)
# 回传 invden = 1.0 / den 
dden = (-1.0 / (den**2)) * dinvden                                #(7)
# 回传 den = sigx + xpysqr
dsigx = (1) * dden                                                #(6)
dxpysqr = (1) * dden                                              #(6)
# 回传 xpysqr = xpy**2
dxpy = (2 * xpy) * dxpysqr                                        #(5)
# 回传 xpy = x + y
dx = (1) * dxpy                                                   #(4)
dy = (1) * dxpy                                                   #(4)
# 回传 sigx = 1.0 / (1 + math.exp(-x))
dx += ((1 - sigx) * sigx) * dsigx # 注意这里用的是+=，下面有解释    #(3)
# 回传 num = x + sigy
dx += (1) * dnum                                                  #(2)
dsigy = (1) * dnum                                                #(2)
# 回传 sigy = 1.0 / (1 + math.exp(-y))
dy += ((1 - sigy) * sigy) * dsigy

补充解释：

①对前向传播变量进行缓存

在计算反向传播时，前向传播过程中得到的一些中间变量非常有用。
实现过程中，在代码里对这些中间变量进行缓存，这样在反向传播的时候也能用上它们。

②在不同分支的梯度要相加

如果变量 $x,y$ 在前向传播的表达式中出现多次，那么进行反向传播的时候就要非常小心，要使用$+=$ 而不是 $=$ 来累计这些变量的梯度。
根据微积分中的多元链式法则，如果变量在线路中走向不同的分支，那么梯度在回传的时候，应该累加。即：

\[\frac{\partial f}{\partial x} =\sum_{q_i}\frac{\partial f}{\partial q_i}\frac{\partial q_i}{\partial x} \]

7) 实际应用

如果有一个计算图，已经拆分成门单元的形式，那么主类代码结构如下：

class ComputationalGraph(object):
    # ...
    def forward(self, inputs):
        # 把inputs传递给输入门单元
        # 前向传播计算图
        # 遍历所有从后向前按顺序排列的门单元
        for gate in self.graph.nodes_topologically_sorted(): 
            gate.forward()  # 每个门单元都有一个前向传播函数
        return loss  # 最终输出损失

    def backward(self):
        # 反向遍历门单元
        for gate in reversed(self.graph.nodes_topologically_sorted()): 
            gate.backward()  # 反向传播函数应用链式法则
        return inputs_gradients  # 输出梯度
        return inputs_gradients  # 输出梯度

门单元类可以这么定义，比如一个乘法单元：

class MultiplyGate(object):
    def forward(self, x, y):
        z = x*y
        self.x = x
        self.y = y
        return z

    def backward(self, dz):
        dx = self.y * dz
        dy = self.x * dz
        return [dx, dy]

1.2 向量形式反向传播

先考虑一个简单的例子，比如：

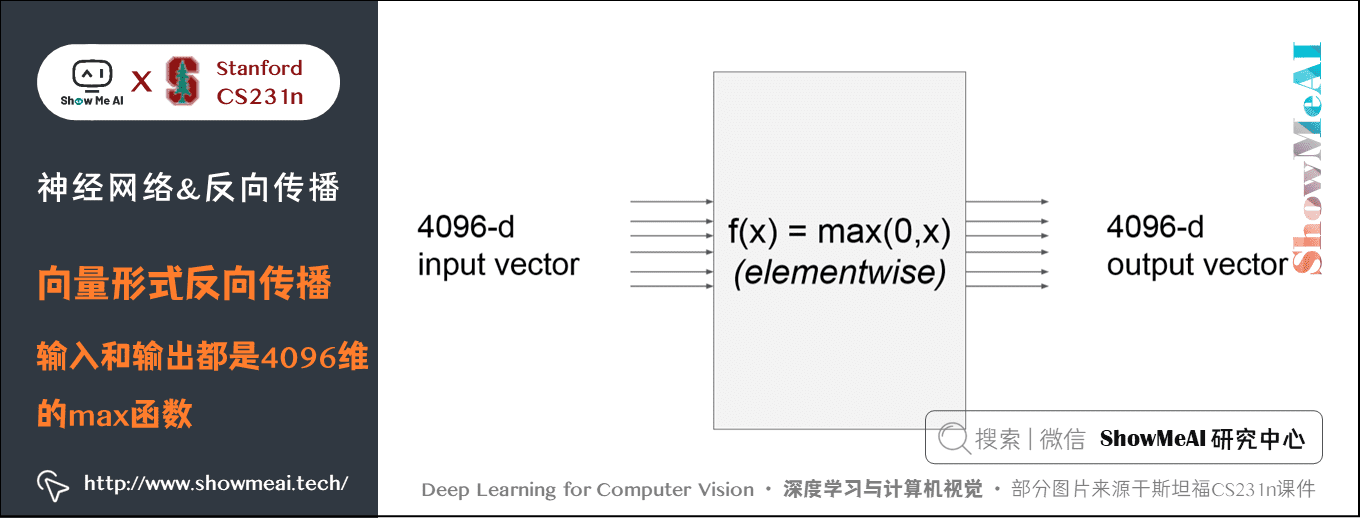
向量形式反向传播; 输入和输出都是4096维的max函数

这个 $max$ 函数对输入向量 $x$ 的每个元素都和 $0$ 比较输出最大值，因此输出向量的维度也是 $4096$维。此时的梯度是雅可比矩阵，即输出的每个元素对输入的每个元素求偏导组成的矩阵。

假如输入 $x$ 是 $n$ 维的向量，输出 $y$ 是 $m$ 维的向量，则 $y_1,y_2, \cdots,y_m$ 都是 $(x_1-x_n)$ 的函数，得到的雅克比矩阵如下所示：

\[\left[\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{1}}{\partial x_{n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_{m}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right] \]

那么这个例子的雅克比矩阵是 $[4096 \times 4096]$ 维的，输出有 $4096$ 个元素，每一个都要求 $4096$ 次偏导。其实仔细观察发现，这个例子输出的每个元素都只和输入相应位置的元素有关，因此得到的是一个对角矩阵。

实际应用的时候，往往 100 个 $x$ 同时输入，此时雅克比矩阵是一个 $[409600 \times 409600]$ 的对角矩阵，当然只是针对这里的 $f$ 函数。

实际上，完全写出并存储雅可比矩阵不太可能，因为维度极其大。

1) 一个例子

目标公式为： $f(x,W)=\vert \vert W\cdot x \vert \vert ^2=\sum_{i=1}^n (W\cdot x)_{i}^2$

其中 $x$ 是 $n$ 维的向量，$W$ 是 $n \times n$ 的矩阵。

设 $q=W\cdot x$ ,于是得到下面的式子：

\[\begin{array}{l} q=W \cdot x=\left(\begin{array}{c} W_{1,1} x_{1}+\cdots+W_{1, n} x_{n} \\ \vdots \\ W_{n, 1} x_{1}+\cdots+W_{n, n} x_{n} \end{array}\right) \\ \end{array} \]

\[f(q)=\|q\|^{2}=q_{1}^{2}+\cdots+q_{n}^{2} \]

可以看出：

$\frac{\partial f}{\partial q_i}=2q_i$ 从而得到 $f$ 对 $q$ 的梯度为 $2q$ ；
$\frac{\partial q_k}{\partial W_{i, j}}=1{i=k}x_j$，$\frac{\partial f}{\partial W_{i, j}}=\sum_{k=1}^n\frac{\partial f}{\partial q_k}\frac{\partial q_k}{\partial W_{i, j}}=\sum_{k=1}^n(2q_k)1{i=k}x_j=2q_ix_j$，从而得到 $f$ 对 $W$ 的梯度为 $2q\cdot x^T$ ；
$\frac{\partial q_k}{\partial x_i}=W_{k,i}$ ， $\frac{\partial f}{\partial x_i}=\sum_{k=1}^n\frac{\partial f}{\partial q_k}\frac{\partial q_k}{\partial x_i}=\sum_{k=1}^n(2q_k)W_{k,i}$ ，从而得到 $f$ 对 $x$ 的梯度为 $2W^T\cdot q$

下面为计算图：

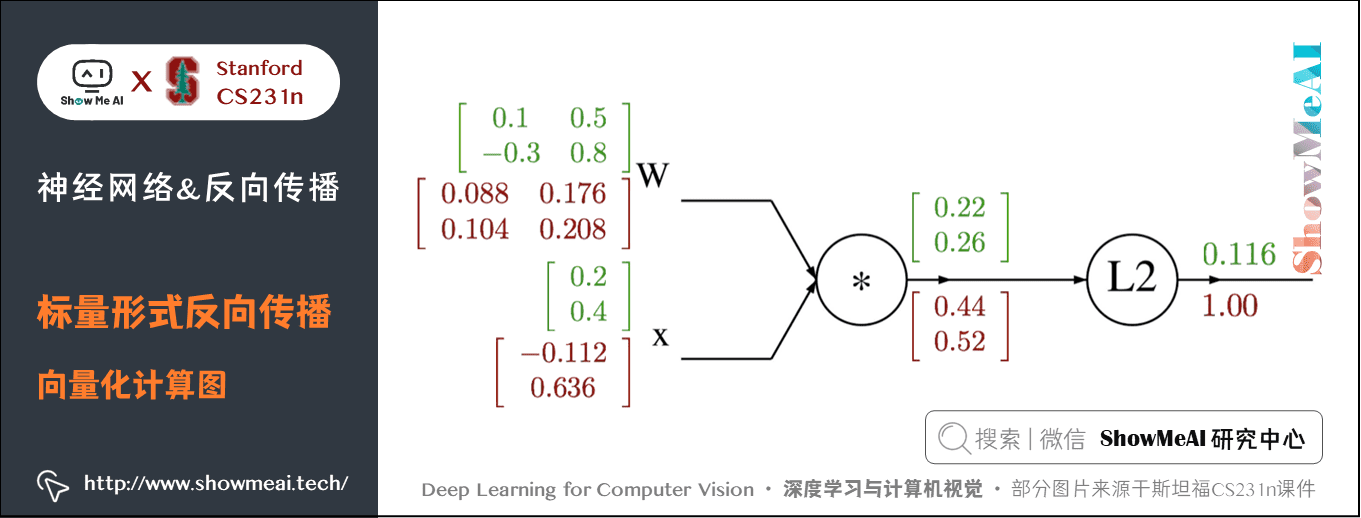
标量形式反向传播; 向量化计算图

2) 代码实现

import numpy as np

# 初值
W = np.array([[0.1, 0.5], [-0.3, 0.8]])
x = np.array([0.2, 0.4]).reshape((2, 1))  # 为了保证dq.dot(x.T)是一个矩阵而不是实数

# 前向传播
q = W.dot(x)
f = np.sum(np.square(q), axis=0)

# 反向传播
# 回传 f = np.sum(np.square(q), axis=0)
dq = 2*q
# 回传 q = W.dot(x)
dW = dq.dot(x.T)  # x.T就是对矩阵x进行转置
dx = W.T.dot(dq)

注意：要分析维度！不要去记忆 $dW$ 和 $dx$ 的表达式，因为它们很容易通过维度推导出来。

权重的梯度 $dW$ 的尺寸肯定和权重矩阵 $W$ 的尺寸是一样的

这里的 $f$ 输出是一个实数，所以 $dW$和 $W$ 的形状一致。
如果考虑 $dq/dW$ 的话，如果按照雅克比矩阵的定义，$dq/dw$ 应该是 $2 \times 2 \times 2$ 维，为了减小计算量，就令其等于 $x$。
其实完全不用考虑那么复杂，因为最终的损失函数一定是一个实数，所以每个门单元的输入梯度一定和原输入形状相同。 关于这点的说明，可以点击这里，官网进行了详细的推导。
而这又是由 $x$ 和 $dq$ 的矩阵乘法决定的，总有一个方式是能够让维度之间能够对的上的。

例如，$x$ 的尺寸是 $[2 \times 1]$，$dq$ 的尺寸是 $[2 \times 1]$，如果你想要 $dW$ 和 $W$ 的尺寸是 $[2 \times 2]$，那就要 dq.dot(x.T)，如果是 x.T.dot(dq) 结果就不对了。（$dq$ 是回传梯度不能转置！）

2.神经网络简介

2.1 神经网络算法介绍

在不诉诸大脑的类比的情况下，依然是可以对神经网络算法进行介绍的。

在线性分类一节中，在给出图像的情况下，是使用 $Wx$ 来计算不同视觉类别的评分，其中 $W$ 是一个矩阵，$x$ 是一个输入列向量，它包含了图像的全部像素数据。在使用数据库 CIFAR-10 的案例中，$x$ 是一个 $[3072 \times 1]$ 的列向量，$W$ 是一个 $[10 \times 3072]$ 的矩阵，所以输出的评分是一个包含10个分类评分的向量。

一个两层的神经网络算法则不同，它的计算公式是 $s = W_2 \max(0, W_1 x)$ 。

$W_1$ 的含义：举例来说，它可以是一个 $[100 \times 3072]$ 的矩阵，其作用是将图像转化为一个100维的过渡向量，比如马的图片有头朝左和朝右，会分别得到一个分数。

函数 $max(0,-)$ 是非线性的，它会作用到每个元素。这个非线性函数有多种选择，大家在后续激活函数里会再看到。现在看到的这个函数是最常用的ReLU激活函数，它将所有小于 $0$ 的值变成 $0$。

矩阵 $W_2$ 的尺寸是 $[10 \times 100]$，会对中间层的得分进行加权求和，因此将得到 10 个数字，这10个数字可以解释为是分类的评分。

注意：非线性函数在计算上是至关重要的，如果略去这一步，那么两个矩阵将会合二为一，对于分类的评分计算将重新变成关于输入的线性函数。这个非线性函数就是改变的关键点。

参数 $W_1$ **,$ **W_2$ 将通过随机梯度下降来学习到，他们的梯度在反向传播过程中，通过链式法则来求导计算得出。

一个三层的神经网络可以类比地看做 $s = W_3 \max(0, W_2 \max(0, W_1 x))$ ，其中$W_1$, $W_2$ ,$W_3$ 是需要进行学习的参数。中间隐层的尺寸是网络的超参数，后续将学习如何设置它们。现在让我们先从神经元或者网络的角度理解上述计算。

两层神经网络参考代码实现如下，中间层使用 sigmoid 函数：

import numpy as np
from numpy.random import randn

N, D_in, H, D_out = 64, 1000, 100, 10
# x 是64x1000的矩阵，y是64x10的矩阵
x, y = randn(N, D_in), randn(N, D_out)
# w1是1000x100的矩阵，w2是100x10的矩阵
w1, w2 = randn(D_in, H), randn(H, D_out)

# 迭代10000次，损失达到0.0001级
for t in range(10000):
    h = 1 / (1 + np.exp(-x.dot(w1)))  # 激活函数使用sigmoid函数，中间层
    y_pred = h.dot(w2)
    loss = np.square(y_pred - y).sum()  # 损失使用 L2 范数
    print(str(t)+': '+str(loss))

    # 反向传播
    grad_y_pred = 2.0 * (y_pred - y)
    grad_w2 = h.T.dot(grad_y_pred)
    grad_h = grad_y_pred.dot(w2.T)
    # grad_xw1 = grad_h*h*(1-h)
    grad_w1 = x.T.dot(grad_h*h*(1-h))

    # 学习率是0.0001
    w1 -= 1e-4 * grad_w1
    w2 -= 1e-4 * grad_w2

2.2 神经网络与真实的神经对比

神经网络算法很多时候是受生物神经系统启发而简化模拟得到的。

大脑的基本计算单位是神经元（neuron） 。人类的神经系统中大约有 860 亿个神经元，它们被大约 1014 - 1015 个突触（synapses） 连接起来。下图的上方是一个生物学的神经元，下方是一个简化的常用数学模型。每个神经元都从它的树突（dendrites） 获得输入信号，然后沿着它唯一的轴突（axon） 产生输出信号。轴突在末端会逐渐分枝，通过突触和其他神经元的树突相连。

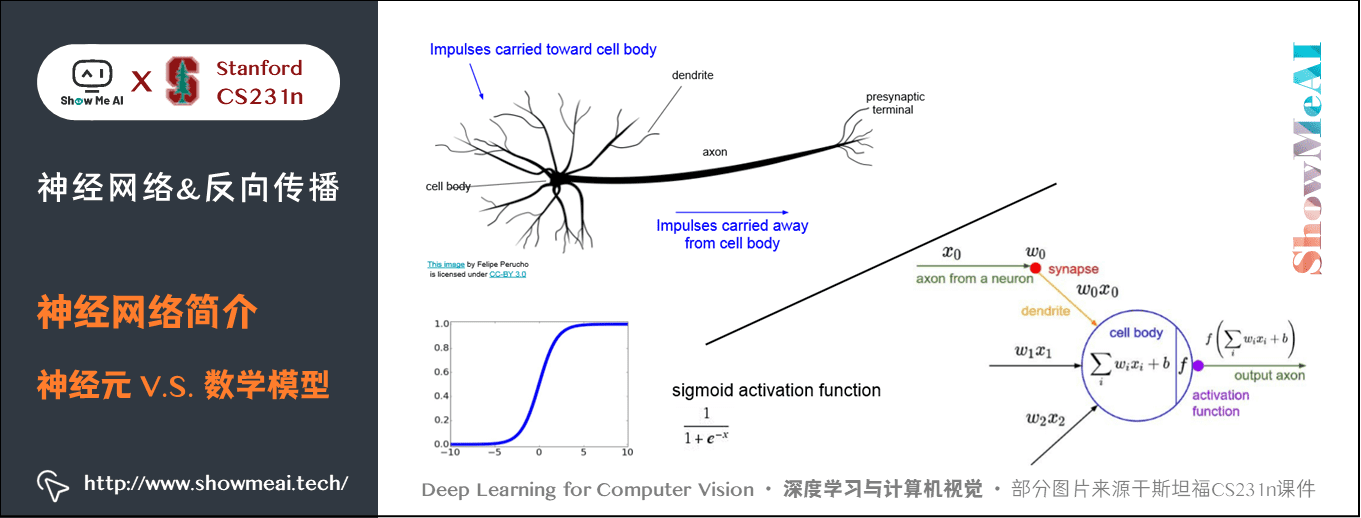
神经网络简介; 神经元 V.S. 数学模型

在神经元的计算模型中，沿着轴突传播的信号（比如 $x_0$ ）将基于突触的突触强度（比如 $w_0$ ），与其他神经元的树突进行乘法交互（比如 $w_0 x_0$ ）。

对应的想法是，突触的强度（也就是权重 $w$ ），是可学习的且可以控制一个神经元对于另一个神经元的影响强度（还可以控制影响方向：使其兴奋（正权重）或使其抑制（负权重））。

树突将信号传递到细胞体，信号在细胞体中相加。如果最终之和高于某个阈值，那么神经元将会「激活」，向其轴突输出一个峰值信号。

在计算模型中，我们假设峰值信号的准确时间点不重要，是激活信号的频率在交流信息。基于这个速率编码的观点，将神经元的激活率建模为激活函数（activation function） $f$ ，它表达了轴突上激活信号的频率。

由于历史原因，激活函数常常选择使用sigmoid函数 $\sigma$ ，该函数输入实数值（求和后的信号强度），然后将输入值压缩到 $0\sim 1$ 之间。在本节后面部分会看到这些激活函数的各种细节。

这里的激活函数 $f$ 采用的是 sigmoid 函数，代码如下：

class Neuron:
    # ...
    def neuron_tick(self, inputs):
        # 假设输入和权重都是1xD的向量，偏差是一个数字
        cell_body_sum = np.sum(inputs*self.weights) + self.bias
        # 当和远大于0时，输出为1，被激活
        firing_rate = 1.0 / (1.0 + np.exp(-cell_body_sum))
        return firing_rate

2.3 常用的激活函数

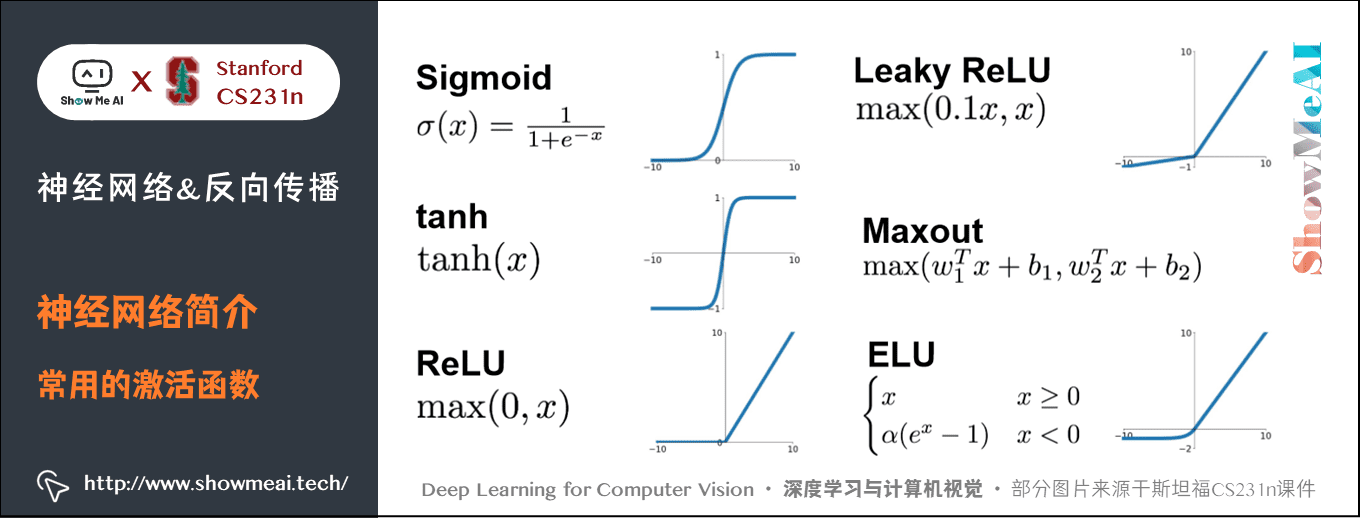
神经网络简介; 常用的激活函数

3.神经网络结构

关于神经网络结构的知识也可以参考ShowMeAI的 深度学习教程 | 吴恩达专项课程 · 全套笔记解读 中的文章 神经网络基础、浅层神经网络、深层神经网络 里对于不同深度的网络结构的讲解

对于普通神经网络，最普通的层级结构是全连接层（fully-connected layer）。全连接层中的神经元与其前后两层的神经元是完全成对连接的，但是在同层内部的神经元之间没有连接。网络结构中没有循环（因为这样会导致前向传播的无限循环）。

下面是两个神经网络的图例，都使用的全连接层：

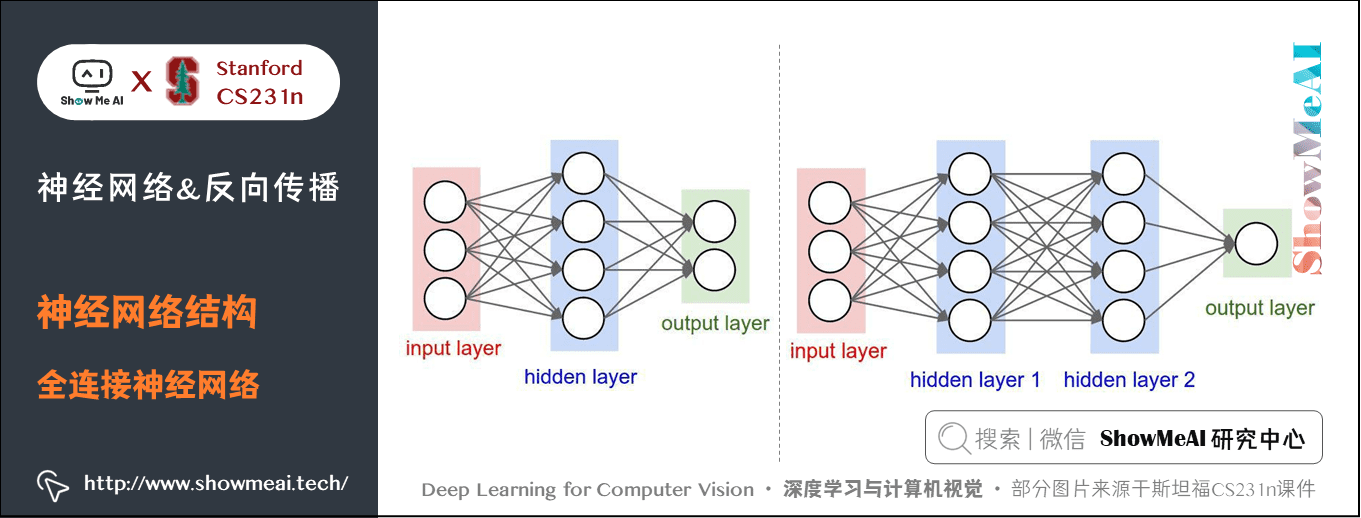
神经网络结构; 全连接神经网络

左边：一个2层神经网络，隐层由4个神经元（也可称为单元（unit））组成，输出层由2个神经元组成，输入层是3个神经元（指的是输入图片的维度而不是图片的数量）。
右边：一个3层神经网络，两个含4个神经元的隐层。

注意：当我们说 $N$ 层神经网络的时候，我们并不计入输入层。单层的神经网络就是没有隐层的（输入直接映射到输出）。也会使用人工神经网络（Artificial Neural Networks 缩写ANN）或者多层感知器（Multi-Layer Perceptrons 缩写MLP）来指代全连接层构建的这种神经网络。此外，输出层的神经元一般不含激活函数。

用来度量神经网络的尺寸的标准主要有两个：一个是神经元的个数，另一个是参数的个数。用上面图示的两个网络举例：

第一个网络有 $4+2=6$ 个神经元（输入层不算），$[3 \times 4]+[4 \times 2]=20$ 个权重，还有$4+2=6$ 个偏置，共 $26$ 个可学习的参数。
第二个网络有 $4+4+1=9$ 个神经元，$[3 \times 4]+[4 \times 4]+[4 \times 1]=32$ 个权重，$4+4+1=9$ 个偏置，共 $41$ 个可学习的参数。

现代卷积神经网络能包含上亿个参数，可由几十上百层构成（这就是深度学习）。

3.1 三层神经网络代码示例

不断用相似的结构堆叠形成网络，这让神经网络算法使用矩阵向量操作变得简单和高效。我们回到上面那个3层神经网络，输入是 $[3 \times 1]$ 的向量。一个层所有连接的权重可以存在一个单独的矩阵中。

比如第一个隐层的权重 $W_1$ 是 $[4 \times 3]$，所有单元的偏置储存在 $b_1$ 中，尺寸 $[4 \times 1]$。这样，每个神经元的权重都在 $W_1$ 的一个行中，于是矩阵乘法 np.dot(W1, x)+b1 就能作为该层中所有神经元激活函数的输入数据。类似的，$W_2$ 将会是 $[4 \times 4]$ 矩阵，存储着第二个隐层的连接，$W_3$ 是 $[1 \times 4]$ 的矩阵，用于输出层。

完整的3层神经网络的前向传播就是简单的3次矩阵乘法，其中交织着激活函数的应用。

import numpy as np

# 三层神经网络的前向传播
# 激活函数
f = lambda x: 1.0/(1.0 + np.exp(-x))

# 随机输入向量3x1
x = np.random.randn(3, 1)
# 设置权重和偏差
W1, W2, W3 = np.random.randn(4, 3), np.random.randn(4, 4), np.random.randn(1, 4),
b1, b2= np.random.randn(4, 1), np.random.randn(4, 1)
b3 = 1

# 计算第一个隐藏层激活 4x1
h1 = f(np.dot(W1, x) + b1)
# 计算第二个隐藏层激活 4x1
h2 = f(np.dot(W2, h1) + b2)
# 输出是一个数
out = np.dot(W3, h2) + b3

在上面的代码中，$W_1$，$W_2$，$W_3$，$b_1$，$b_2$，$b_3$ 都是网络中可以学习的参数。注意 $x$ 并不是一个单独的列向量，而可以是一个批量的训练数据（其中每个输入样本将会是 $x$ 中的一列），所有的样本将会被并行化的高效计算出来。

注意神经网络最后一层通常是没有激活函数的（例如，在分类任务中它给出一个实数值的分类评分）。

全连接层的前向传播一般就是先进行一个矩阵乘法，然后加上偏置并运用激活函数。

3.2 理解神经网络

关于深度神经网络的解释也可以参考ShowMeAI的 深度学习教程 | 吴恩达专项课程 · 全套笔记解读 中的文章 深层神经网络 里「深度网络其他优势」部分的讲解

全连接层的神经网络的一种理解是：

它们定义了一个由一系列函数组成的函数族，网络的权重就是每个函数的参数。

拥有至少一个隐层的神经网络是一个通用的近似器，神经网络可以近似任何连续函数。

虽然一个2层网络在数学理论上能完美地近似所有连续函数，但在实际操作中效果相对较差。虽然在理论上深层网络（使用了多个隐层）和单层网络的表达能力是一样的，但是就实践经验而言，深度网络效果比单层网络好。

对于全连接神经网络而言，在实践中3层的神经网络会比2层的表现好，然而继续加深（做到4，5，6层）很少有太大帮助。卷积神经网络的情况却不同，在卷积神经网络中，对于一个良好的识别系统来说，深度是一个非常重要的因素（比如当今效果好的CNN都有几十上百层）。对于该现象的一种解释观点是：因为图像拥有层次化结构（比如脸是由眼睛等组成，眼睛又是由边缘组成），所以多层处理对于这种数据就有直观意义。

4.拓展学习

可以点击 B站查看视频的【双语字幕】版本

5.要点总结

前向传播与反向传播
标量与向量化形式计算
求导链式法则应用
神经网络结构
激活函数
理解神经网络

斯坦福 CS231n 全套解读

ShowMeAI 系列教程推荐

ShowMeAI用知识加速每一次技术成长

posted @ 2022-05-30 00:40 ShowMeAI 阅读(343) 评论(0) 编辑收藏举报

刷新页面返回顶部

ShowMeAI

『为AI硬核资料库(cool)而生！』构建AI解决方案，用知识加速每一次技术成长！公众号：ShowMeAI研究中心