斯坦福NLP课程 | 第4讲 - 神经网络反向传播与计算图

ShowMeAI研究中心

神经网络反向传播与计算图
ShowMeAI为斯坦福CS224n《自然语言处理与深度学习(Natural Language Processing with Deep Learning)》课程的全部课件，做了中文翻译和注释，并制作成了GIF动图！

神经网络与反向传播
本讲内容的深度总结教程可以在这里 查看。视频和课件等资料的获取方式见文末。

引言

Backpropagation and Computation Graphs

内容覆盖

Backpropagation and Computation Graphs

  • ① 简单神经网络的梯度矩阵与建议
  • ② 计算图与反向传播
  • ③ 神经网络训练实用知识技能
    • 正则化（用于环节过拟合）
    • 向量化
    • 非线性表达能力
    • 参数初始化
    • 优化算法
    • 学习率策略

1.简单神经网络的梯度矩阵与建议

1.1 权重矩阵的导数

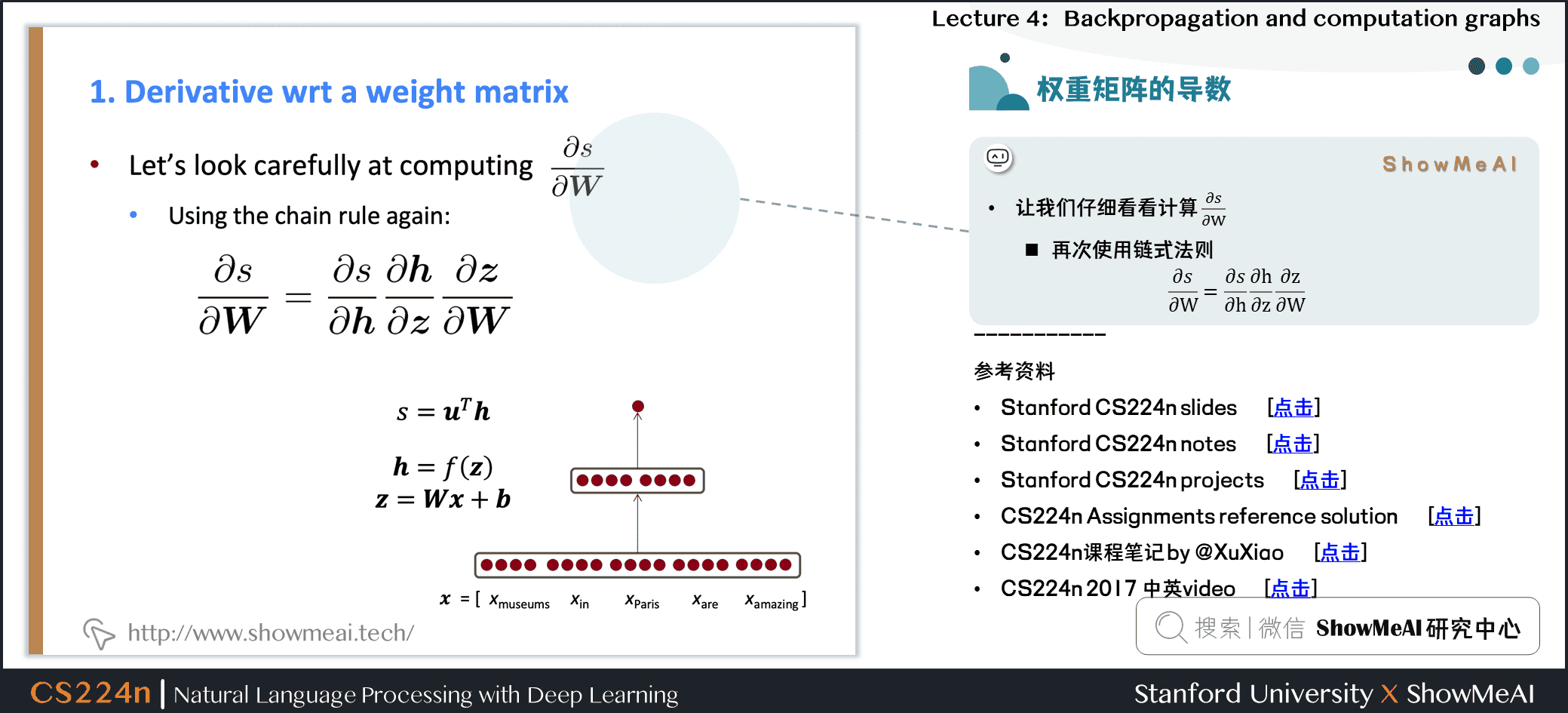
权重矩阵的导数

  • 让我们仔细看看计算 \(\frac{\partial s}{\partial W}\)
    • 再次使用链式法则

\[\frac{\partial s}{\partial W}=\frac{\partial s}{\partial h} \frac{\partial h}{\partial z} \frac{\partial z}{\partial W} \]

\[\begin{aligned} s &= u^T h \\ h &= f(z) \\ z &= Wx+b \end{aligned} \]

1.2 反向传播梯度求导

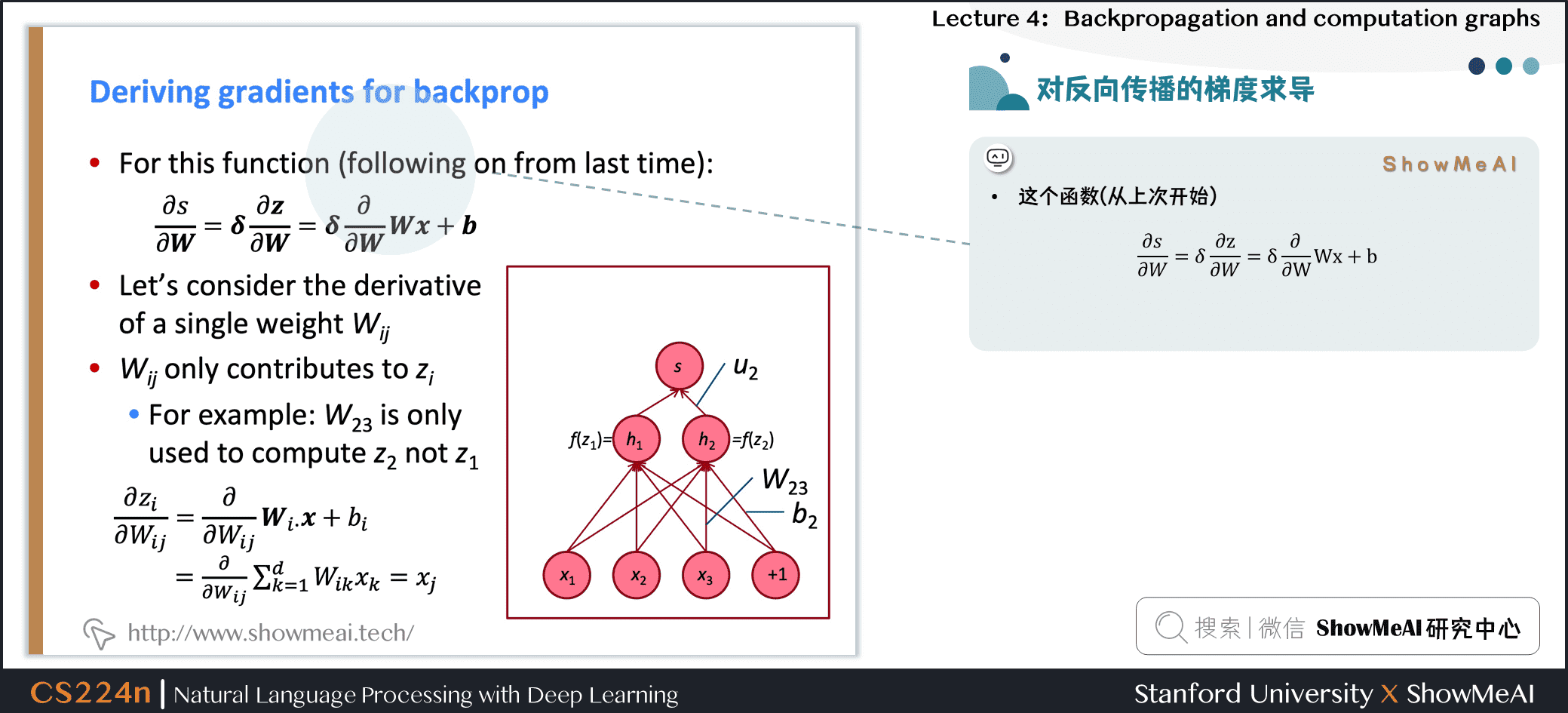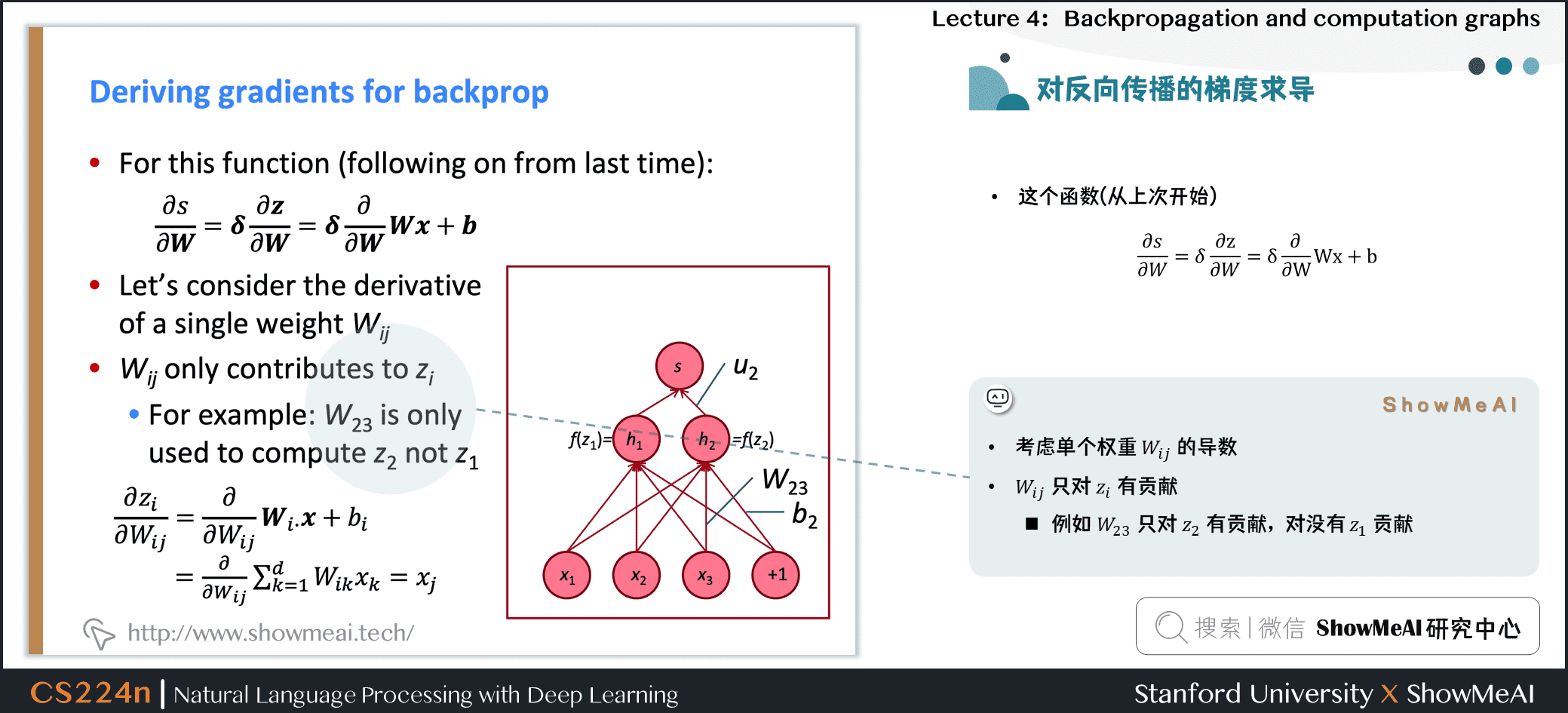
对反向传播的梯度求导

  • 这个函数(从上次开始)

\[\frac{\partial s}{\partial W}=\delta \frac{\partial z}{\partial W}=\delta \frac{\partial}{\partial W} Wx+b \]

  • 考虑单个权重 \(W_{ij}\) 的导数
  • \(W_{ij}\) 只对 \(z_i\) 有贡献
    • 例如 \(W_{23}\) 只对 \(z_2\) 有贡献，对 \(z_1\) 没有贡献

\[\begin{aligned} \frac{\partial z_{i}}{\partial W_{i j}} &=\frac{\partial}{\partial W_{i j}} W_{i \cdot} x+b_{i} \\ &=\frac{\partial}{\partial W_{i j}} \sum_{k=1}^{d} W_{i k} x_{k}=x_{j} \end{aligned} \]

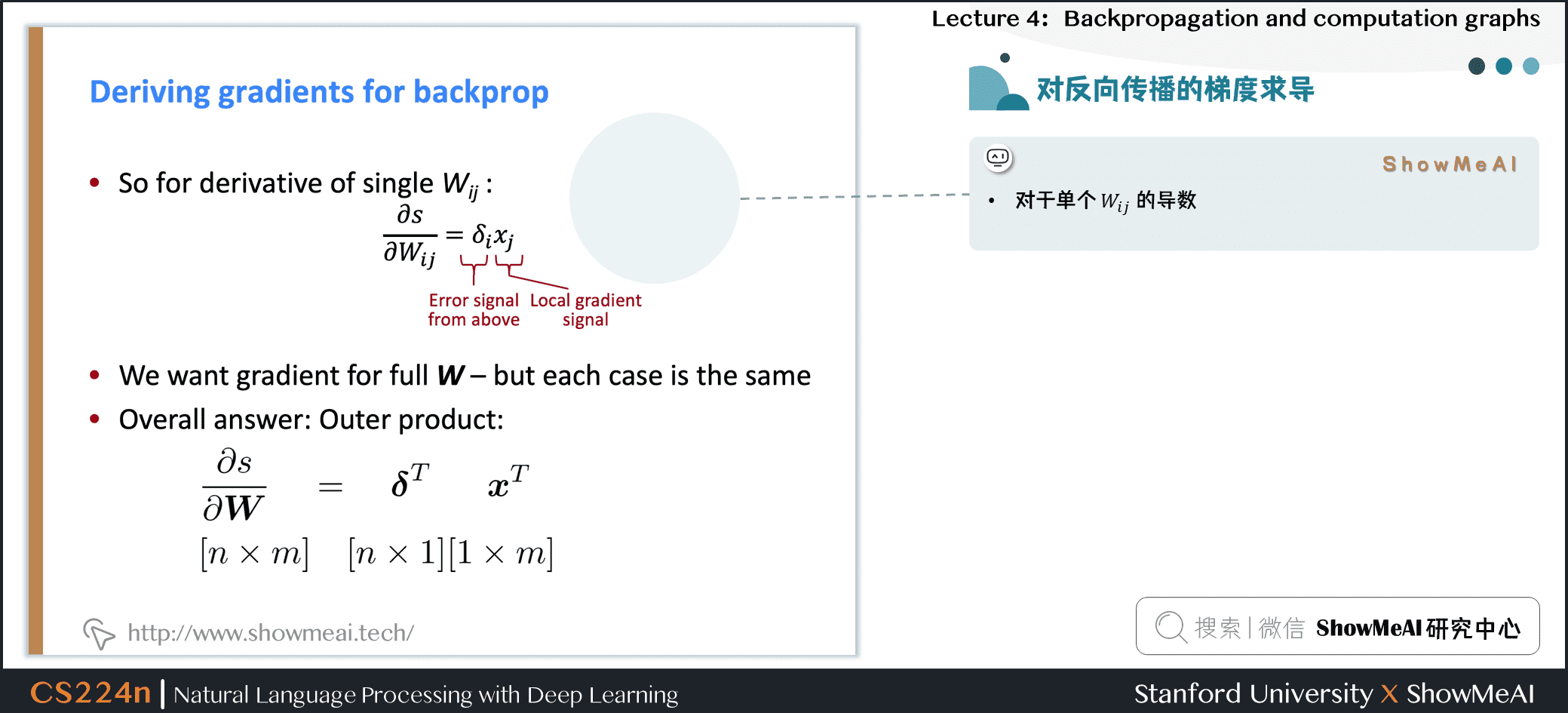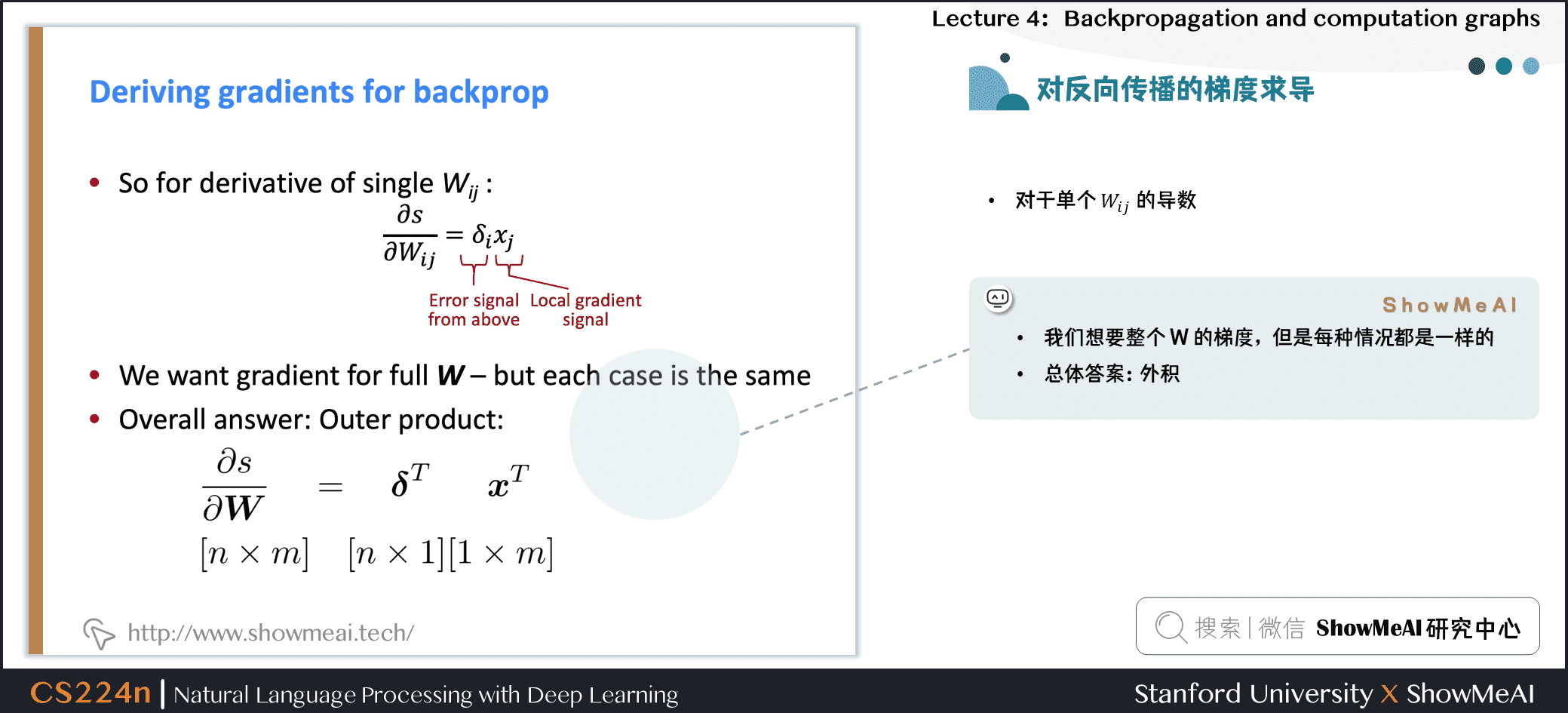
对反向传播的梯度求导

  • 对于单个 \(W_{ij}\) 的导数：

\[\frac{\partial s}{\partial W_{i j}} = \delta_i x_j \]

  • 我们想要整个 \(W\) 的梯度，但是每种情况都是一样的
  • 解决方案：外积

\[\begin{aligned} \frac{\partial s}{\partial {W}}&=\delta ^{T} x^{T}\\ [n \times m] &= [n \times 1][1 \times m] \end{aligned} \]

1.3 梯度求导：技巧与建议

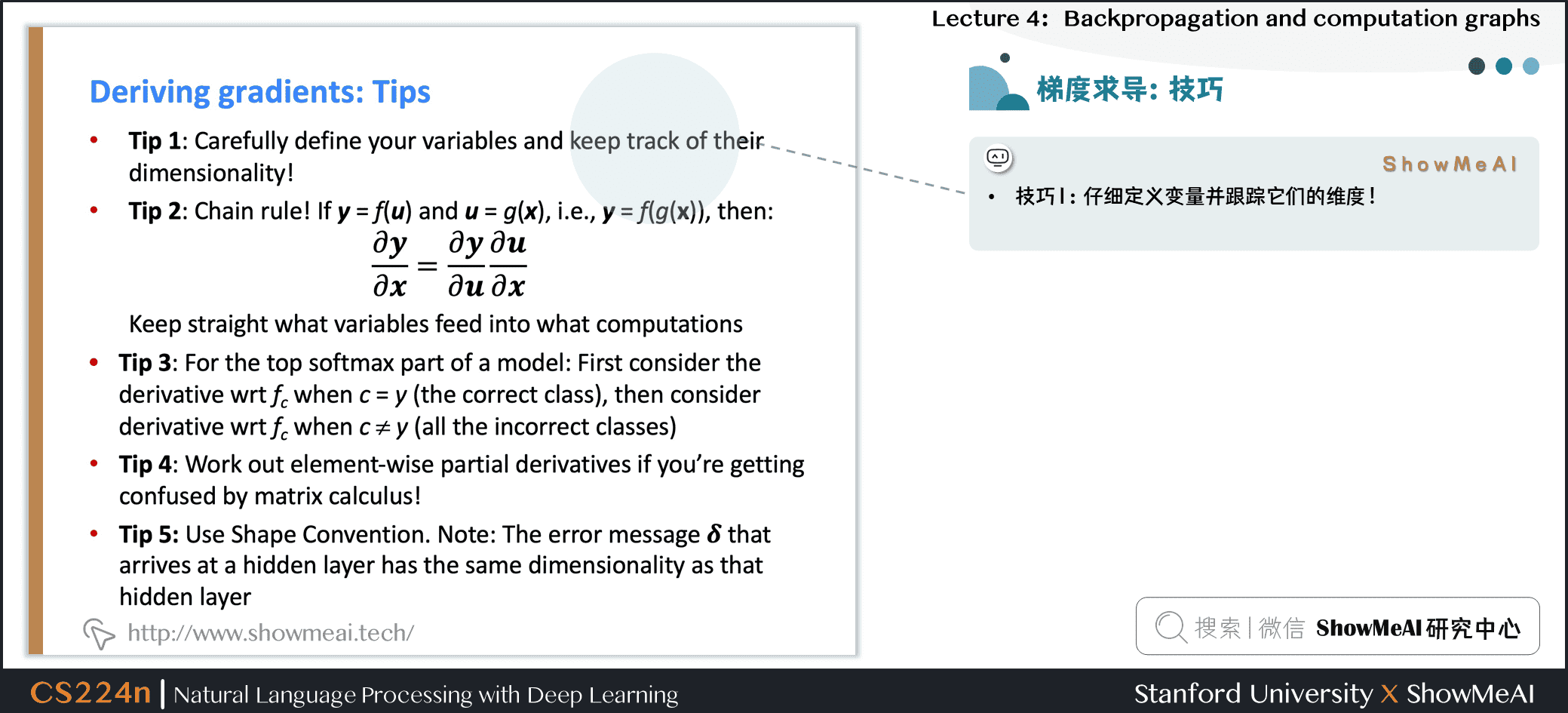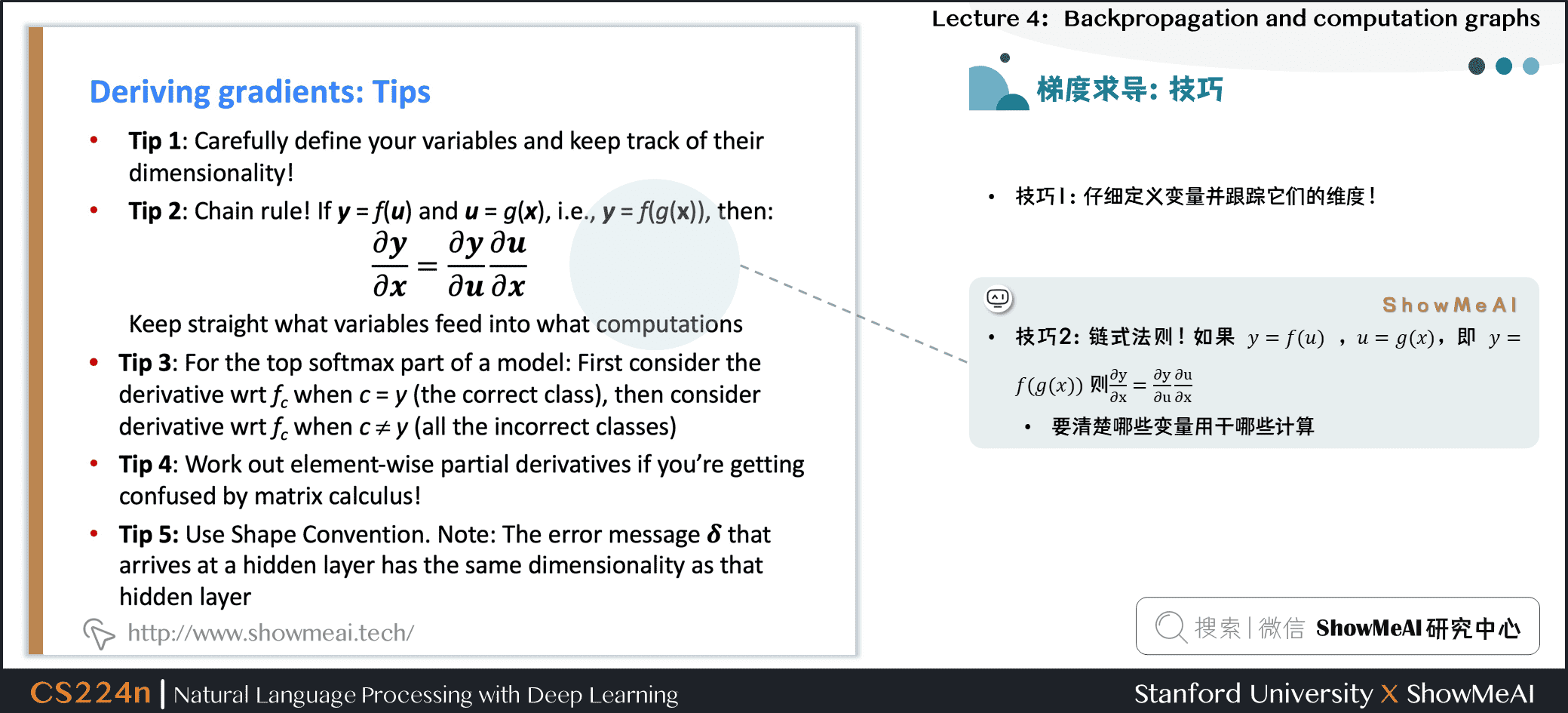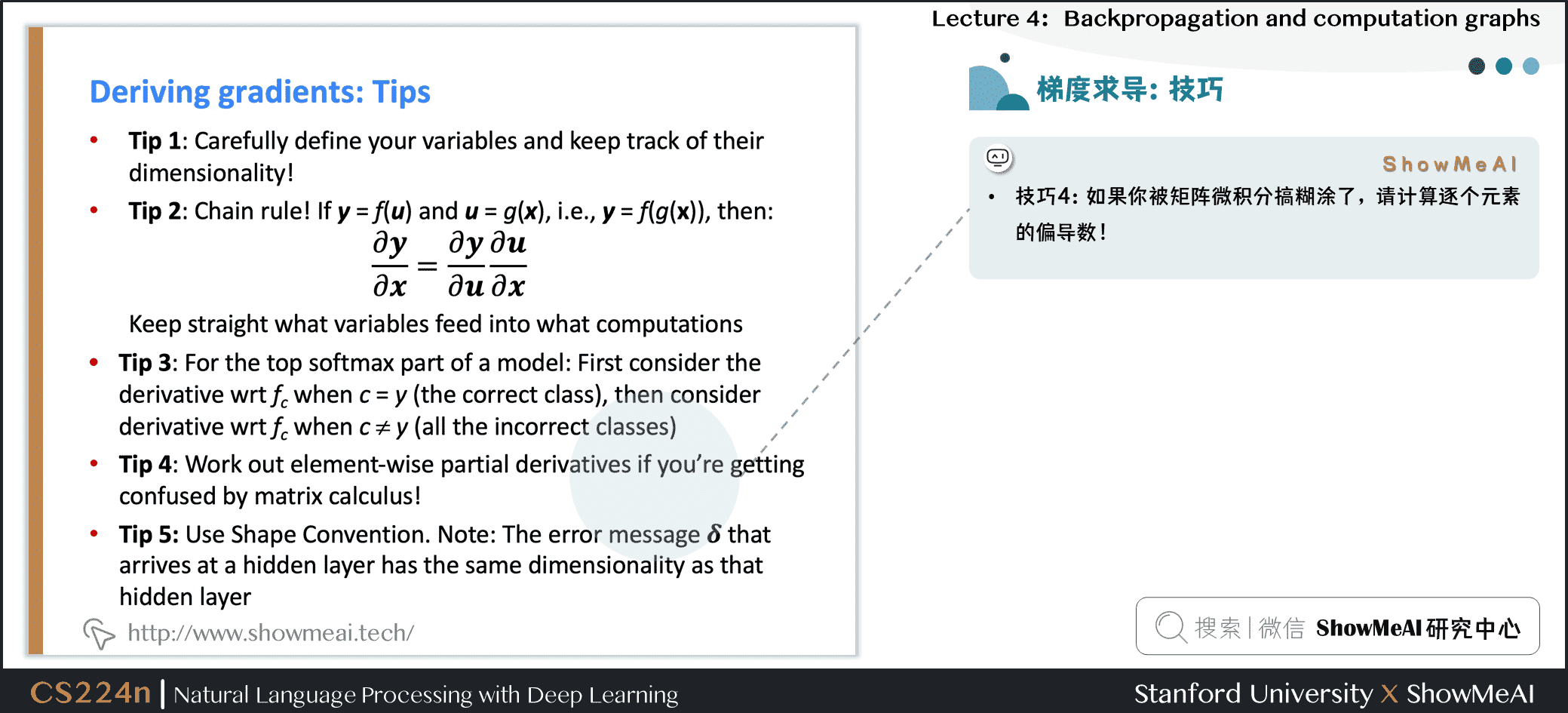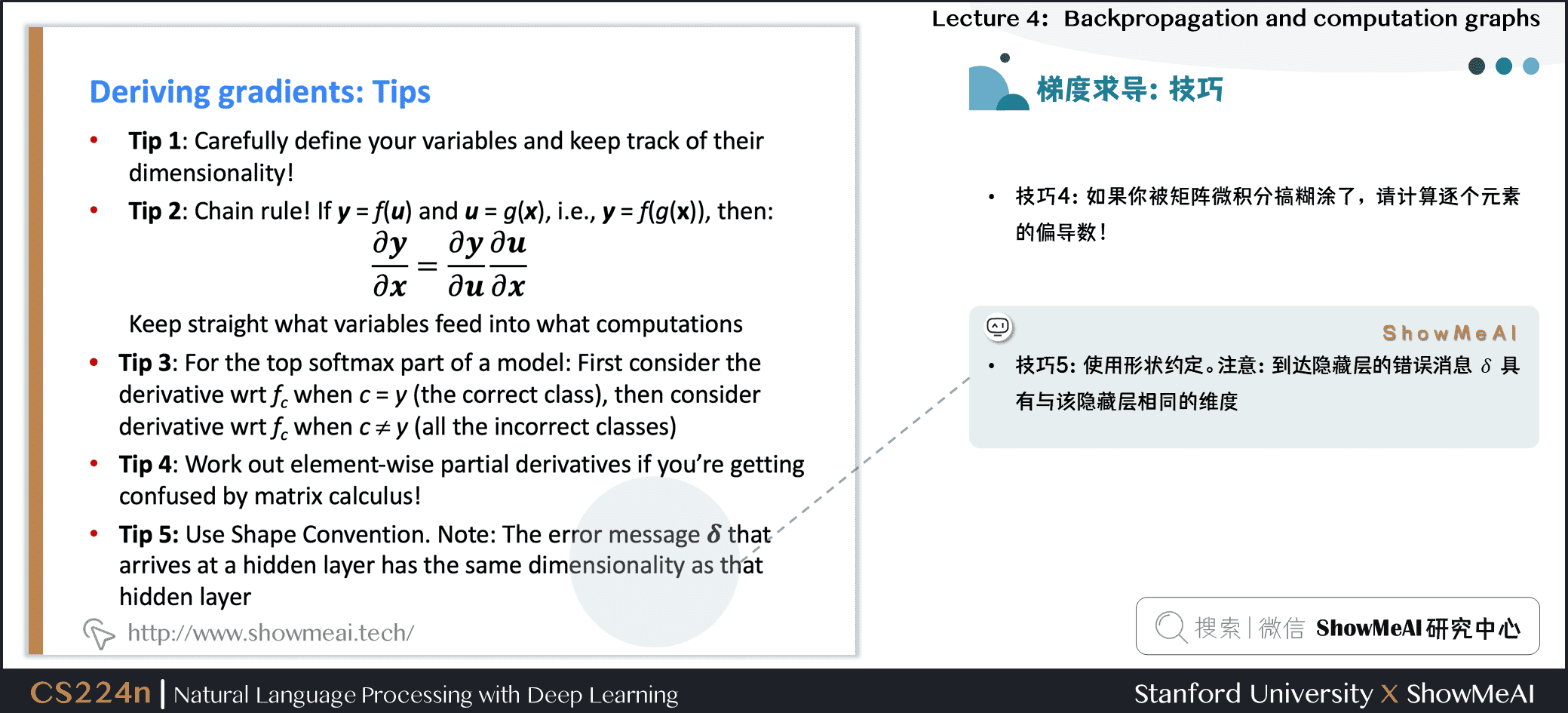
梯度求导：技巧

  • 技巧1：仔细定义变量并关注它们的维度！

  • 技巧2：链式法则！如果 \(y = f(u)\) , \(u = g(x)\)，即 \(y = f(g(x))\) 则

\[\frac{\partial {y}}{\partial {x}}=\frac{\partial {y}}{\partial {u}} \frac{\partial {u}}{\partial {x}} \]

  • 提示3：模型的最上面的softmax部分：首先考虑当 \(c = y\) (正确的类)的导数 \(f_c\)，然后再考虑当 \(c \neq y\) (所有不正确的类)的导数 \(f_c\)

  • 技巧4：如果你被矩阵微积分搞糊涂了，请计算逐个元素的偏导数！

  • 技巧5：使用形状约定。注意：到达隐藏层的错误消息 \(\delta\) 具有与该隐藏层相同的维度

1.4 为窗口模型推导梯度

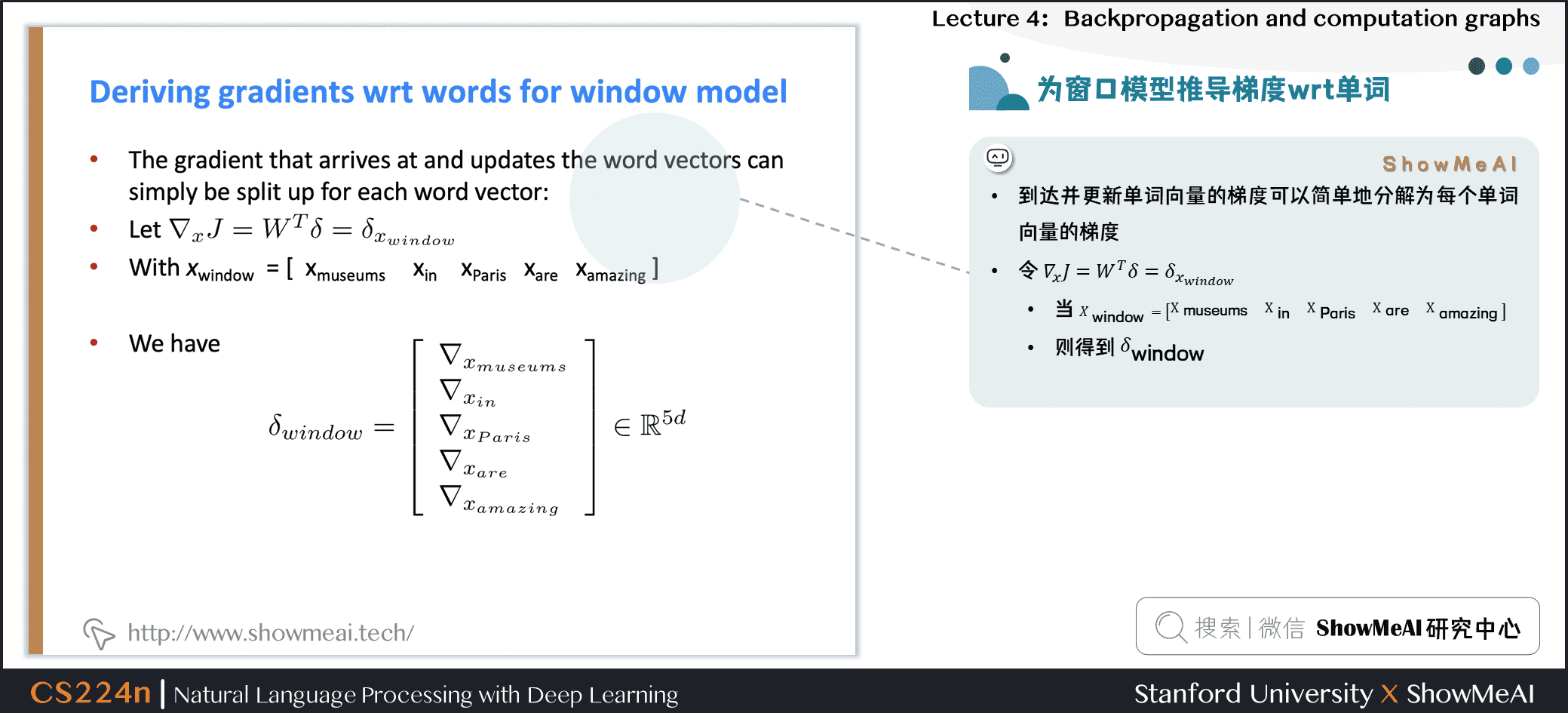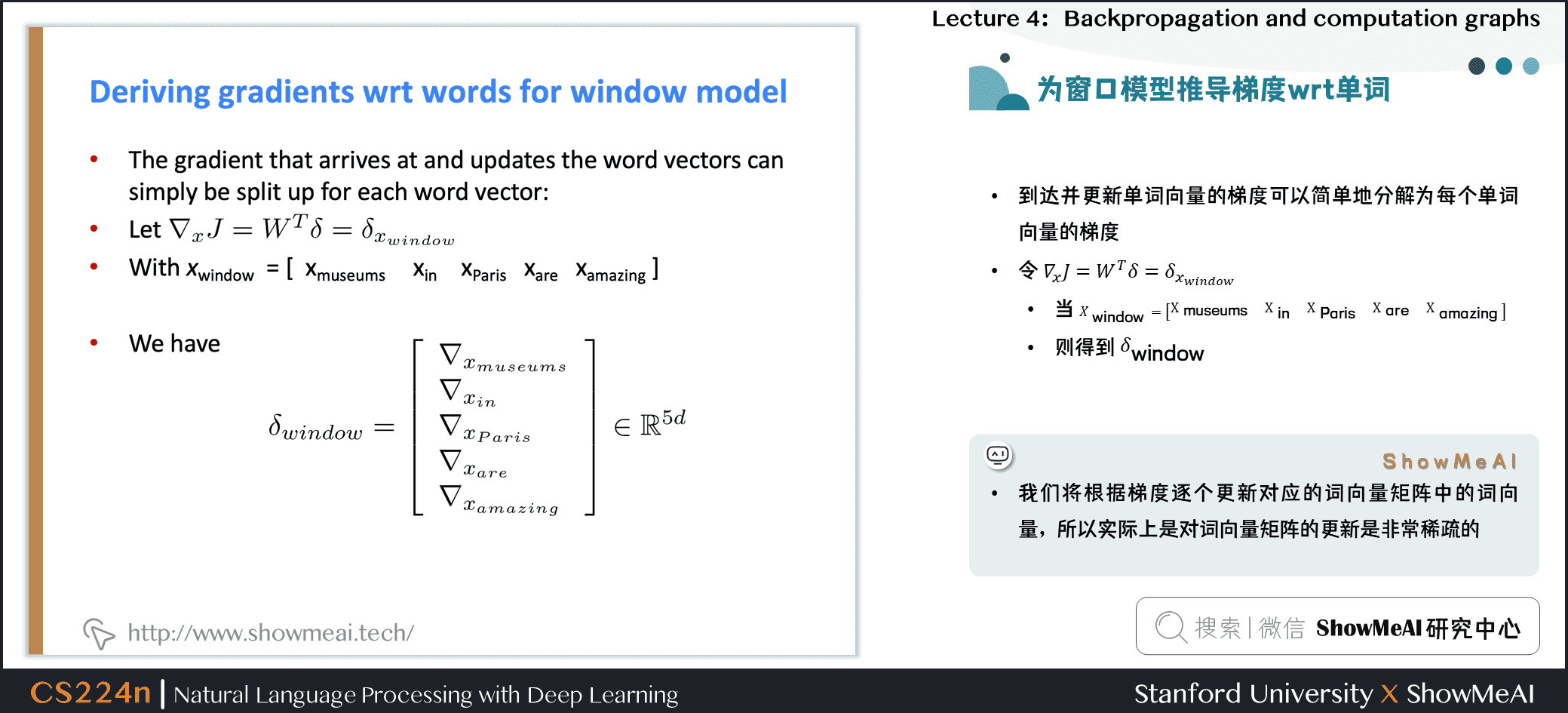
为窗口模型推导梯度wrt单词

  • 到达并更新单词向量的梯度可以简单地分解为每个单词向量的梯度

  • 令 \(\nabla_{x} J=W^{T} \delta=\delta_{x_{w i n d o w}}\)

  • \(X_{window}=[X_{museums} \quad X_{in} \quad X_{Paris} \quad X_{are} \quad X_{ amazing}]\)

  • 则得到

\[\begin{aligned} \delta_{window}=\left[\begin{array}{c}{\nabla_{x_{\text {museums}}}} \\ {\nabla_{x_{i n}}} \\ {\nabla_{x_{\text {Pare}}}} \\ {\nabla_{x_{\text {are}}}} \\ {\nabla_{x_{\text {amazing}}}}\end{array}\right] \in \mathbb{R}^{5 d} \end{aligned} \]

  • 我们将根据梯度逐个更新对应的词向量矩阵中的词向量，所以实际上是对词向量矩阵的更新是非常稀疏的

1.5 在窗口模型中更新单词梯度

在窗口模型中更新单词梯度

  • 当我们将梯度更新到词向量中时，这将更新单词向量，使它们(理论上)在确定命名实体时更有帮助。
  • 例如，模型可以了解到，当看到 \(x_{in}\) 是中心词之前的单词时，指示中心词是一个 Location

1.6 重新训练词向量时的陷阱

重新训练词向量时的陷阱

背景：我们正在训练一个单词电影评论情绪的逻辑回归分类模型。

  • 在训练数据中，我们有“TV”和“telly”
  • 在测试数据中我们有“television””
  • 预训练的单词向量有三个相似之处：

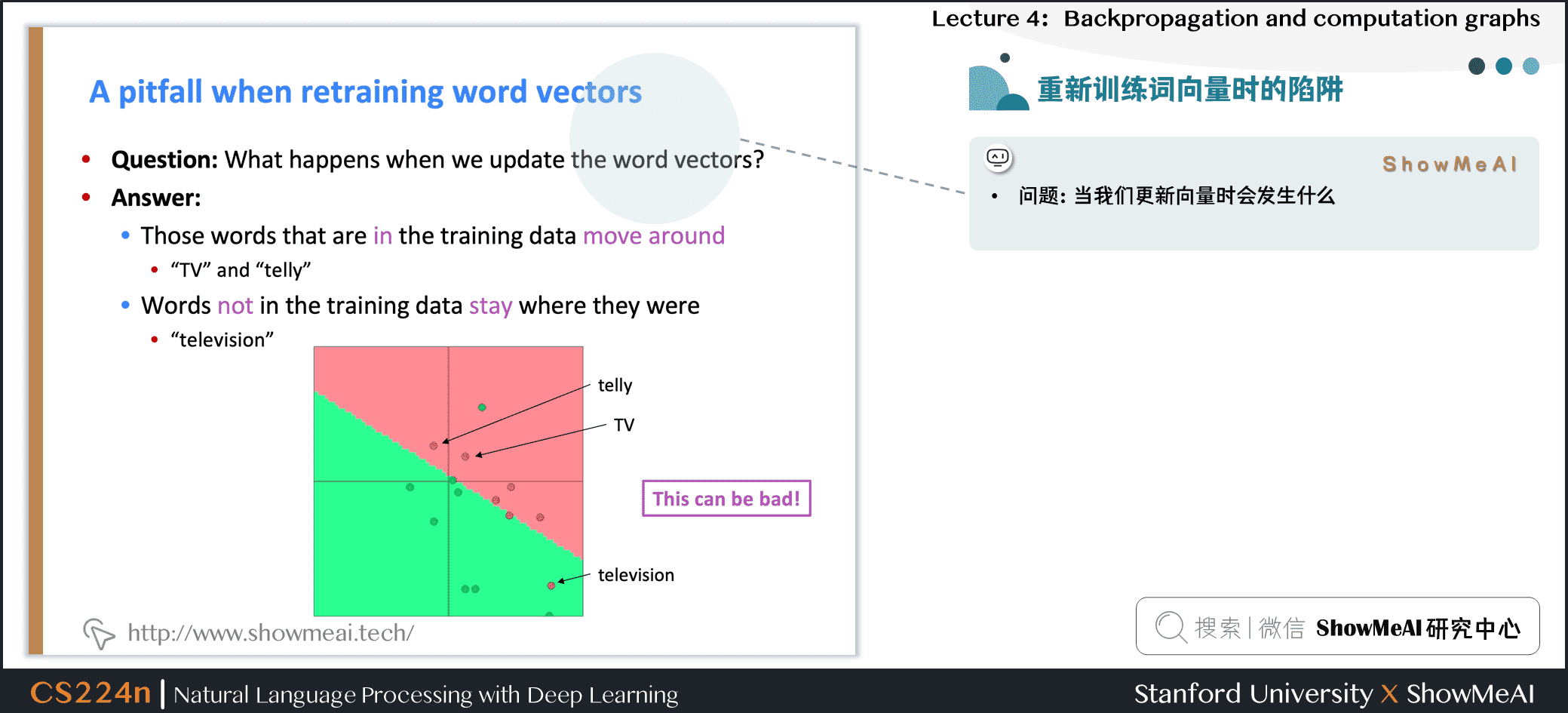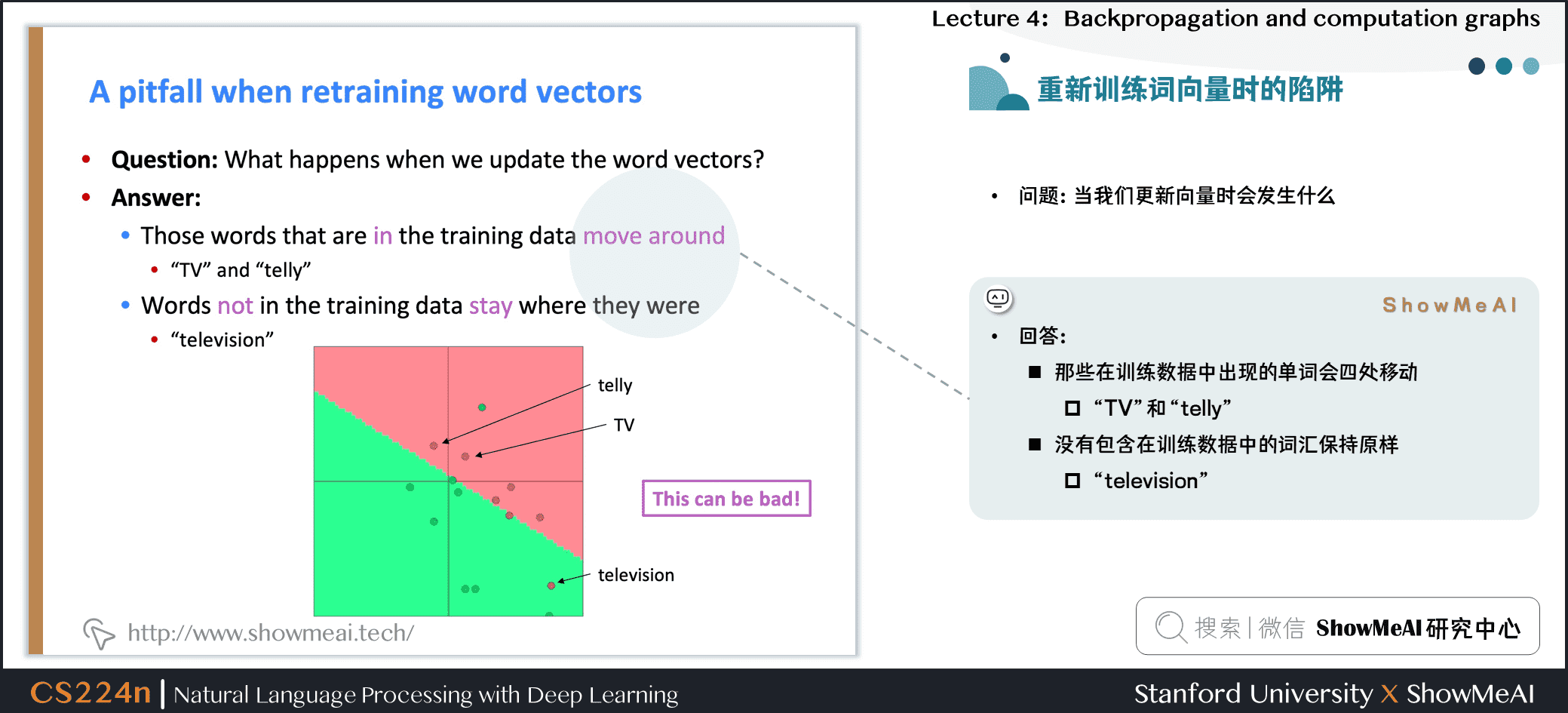
重新训练词向量时的陷阱

  • 问题：当我们更新向量时会发生什么

  • 回答：

    • 那些在训练数据中出现的单词会四处移动
      • “TV”和“telly”
    • 没有包含在训练数据中的词汇保持原样
      • “television”

1.7 关于再训练的建议

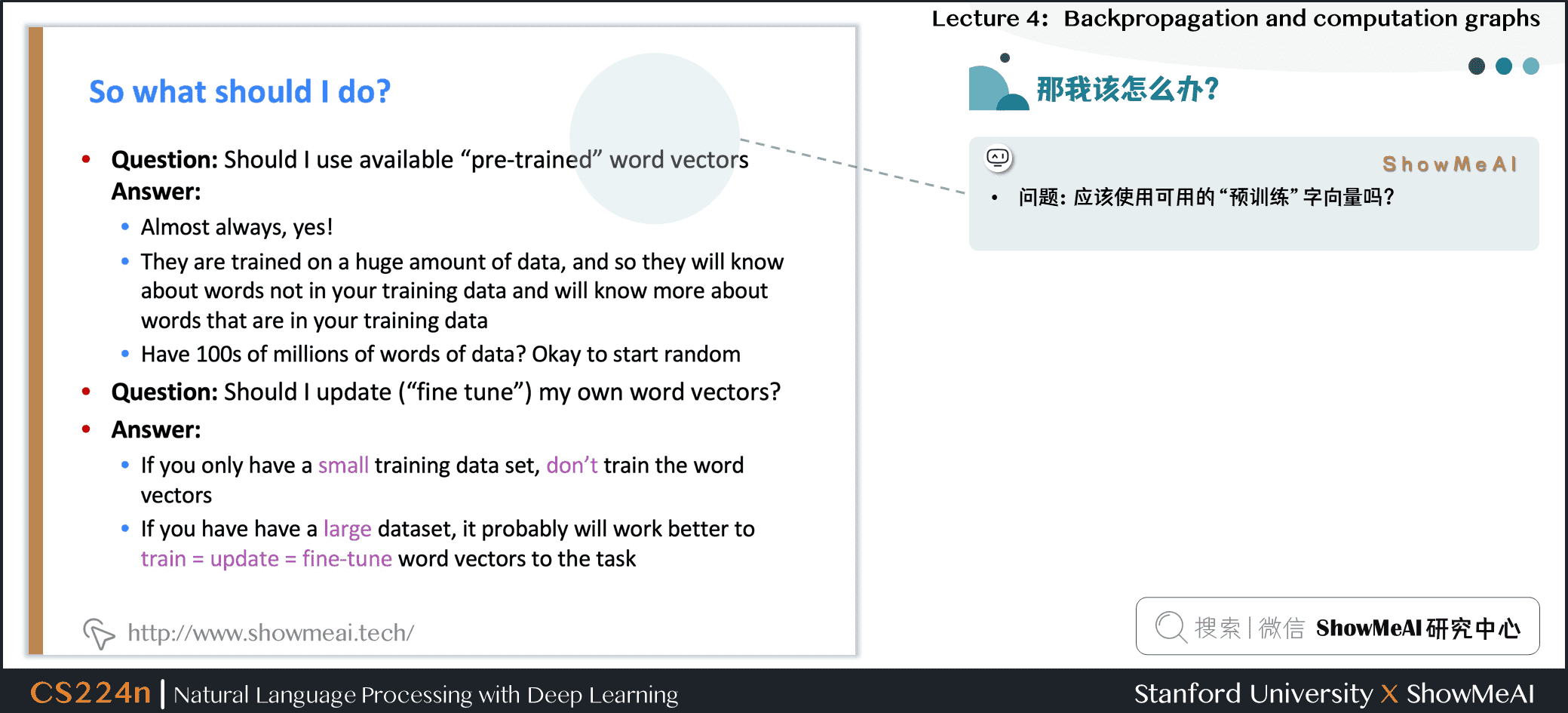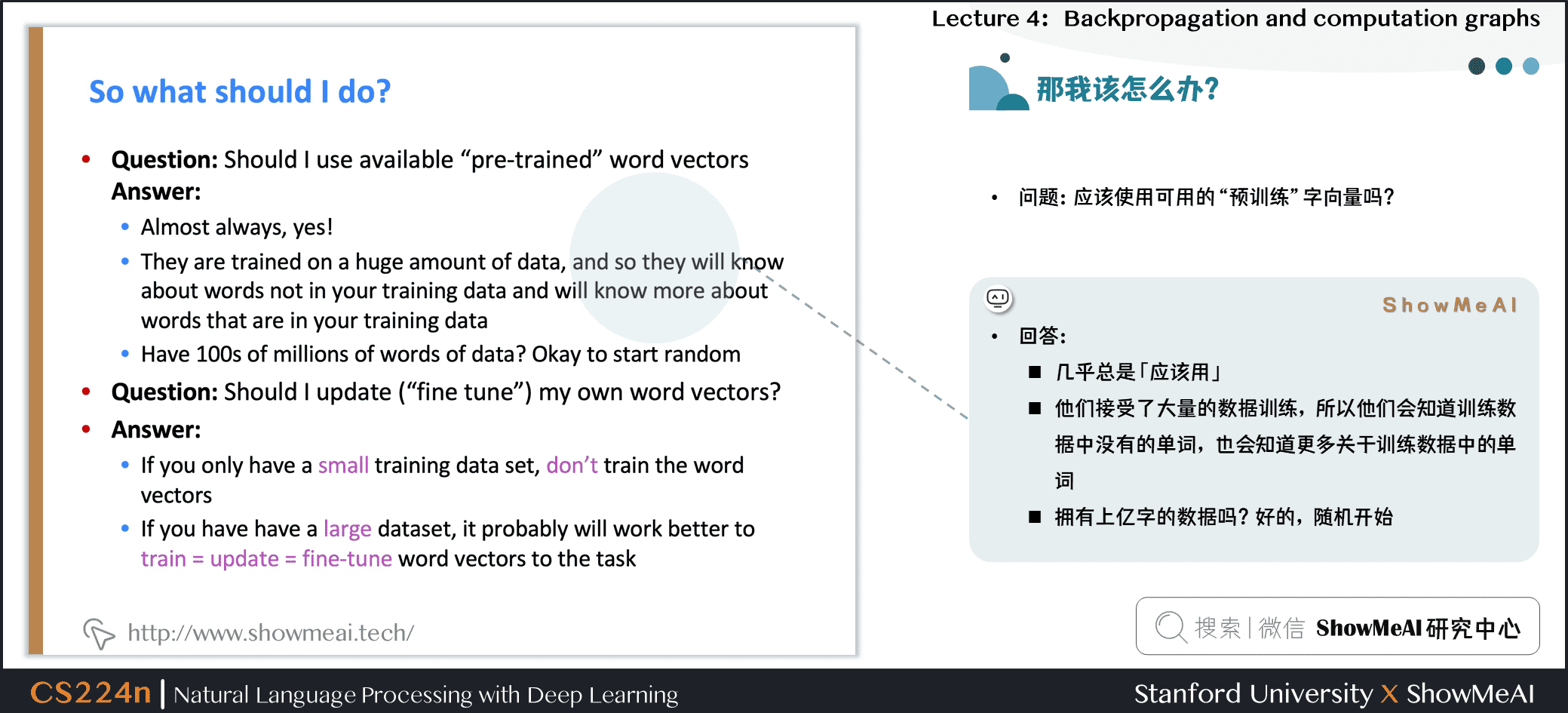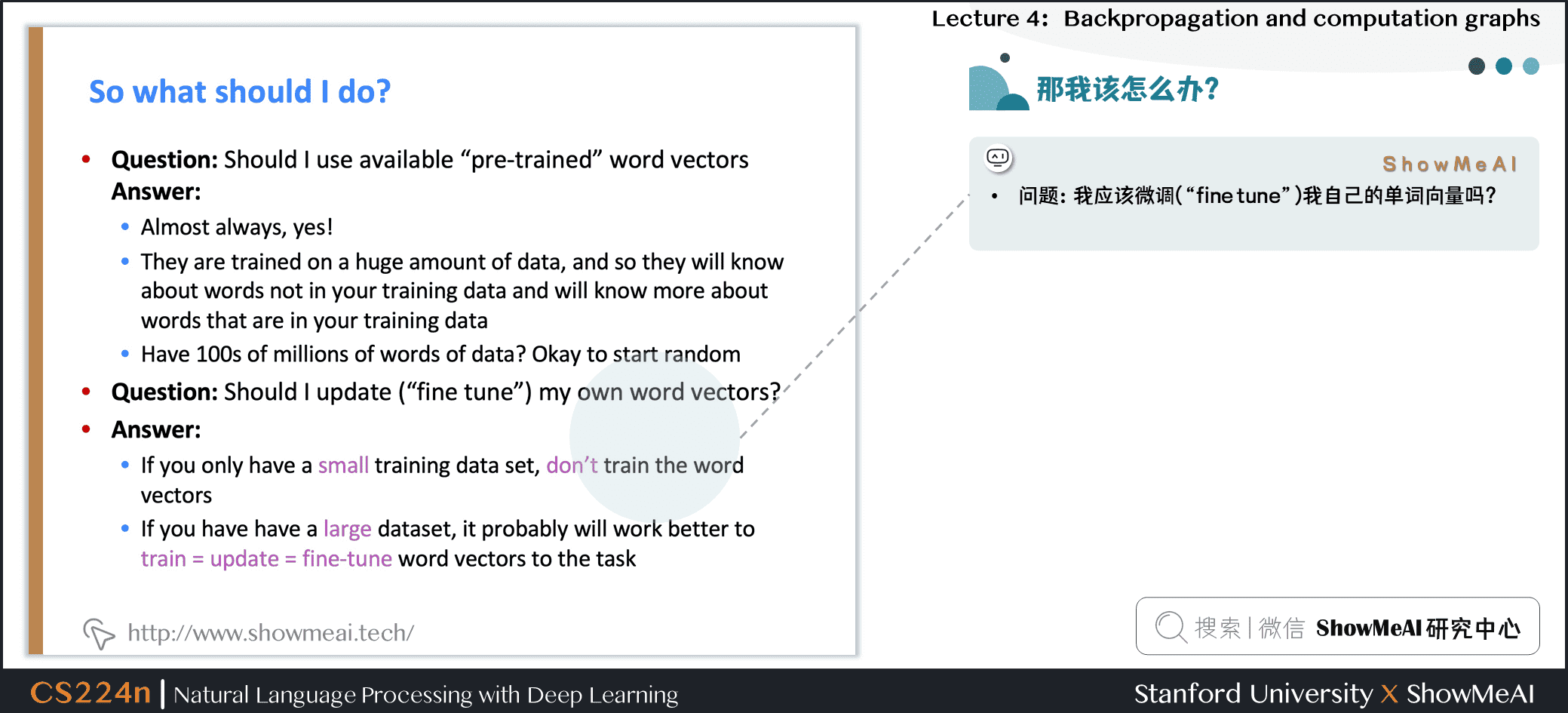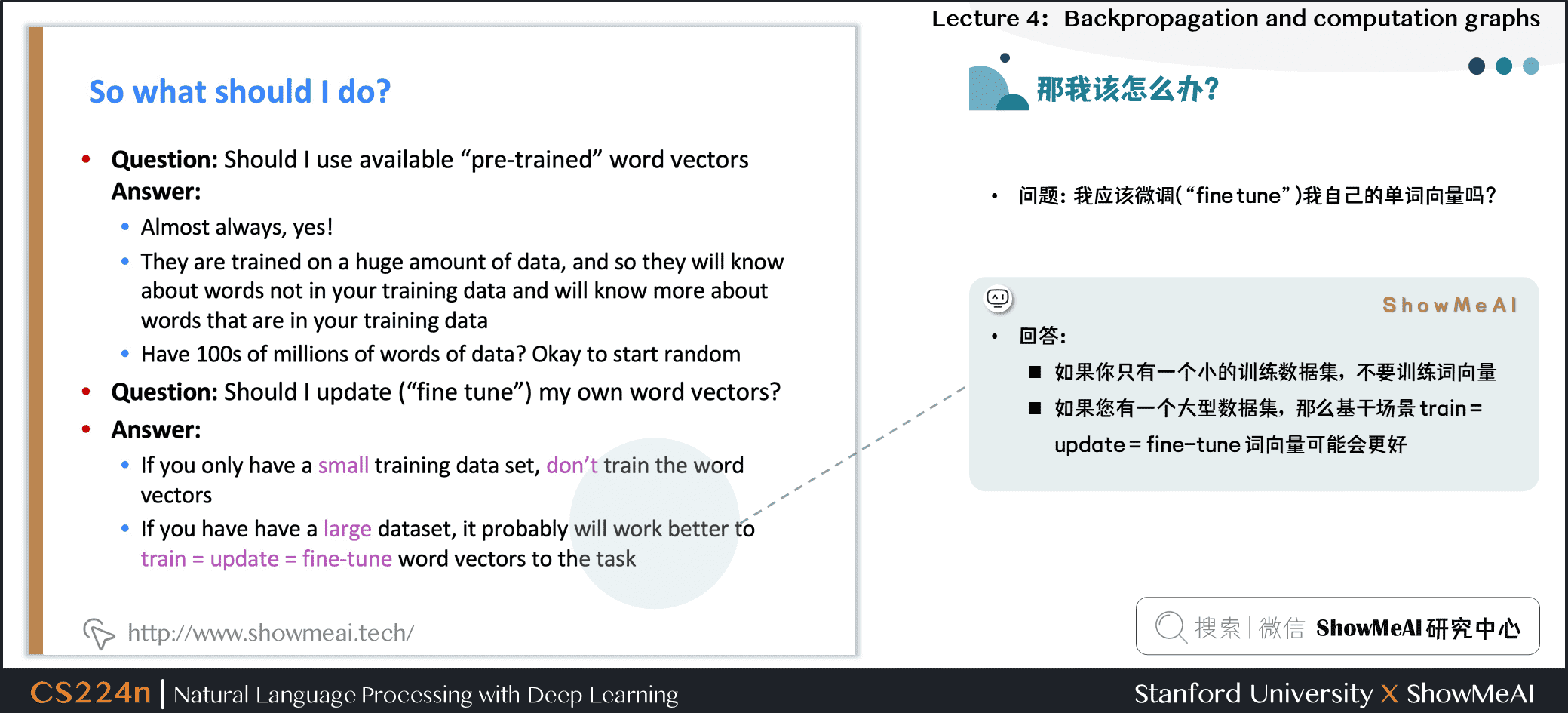
关于“词向量”再训练的建议

  • 问题：应该使用可用的“预训练”词向量吗？

  • 回答：

    • 几乎总是「应该用」
    • 他们接受了大量的数据训练，所以他们会知道训练数据中没有的单词，也会知道更多关于训练数据中的单词
    • 拥有上亿的数据语料吗？那可以随机初始化开始训练

  • 问题：我应该更新(“fine tune”)我自己的单词向量吗？

  • 回答：

    • 如果你只有一个小的训练数据集，不要对预训练词向量做再训练
    • 如果您有一个大型数据集，那么基于任务训练更新词向量（ train = update = fine-tune ）效果会更好

2.计算图与反向传播

2.1 反向传播

反向传播

  • 我们几乎已经向你们展示了反向传播

    • 求导并使用(广义)链式法则

  • 另一个技巧：在计算较低层的导数时，我们重用对较深层计算的导数，以减小计算量

2.2 计算图和反向传播

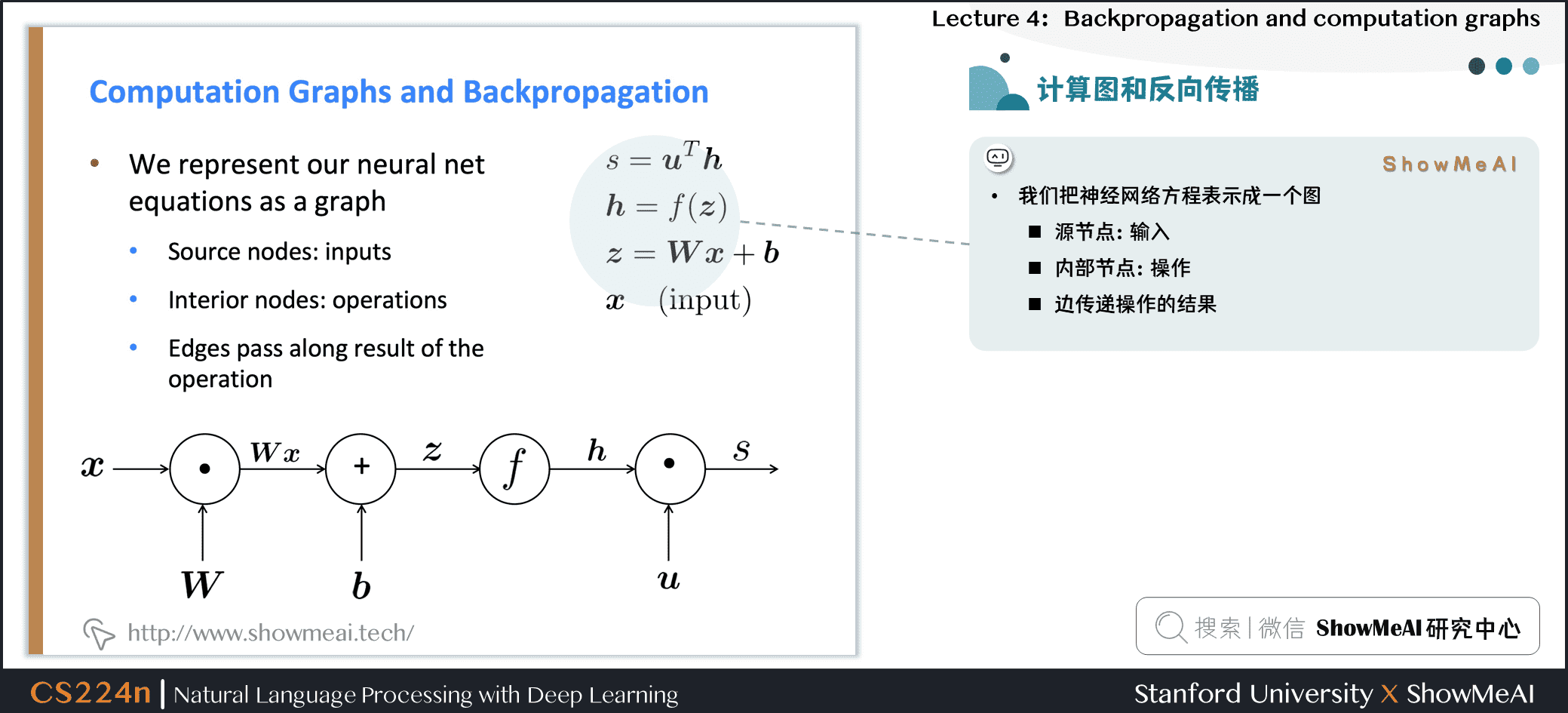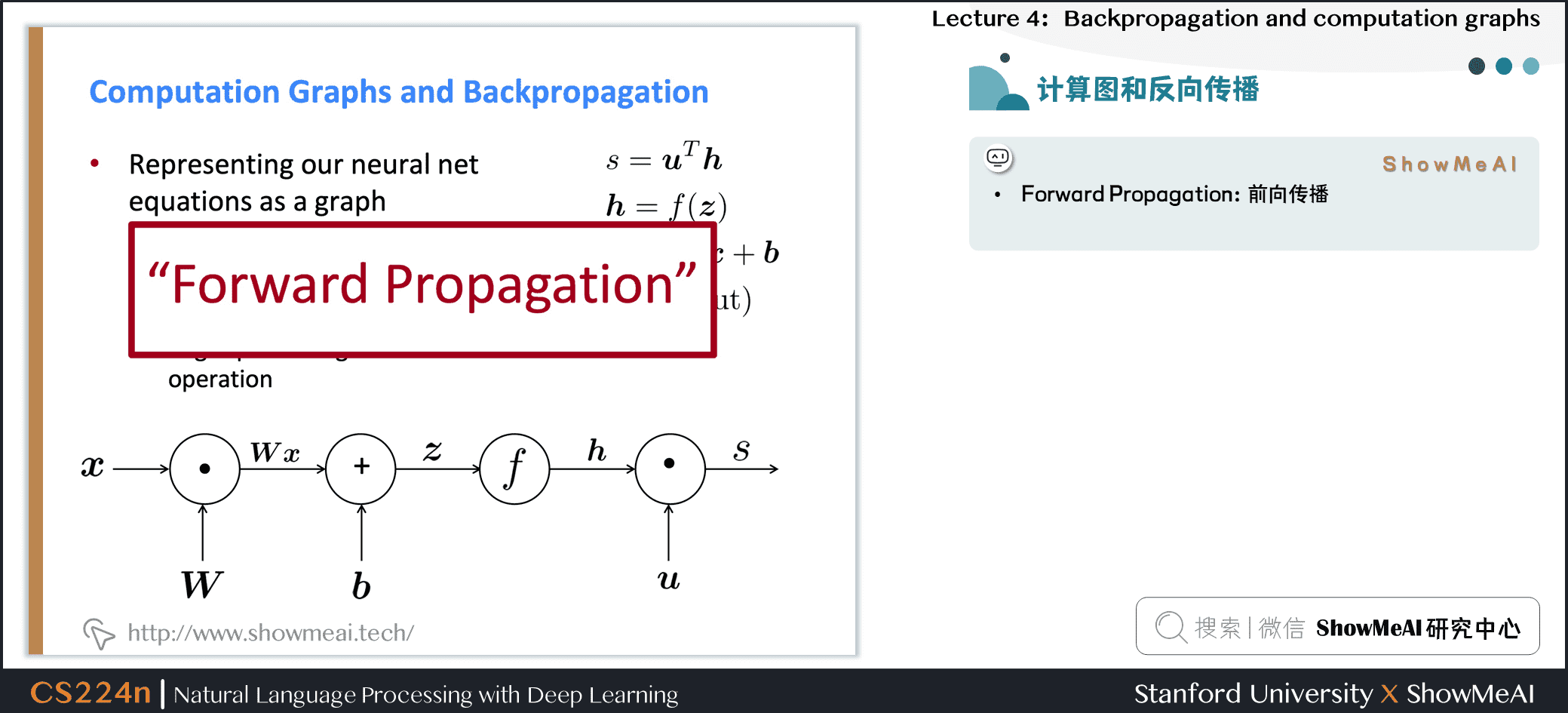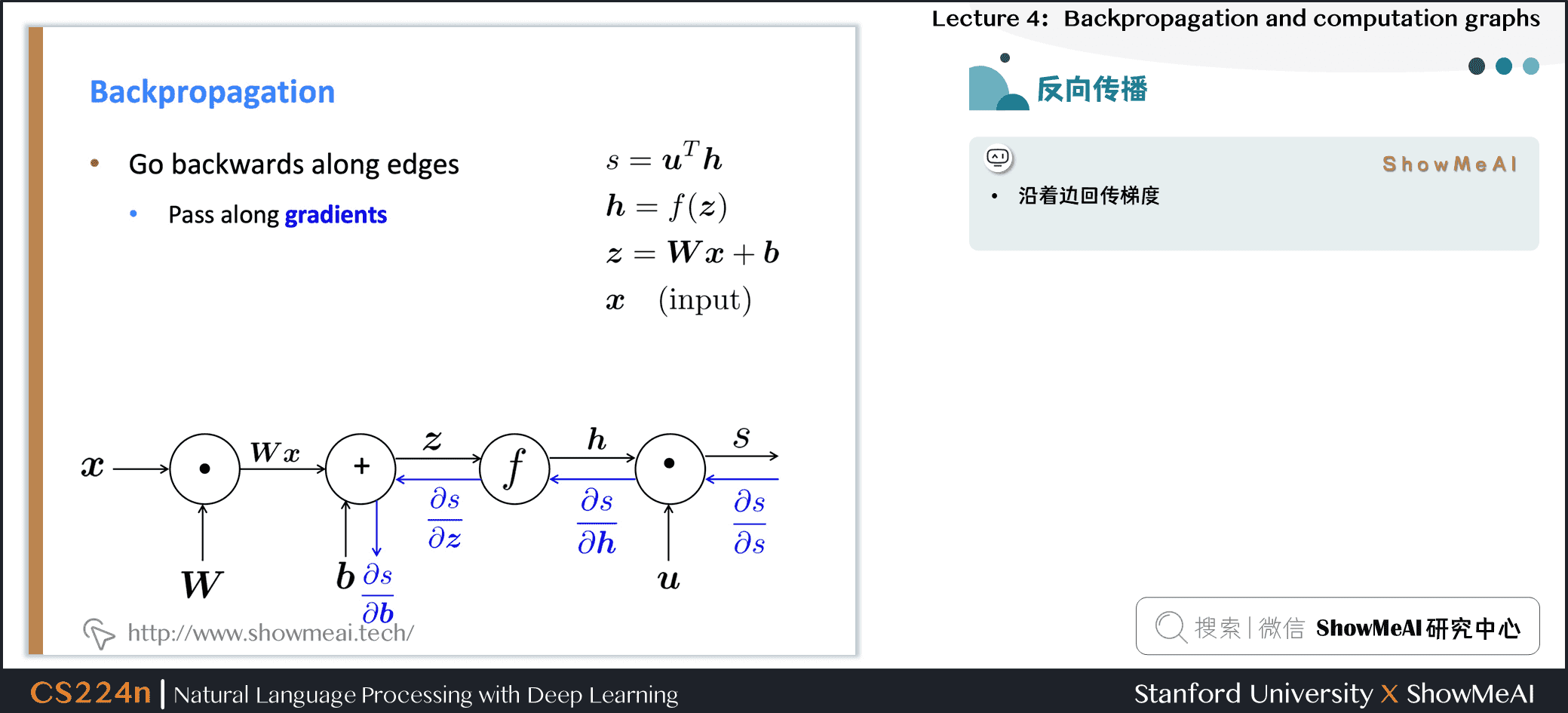
计算图和反向传播

  • 我们把神经网络方程表示成一个图
    • 源节点：输入
    • 内部节点：操作
    • 边传递操作的结果

\[\begin{aligned} s &= u^Th \\ h &= f(z) \\ z &= Wx+b \\ x & \quad (input) \end{aligned} \]

Forward Propagation：前向传播
Back Propagation：沿着边回传梯度

2.3 反向传播：单神经元视角

反向传播：单神经元视角

  • 节点接收“上游梯度”

    • 目标是传递正确的“下游梯度”

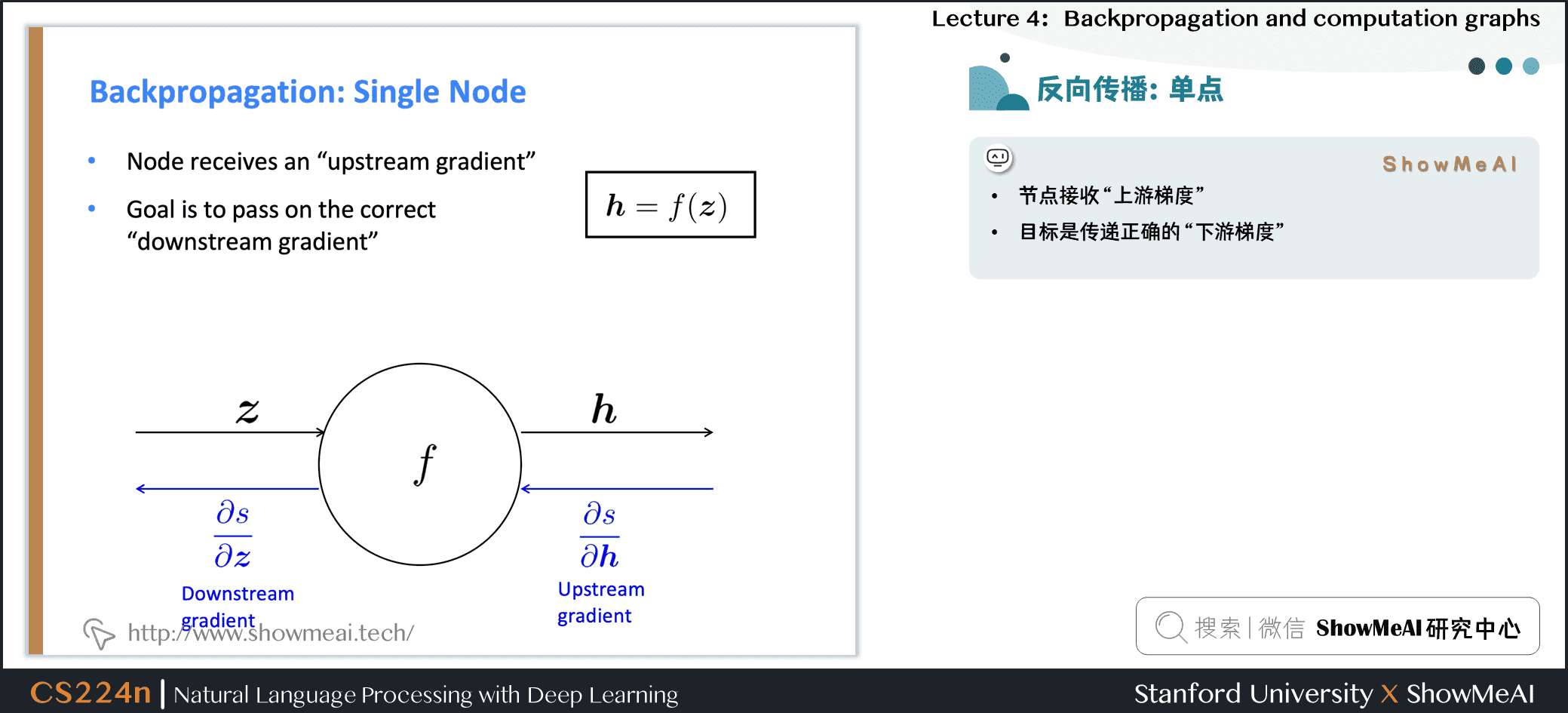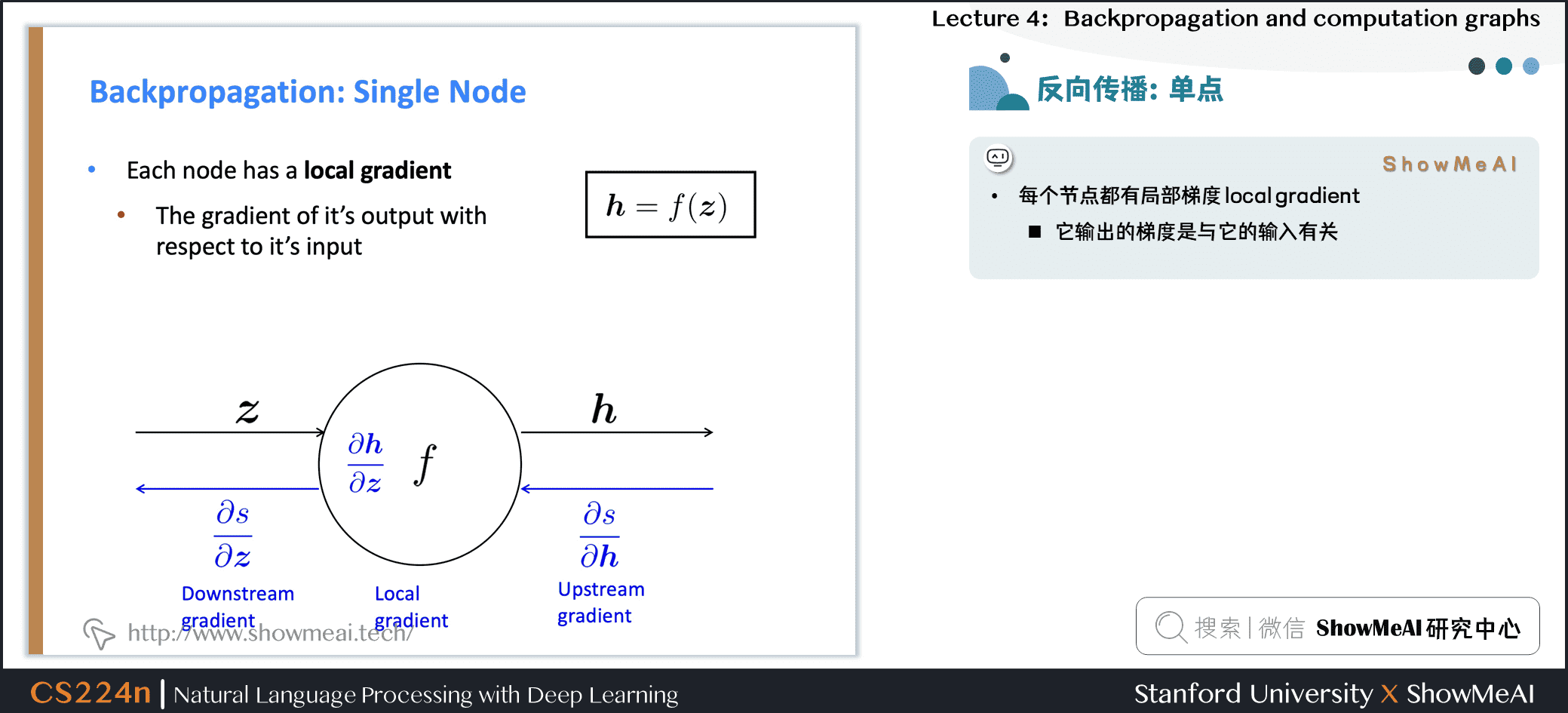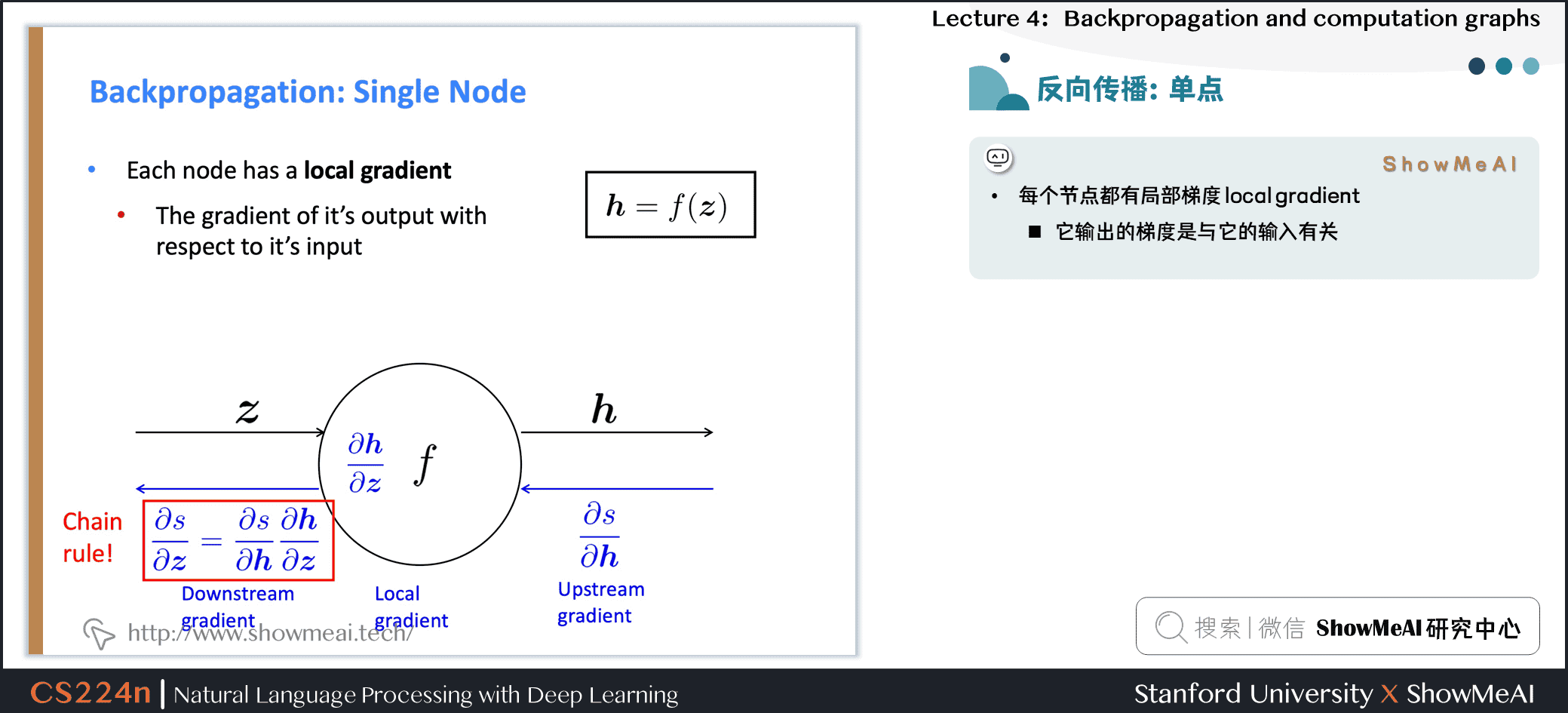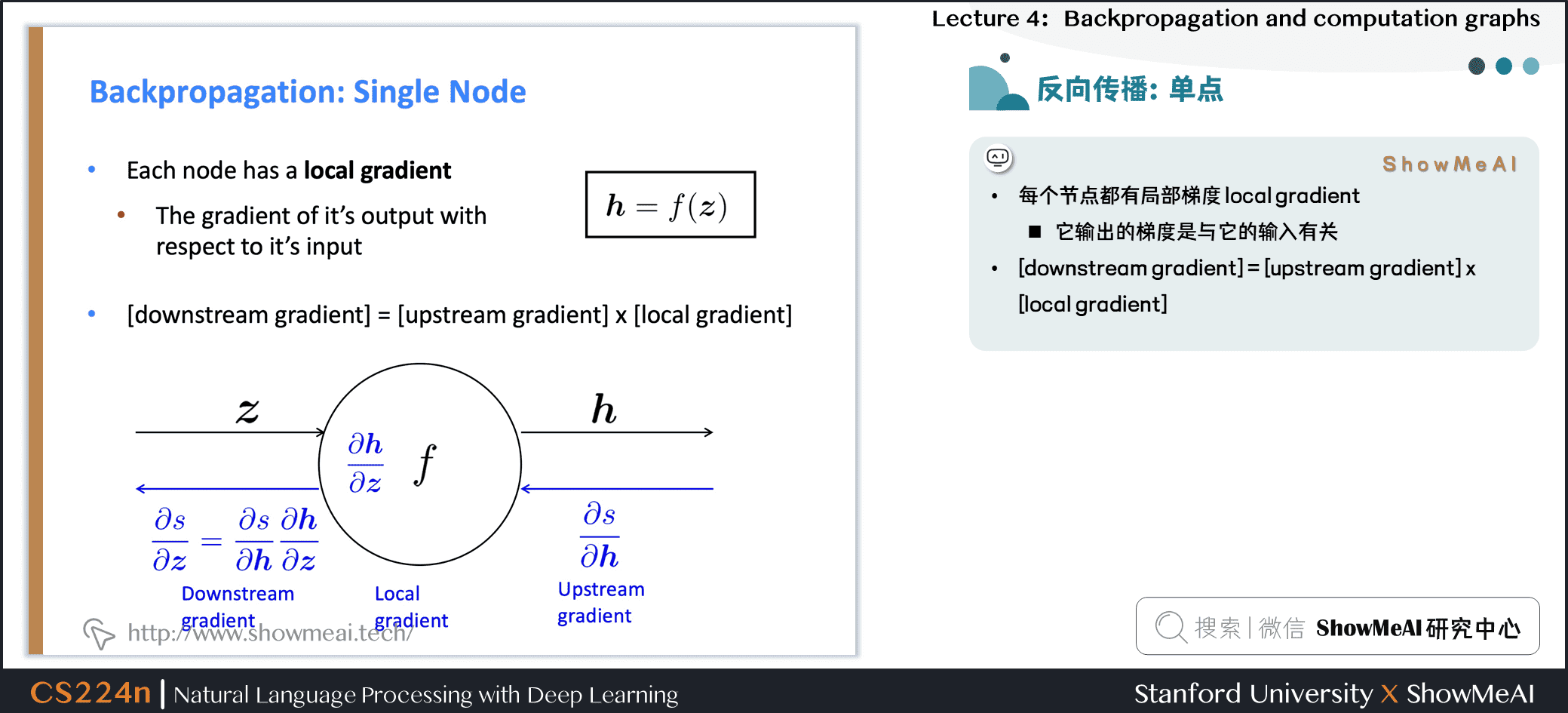
  • 每个节点都有局部梯度 local gradient

    • 它输出的梯度是与它的输入有关

  • 每个节点都有局部梯度 local gradient

    • n它输出的梯度是与它的输入有关

  • 每个节点都有局部梯度 local gradient

    • 它输出的梯度是与它的输入有关

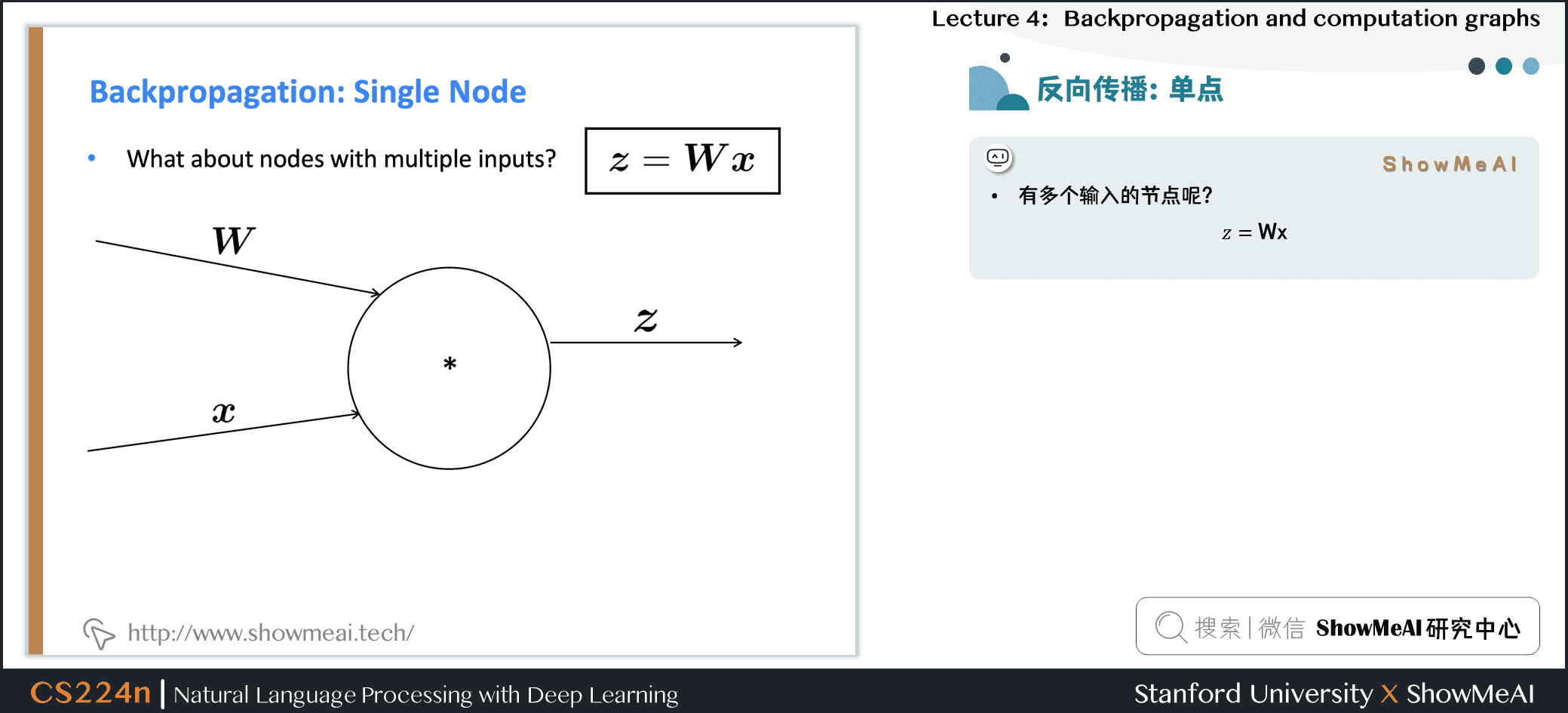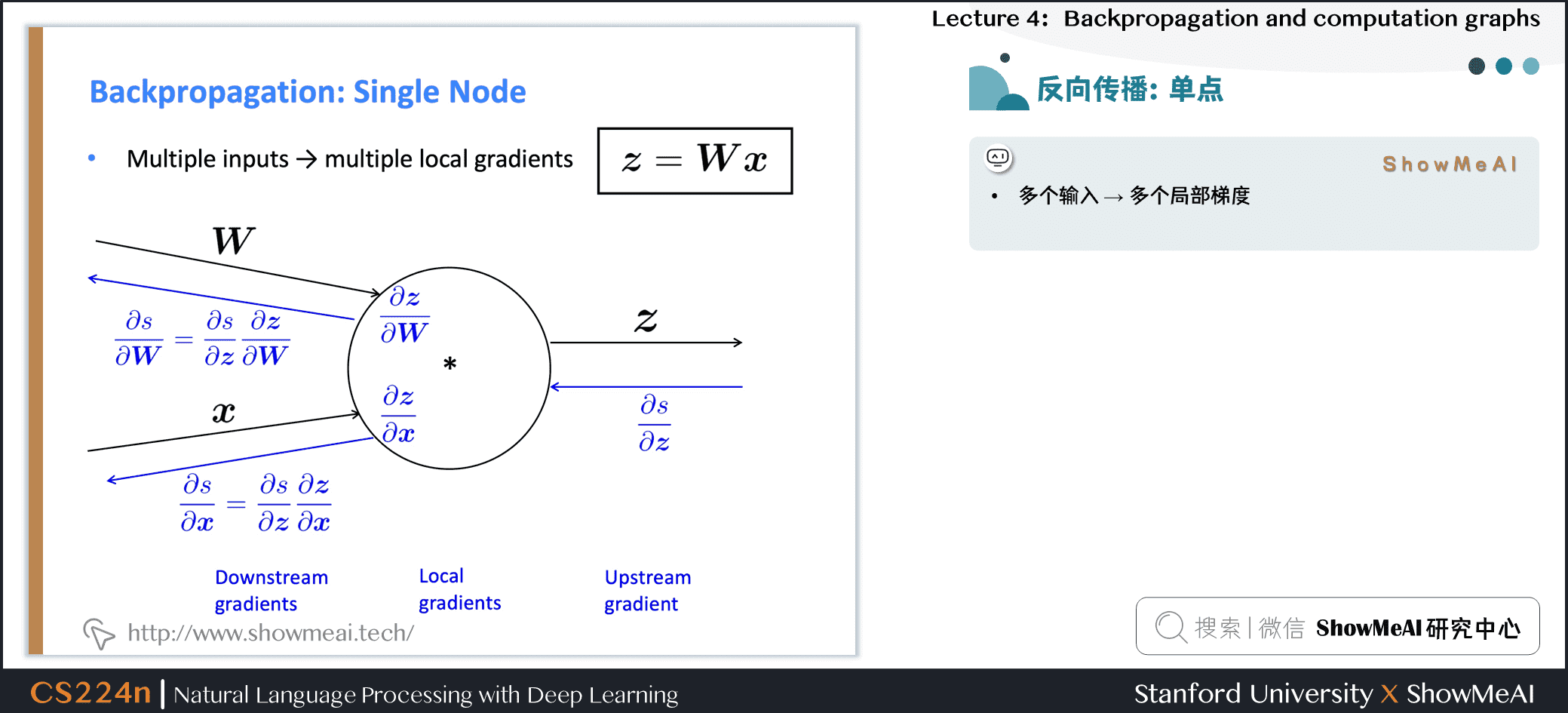
反向传播：单点

  • 有多个输入的节点呢？\(z=Wx\)
  • 多个输入 → 多个局部梯度

2.4 反向传播计算图示例

示例

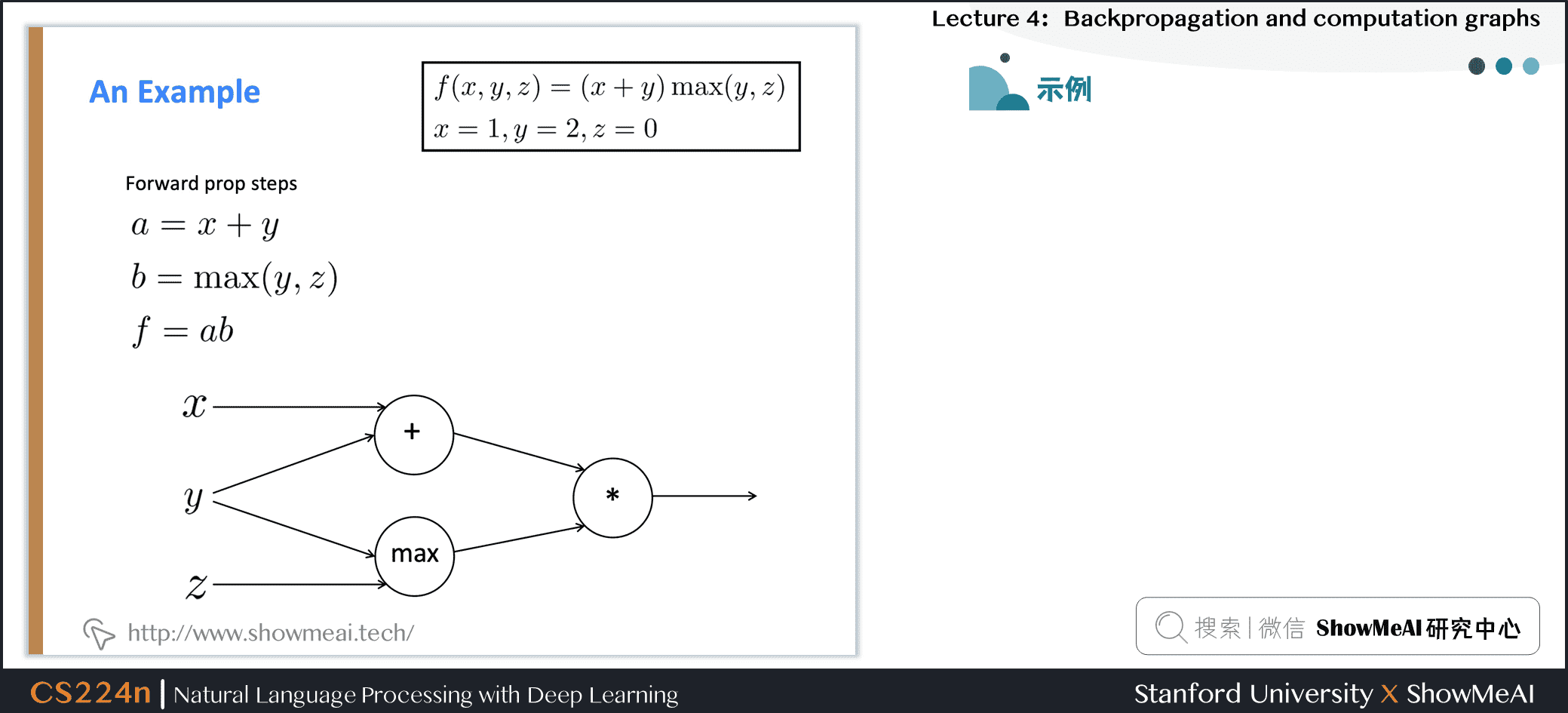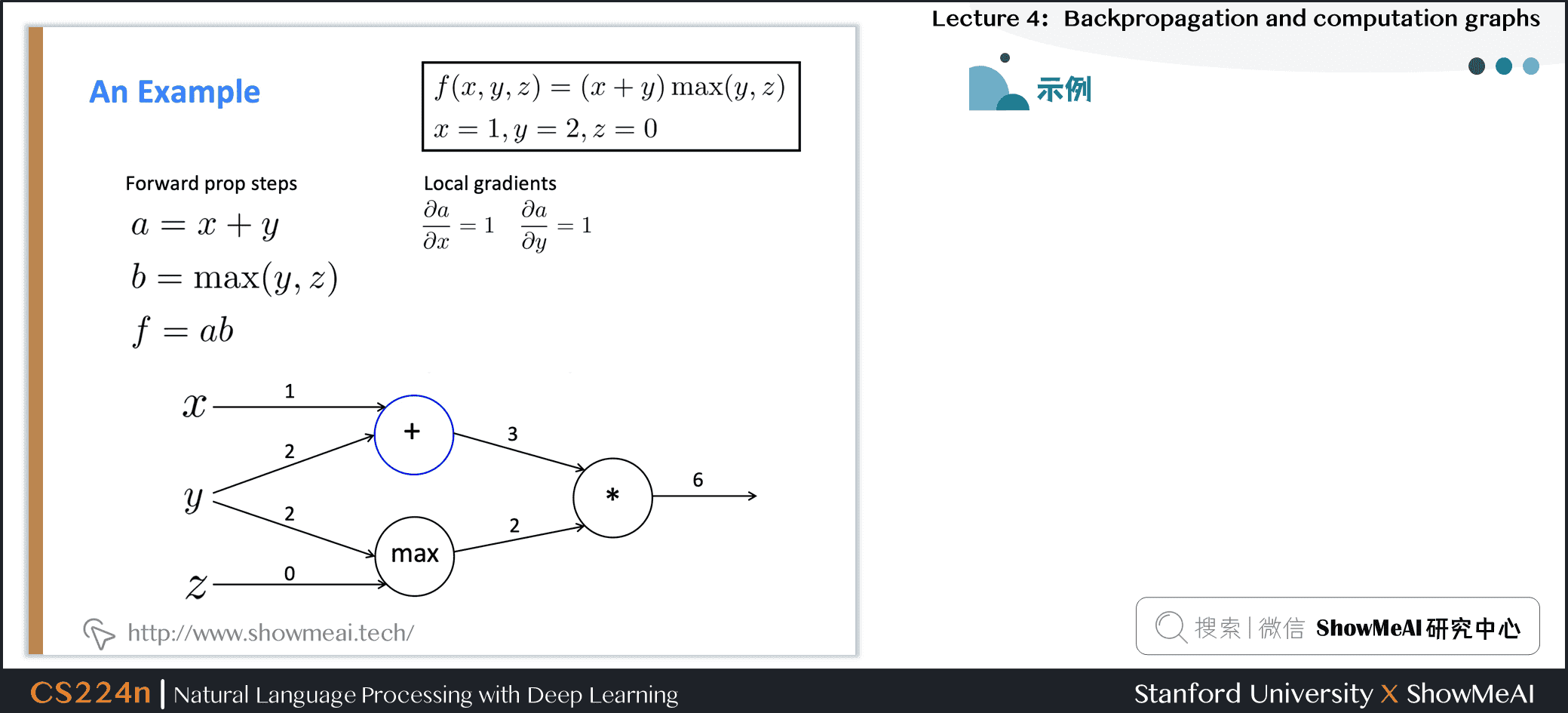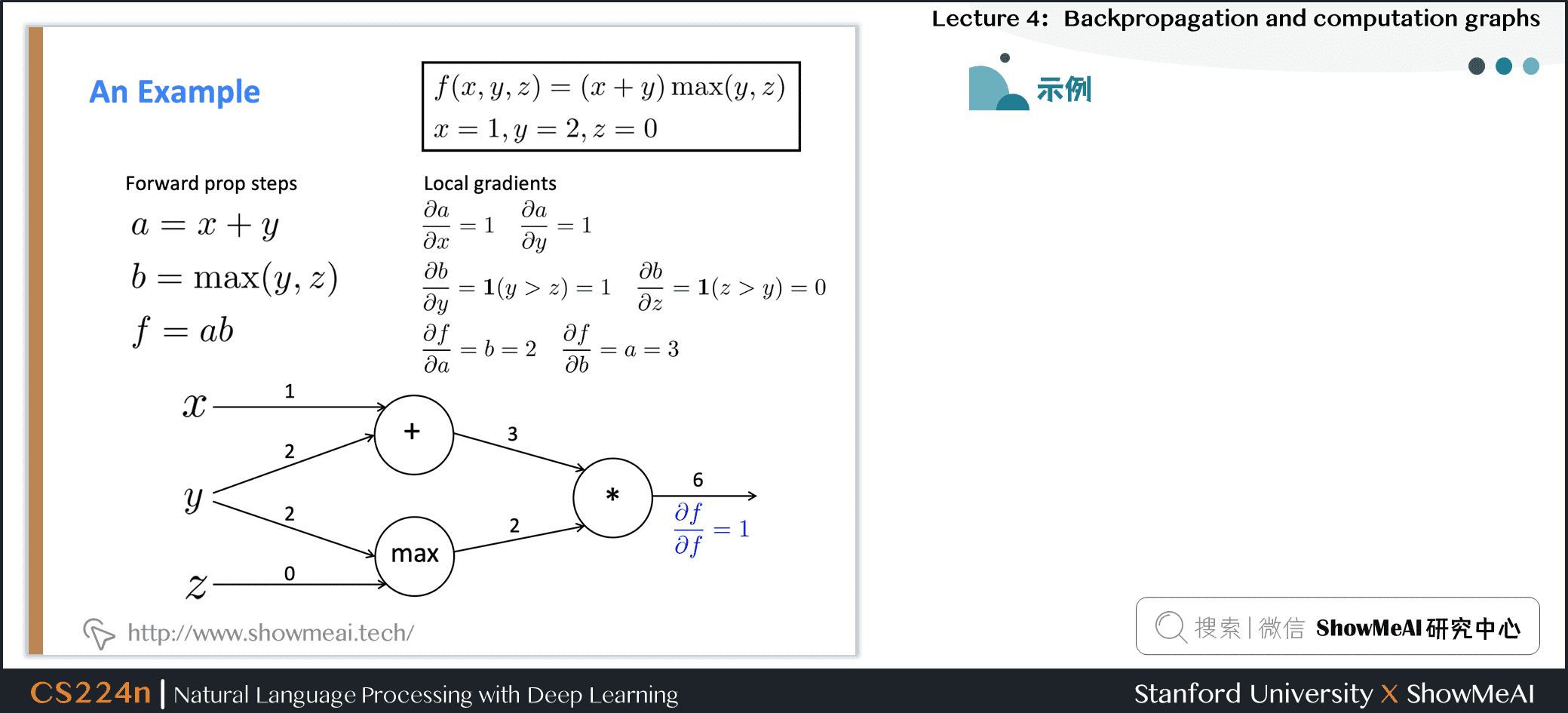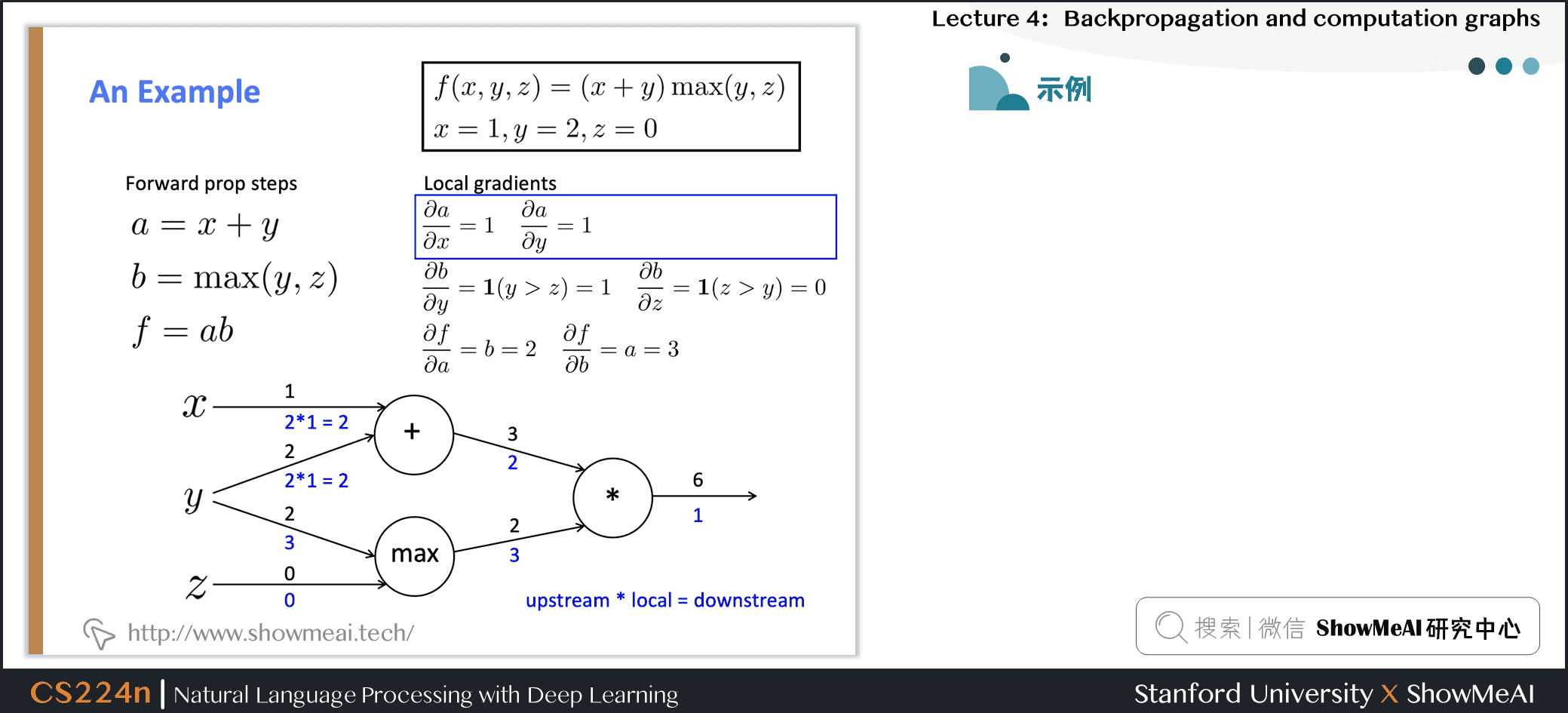
2.5 求和形态的梯度计算

上图中的 \(\frac{\partial f}{\partial y}\) 的梯度的计算

\[\begin{aligned} a &= x + y \\ b &= max(y,z)\\ f &= ab \end{aligned} \]

\[\frac{\partial f}{\partial y} = \frac{\partial f}{\partial a}\frac{\partial a}{\partial y} + \frac{\partial f}{\partial b}\frac{\partial b}{\partial y} \]

2.6 直挂理解神经元的梯度传递

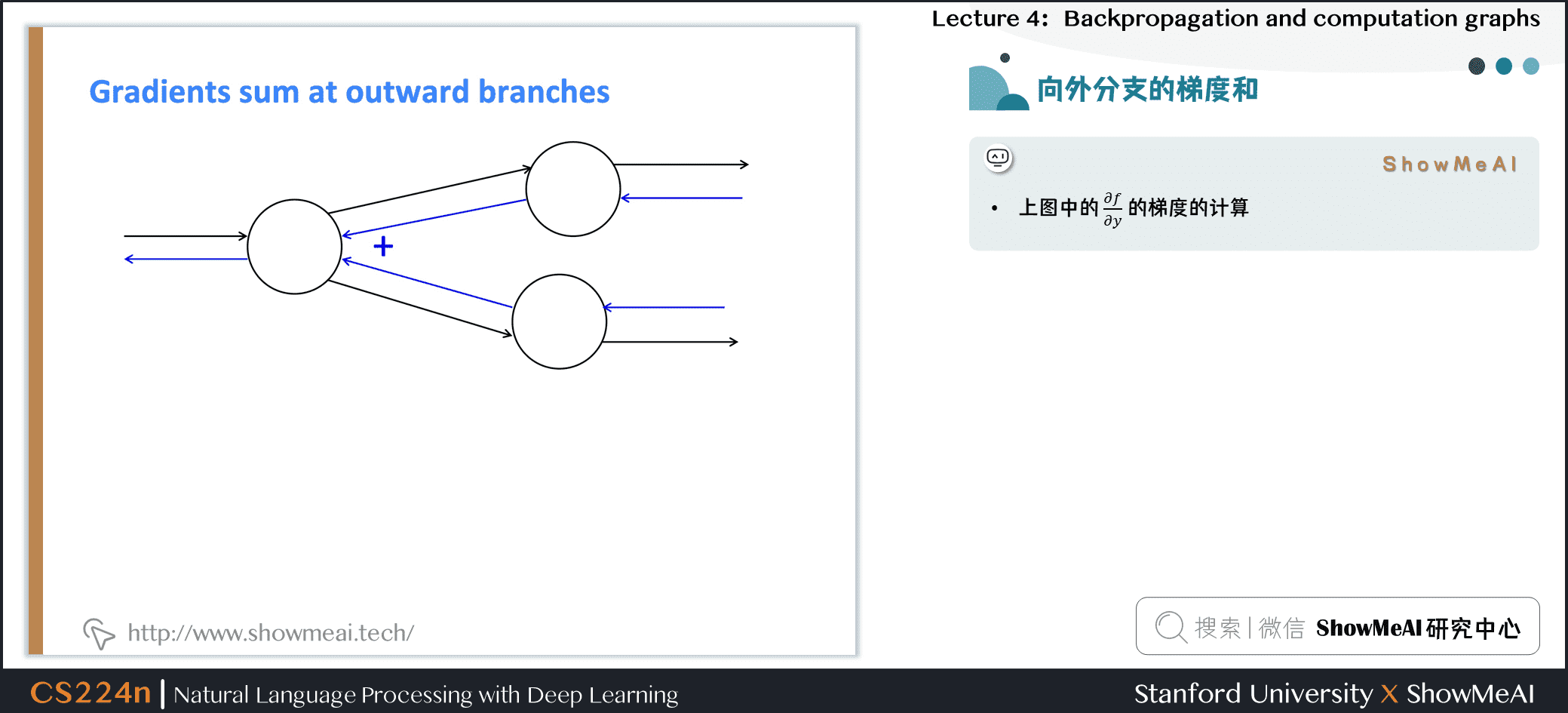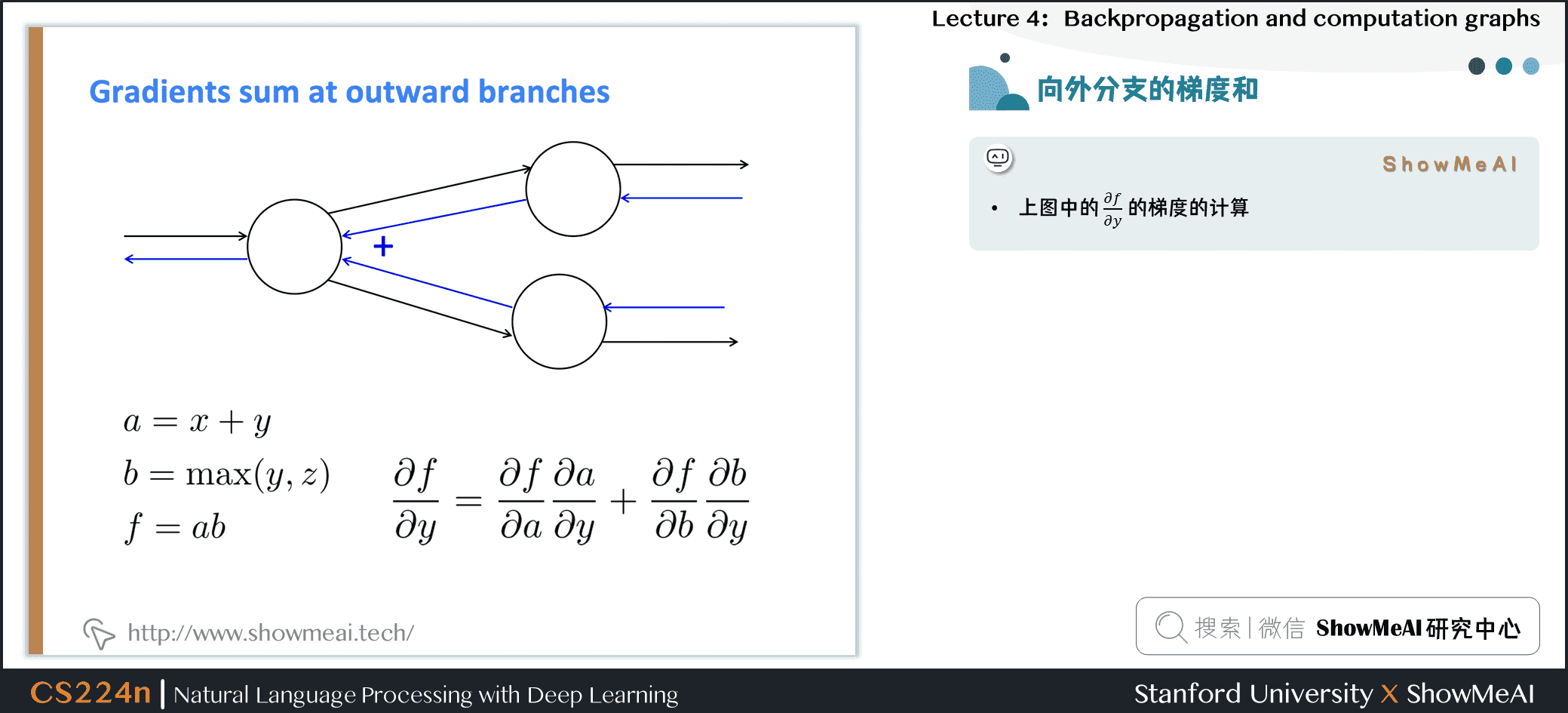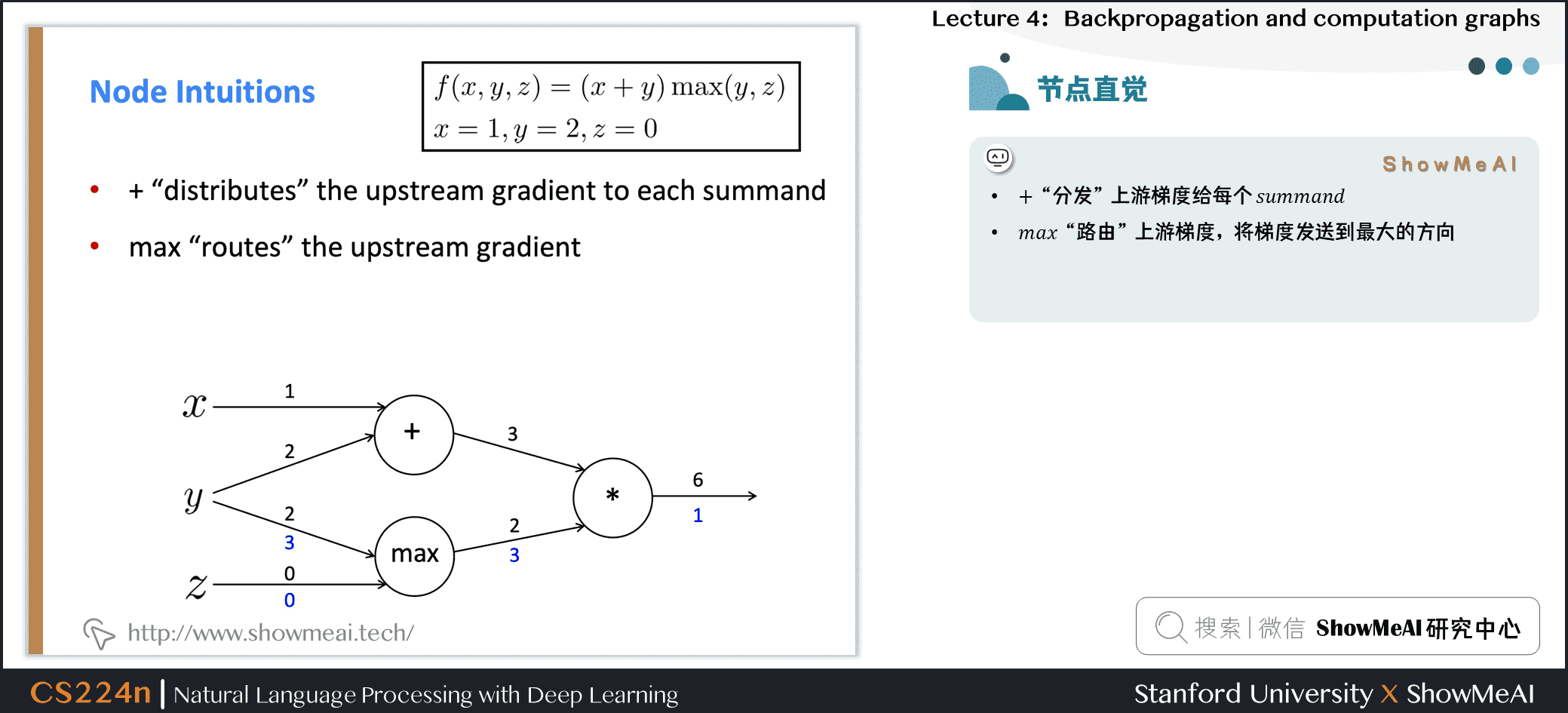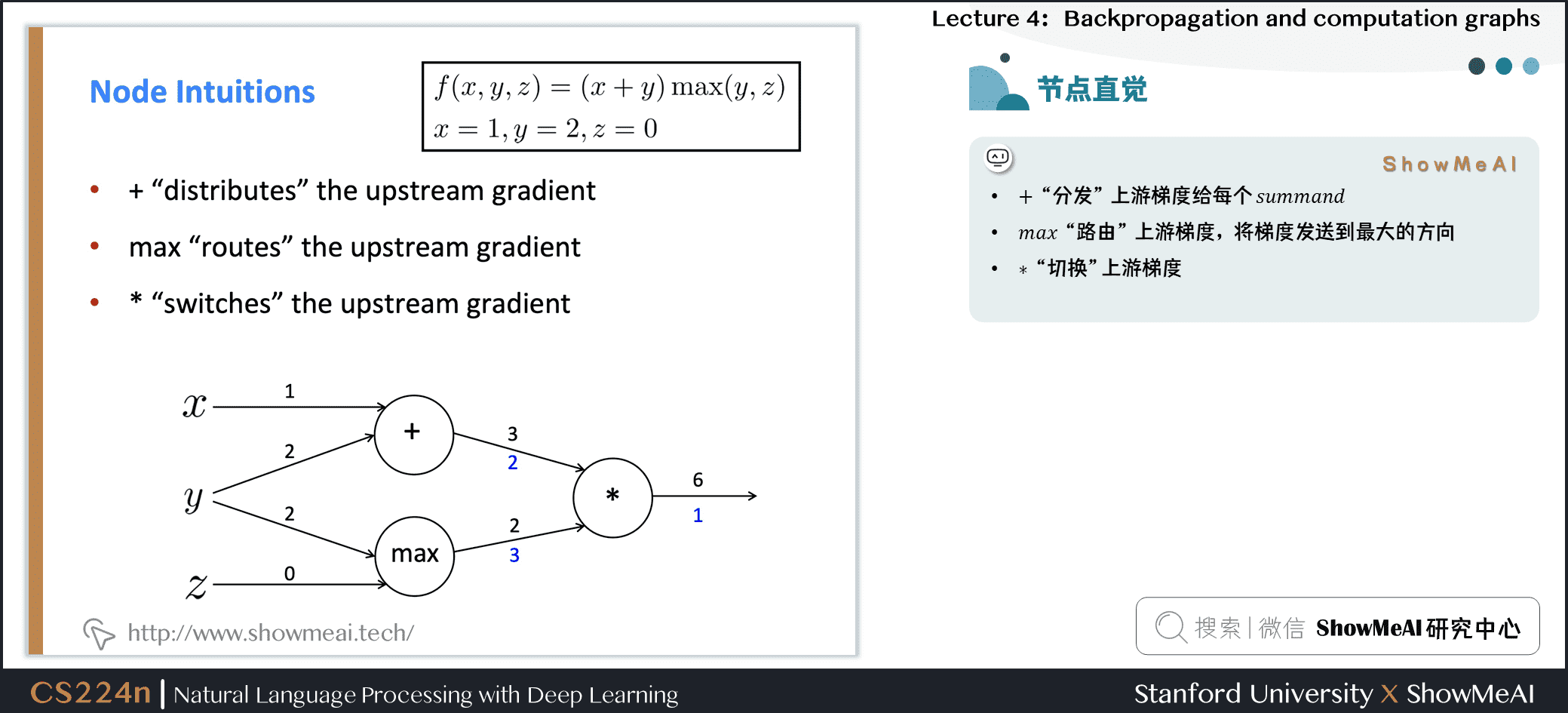
直观理解神经元的梯度传递

  • \(+\) “分发” 上游梯度
  • \(max\) “路由” 上游梯度，将梯度发送到最大的方向
  • \(\ast\) “切换”上游梯度

2.7 同步计算所有梯度以提速

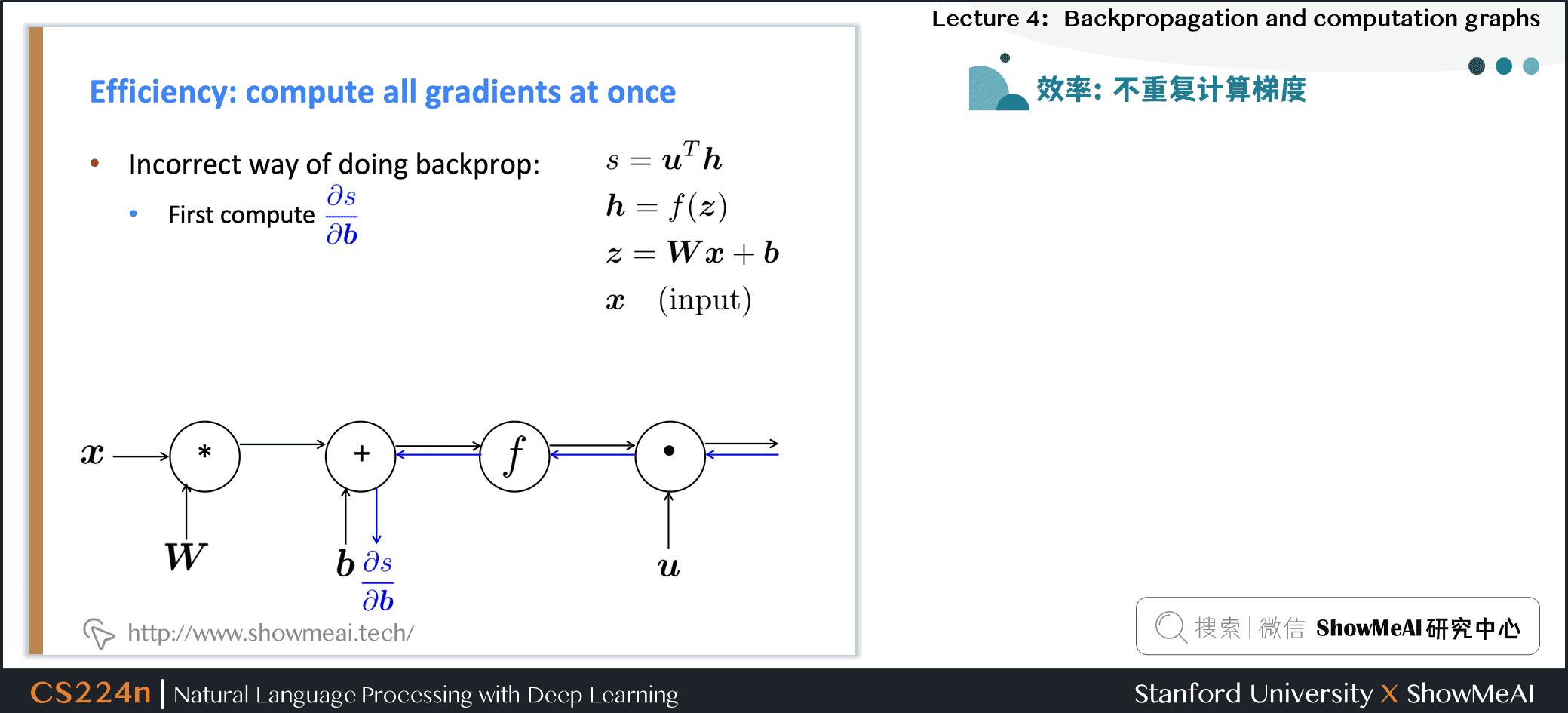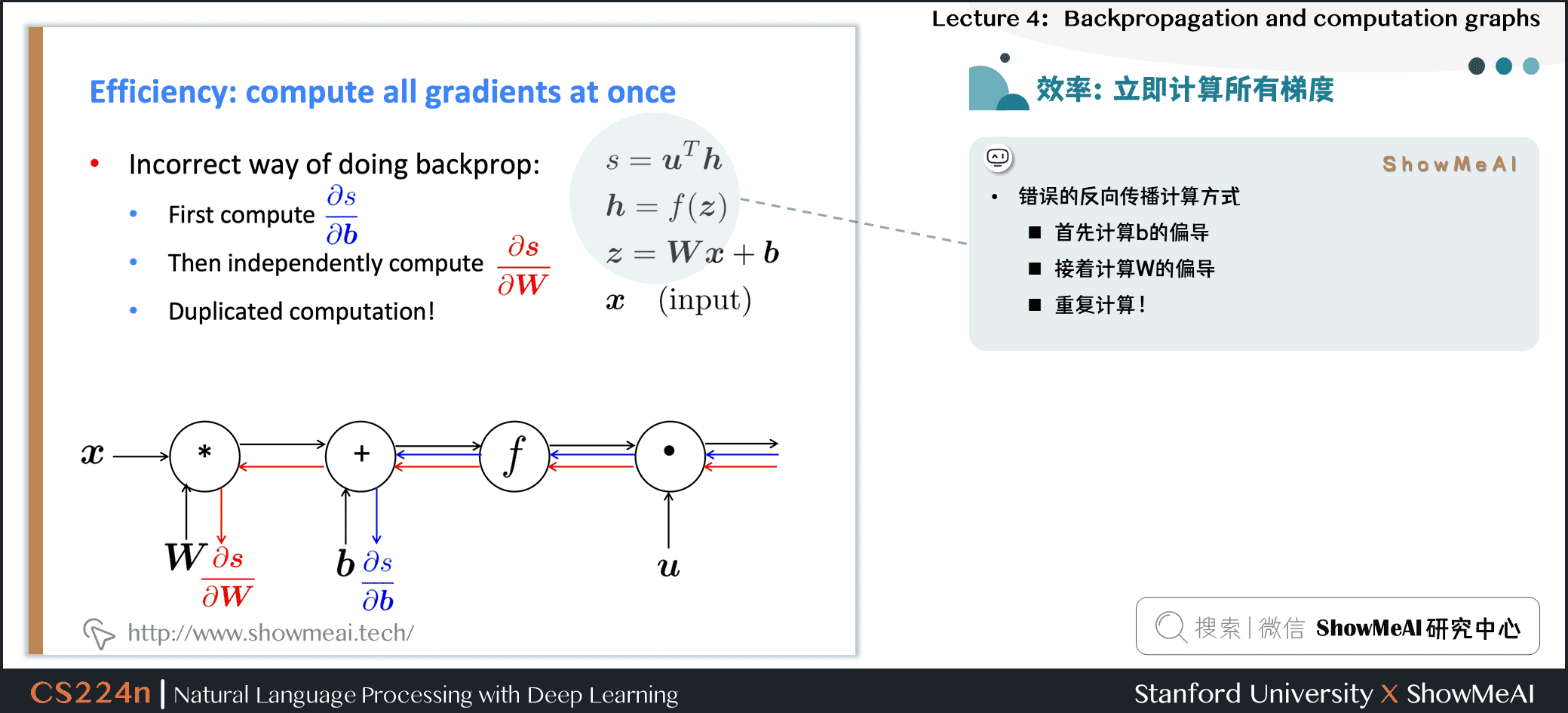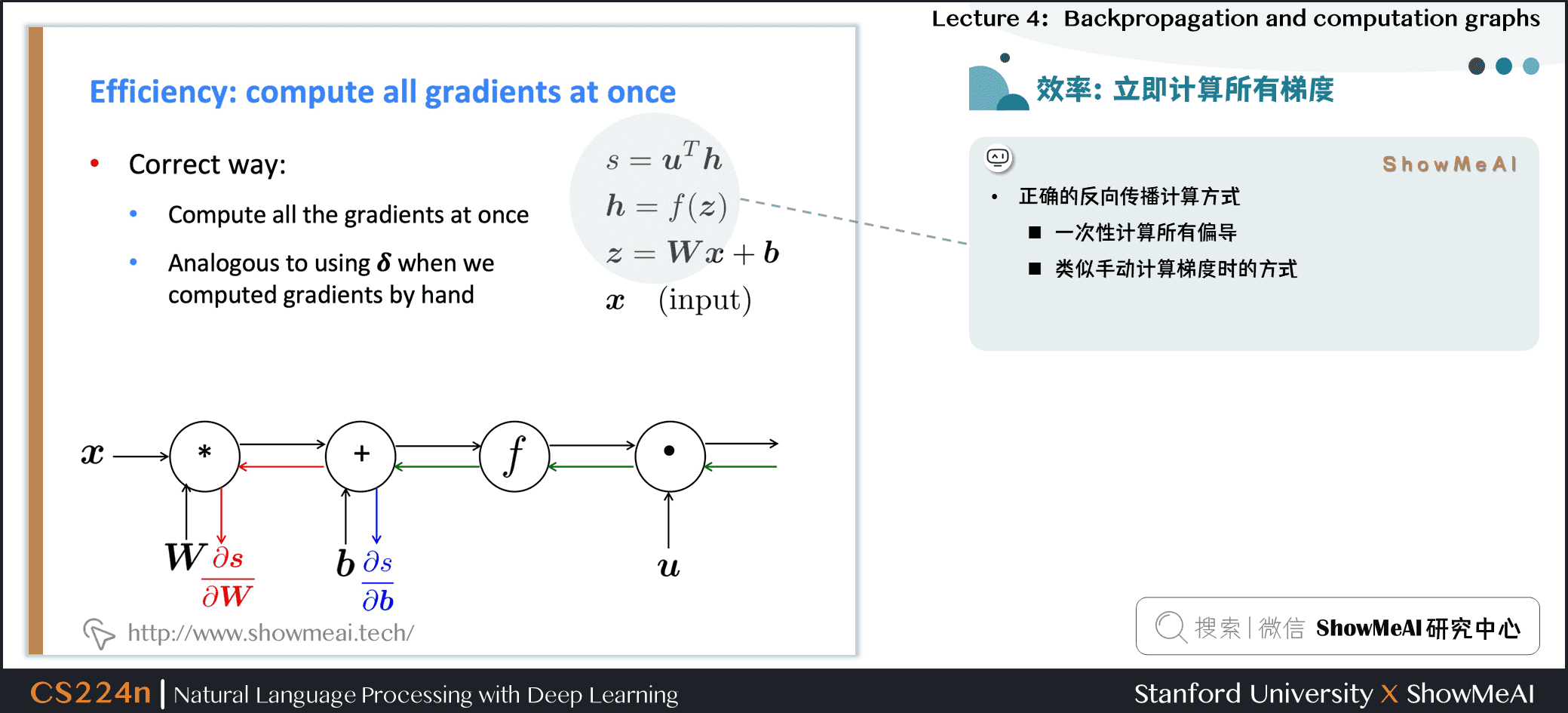
同步计算所有梯度以提速

  • 错误的反向传播计算方式

    • 先计算\(b\)的偏导
    • 接着计算\(W\)的偏导
    • 重复计算！

  • 正确的反向传播计算方式

    • 一次性计算所有偏导
    • 类似手动计算梯度时的方式

2.8 一般计算图中的反向传播

一般计算图中的反向传播

  • Fprop：按拓扑排序顺序访问节点

    • 计算给定父节点的节点的值

  • Bprop：

    • 初始化输出梯度为 1
    • 以相反的顺序方位节点，使用节点的后继的梯度来计算每个节点的梯度
    • \(\{y_1,y_2,\cdots,y_n\}\) 是 \(x\) 的后继

\[\frac{\partial z}{\partial x} = \sum_{i=1}^n \frac{\partial z}{\partial y_i}\frac{\partial y_i}{\partial x} \]

  • 正确地说，Fprop 和 Bprop 的计算复杂度是一样的
  • 一般来说，我们的网络有固定的层结构，所以我们可以使用矩阵和雅可比矩阵

2.9 自动微分

自动微分

  • 梯度计算可以从 Fprop 的符号表达式中自动推断
  • 每个节点类型需要知道如何计算其输出，以及如何在给定其输出的梯度后计算其输入的梯度
  • 现代DL框架(Tensorflow, Pytoch)为您做反向传播，但主要是令作者手工计算层/节点的局部导数

2.10 反向传播的实现

反向传播的实现

为了计算反向传播，我们需要在前向传播时存储一些变量的值

2.11 实现：前向/反向API

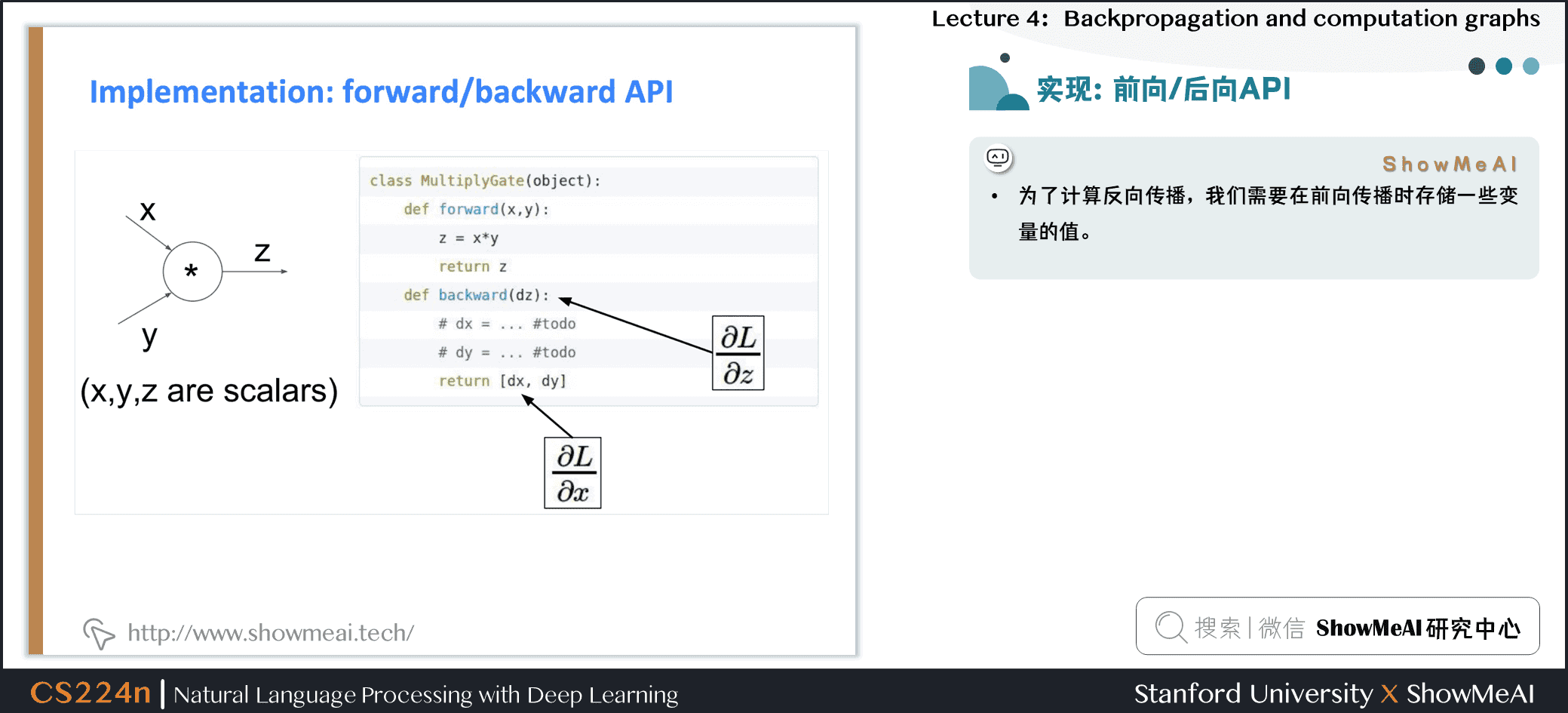
实现：前向/反向API

为了计算反向传播，我们需要在前向传播时存储一些变量的值

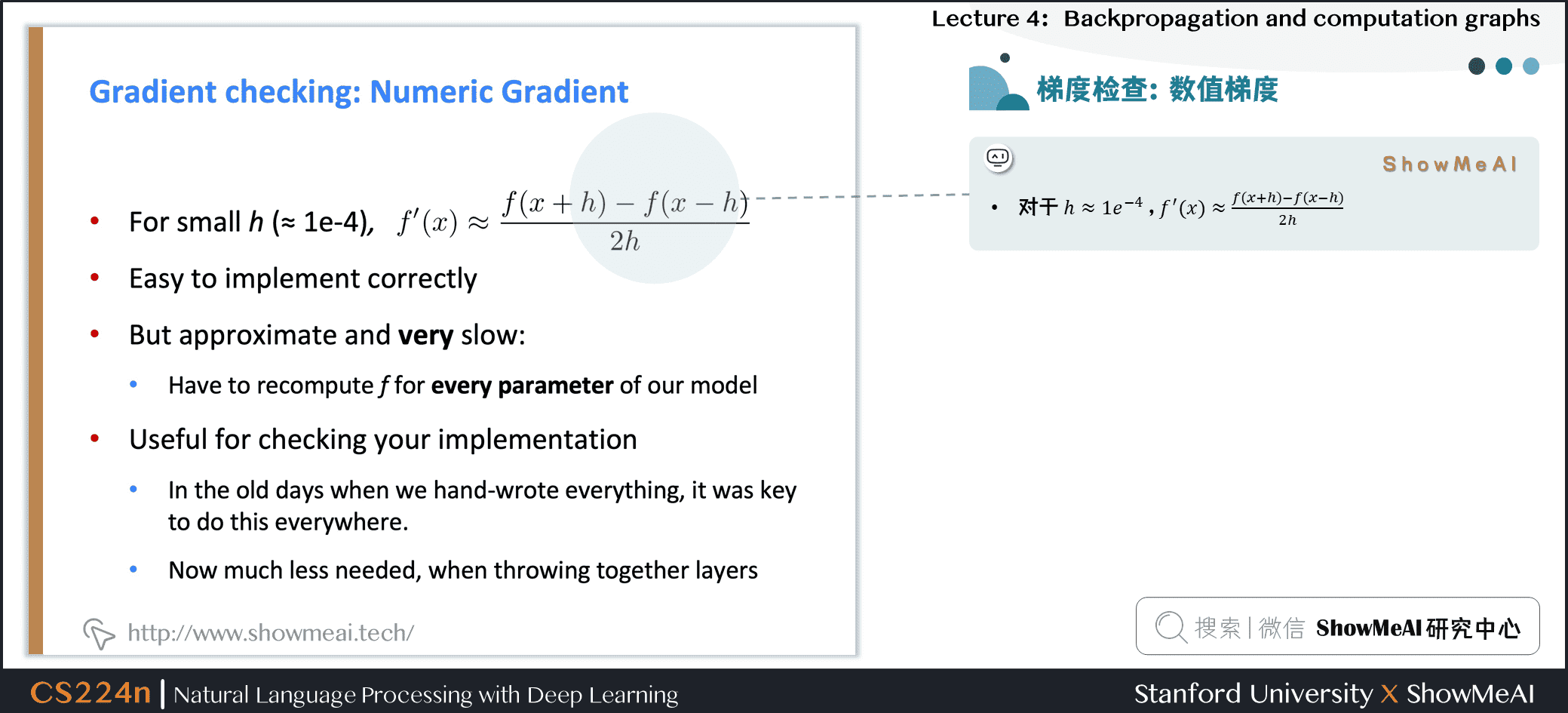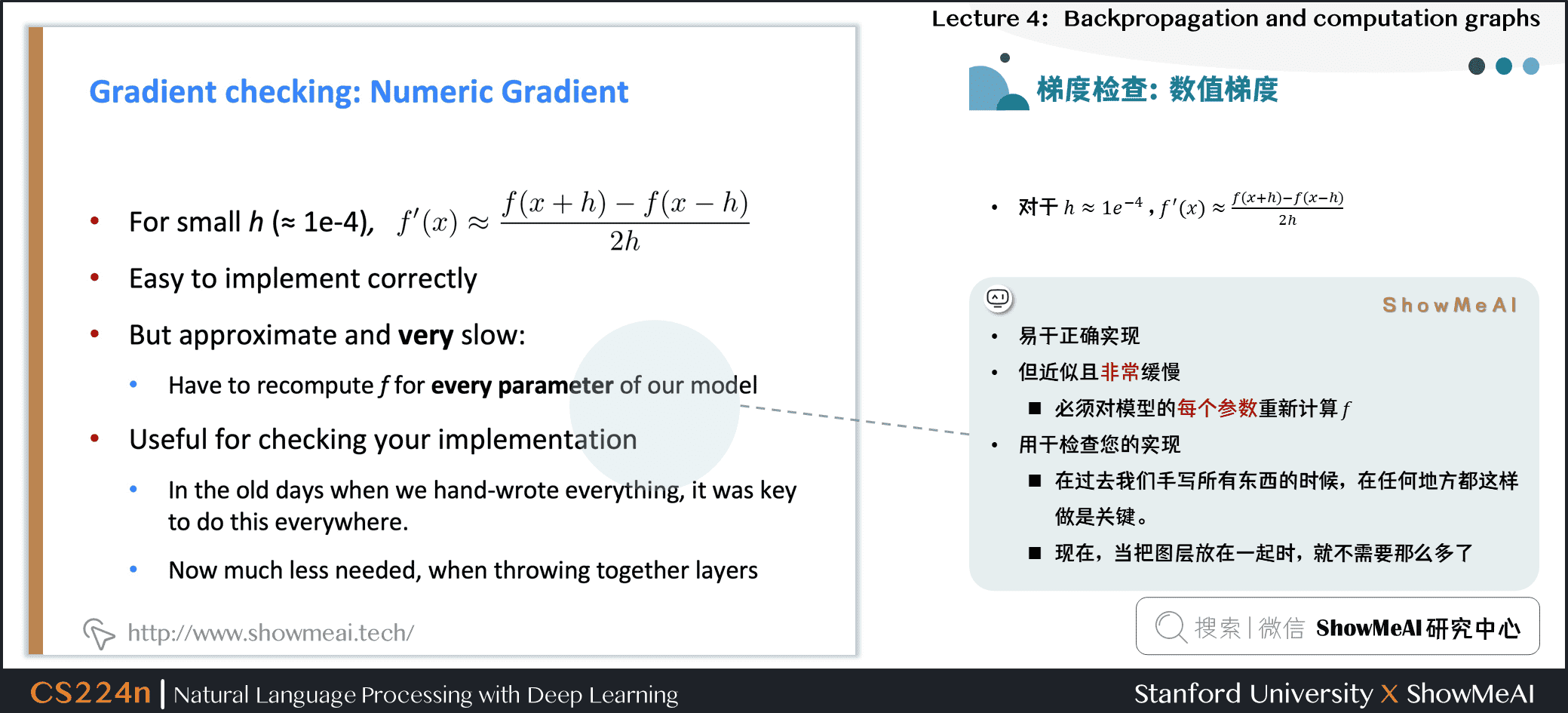
2.12 梯度检查：数值梯度

梯度检查：数值梯度

  • 对于 \(h \approx 1e^{-4}\) , \(f^{\prime}(x) \approx \frac{f(x+h)-f(x-h)}{2 h}\)

  • 易于正确实现

  • 但近似且非常缓慢

    • 必须对模型的每个参数重新计算 \(f\)

  • 用于检查您的实现

    • 在过去我们手写所有东西的时候，在任何地方都这样做是关键。
    • 现在，当把图层放在一起时，就不需要那么多了

2.13 总结

总结

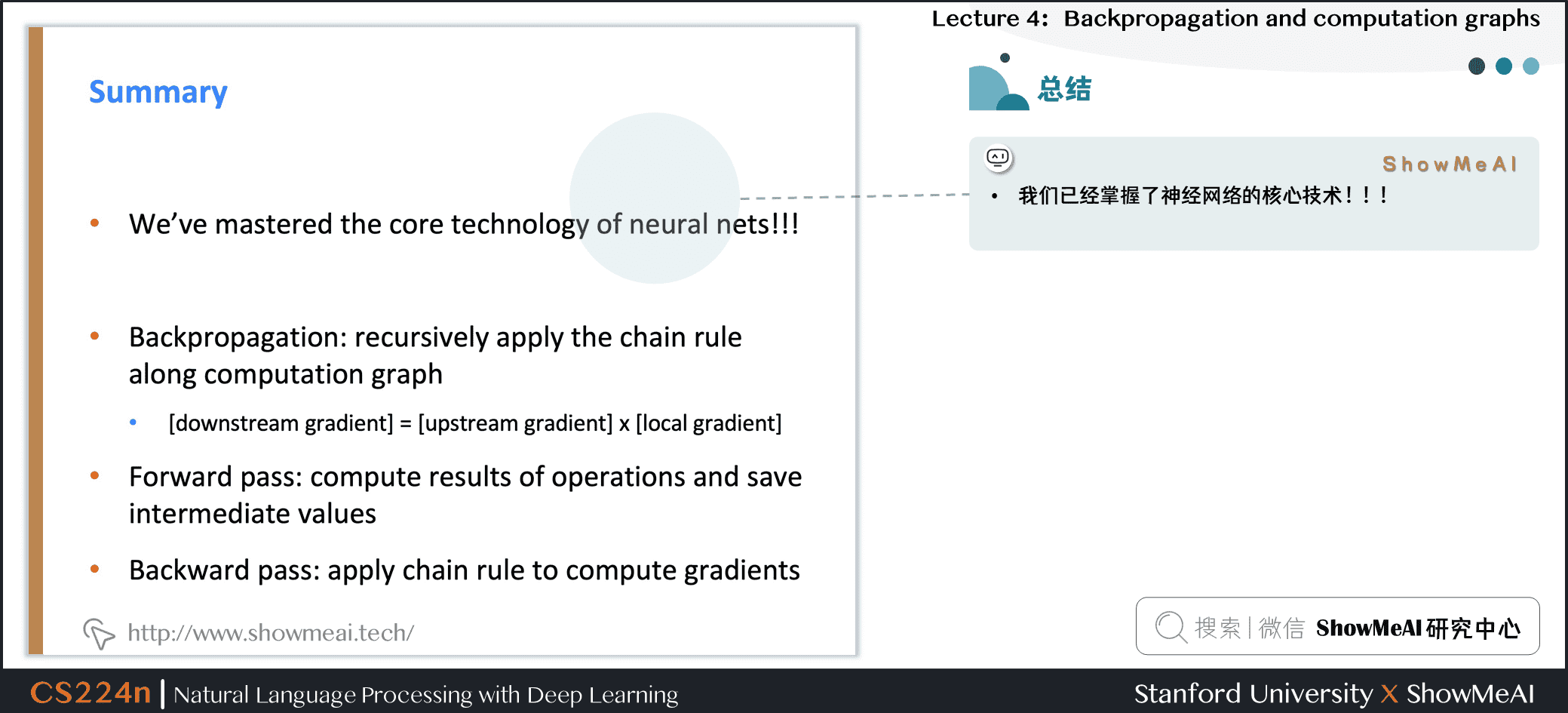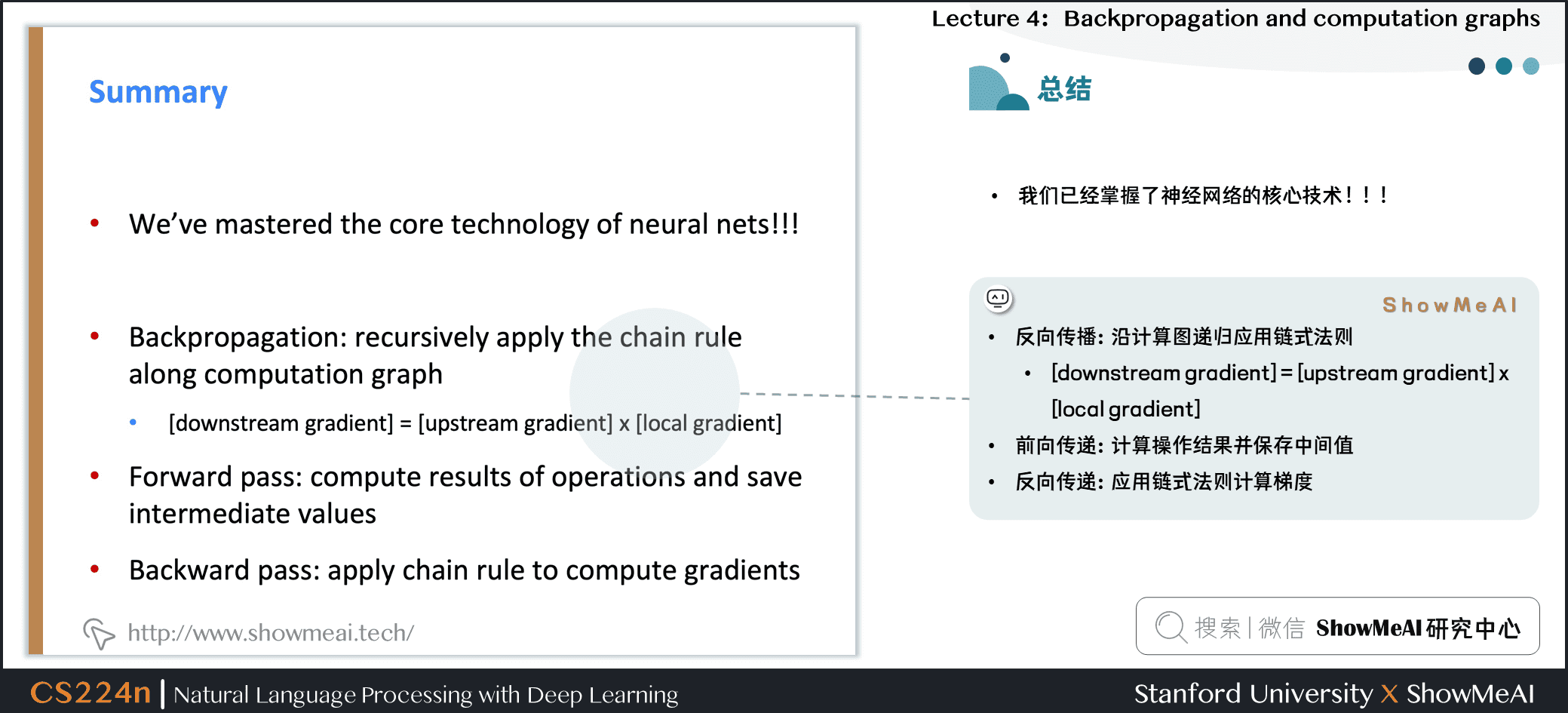
  • 我们已经掌握了神经网络的核心技术
  • 反向传播：沿计算图递归应用链式法则
    • [downstream gradient] = [upstream gradient] x [local gradient]
  • 前向传递：计算操作结果并保存中间值
  • 反向传递：应用链式法则计算梯度

2.14 为什么要学习梯度的所有细节？

为什么要学习梯度的所有细节？

  • 现代深度学习框架为您计算梯度

  • 但是，当编译器或系统为您实现时，为什么要学习它们呢？

    • 了解底层原理是有帮助的

  • 反向传播并不总是完美地工作

    • 理解为什么对调试和改进模型至关重要
    • 参见 Karpathy文章

  • 未来课程的例子:爆炸和消失的梯度

3.神经网络训练实用知识技能

3.1 模型正则化防止过拟合

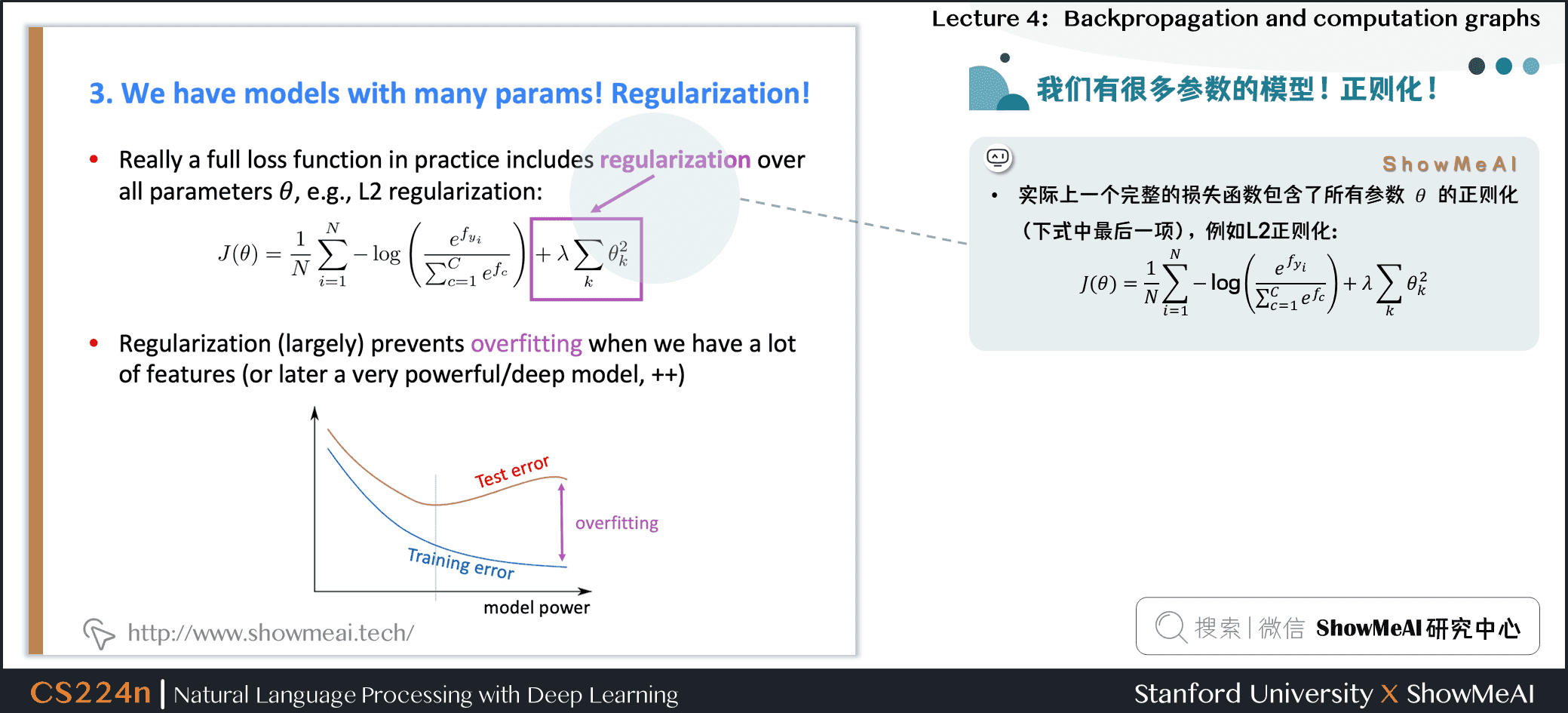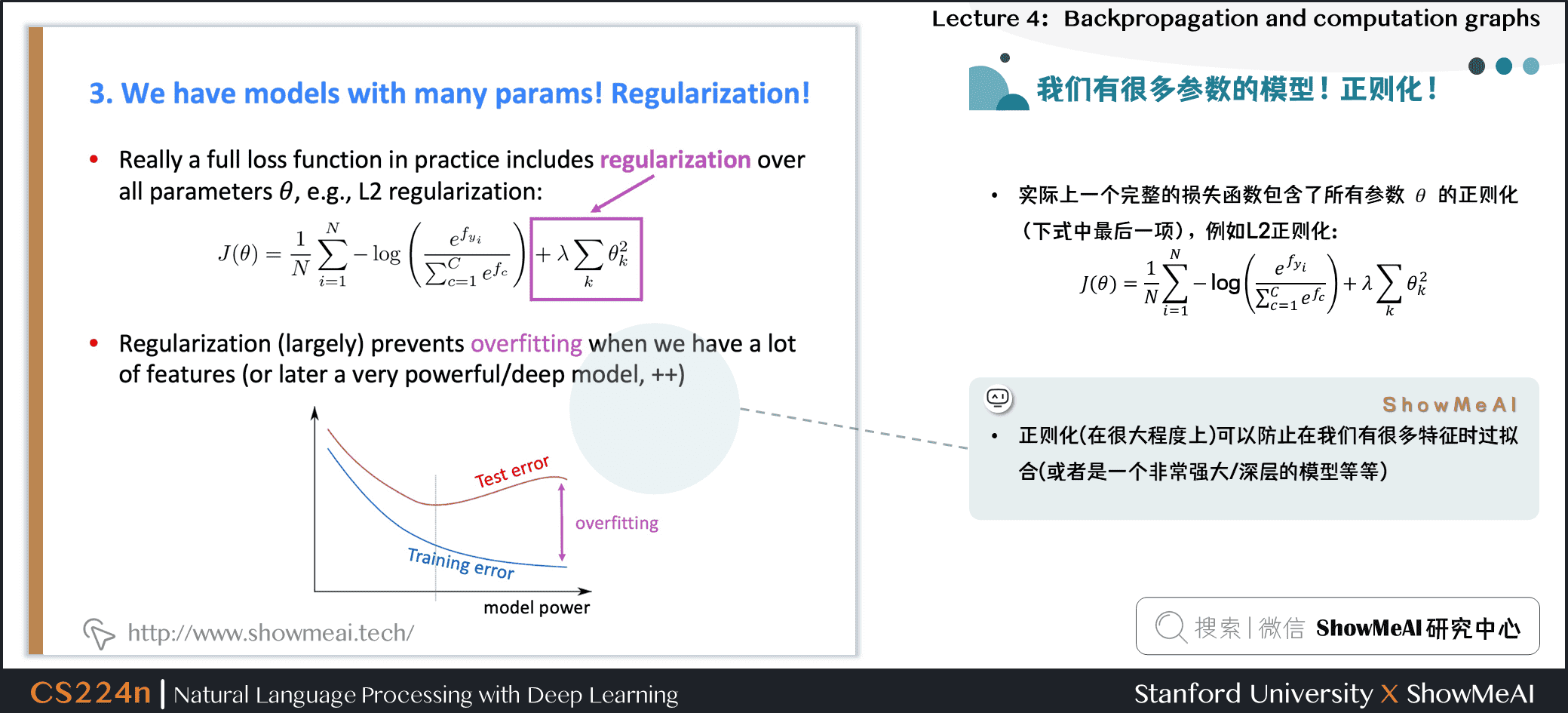
模型正则化防止过拟合

  • 实际上一个完整的损失函数包含了所有参数\(\theta\)的正则化（下式中最后一项），例如L2正则化：

\[J(\theta)=\frac{1}{N} \sum_{i=1}^{N}-\log (\frac{e^{f_{y_{i}}}}{\sum_{c=1}^{C} e^{f_{c}}})+\lambda \sum_{k} \theta_{k}^{2} \]

  • 正则化(在很大程度上)可以防止在我们有很多特征时过拟合(或者是一个非常强大/深层的模型等等)

3.2 向量化形态

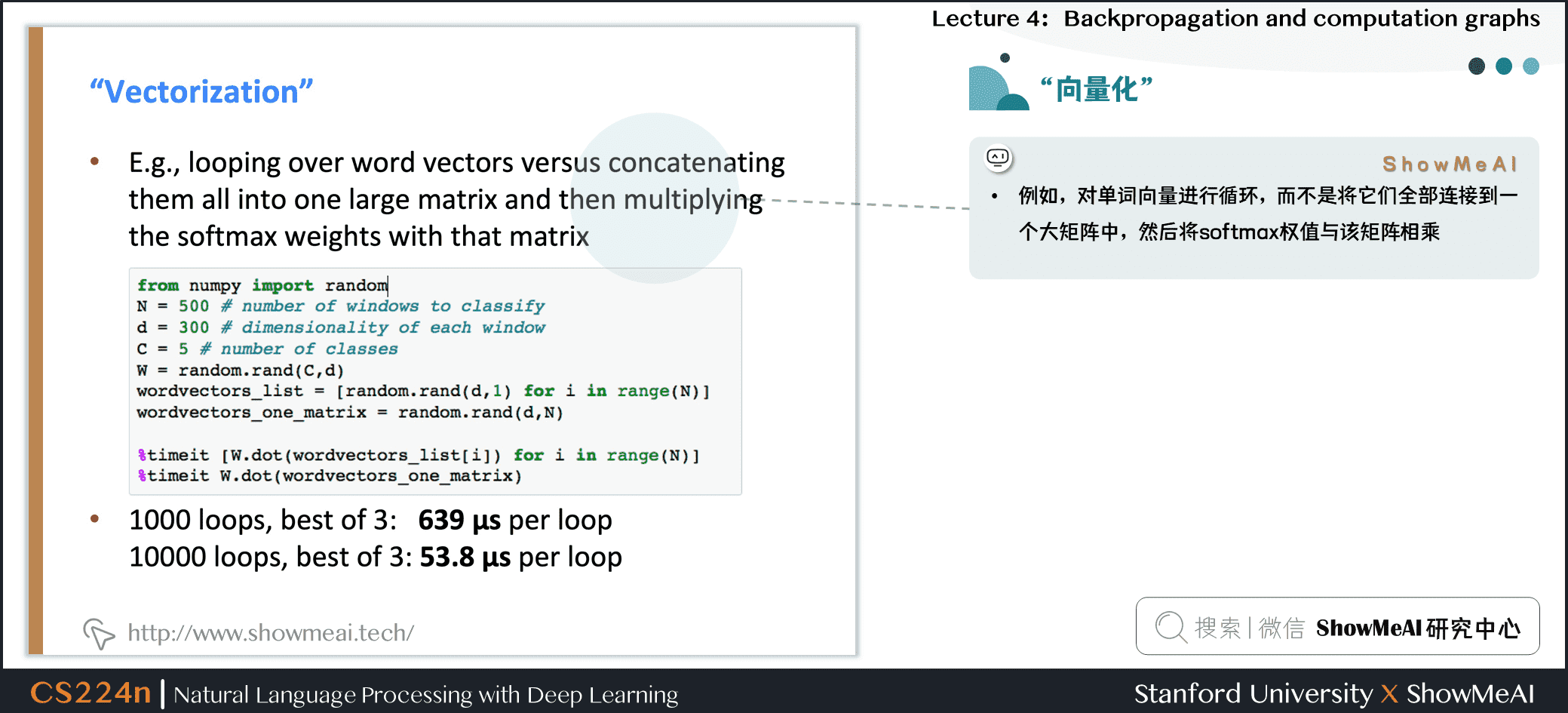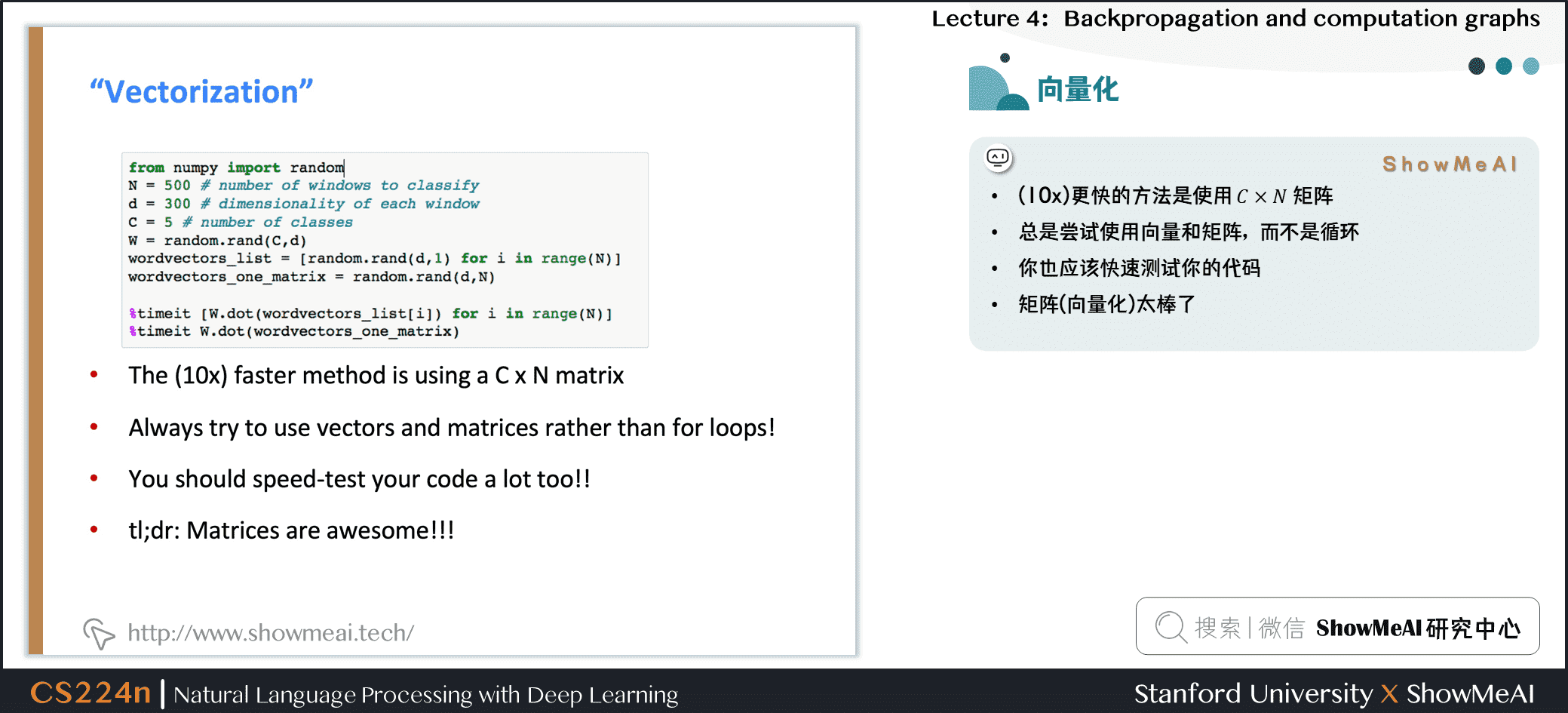
向量化形态

  • 例如，对单词向量进行循环，而不是将它们全部连接到一个大矩阵中，然后将softmax权值与该矩阵相乘

    • 1000 loops, best of 3: 639 μs per loop
    • 10000 loops, best of 3: 53.8 μs per loop

  • (10x)更快的方法是使用 \(C \times N\) 矩阵

  • 总是尝试使用向量和矩阵，而不是循环

  • 你也应该快速测试你的代码

  • 简单来说：矩阵向量化的方式太棒了

3.3 非线性：常规激活函数

非线性：常规激活函数

tanh 只是一个重新放缩和移动的 sigmoid (两倍陡峭，[-1,1])

\[\tanh (z)=2 logistic(2 z)-1 \]

logistic 和 tanh 仍然被用于特定的用途，但不再是构建深度网络的默认值。

tip：logistic和tanh

设计复杂的数学运算，指数计算会减慢速度。所以人们提出了 hard tanh，并且效果很不错。于是才有了 ReLU

3.4 非线性：新的激活函数

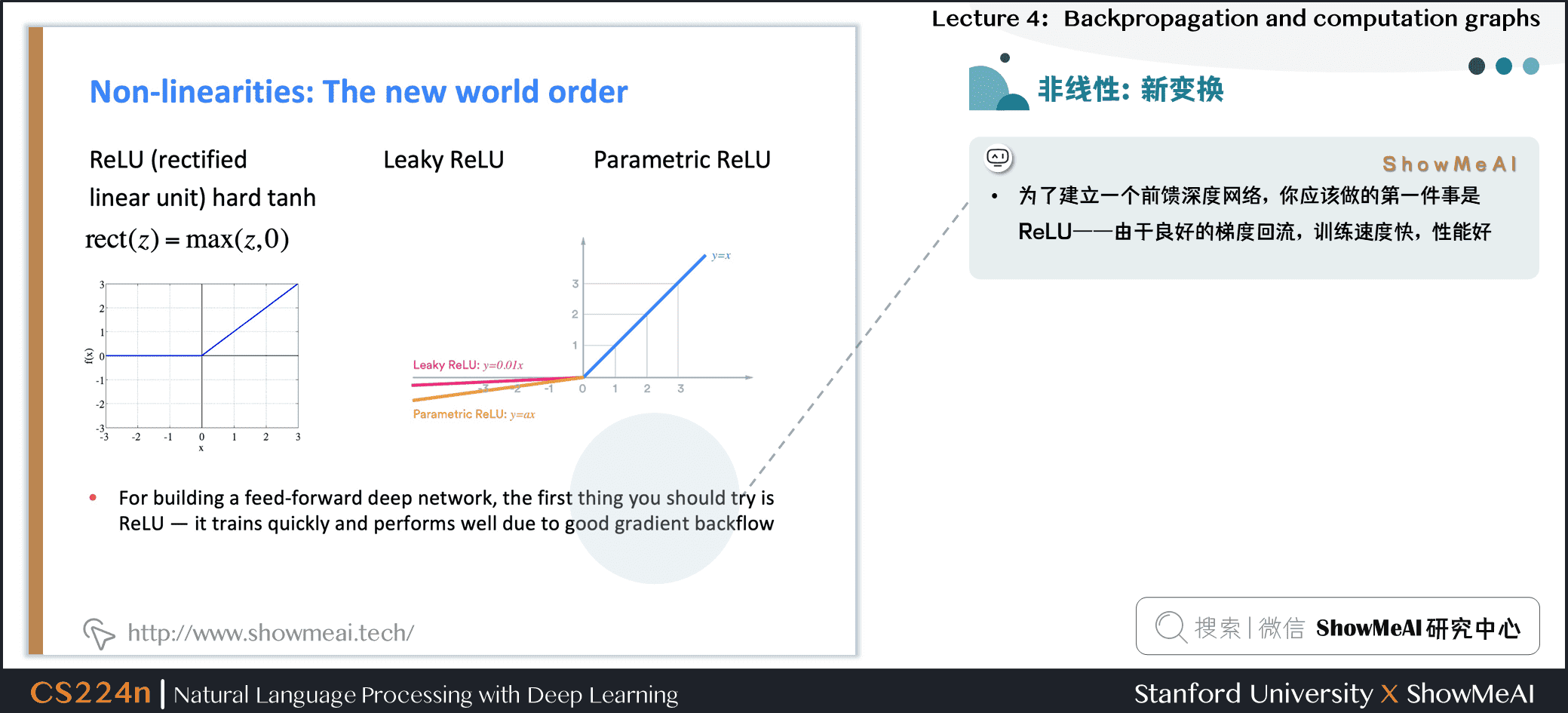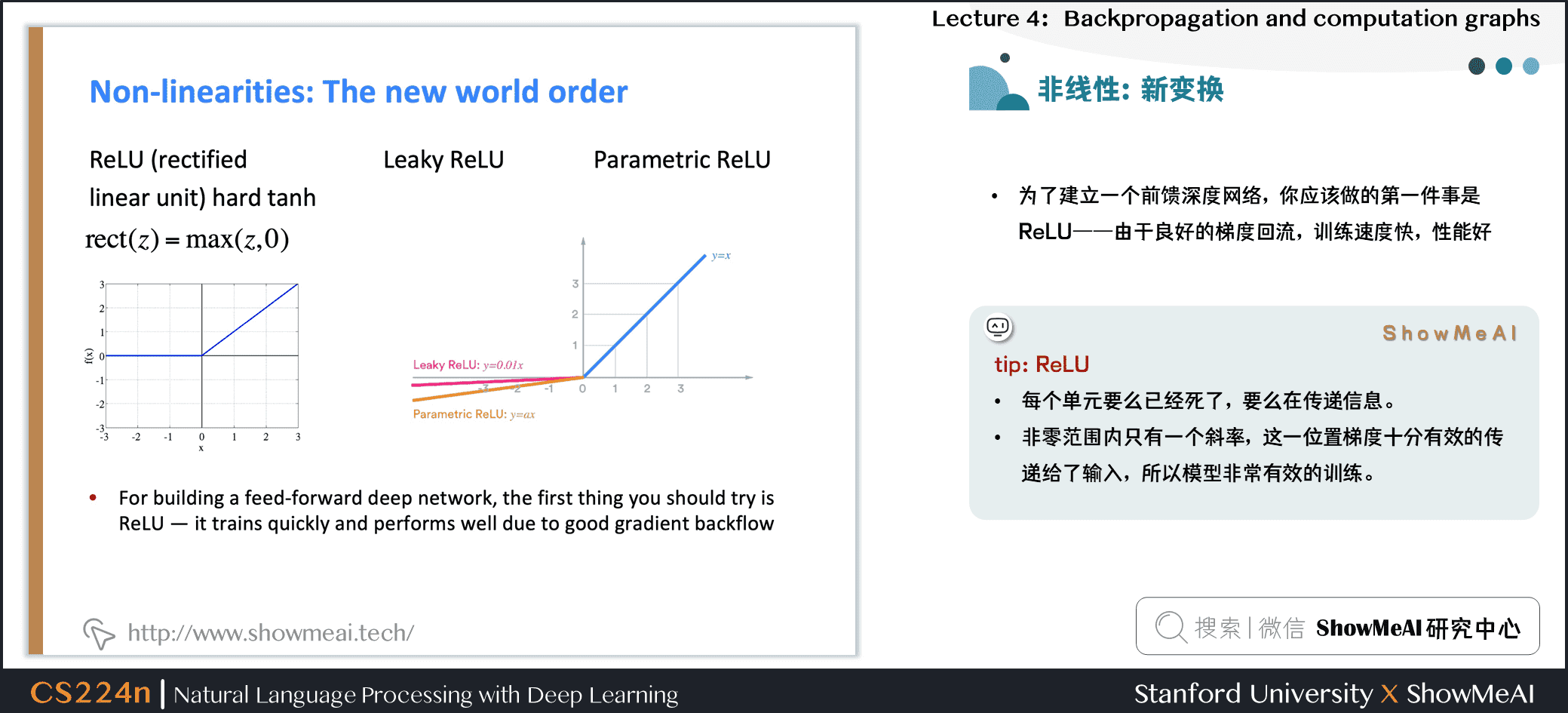
非线性：新的激活函数

  • 为了建立一个前馈深度网络，你应该做的第一件事是ReLU——由于良好的梯度回流，训练速度快，性能好

tip：ReLU

  • 每个单元要么已经死了，要么在传递信息。
  • 非零范围内只有一个斜率，这一位置梯度十分有效的传递给了输入，所以模型非常有效的训练

3.5 参数初始化

参数初始化

  • 通常 必须将权重初始化为小的随机值 （这样才能在激活函数的有效范围内， 即存在梯度可以使其更新）
    • 避免对称性妨碍学习/特殊化的
  • 初始化隐含层偏差为0，如果权重为0，则输出(或重构)偏差为最优值(例如，均值目标或均值目标的反s形)
  • 初始化 所有其他权重为 Uniform(–r, r)，选择使数字既不会太大也不会太小的 \(r\)
  • Xavier初始化中，方差与 fan-in \(n_{in}\) (前一层尺寸)和 fan-out \(n_{out}\)(下一层尺寸)成反比

\[Var(W_i)=\frac{2}{n_{in}+n_{out}} \]

3.6 优化算法

优化算法

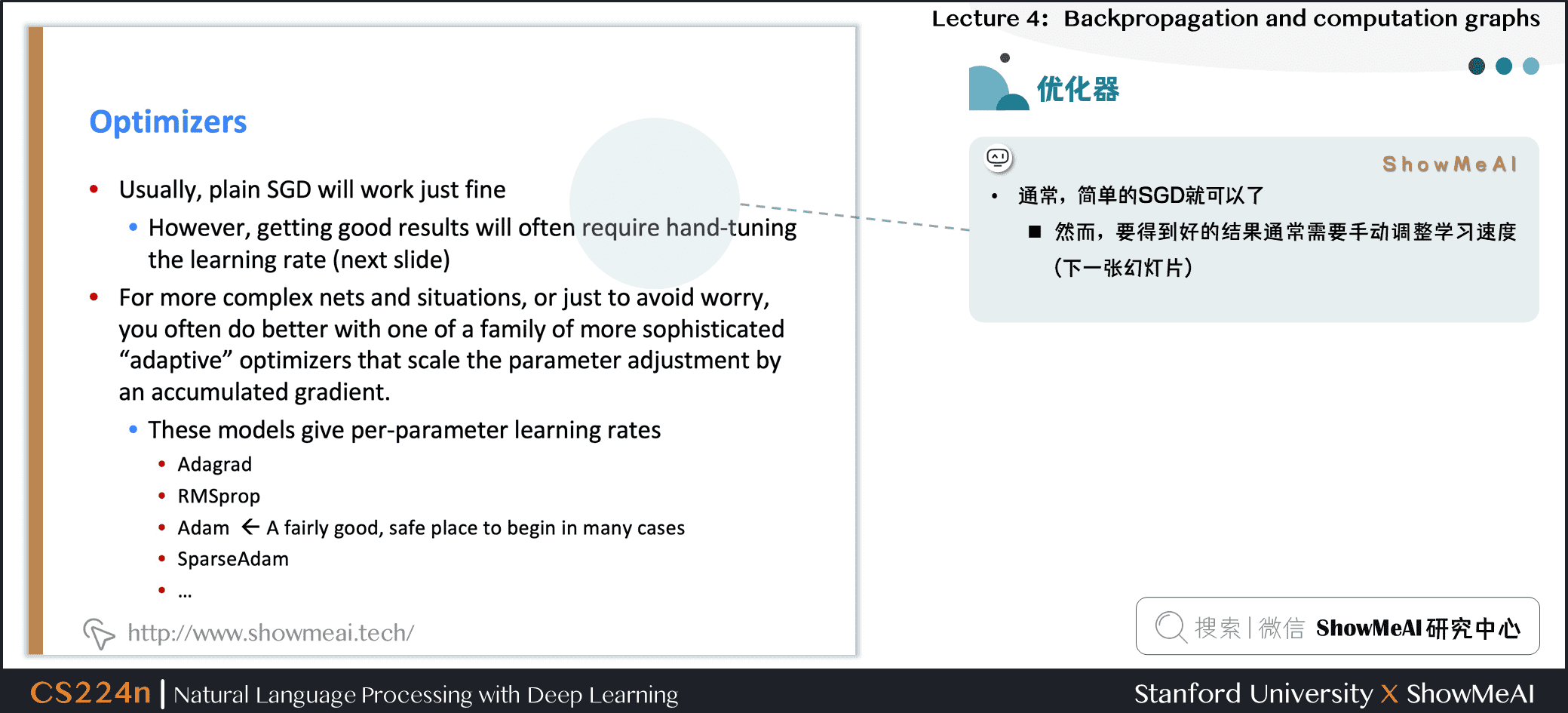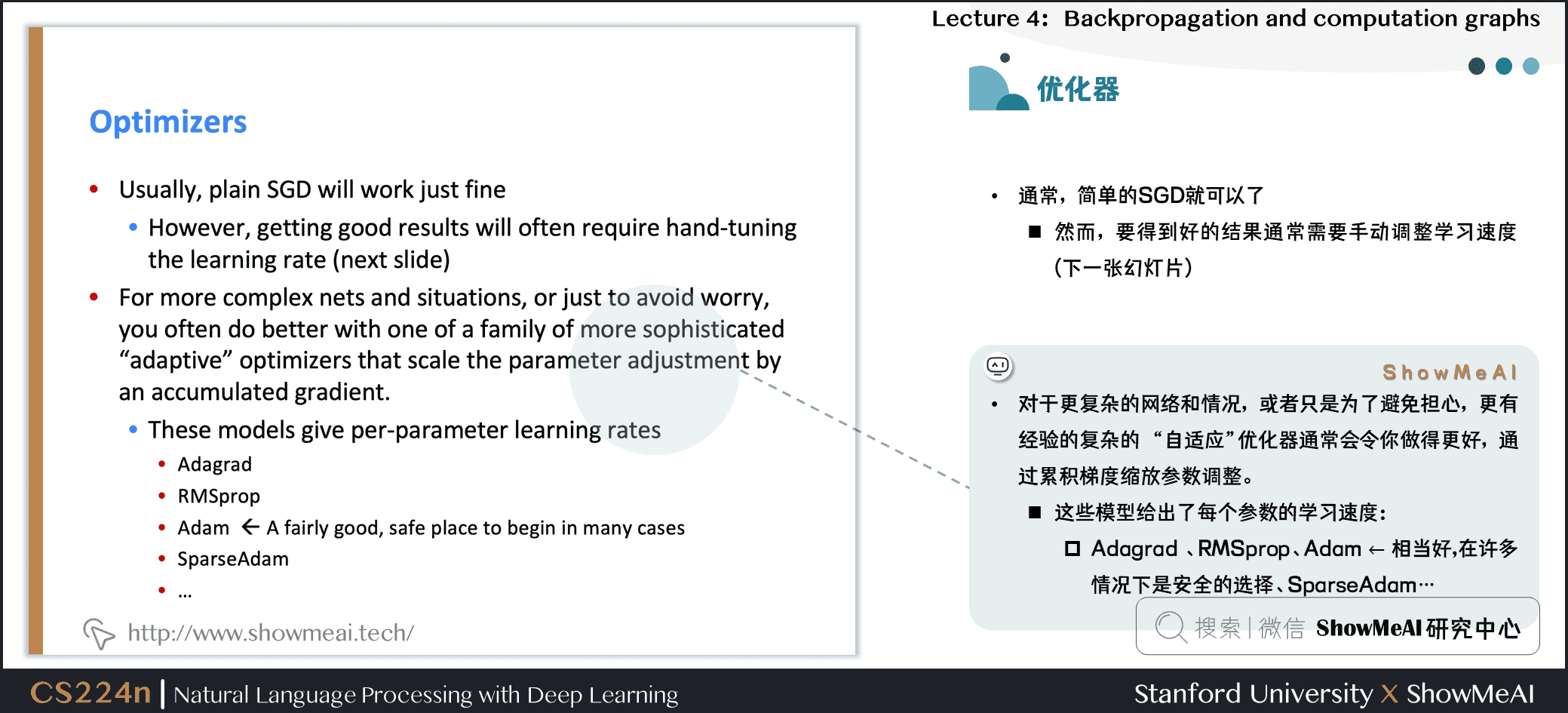
通常，简单的SGD就可以了

  • 然而，要得到好的结果通常需要手动调整学习速度(下一张幻灯片)
  • 对于更复杂的网络和情况，或者只是为了避免担心，更有经验的复杂的 “自适应”优化器通常会令你做得更好，通过累积梯度缩放参数调整。
  • 这些模型给每个参数调整学习速度
    • Adagrad
    • RMSprop
    • Adam 相当好,在许多情况下是安全的选择
    • SparseAdam
    • …

3.7 学习率策略

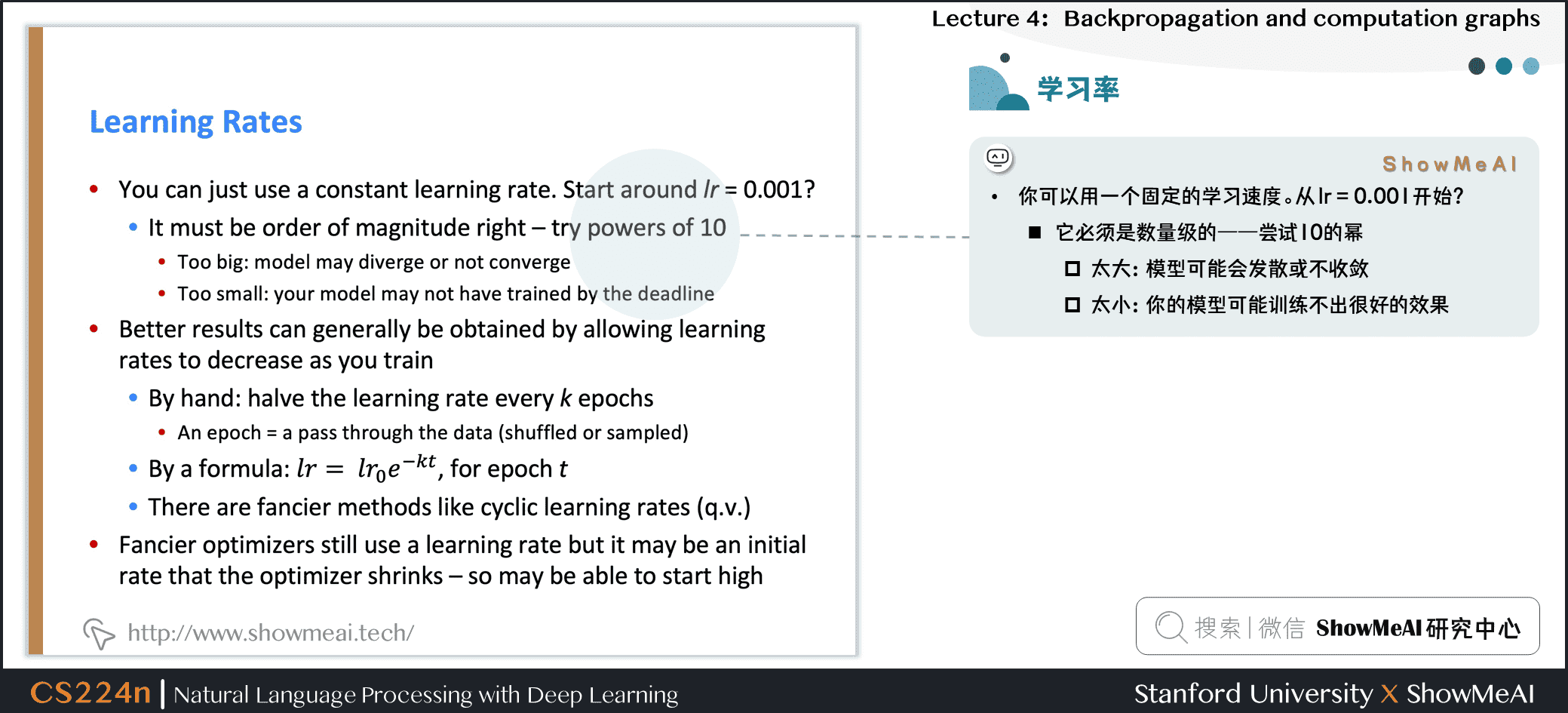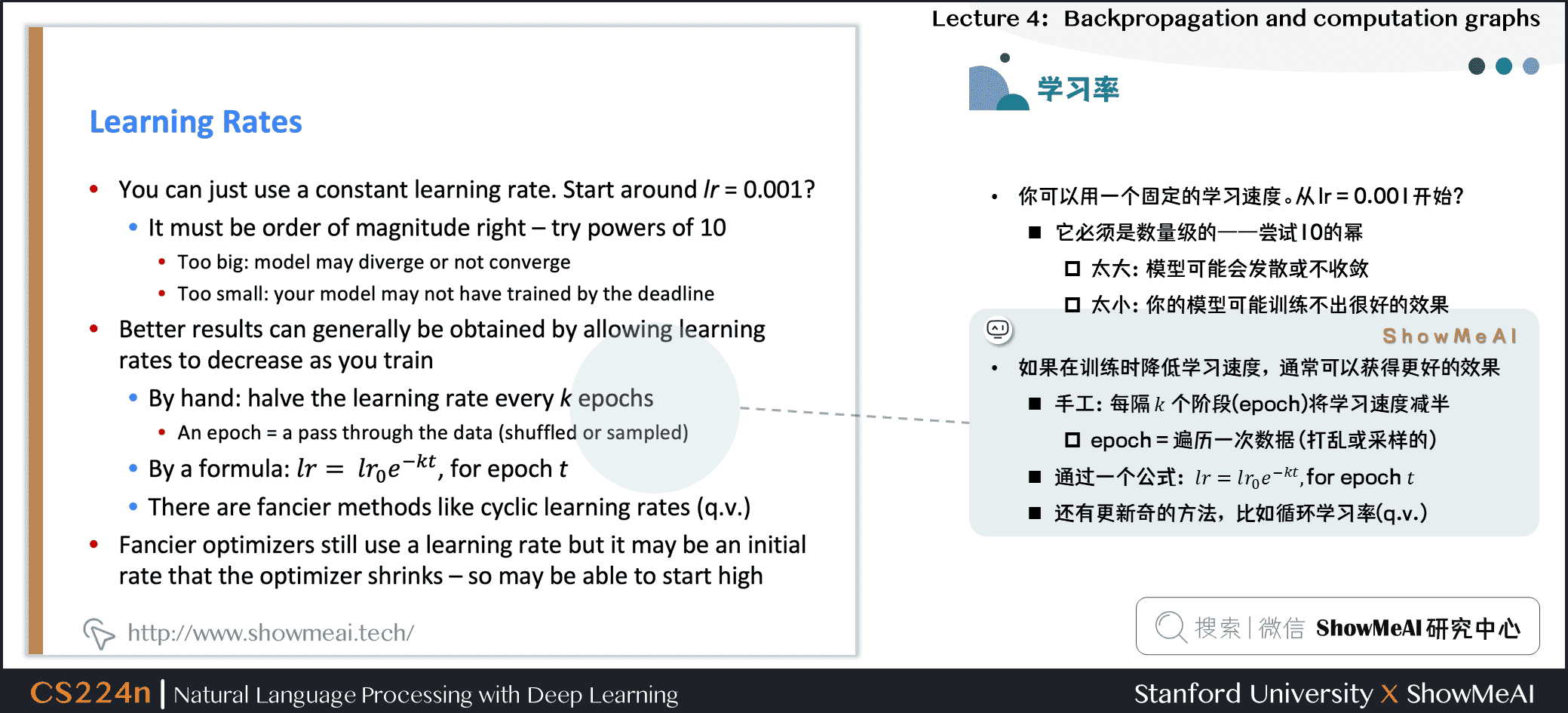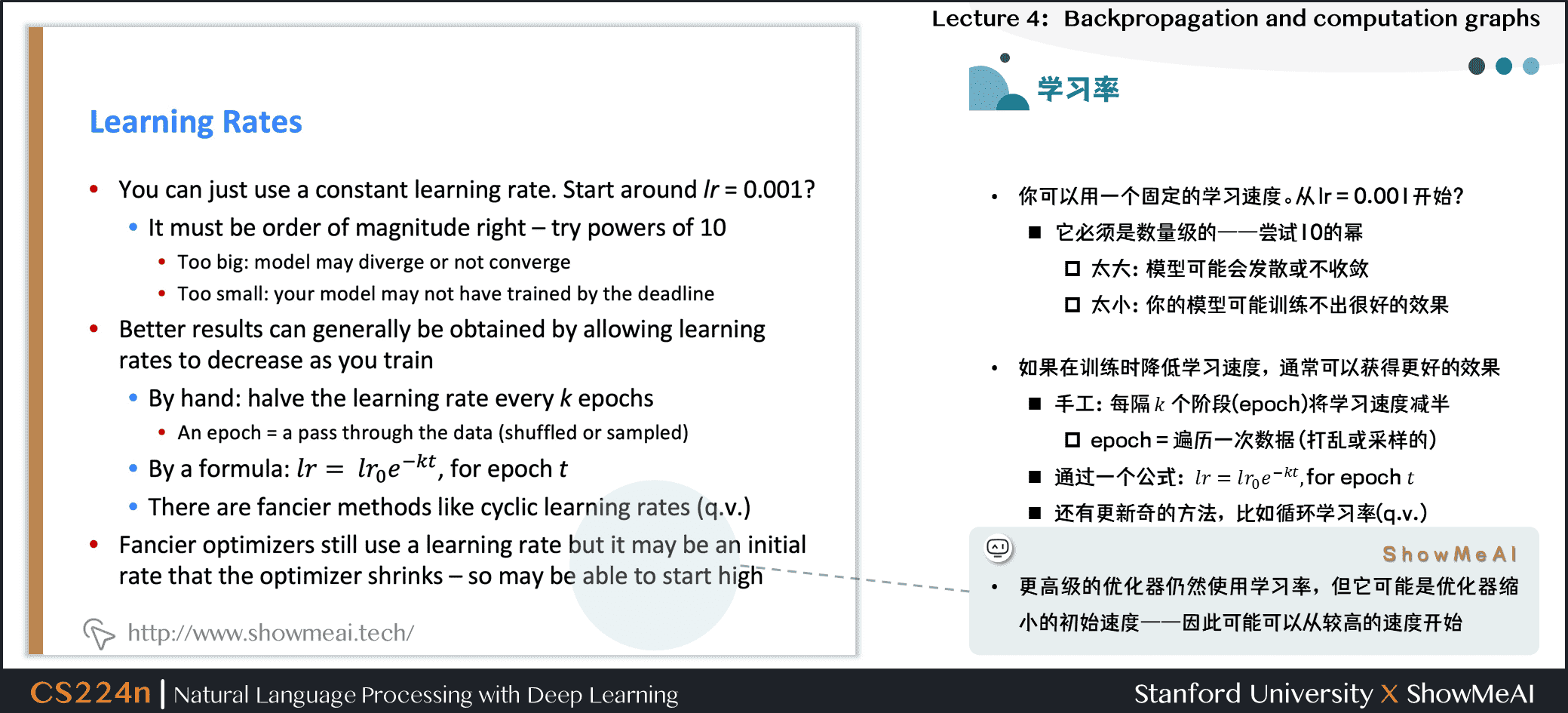
学习率策略

  • 你可以用一个固定的学习速度。从 \(lr = 0.001\)开始？

    • 它必须是数量级的——尝试10的幂
    • 太大：模型可能会发散或不收敛
    • 太小：你的模型可能训练不出很好的效果

  • 如果你在训练时降低学习速度，通常可以获得更好的效果

    • 手工：每隔 \(k\) 个阶段(epoch)将学习速度减半
      • epoch = 遍历一次数据 (打乱或采样的)
    • 通过一个公式： \(l r=l r_{0} e^{-k t}\), {for epoch }t
    • 还有更新奇的方法，比如循环学习率(q.v.)

  • 更高级的优化器仍然使用学习率，但它可能是优化器缩小的初始速度——因此可能可以从较高的速度开始

4.视频教程

可以点击 B站 查看视频的【双语字幕】版本

5.参考资料

ShowMeAI系列教程推荐

自然语言处理 (NLP) 教程

斯坦福 CS224n 课程带学详解

ShowMeAI用知识加速每一次技术成长

posted @ 2022-05-04 00:10  ShowMeAI  阅读(136)  评论(0)  编辑  收藏  举报