大厂技术实现 | 多目标优化及应用（含代码实现）@推荐与计算广告系列

💡 作者：韩信子@ShowMeAI
📘 大厂解决方案系列教程：https://www.showmeai.tech/tutorials/50
📘 本文地址：https://www.showmeai.tech/article-detail/60
📢 声明：版权所有，转载请联系平台与作者并注明出处
📢 收藏 ShowMeAI 查看更多精彩内容

---

一图读懂全文

本篇内容使用到的数据集为 🏆2021微信大数据挑战赛数据集，大家可以通过 ShowMeAI 的百度网盘地址快速下载。数据集和代码的整理花费了很多心思，欢迎大家 PR 和 Star！

🏆 大厂技术实现的数据集下载（百度网盘）：公众号『ShowMeAI研究中心』回复『大厂』，或者点击 这里 获取本文 多目标优化及应用（含代码实现） 『2021微信大数据挑战赛数据集』

⭐ ShowMeAI官方GitHub（实现代码）：https://github.com/ShowMeAI-Hub/multi-task-learning

---

一、多目标优化介绍

1.1 什么是多目标优化场景

多目标排序是推荐排序系统中常见的技术实现，在很多推荐与排序常见中，有多个业务目标，找到一种综合排序方法使得多个目标都达到整体最优，能有最好的总体收益。

1.2 为什么需要多目标优化

为什么需要多目标排序呢，在实际互联网的推荐系统产品中，大多数用户反馈都不是直接评分，而是各式各样的隐式反馈，比如说用户的点击、收藏、分享、观看时长、下单购买等。 在评估用户满意度与设定优化目标时，可能有一些偏差：

• 全局偏差/Global bias：不同目标表达不同的偏好程度。
  • 电商场景中，购买行为表达的偏好高于点击浏览和收藏
  • 新闻场景中，浏览时长超过20s这个行为表达的偏好高于点击
  • 短视频场景，完播行为表达的偏好高于点击
• 物品偏差/Item bias：单个目标衡量不全面。
  • 信息流产品中，标题党增加点击率，但降低满意度
  • 短视频场景中，悬念设计提升完播率，但需要观看下一个引发用户更多操作的不满
  • 自媒体资讯产品，鼓励转发率，可能会提升『转发保平安』等恶性操作
• 用户偏差/User bias：⽤户表达满意度的方式不同
  • 信息流产品中，用户有 深度阅读、点赞、收藏 等不同表达满意的方式
  • 短视频场景中，用户有 点赞、收藏、转发 等不同表达满意的方式

下图为部分互联网产品下，用户包含信息反馈的行为路径。

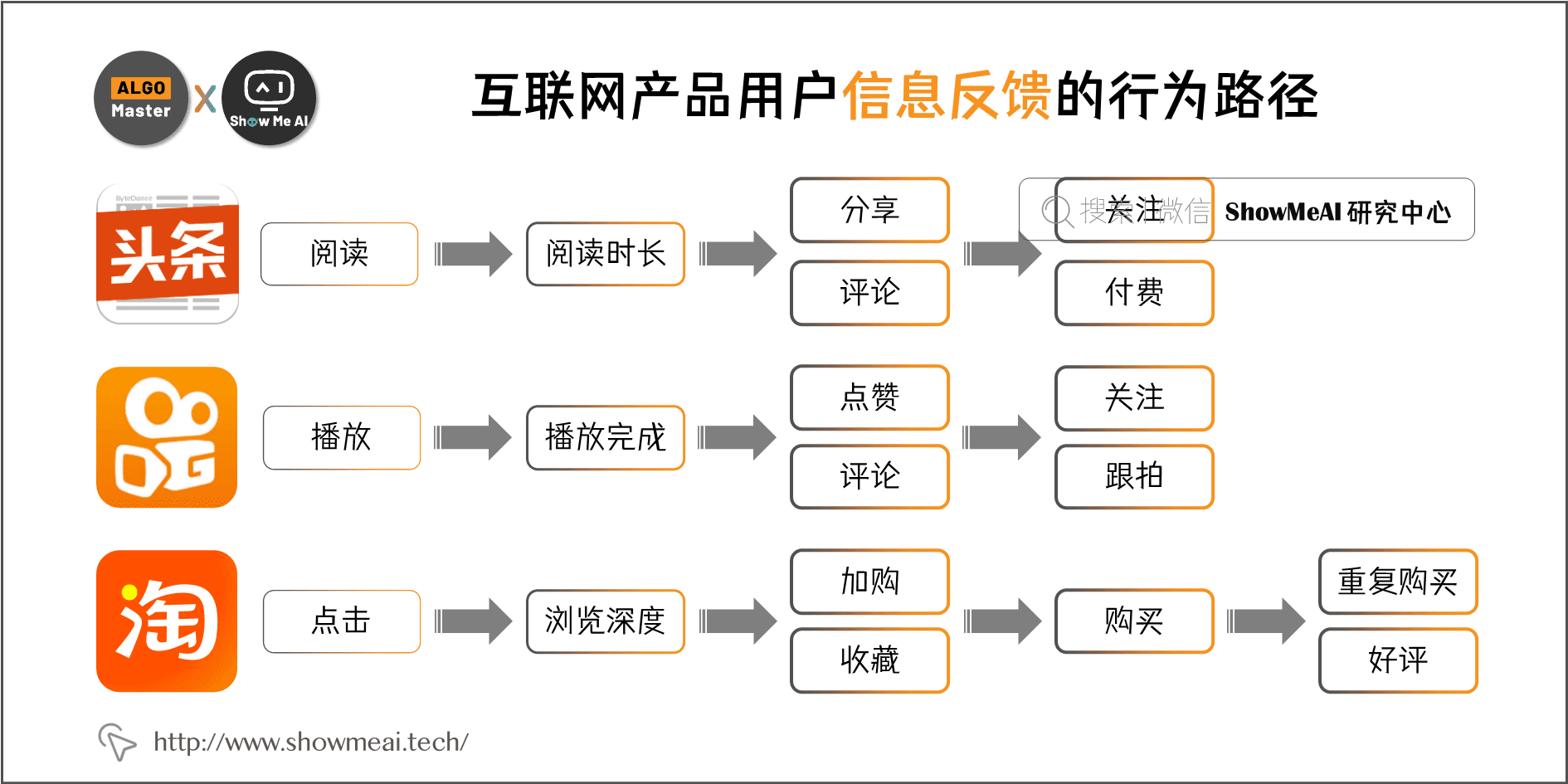
在上述众多互联网业务中，工程师优化和提升的目标可能是多个，比如，短视频推荐任务，既要点击率又要完播率；电商排序，既要点击率又要转化率。

1.3 多目标优化的难点

多目标优化的主要技术实现是在推荐系统的『排序』环节完成，如下所示的信息流推荐中，排序环节影响最终展示结果，进而对目标效果影响最为直接。

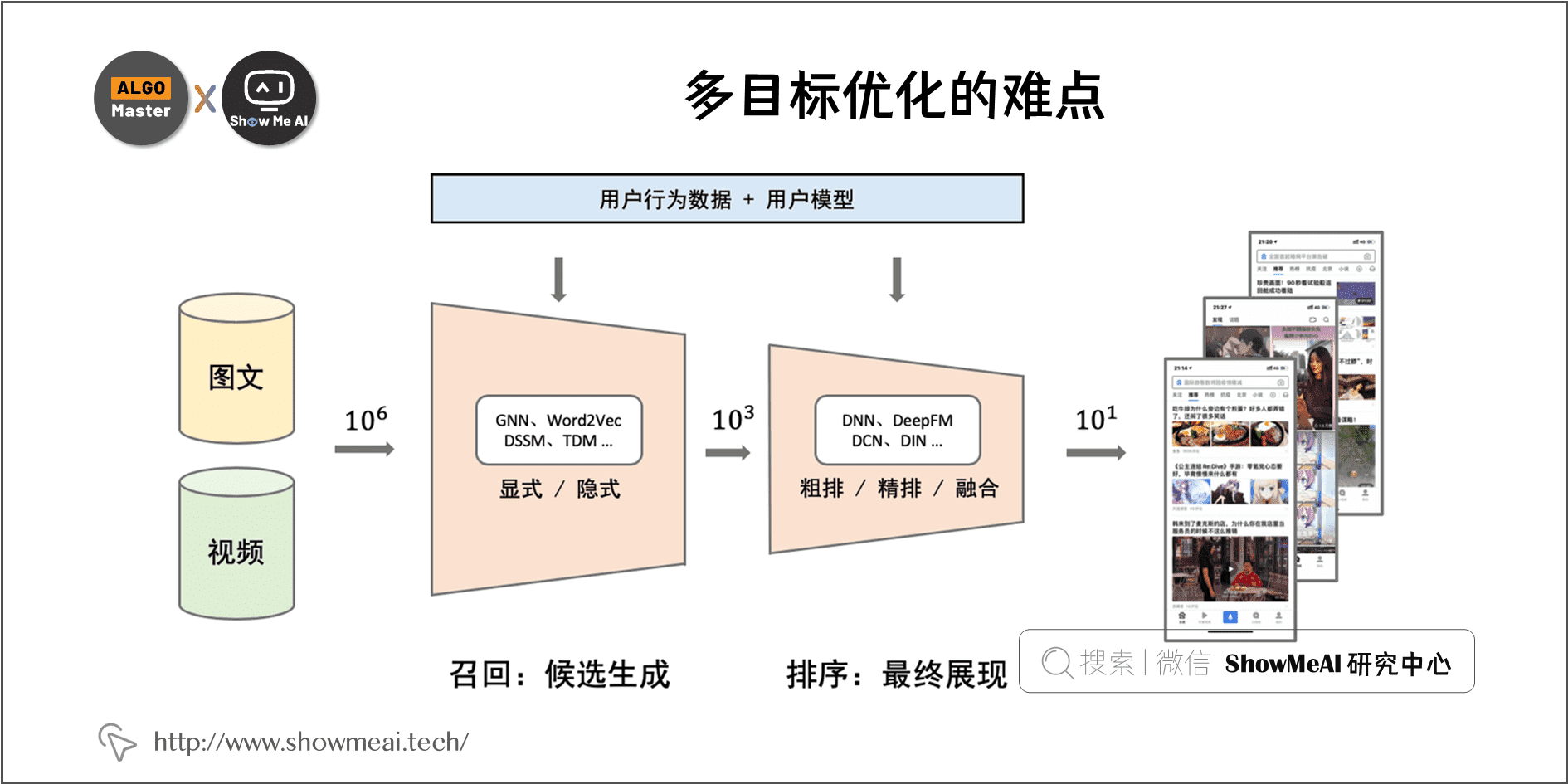
排序环节多使用 CTR 预估（click through rate prediction）技术来完成，业界有非常成熟的机器学习与深度学习技术方法与方案。但是，应用在多目标学习优化中，有五大难点：

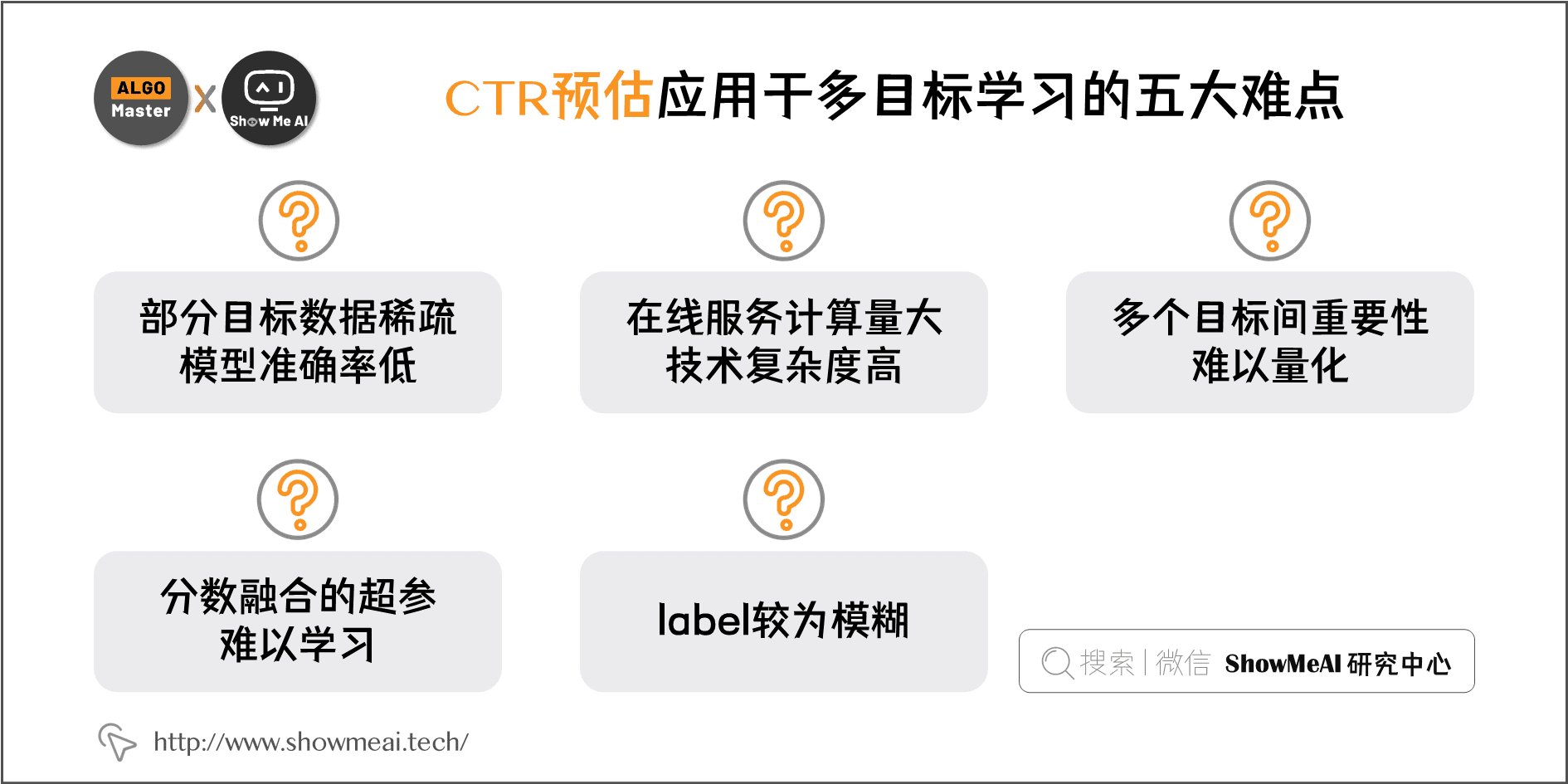
① 部分目标数据稀疏，模型准确率低。 比如在电商产品中，用户下单行为显著稀疏于点击行为，下单的标签正样本数量和比例都偏小
② 在线服务计算量⼤。 通常多目标优化的模型有着更为复杂的模型结构，在线预估时，计算复杂度也更高；实时推荐任务需要有短响应时间和高并发支撑的稳定性，技术复杂度高一些。
③ 多个目标间重要性难以量化。 在追求点击率又追求完播率的短视频中，这两个target如何量化权衡重要度？
④ 分数融合的超参难以学习。 很多建模方案中，我们会量化得到不同的目标score，但最终融合时，涉及到的融合计算超参数不容易通过业务直接敲定，也没有合适的方法让模型学习
⑤ Label较为模糊。 很多业务中，连标签本身也是模糊的，比如资讯类产品中的阅读时长多长算长?

1.4 多目标vs多任务

实际技术解决方案中，有几个非常相似的概念，分别是 多任务、多目标、多类别，他们的定义和关联如下图所示：

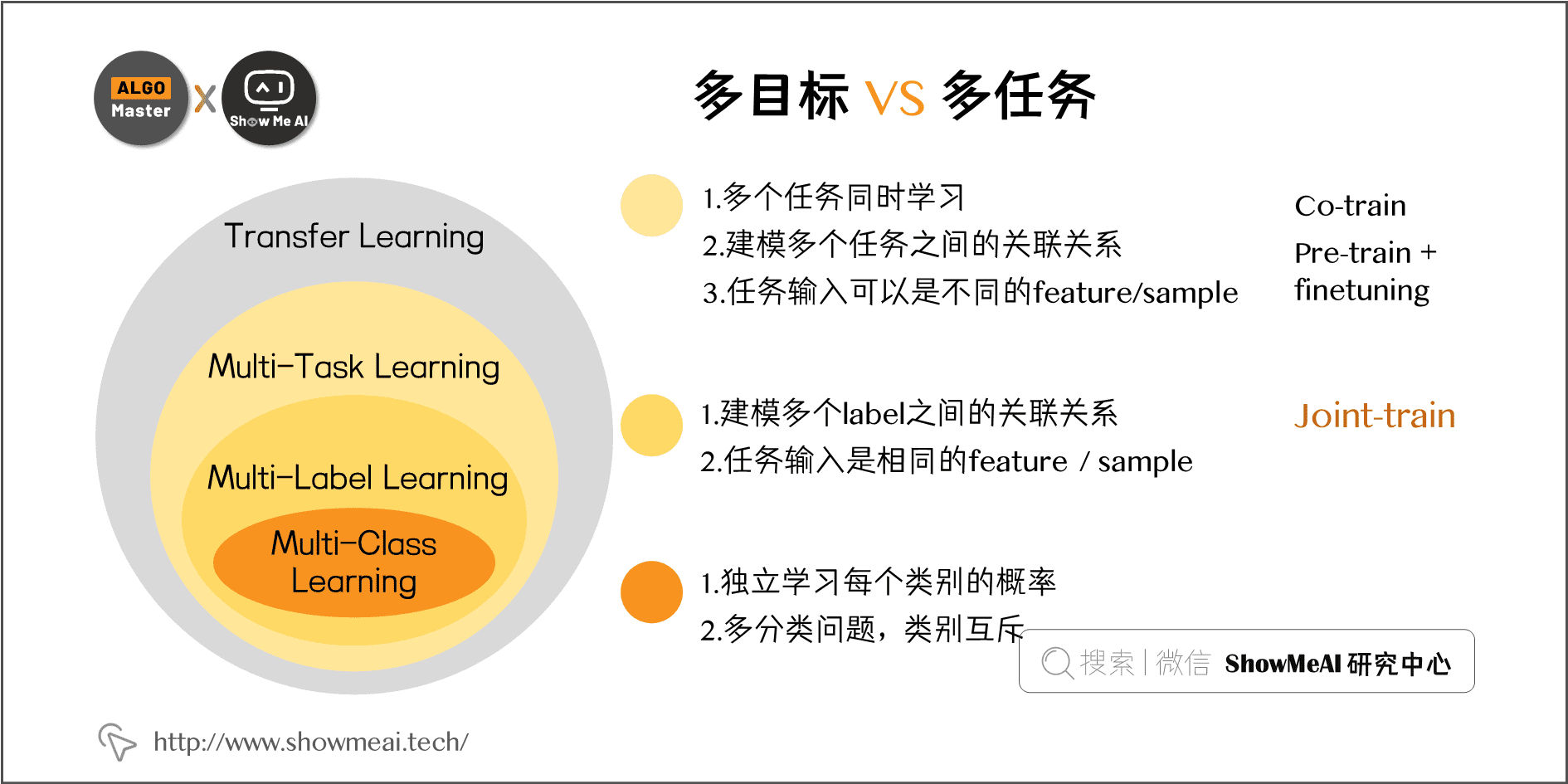
在我们这里提到的推荐多目标优化中，其实不同的目标也对应不同的 task。 比如电商场景下，在推荐的排序阶段进行 CTR 建模，对同一输入样本同时预估点击率、转化率多个目标，在这个场景下，我们认为多目标多任务优化可以采用同一套方法。

我们经常使用联合训练 Joint-train 的模式进行多目标优化学习，公式如下：

\[L=\min _{\theta} \sum_{t=1}^{T} \alpha^{t} L^{t}\left(\theta^{s h}, \theta^{t}\right) \]

• \(\theta^{t}\) 是任务 \(t\) 的独享参数，总 \(Loss\) 是每个子任务对应 \(Loss\) 的带权求和。

二、多目标学习与共享参数

多任务多目标学习的实现，我们现在多采用『共享』机制完成，可以在不同任务的模型参数和特征共享两方面做设计。

• 模型架构方面：在深度学习网络中可以共享 embedding 特征，或者共享中间层的某些隐藏单元，也可以是模型某一层或者最后一层的结果，并且共享之外的部分各自独立。在模型的设计中，层间关系自由组合搭配。
• 特征组合方面：多个任务可以采用不同的特征组合，有的特征只属于模型架构的某个部分，有些特征整个模型都可以使用。

2.1 典型的一些参数共享机制

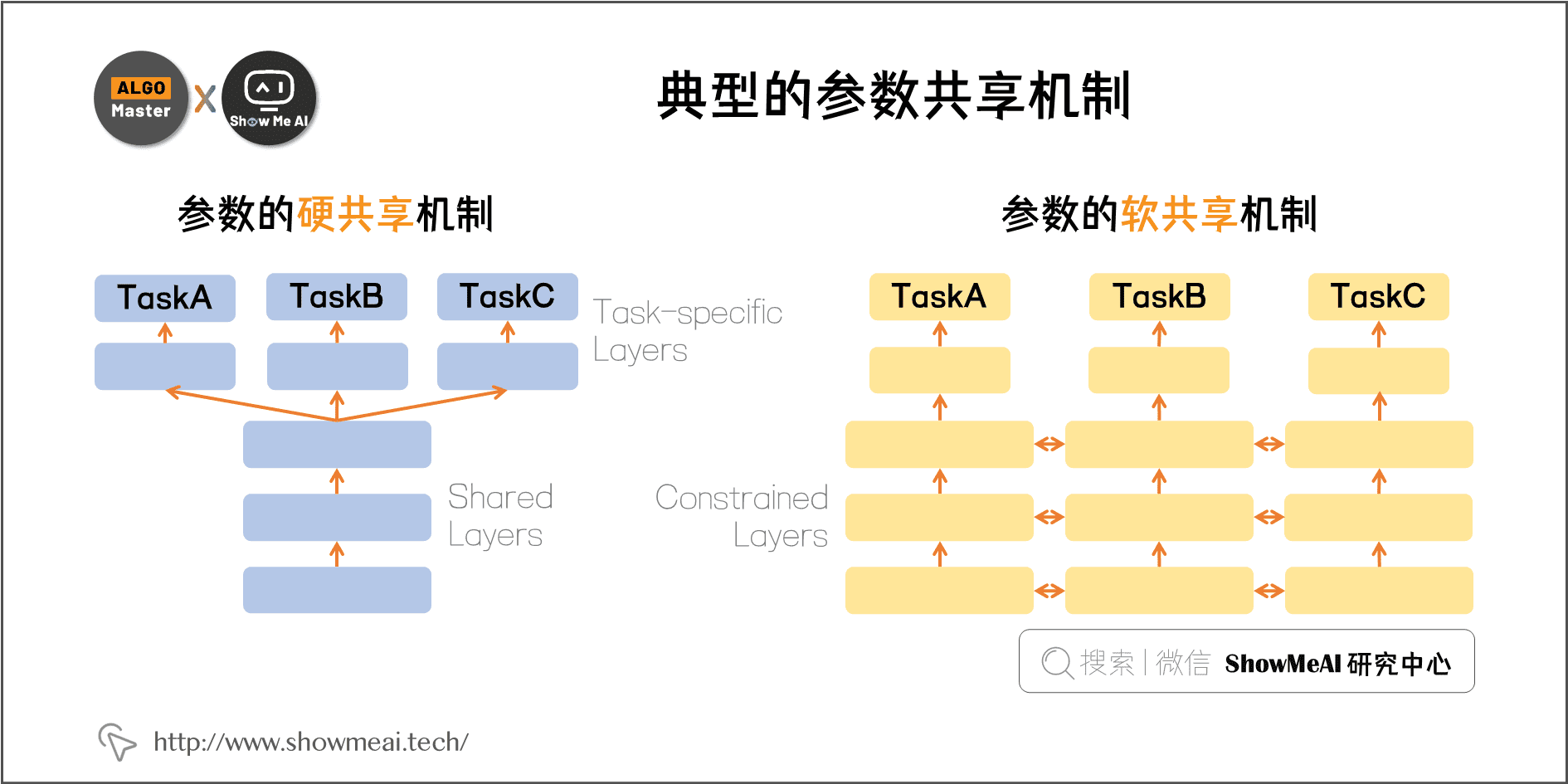
① 参数的硬共享机制 （基于参数的共享，Parameter Based）

基于参数的共享是多目标学习最常用的方法。在深度学习的网络中，通过共享特征和特征的embedding以及隐藏层的网络架构，在最后一层通过全连接+softmax的方式来区分不同任务，最后做一个线性融合来实现多目标排序。

② 参数的软共享机制 （基于约束的共享，Regularization Based）

参数的软共享机制，每个任务都有自己的参数和模型结构，可以选择哪些共享哪些不共享。最后通过正则化的方式，来拉近模型参数之间的距离，例如使用 L2 进行正则化。

2.2 多目标优化的4种结果

实际多目标优化，在采用共享机制设计的各种模型结构后，可能有『Well Done』、『还不错』、『不理想』、『无法接受』 这 \(4\) 种不同的结果：

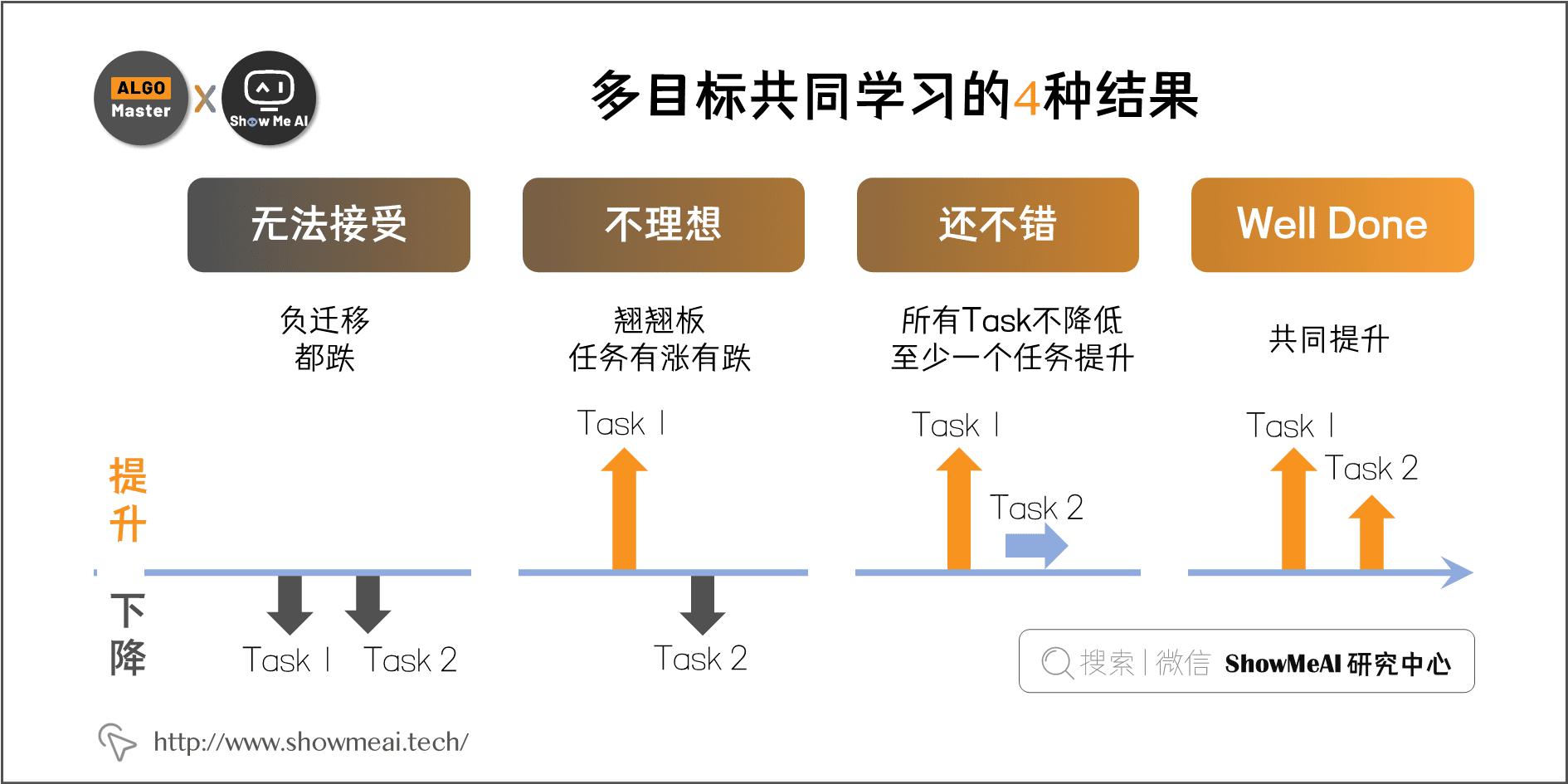
• 『Well Done』：最好的状态，所有share任务实现共同提升。
• 『还不错』：其次的状态，所有任务不降低，至少一个任务提升。如果是 主任务 + 辅助任务 的搭配，能够实现牺牲辅助任务达到主任务提升的效果，也是 well done。
• 『不理想』：跷跷板现象，任务有涨有跌。
• 『无法接受』：负迁移现象，所有任务都不如从前。

三、多目标学习两大优化方向

为了能够更好地『共享参数』，让同个模型中多个任务和谐共存、相辅相成、相得益彰，研究界有两大优化方向，分别是：

① 网络结构优化，设计更好的参数共享位置与方式

② 优化策略提升，设计更好的优化策略以提升优化 \(Loss\) 过程中的多任务平衡
​

优化方向1：网络结构设计。网络结构设计方向思考哪些参数共享，在什么位置，如何共享等。

优化方向2：优化方法与策略。多目标优化策略从loss与梯度的视角去思考任务与任务之间的关系。平衡loss体量（Magnitude），调节loss更新速度（velocity），优化Gradient更新方向（direction）。在微观层面缓解梯度冲突，参数撕扯，在宏观层面达到多任务的平衡优化。

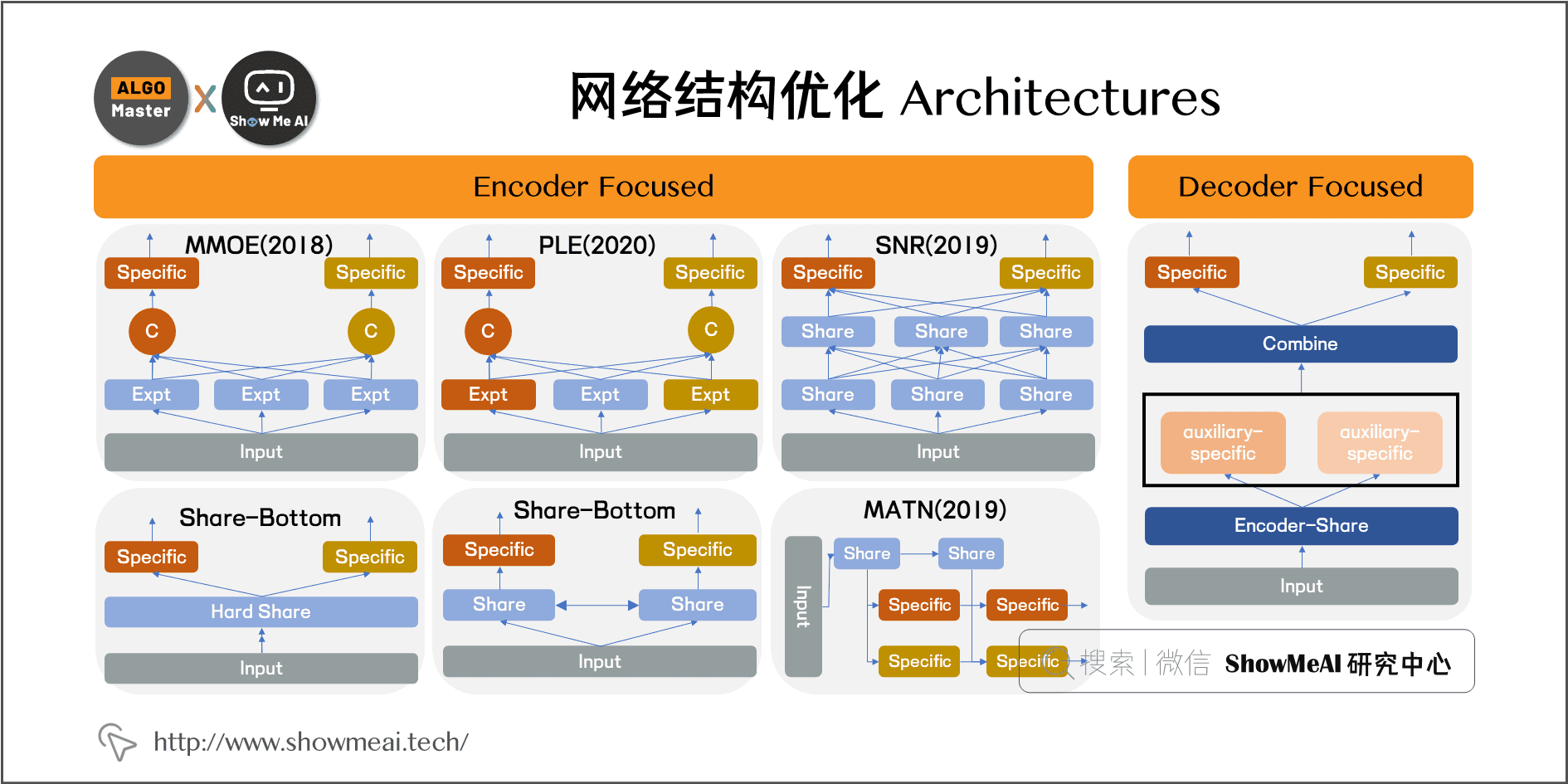
四、优化方向1：网络结构优化

4.1 总体思想与演进思路

网络结构设计是目前多任务研究和应用的主要焦点，它主要思考哪些参数共享，在什么位置，如何共享。优秀合理的共享网络结构对于最终效果提升作用巨大。

近年来网络结构设计经历了 Share Bottom \(\to\) MMoE \(\to\) PLE 的典型结构变迁，重要的业界顶尖企业研究人员发表的多任务网络结构设计论文包括：

• Share Bottom：早期一直在使用的方式，参数共享（hard或者soft）的方式来对多任务建模。
• 2018 Google MMOE：将hard的参数共享变成多个 expert，通过门控来控制不同loss对每个expert的影响。
• 2019 Google SNR：借助简单的 NAS（Neural Architecture Search），对 Sub-Network 进行组合，为不同目标学习各自的网络结构。
• 2020 腾讯 PLE：在 MMOE 的基础上增加了各任务独有的 Expert。

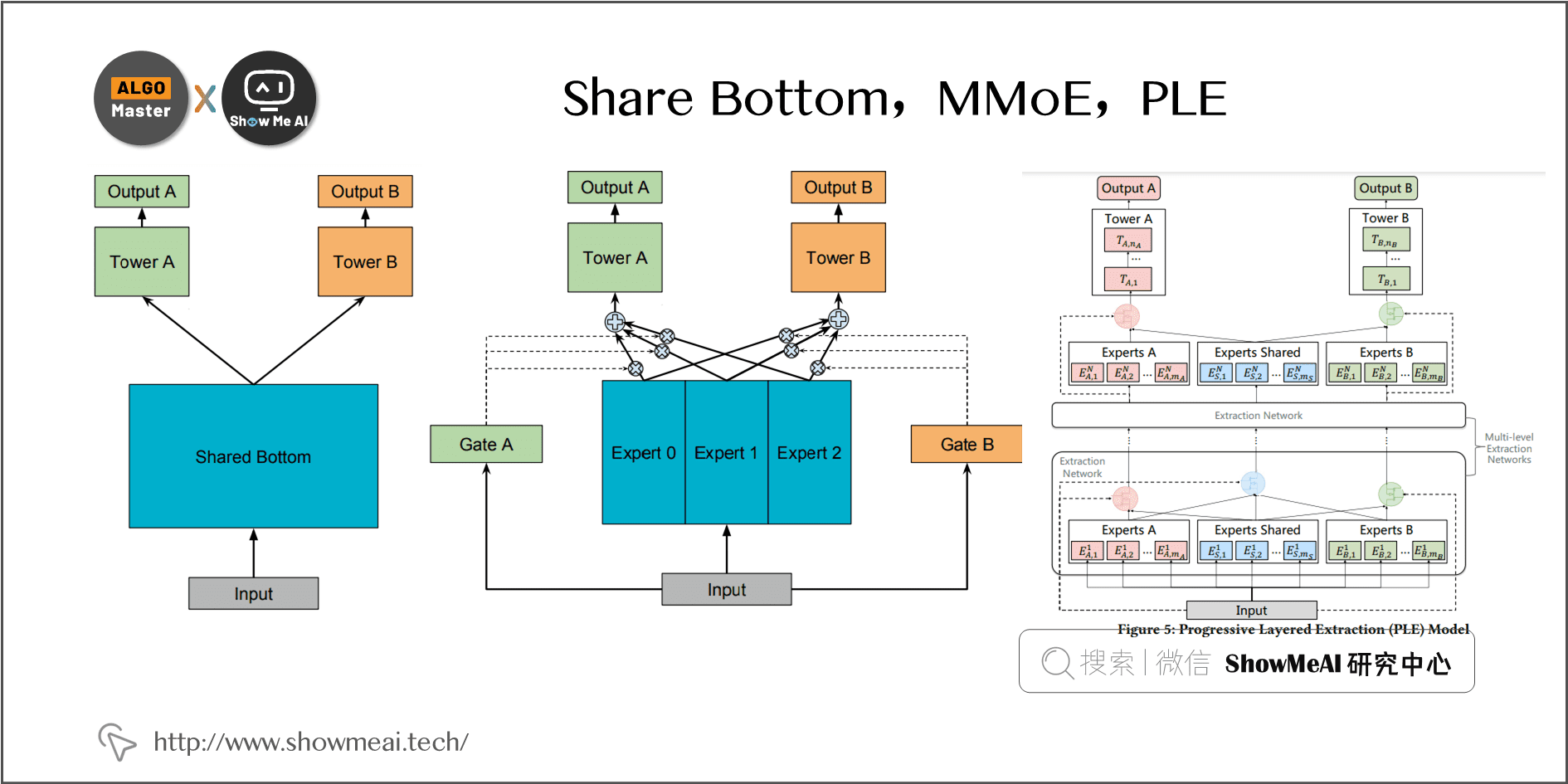
下图中对早期的 Share Bottom，MMoE，PLE 三种典型网络结构及对应的动机和公式做了总结。

• Shared Bottom \(\to\) MMoE：MMoE将 Shared Bottom分解成多个 Expert，然后通过门控网络自动控制不同任务对这些Expert的梯度贡献。
• MMoE \(\to\) PLE：PLE 在 MMoE 的基础上又为每个任务增加了自有的 Expert，仅由本任务对其梯度更新。

4.2 核心论文与典型网络结构

我们来具体看一下论文中典型的网络结构：

1）MMoE：Google KDD 2018，现CTR建模多任务学习标配 [1]

Google《Modeling task relationships in multi-task learning with multi-gate mixture-of-experts》提出的 MMoE 几乎成为各家互联网公司做多任务多目标学习排序的标配结构。 在 Google 这篇 paper 中，研究人员通过人工控制两个任务的相似度，测试和研究不同网络结构的表现效果。

MMoE 结构设计中的 Multi-gate 对于任务差异带来的冲突有一定的缓解作用，即使在多任务之间的的相关性不高的情况下，也有不错的效果。 MMoE 中不同的 expert 负责学习不同的信息内容，然后通过 gate 来组合这些信息，通过不同任务 gate 的 softmax 的热力分布差异，来表明expert对不同的目标各司其责，从而提升了效果。

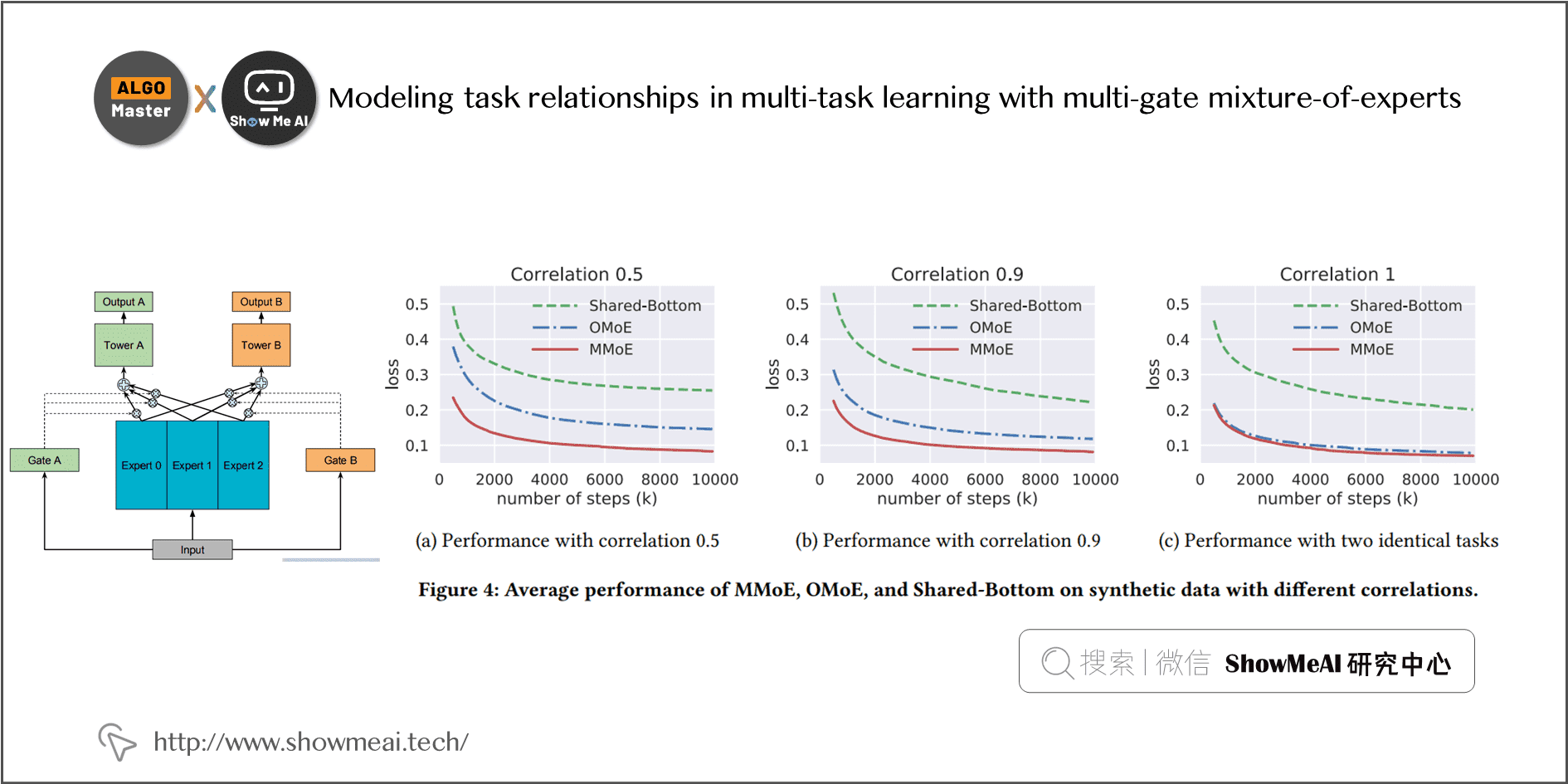
论文中大规模推荐系统数据集实验结果如下，MMoE 相对于 share bottom 的方式，各指标都有明显的提升：

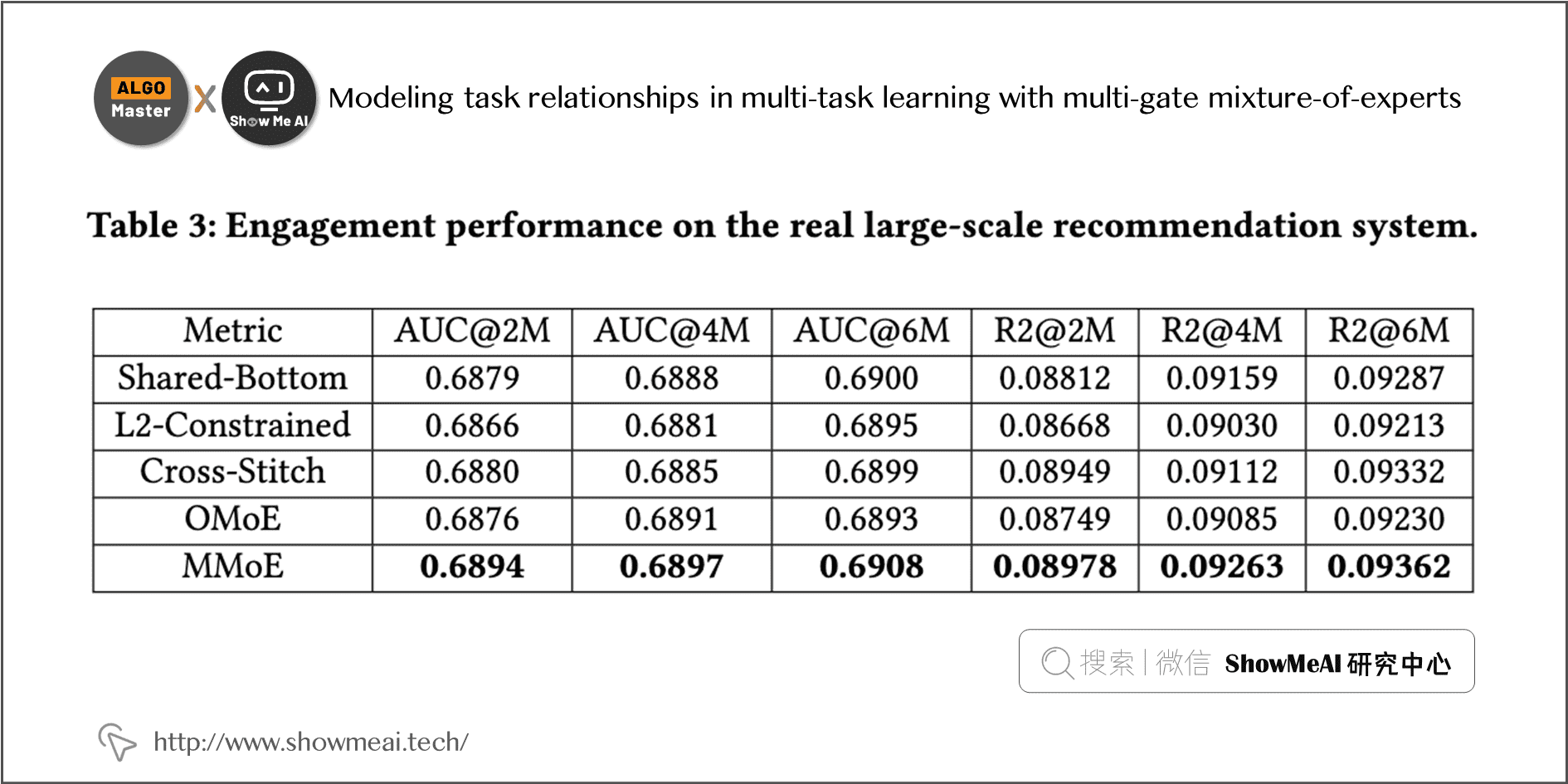
MMoE核心代码参考：

class MMoE_Layer(tf.keras.layers.Layer):
    def __init__(self,expert_dim,n_expert,n_task):
        super(MMoE_Layer, self).__init__()
        self.n_task = n_task
        self.expert_layer = [Dense(expert_dim,activation = 'relu') for i in range(n_expert)]
        self.gate_layers = [Dense(n_expert,activation = 'softmax') for i in range(n_task)]
    
    def call(self,x):
        # 构建多个专家网络
        E_net = [expert(x) for expert in self.expert_layer]
        E_net = Concatenate(axis = 1)([e[:,tf.newaxis,:] for e in E_net]) # 维度 (bs,n_expert,n_dims)
        # 构建多个门网络
        gate_net = [gate(x) for gate in self.gate_layers]     # 维度 n_task个(bs,n_expert)
        
        # towers计算：对应的门网络乘上所有的专家网络
        towers = []
        for i in range(self.n_task):
            g = tf.expand_dims(gate_net[i],axis = -1)  # 维度(bs,n_expert,1)
            _tower = tf.matmul(E_net, g,transpose_a=True)
            towers.append(Flatten()(_tower))           # 维度(bs,expert_dim)
​
        return towers

2）SNR：Google AAAI 2019，对MMoE的改进工作 [2]

Google 这篇《SNR: Sub-Network Routing forFlexible Parameter Sharing in Multi-Task Learning》paper 的思路与网络自动搜索（NAS）接近，通过动态学习产出多任务各自采用的 sub-network。研究思路是希望在更相似的任务下能学习到共享多一些的结构。

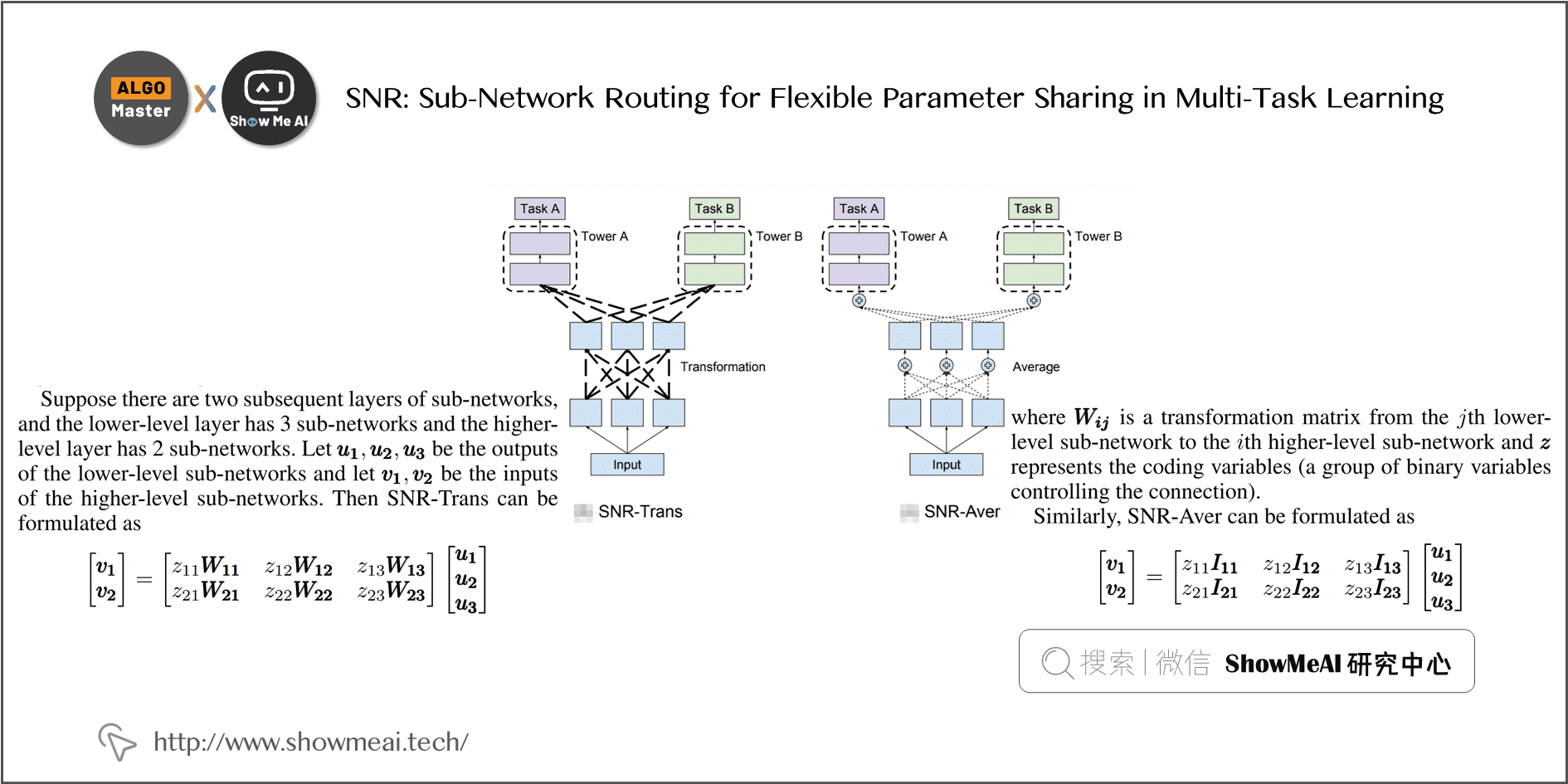
3）PLE ：腾讯 RecSys 2020, 改进MMoE，结构简单效果好 [3]

腾讯这篇《Progressive layered extraction (ple): A novel multi-task learning (mtl) model for personalized recommendations》paper 提出 PLE，主要是在 MMoE 的基础上，为每个任务增加了自己的 specific expert，仅由本任务对其梯度更新。

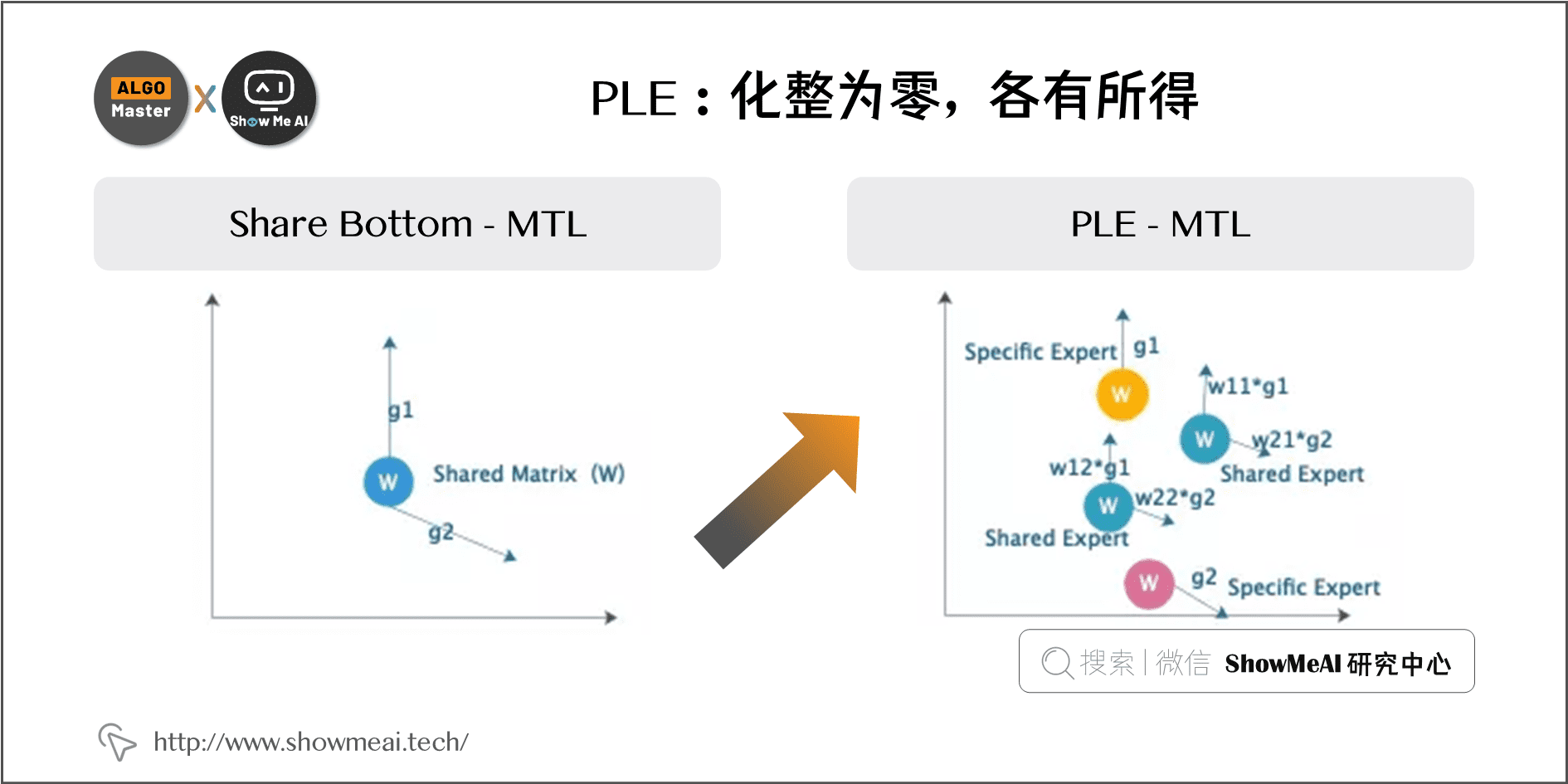
如下图所示，在 Share Bottom 的结构上，整个共享参数矩阵如同质量较大的物体，在梯度更新的环节，两个 \(Loss\) 反向计算的梯度向量分别是 \(g_1\) 和 \(g_2\)，是这个物体受到的两个不同方向不同大小的力，这两个力同时来挪动这个物体的位置，如果在多次更新中两个力大概率方向一致，那么就能轻松达到和谐共存、相辅相成。反之，多个力可能出现彼此消耗、相互抵消，那么任务效果就会大打折扣。

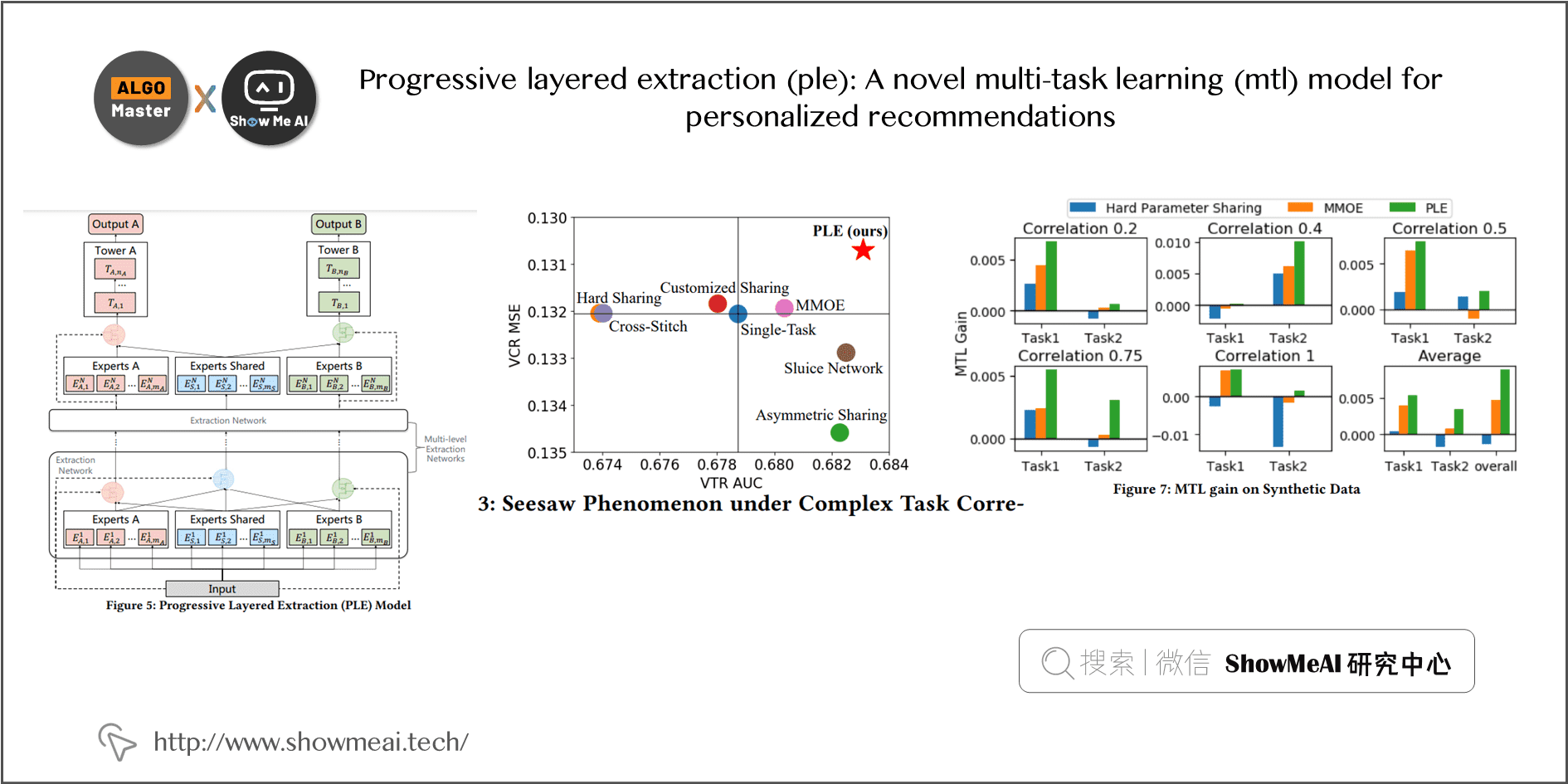
MMoE 通过『化整为零』，把一个共享参数矩阵化成多个结合 gate 的共享 Expert，这样不同的loss在存在相互冲突的时候，在不同的 expert 上，不同 \(Loss\) 可以有相对强弱的表达，那么出现相互抵消的情况就可能减少，呈现出部分 experts 受某 task 影响较大，部分 experts 受其他 task 主导，形成『各有所得』的状态。而 PLE 增加了spcific experts，能进一步保障『各有所得』，保证稳定优化。

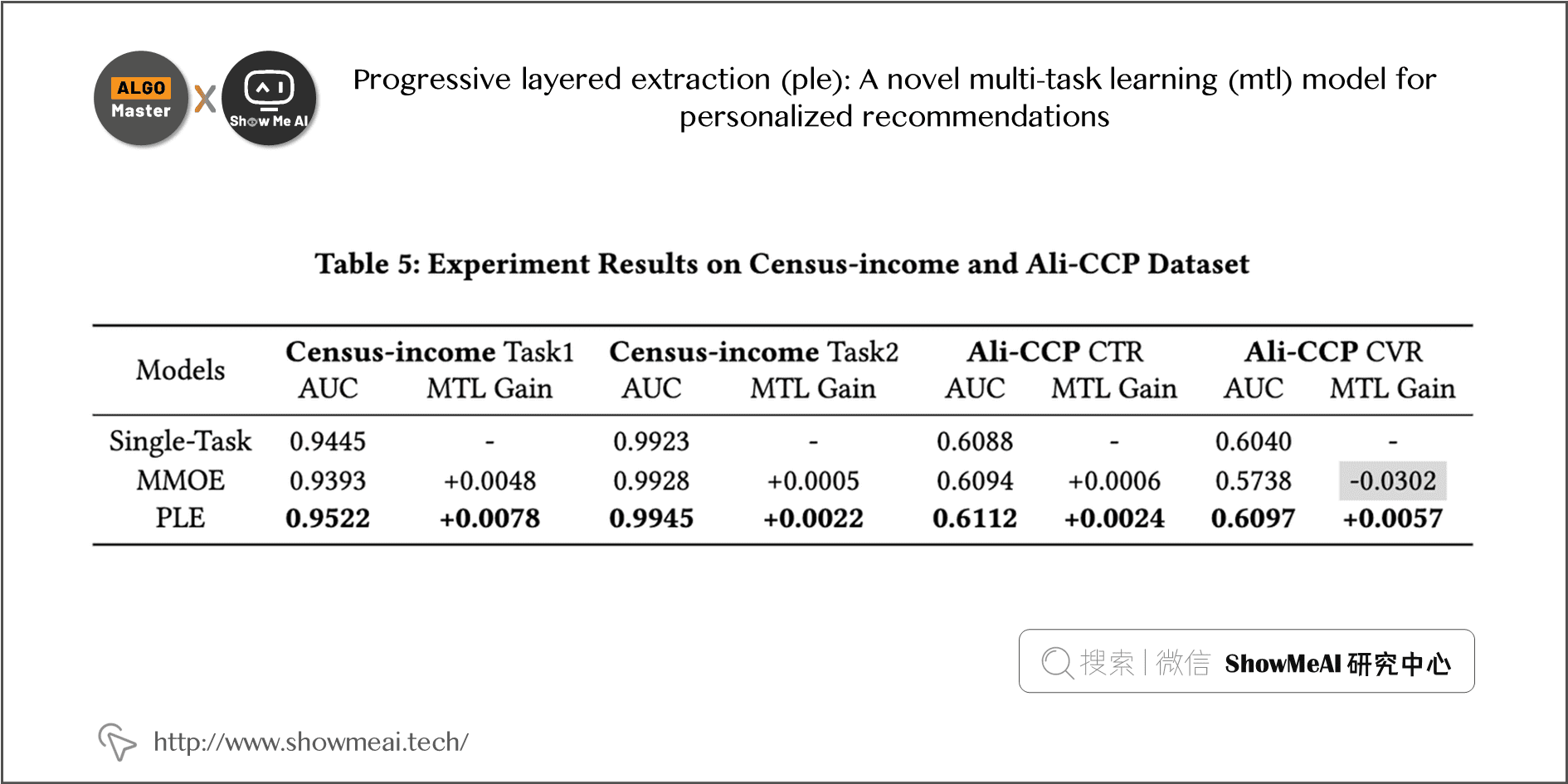
最终的paper实验结果如下：

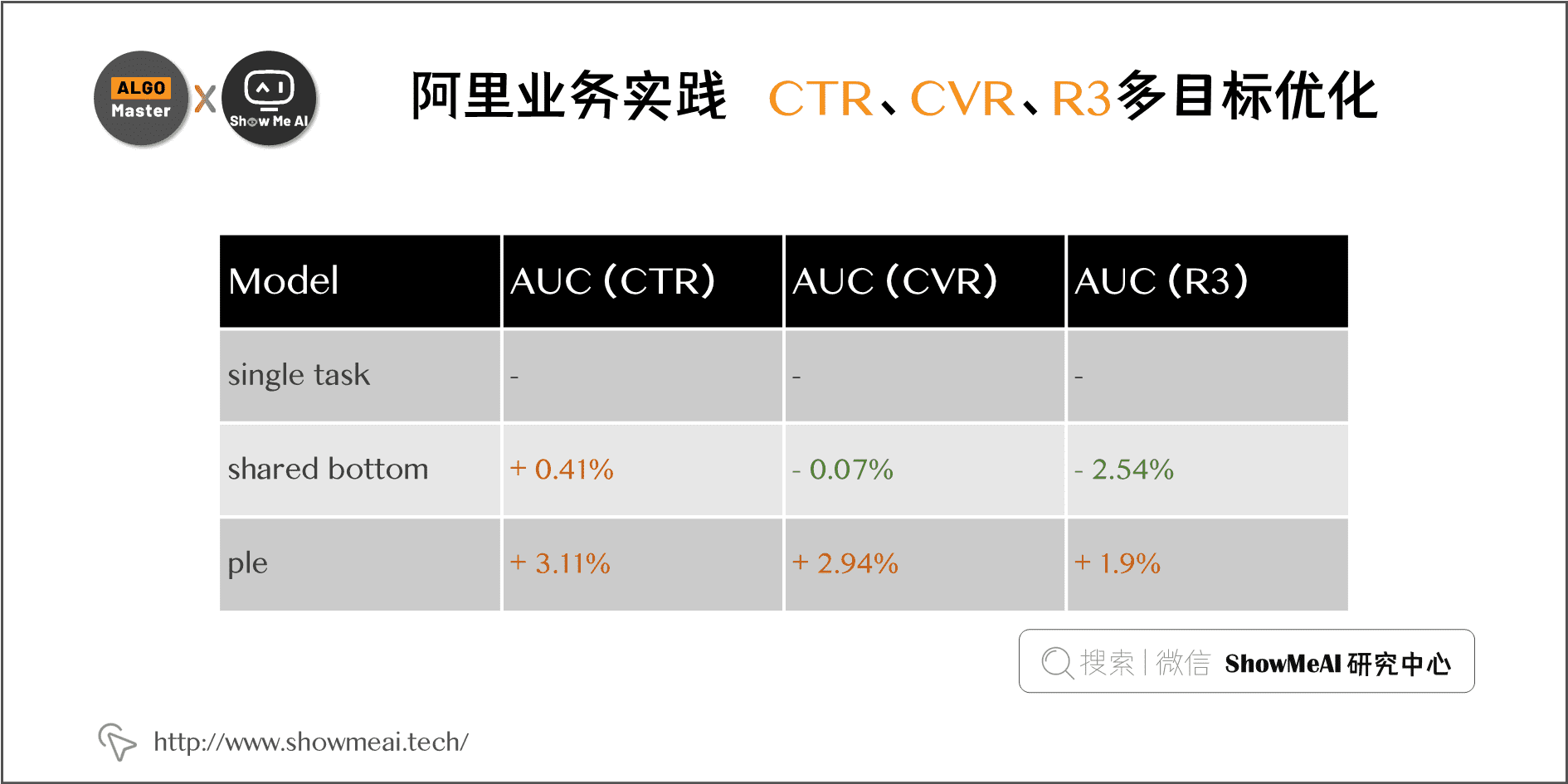
阿里的业务下，对 CTR、CVR、R3 这3个指标进行多目标优化，对于 single task 的相对提升结果如下表。其中 Share-Bottom 出现了翘翘板现象，而 PLE 实现了多目标共赢的结果。

PLE核心代码参考：

class PleLayer(tf.keras.layers.Layer):
    '''
    @param n_experts: list,每个任务使用几个expert。[3,4]第一个任务使用3个expert，第二个任务使用4个expert。
    @param n_expert_share: int,共享的部分设置的expert个数。
    @param expert_dim: int,每个专家网络输出的向量维度。
    @param n_task: int,任务个数。
    '''
    def __init__(self,n_task,n_experts,expert_dim,n_expert_share,dnn_reg_l2 = 1e-5):
        super(PleLayer, self).__init__()
        self.n_task = n_task
        
        # 定义多个任务特定网络和1个共享网络
        self.E_layer = []
        for i in range(n_task):
            sub_exp = [Dense(expert_dim,activation = 'relu') for j in range(n_experts[i])]
            self.E_layer.append(sub_exp)
            
        self.share_layer = [Dense(expert_dim,activation = 'relu') for j in range(n_expert_share)]
        # 定义门控网络
        self.gate_layers = [Dense(n_expert_share+n_experts[i],kernel_regularizer=regularizers.l2(dnn_reg_l2),
                                  activation = 'softmax') for i in range(n_task)]
​
    def call(self,x):
        # 特定网络和共享网络
        E_net = [[expert(x) for expert in sub_expert] for sub_expert in self.E_layer]
        share_net = [expert(x) for expert in self.share_layer]
        
        # 【门权重】和【指定任务及共享任务输出】的乘法计算
        towers = []
        for i in range(self.n_task):
            g = self.gate_layers[i](x)
            g = tf.expand_dims(g,axis = -1) #维度 (bs,n_expert_share+n_experts[i],1)
            _e = share_net+E_net[i]  
            _e = Concatenate(axis = 1)([expert[:,tf.newaxis,:] for expert in _e]) #维度 (bs,n_expert_share+n_experts[i],expert_dim)
            _tower = tf.matmul(_e, g,transpose_a=True)
            towers.append(Flatten()(_tower)) #维度 (bs,expert_dim)
        return towers

​

五、优化方向2：优化方法与策略

5.1 总体思想与演进思路

优化方法更多的考虑的是在已有结构下，更好地结合任务进行训练和参数优化，它从 \(Loss\) 与梯度的维度去思考不同任务之间的关系。在优化过程中缓解梯度冲突，参数撕扯，尽量达到多任务的平衡优化。

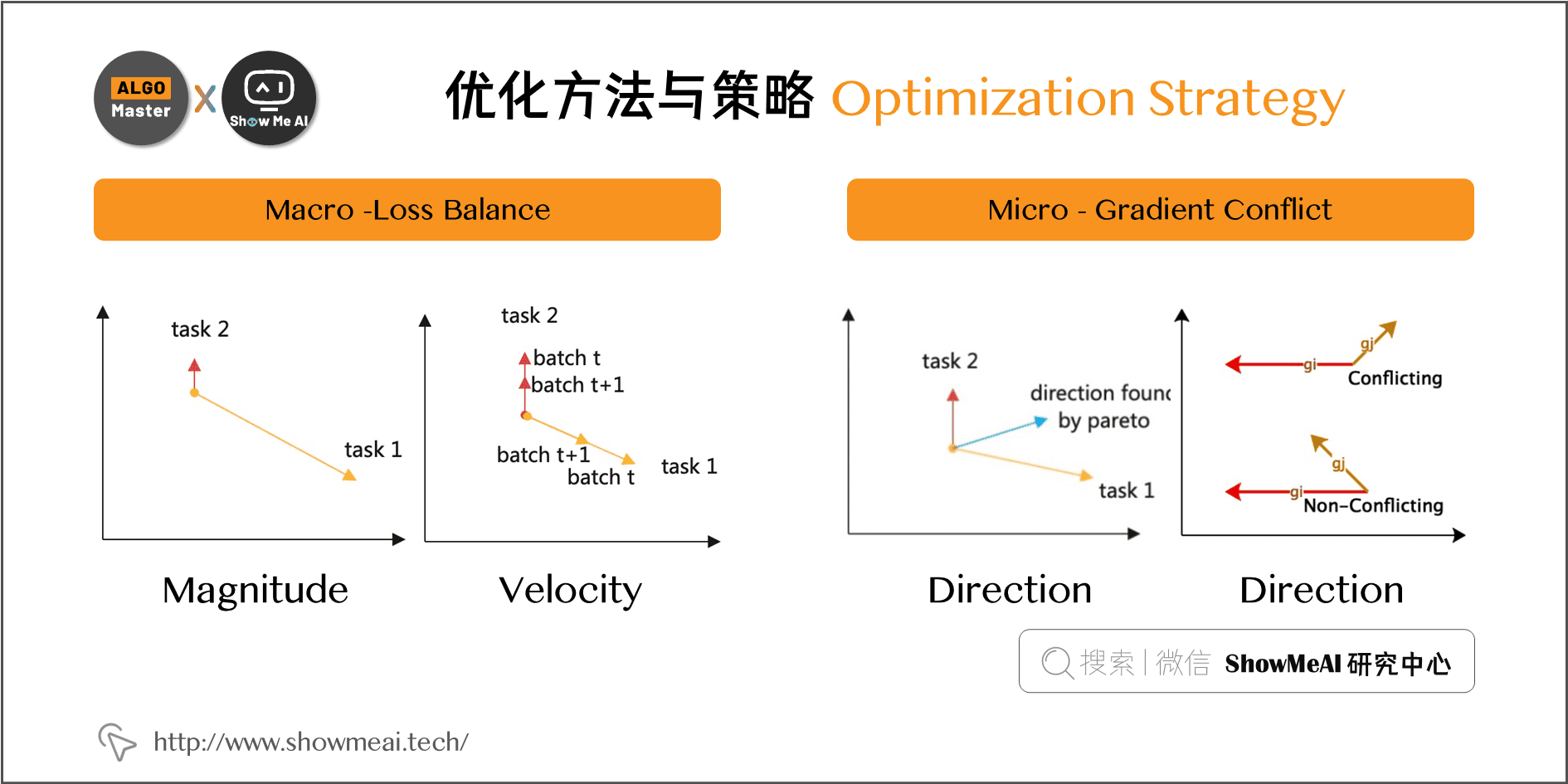
目前各式各样的多任务多目标优化方法策略，主要集中在3个问题：

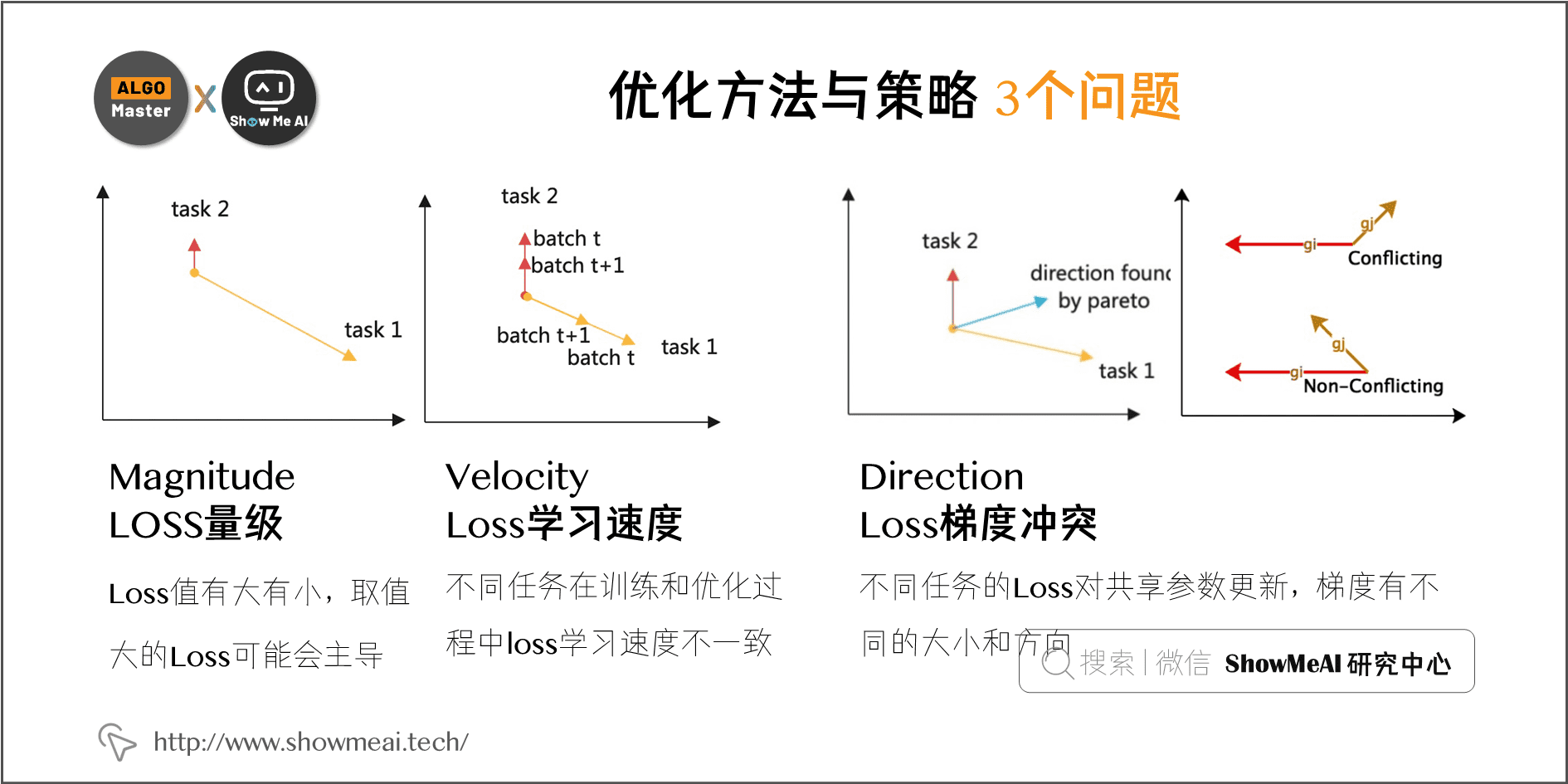
1）Magnitude（Loss量级）

\(Loss\) 值有大有小，取值大的 \(Loss\) 可能会主导，如图所示，需要处理这个问题。典型的例子是二分类任务 + 回归任务的多目标优化，L2 \(Loss\) 和交叉熵损失的 \(Loss\) 大小与梯度大小的量级和幅度可能差异很大，如果不处理会对优化造成很大干扰。

2）Velocity （Loss学习速度）

不同任务因为样本的稀疏性、学习的难度不一致，在训练和优化过程中，存在 \(Loss\) 学习速度不一致的情况。如果不加以调整，可能会出现某个任务接近收敛甚至过拟合的时候，其他任务还是欠拟合的状态。

3）Direction（Loss梯度冲突）

不同任务的 \(Loss\) 对共享参数进行更新，梯度存在不同的大小和方向，相同参数被多个梯度同时更新的时候，可能会出现冲突，导致相互消耗抵消，进而出现跷跷板、甚至负迁移现象。 这也是核心需要处理的问题。

5.2 核心论文与典型方法介绍

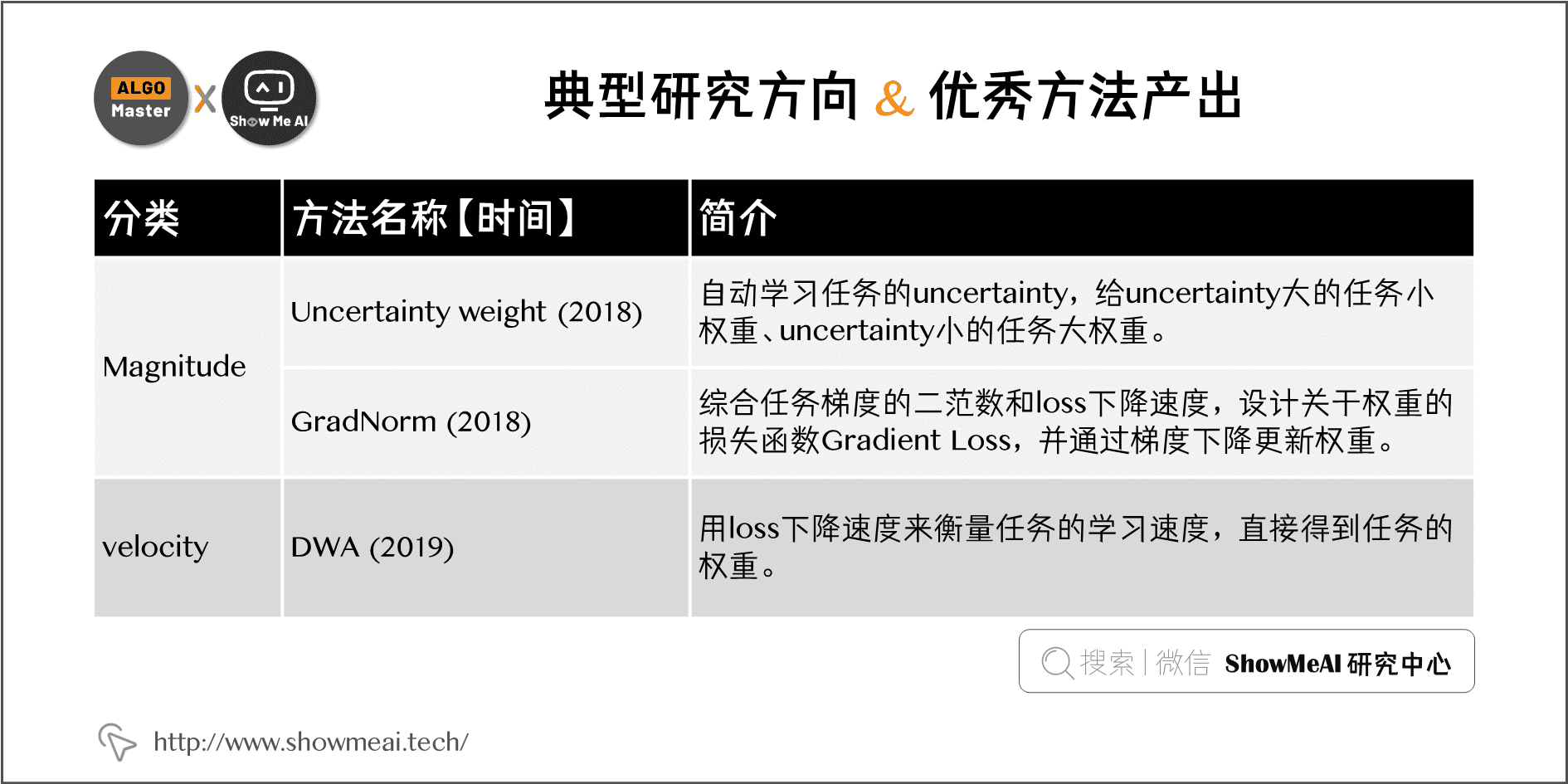
针对上述3大核心问题，近年来典型的研究子方向和优秀的产出方法如下图表：

1）Uncertainty Weight [4]

简单的多任务学习往往是把所有 \(Loss\) 进行联合优化，通常需要需要手动调节他们的 weights。典型的 \(Loss\) Function 如下：

\[L_{\text {total }}=\sum_{i} w_{i} L_{i} \]

然而这种方式通常存在如下问题：

模型最后学习效果对于 weights 非常敏感，否则很难同时收获对于多个任务都比较优的模型。同时手工调节这些 weights 也是非常费时费力的工作。 这篇 paper 提出直接建模单个任务中的 uncertainty，然后通过 uncertainty 来指导权重的调节。

\[\mathcal{L}\left(W, \sigma_{1}, \sigma_{2}\right) \approx \frac{1}{2 \sigma_{1}^{2}} \mathcal{L}_{1}(W)+\frac{1}{2 \sigma_{2}^{2}} \mathcal{L}_{2}(W)+\log \sigma_{1}+\log \sigma_{2} \]

为直接建模的uncertainty，是一个可学习的参数。 总 \(Loss\) 设计成这样的形式，模型优化过程中会倾向于惩罚高 \(Loss\) 而低 \(\sigma\) 的情况（如果一个任务的 \(Loss\) 高，同时 \(\sigma\) 又小的话，这一项就会很大，优化算法就会倾向于优化它）。

背后的含义是： \(Loss\) 大的任务，包含的uncertainty也应该多，而它的权重就应该小一点。 这样优化的结果就是往往 \(Loss\) 小（『相对简单』）的任务会有一个更大的权重。例如在分类 + 回归的多目标优化任务中，回归任务 \(Loss\) 大，Uncertainty Weight 给予小权重，整体效果可能是有帮助的。

Uncertainty Weight核心代码参考：

from keras.layers import Input, Dense, Lambda, Layer
from keras.initializers import Constant
from keras.models import Model
from keras import backend as K
​
# 自定义loss层
class CustomMultiLossLayer(Layer):
    def __init__(self, nb_outputs=2, **kwargs):
        self.nb_outputs = nb_outputs
        self.is_placeholder = True
        super(CustomMultiLossLayer, self).__init__(**kwargs)
        
    def build(self, input_shape=None):
        # 初始化 log_vars
        self.log_vars = []
        for i in range(self.nb_outputs):
            self.log_vars += [self.add_weight(name='log_var' + str(i), shape=(1,),
                                              initializer=Constant(0.), trainable=True)]
        super(CustomMultiLossLayer, self).build(input_shape)
​
    def multi_loss(self, ys_true, ys_pred):
        assert len(ys_true) == self.nb_outputs and len(ys_pred) == self.nb_outputs
        loss = 0
        for y_true, y_pred, log_var in zip(ys_true, ys_pred, self.log_vars):
            precision = K.exp(-log_var[0])
            loss += K.sum(precision * (y_true - y_pred)**2. + log_var[0], -1)
        return K.mean(loss)
​
    def call(self, inputs):
        ys_true = inputs[:self.nb_outputs]
        ys_pred = inputs[self.nb_outputs:]
        loss = self.multi_loss(ys_true, ys_pred)
        self.add_loss(loss, inputs=inputs)
        return K.concatenate(inputs, -1)

​

2）GradNorm [5]

Gradient normalization方法的主要思想是：

• 希望不同的任务的 \(Loss\) 量级是接近的
• 希望不同的任务以相似的速度学习

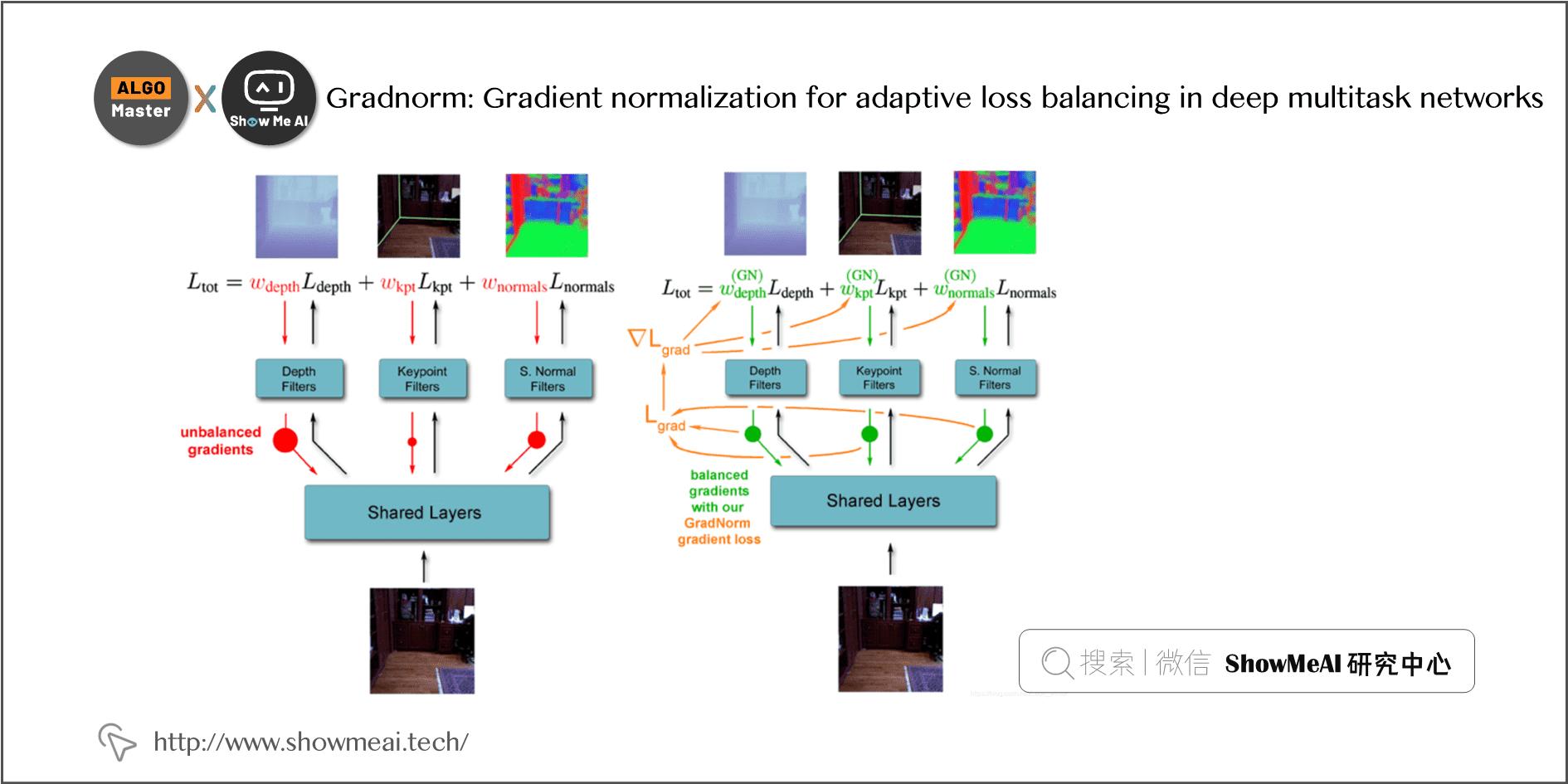
《Gradnorm: Gradient normalization for adaptive loss balancing in deep multitask networks》这篇paper尝试将不同任务的梯度调节到相似的量级来控制多任务网络的训练，以鼓励网络以尽可能相同的速度学习所有任务。

Gradient normalization具体实现方式如下：

• 定义两种类型的 \(Loss\) ：\(Label \quad Loss\) 和 \(Gradient \quad Loss\)。这两种 \(Loss\) 独立优化，不进行运算。
  • \(W4\) 的函数。
  • \(w_i(t)\) 的好坏，Gradient Loss 是关于权重 \(w_i(t)\) 的函数。
• \(w_i(t)\) 是一个变量（注意这里 \(w\) 与网络参数 \(W\) 是不同的），\(w\) 也通过梯度下降进行更新，\(t\) 表示当前处于网络训练的第 \(t\) 步。

gradnorm在单个batch step的流程总结如下：

1. 前向传播计算总损失 \(operatorname{Loss}=\Sigma_{i} w_{i} l_{i}\)
2. 计算 \(G_{W}^{i}(t), r_{i}(t), \bar{G}_{W}^{i}(t)\)
3. 计算 \(Grad \quad Loss\)
4. 计算 \(Grad \quad Loss\) 对 \(w_{i}\) 的导数
5. 利用第1步计算的 \(Loss\) 反向传播更新神经网络参数
6. 利用第4步的倒数更新 \(w_{i}\) (更新后在下一个 batch step 生效)
7. 对 \(w_{i}\) 进行 renormalize (下一个batch step使用的是 renormalize 之后的 \(w_{i}\) )

GradNorm核心代码参考：

class GradNorm:
    def __init__(self,
                 device,
                 model,
                 model_manager,
                 task_ids,
                 losses,
                 metrics,
                 train_loaders,
                 test_loaders,
                 tensorboard_writer,
                 optimizers,
                 alpha=1.):
​
        super().__init__(
                device, model, model_manager, task_ids, losses, metrics,
                train_loaders, test_loaders, tensorboard_writer)
​
        self.coeffs = torch.ones(
                len(task_ids), requires_grad=True, device=device)
        optimizer_def = getattr(optim, optimizers['method'])
        self.model_optimizer = optimizer_def(
                model.parameters(), **optimizers['kwargs'])
        self.grad_optimizer = optimizer_def(
                [self.coeffs], **optimizers['kwargs'])
​
        self.has_loss_zero = False
        self.loss_zero = torch.empty(len(task_ids), device=device)
        self.alpha = torch.tensor(alpha, device=device)
​
    def train_epoch(self):
        """
        训练1轮
        """
        self.model.train()
        loader_iterators = dict([(k, iter(v))
                                 for k, v in self.train_loaders.items()])
        train_losses_ts = dict(
                [(k, torch.tensor(0.).to(self.device)) for k in self.task_ids])
        train_metrics_ts = dict(
                [(k, torch.tensor(0.).to(self.device)) for k in self.task_ids])
        total_batches = min([len(loader)
                             for _, loader in self.train_loaders.items()])
        num_tasks = torch.tensor(len(self.task_ids)).to(self.device)
​
        relative_inverse = torch.empty(
                len(self.task_ids), device=self.device)
        _, all_branching_ids = self.model.execution_plan(self.task_ids)
        grad_norm = dict([
                (k, torch.zeros(len(self.task_ids), device=self.device))
                for k in all_branching_ids])
​
        pbar = tqdm(desc='  train', total=total_batches, ascii=True)
        for batch_idx in range(total_batches):
            tmp_coeffs = self.coeffs.clone().detach()
            self.model.zero_grad()
            self.grad_optimizer.zero_grad()
            for k, v in self.model.rep_tensors.items():
                if v.grad is not None:
                    v.grad.zero_()
                if v is not None:
                    v.detach()
​
            # 对每个task, 计算梯度，反向传播, 累计gradients norms
            for task_idx, task_id in enumerate(self.task_ids):
                data, target = loader_iterators[task_id].next()
                data, target = data.to(self.device), target.to(self.device)
​
                # do inference and accumulate losses
                output = self.model(data, task_id, retain_tensors=True)
                for index in all_branching_ids:
                    self.model.rep_tensors[index].retain_grad()
                loss = self.losses[task_id](output, target)
                weighted_loss = tmp_coeffs[task_idx] * loss
​
                weighted_loss.backward(retain_graph=False, create_graph=True)
                output.detach()
​
                # GradNorm relative inverse training rate accumulation
                if not self.has_loss_zero:
                    self.loss_zero[task_idx] = loss.clone().detach()
                relative_inverse[task_idx] = loss.clone().detach()
​
                # GradNorm accumulate gradients
                for index in all_branching_ids:
                    grad = self.model.rep_tensors[index].grad
                    grad_norm[index][task_idx] = torch.sqrt(
                            torch.sum(torch.pow(grad, 2)))
​
                # calculate training metrics
                with torch.no_grad():
                    train_losses_ts[task_id] += loss.sum()
                    train_metrics_ts[task_id] += \
                        self.metrics[task_id](output, target)
​
            # GradNorm calculate relative inverse and avg gradients norm
            self.has_loss_zero = True
            relative_inverse = relative_inverse / self.loss_zero.clone().detach()
            relative_inverse = relative_inverse / torch.mean(relative_inverse).clone().detach()
            relative_inverse = torch.pow(relative_inverse, self.alpha.clone().detach())
​
            coeff_loss = torch.tensor(0., device=self.device)
            for k, rep_grads in grad_norm.items():
                mean_norm = torch.mean(rep_grads)
                target = relative_inverse * mean_norm
                coeff_loss = coeff_loss + mean_norm.mean()
​
            # GradNorm optimize coefficients
            coeff_loss.backward()
​
            # optimize the model
            self.model_optimizer.step()
​
            pbar.update()
​
        for task_id in self.task_ids:
            train_losses_ts[task_id] /= \
                len(self.train_loaders[task_id].dataset)
            train_metrics_ts[task_id] /= \
                len(self.train_loaders[task_id].dataset)
​
        train_losses = dict([(k, v.item())
                             for k, v in train_losses_ts.items()])
        train_metrics = dict([(k, v.item())
                             for k, v in train_metrics_ts.items()])
        pbar.close()
        return train_losses, train_metrics
​

3）DWA [6]

《End-to-End Multi-Task Learning with Attention》这篇paper中直接定义了一个指标来衡量任务学习的快慢，然后来指导调节任务的权重。

用这一轮 \(Loss\) 除以上一轮 \(Loss\) ，这样可以得到这个任务 \(Loss\) 的下降情况用来衡量任务的学习速度，然后直接进行归一化得到任务的权重。当一个任务 \(Loss\) 比其他任务下降的慢时，这个任务的权重就会增加，下降的快时权重就会减小。是只考虑了任务下降速度的简化版的 Gradient normalization，简单直接。

4）PCGrad [7]

PCGrad 是 Google 在 NIPS 2020《Gradient surgery for multi-task learning》这篇 paper 里提出的方法，PCGrad 指出 MTL 多目标优化存在3个问题：

① 方向不一致，导致撕扯，需要解决
② 量级不一致，导致大 gradients 主导，需要解决
③ 大曲率，导致容易过拟合，需要解决

解决办法如下：

• 先检测不同任务的梯度是否冲突，冲突的标准就是是否有 negative similarity；
• 如果有冲突，就把冲突的分量 clip 掉（即，把其中一个任务的梯度投影到另一个任务梯度的正交方向上）。

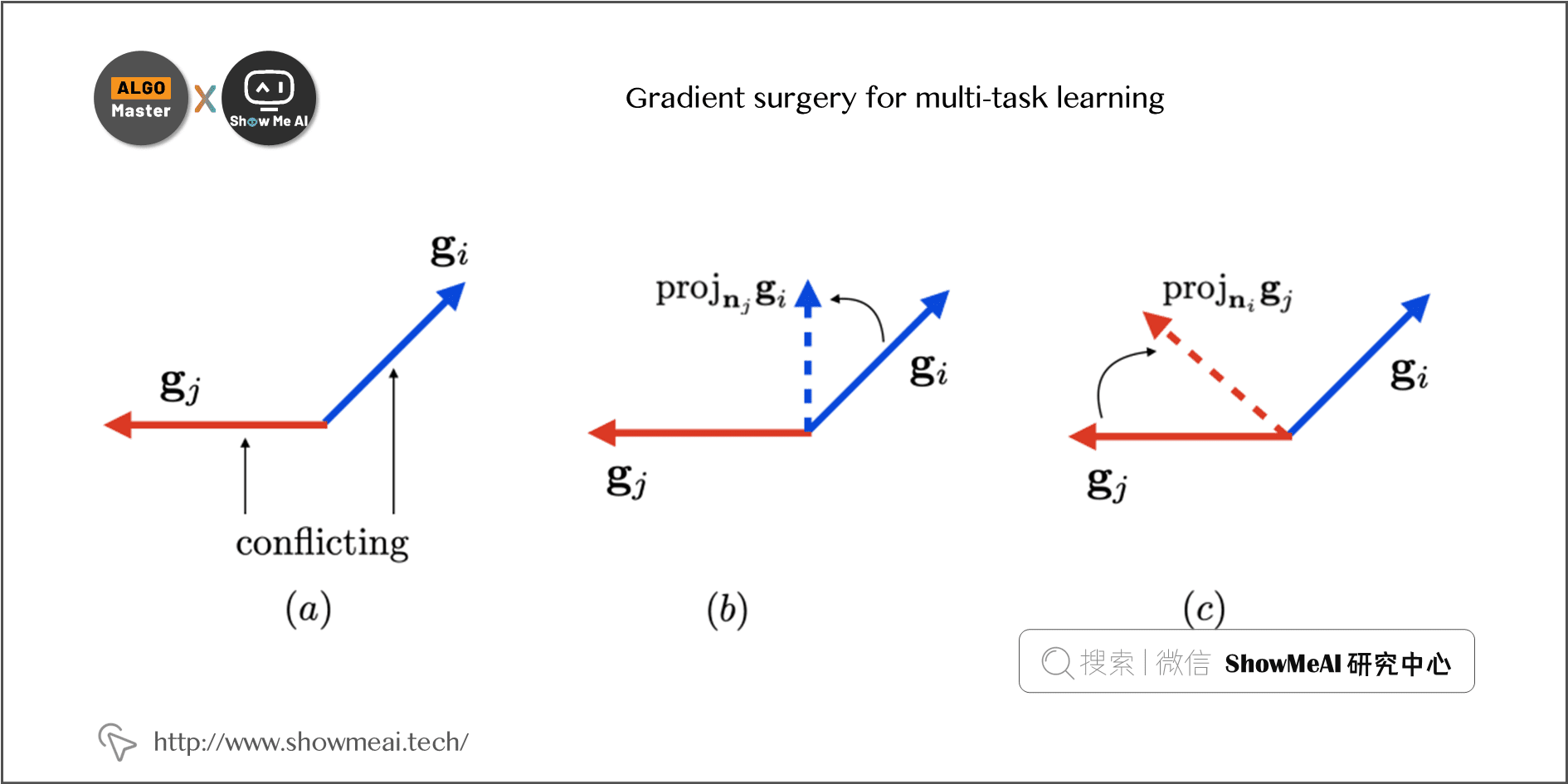
论文中的算法步骤如下：

PCGrad核心代码参考：

class PCGrad(optimizer.Optimizer):
​
    def __init__(self, optimizer, use_locking=False, name="PCGrad"):
        """
        optimizer优化器
        """
        super(PCGrad, self).__init__(use_locking, name)
        self.optimizer = optimizer
​
    def compute_gradients(self, loss, var_list=None,
                        gate_gradients=GATE_OP,
                        aggregation_method=None,
                        colocate_gradients_with_ops=False,
                        grad_loss=None):
        assert type(loss) is list
        num_tasks = len(loss)
        loss = tf.stack(loss)
        tf.random.shuffle(loss)
​
        # 计算每个任务的梯度
        grads_task = tf.vectorized_map(lambda x: tf.concat([tf.reshape(grad, [-1,]) 
                            for grad in tf.gradients(x, var_list) 
                            if grad is not None], axis=0), loss)
​
        # 计算梯度投影
        def proj_grad(grad_task):
            for k in range(num_tasks):
                inner_product = tf.reduce_sum(grad_task*grads_task[k])
                proj_direction = inner_product / tf.reduce_sum(grads_task[k]*grads_task[k])
                grad_task = grad_task - tf.minimum(proj_direction, 0.) * grads_task[k]
            return grad_task
​
        proj_grads_flatten = tf.vectorized_map(proj_grad, grads_task)
​
        # 把展平的投影梯度恢复原始shape
        proj_grads = []
        for j in range(num_tasks):
            start_idx = 0
            for idx, var in enumerate(var_list):
                grad_shape = var.get_shape()
                flatten_dim = np.prod([grad_shape.dims[i].value for i in range(len(grad_shape.dims))])
                proj_grad = proj_grads_flatten[j][start_idx:start_idx+flatten_dim]
                proj_grad = tf.reshape(proj_grad, grad_shape)
                if len(proj_grads) < len(var_list):
                    proj_grads.append(proj_grad)
                else:
                    proj_grads[idx] += proj_grad               
                start_idx += flatten_dim
        grads_and_vars = list(zip(proj_grads, var_list))
        return grads_and_vars

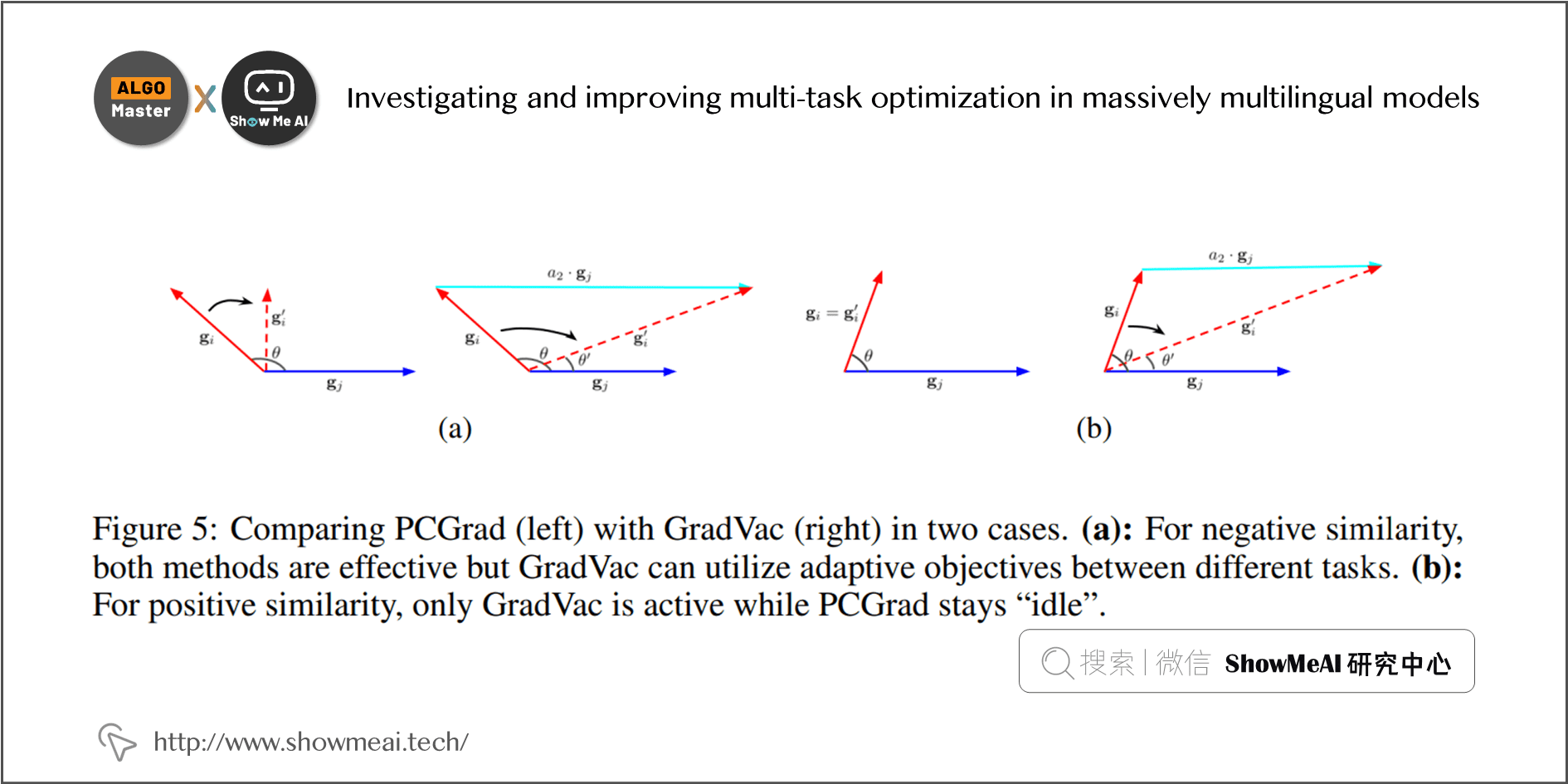
5）GradVac [8]

GradVac是Google在ICLR 2021《Investigating and improving multi-task optimization in massively multilingual models》这篇paper里提出的方法，作为PCGrad的改进应用在多语种机器翻译任务上。

对比PCGrad，我们看看GradVac的做法：

• PCGrad 只是设置了一个下界。让两个任务的 cosine 相似度至少是大于等于 \(0\) 的，不能出现负数。这个下界非常容易达到。
• 两个任务的真实相似度，其实是会逐渐收敛到一个水位。这个值可以认为是两个任务的真实相似度。
• 两个任务的 Gradinet 相似度，应当去靠近这个相似度，而不是只满足 PCGrad 设置的下界。

六、总结

总结一下，本文提到了多目标多任务场景下的优化方法，主要包含 网络结构优化 和 优化方法和策略提升两方面，最终目标都是希望缓解任务间的冲突和内耗，尽量优化提升所有业务目标。要构建一个 promising 的共赢多任务多目标解决方案，一些经验 tips 如下：

• 1）首先关注业务场景，思考业务目标优化重点，进而确定多任务的组合形式：
  • 主任务 + 主任务：解决业务场景既要又要的诉求，多个任务都希望提升
  • 主任务 + 辅任务：辅助任务为主任务提供一些知识信息的增强，帮助主任务提升 2.考虑不同任务间的重要度和相似性，考虑清楚辅助任务和主任务的关系；
• 2）实际训练过程中，可以训练优化其中1个任务，观察其他任务的 \(Loss\) 变化。
  • 其他任务 \(Loss\) 同步下降，则关联性较强
  • 其他任务 \(Loss\) 抖动或有上升趋势，要回到业务本身思考是否要联合多任务训练
• 3）网络结构选择 MMoE 或者 PLE。
• 4）训练过程中关注 \(Loss\) 的量级，如果不同任务之间差异很大，注意约束和控制。
• 5）训练过程的优化策略，可以尝试 PCGrad 等方法对梯度进行调整，并观察效果。

参考文献

• [1] Ma J, Zhao Z, Yi X, et al. Modeling task relationships in multi-task learning with multi-gate mixture-of-experts[C]//Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 2018: 1930-1939.
• [2] Jiaqi Ma, Zhe Zhao, Jilin Chen,et al. SNR: Sub-Network Routing forFlexible Parameter Sharing in Multi-Task Learning[C]//The Thirty-Third AAAI Conference on Artificial Intelligence (AAAI-19).2019: 216-223
• [3] Tang H, Liu J, Zhao M, et al. Progressive layered extraction (ple): A novel multi-task learning (mtl) model for personalized recommendations[C]//Fourteenth ACM Conference on Recommender Systems. 2020: 269-278.
• [4] Kendall A, Gal Y, Cipolla R. Multi-task learning using uncertainty to weigh losses for scene geometry and semantics[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2018: 7482-7491.
• [5] Chen Z, Badrinarayanan V, Lee C Y, et al. Gradnorm: Gradient normalization for adaptive loss balancing in deep multitask networks[C]//International Conference on Machine Learning. PMLR, 2018: 794-803.
• [6] Liu S, Johns E, Davison A J. End-to-end multi-task learning with attention[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2019: 1871-1880.
• [7] Yu T, Kumar S, Gupta A, et al. Gradient surgery for multi-task learning[J]. arXiv preprint arXiv:2001.06782, 2020.
• [8] Wang Z, Tsvetkov Y, Firat O, et al. Gradient vaccine: Investigating and improving multi-task optimization in massively multilingual models[J]. arXiv preprint arXiv:2010.05874, 2020.

---

ShowMeAI 大厂技术实现方案推荐

• 大厂解决方案系列 | 数据集&代码集（持续更新中）：https://www.showmeai.tech/tutorials/50
• ShowMeAI官方GitHub（实现代码）：https://github.com/ShowMeAI-Hub/
• 『推荐与广告』大厂解决方案
  • 大厂技术实现 | 多目标优化及应用（含代码实现）@推荐与广告计算系列
  • 大厂技术实现 | 爱奇艺短视频推荐业务中的多目标优化实践@推荐与计算广告系列
  • 大厂技术实现 | 腾讯信息流推荐排序中的并联双塔CTR结构@推荐与计算广告系列
• 『计算机视觉 CV』大厂解决方案
  • 大厂技术实现 | 图像检索及其在淘宝的应用@计算机视觉系列
  • 大厂技术实现 | 图像检索及其在高德的应用@计算机视觉系列
• 『自然语言处理 NLP』大厂解决方案
  • 大厂技术实现 | 详解知识图谱的构建全流程@自然语言处理系列
  • 大厂技术实现 | 爱奇艺文娱知识图谱的构建与应用实践@自然语言处理系列
• 『金融科技』大厂解决方案
• 『生物医疗』大厂解决方案
• 『智能制造』大厂解决方案
• 『其他AI垂直领域』大厂解决方案

ShowMeAI系列教程精选推荐

• 图解Python编程：从入门到精通系列教程
• 图解数据分析：从入门到精通系列教程
• 图解AI数学基础：从入门到精通系列教程
• 图解机器学习算法：从入门到精通系列教程
• 机器学习实战：手把手教你玩转机器学习系列
• 深度学习教程：吴恩达专项课程 · 全套笔记解读
• 自然语言处理教程：斯坦福CS224n课程 · 课程带学与全套笔记解读
• 深度学习与计算机视觉教程：斯坦福CS231n · 全套笔记解读