哈夫曼树

一.计算机编码

   计算机编码有很多方式，比如我们非常熟悉的ASCII码，它将每个字符编码成同样长度的码值（一个字节），但是实际上每个字符，出现的频率是不一样的，比方说e出现的频率要大于很多字符的频率，如果能将这些常见字符的编码缩短，而不太常见的字符编码可以适当增长，那么显然有助于优化存储空间。

二.判定树的优化

  下面这颗判定树可以将百分制成绩转化为五分制，不及格成绩只需要判定一步，90分需要4步，但是一个班的成绩通常是正态分布的，如果使用这棵树来判定成绩那么大部分人至少需要3-4步判断。

   那么如何根据结点不同的查找频率优化搜索树呢？

   假设每个叶子节点的查找频率是Wi，从根节点到叶节点的长度为Li，则带权路径的长度之和（WPL）为∑WiLi，现在我们的目标转化为使这个带权路径之和最小。目前我们直观的感受是使权值越高的节点离根节点越近。哈夫曼树就是用来解决这个问题的。

三.哈夫曼树的构造

 首先，将权值从小到大进行排序，把权值最小的两个结点并在一起，形成一棵新的二叉树。这个二叉树的权值就是并在一起两个权值的和。

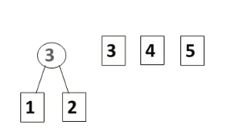
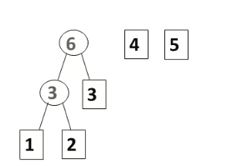
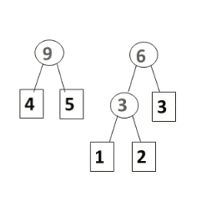
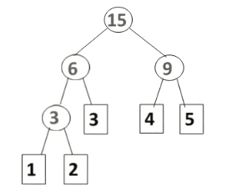
　如上图，哈夫曼树构造就是每次将两棵最小的树合并，形成一棵新的二叉树，然后这个二叉树权值就等于原来两棵权值之和，如此迭代下去。

    当然可以每次排序后选择两个权值最小的节点，但是更高效的方式是使用最小堆。

 

 代码注释很清晰，首先根据传入的数据建堆，然后在循环中每次删除两个最小元素，将这两个元素作为新树的左右儿子，最后将新树插入堆里。循环n次结束后，堆顶元素显然就是合并完成的树根了。总的时间复杂度为O(nlogn)。

 

 

参考：

   网易云课堂数据结构 http://mooc.study.163.com/course/1000033001#/info

   百度百科 https://baike.baidu.com/item/%E5%93%88%E5%A4%AB%E6%9B%BC%E6%A0%91/2305769?fr=aladdin